- Research Article
- Open access
- Published:
Analysis and Numerical Solutions of Positive and Dead Core Solutions of Singular Sturm-Liouville Problems
Advances in Difference Equations volume 2010, Article number: 969536 (2010)
Abstract
In this paper, we investigate the singular Sturm-Liouville problem  ,
,  ,
,  , where
, where  is a nonnegative parameter,
is a nonnegative parameter,  ,
,  , and
, and  . We discuss the existence of multiple positive solutions and show that for certain values of
. We discuss the existence of multiple positive solutions and show that for certain values of  , there also exist solutions that vanish on a subinterval
, there also exist solutions that vanish on a subinterval  , the so-called dead core solutions. The theoretical findings are illustrated by computational experiments for
, the so-called dead core solutions. The theoretical findings are illustrated by computational experiments for  and for some model problems from the class of singular differential equations
and for some model problems from the class of singular differential equations  discussed in Agarwal et al. (2007). For the numerical simulation, the collocation method implemented in our MATLAB code bvpsuite has been applied.
discussed in Agarwal et al. (2007). For the numerical simulation, the collocation method implemented in our MATLAB code bvpsuite has been applied.
1. Introduction
In the theory of diffusion and reaction (see, e.g., [1]), the reaction-diffusion phenomena are described by the equation

where  . Here
. Here  is the concentration of one of the reactants and
is the concentration of one of the reactants and  is the Thiele modulus. In case that
is the Thiele modulus. In case that  is radial symmetric with respect to
is radial symmetric with respect to  , the radial solutions of the above equation satisfying the boundary conditions
, the radial solutions of the above equation satisfying the boundary conditions

are solutions to a boundary value problem of the type

where  denotes the radial coordinate. Baxley and Gersdorff [2] discussed problem (1.3), where
denotes the radial coordinate. Baxley and Gersdorff [2] discussed problem (1.3), where  and
and  were continuous and
were continuous and  was allowed to be unbounded for
was allowed to be unbounded for  . They proved the existence of positive solutions and dead core solutions (vanishing on a subinterval
. They proved the existence of positive solutions and dead core solutions (vanishing on a subinterval  ,
,  ) of problem (1.3), and also covered the case of the function
) of problem (1.3), and also covered the case of the function  approximated by some regular function
approximated by some regular function  .
.
Problem (1.3) was a motivation for discussing positive, pseudo dead core, and dead core solutions to the singular boundary value problem with a  -Laplacian,
-Laplacian,


see [3]. Here  is a parameter, the function
is a parameter, the function  is non-negative and satisfies the Carathéodory conditions on
is non-negative and satisfies the Carathéodory conditions on  ,
,  for a.e.
for a.e.  , and
, and  is positive and satisfies the Carathéodory conditions on
is positive and satisfies the Carathéodory conditions on  ,
,  . Moreover, the function
. Moreover, the function  is singular at
is singular at  and
and  is singular at
is singular at  .
.
Let us denote by  the set of functions
the set of functions  which are absolutely continuous on
which are absolutely continuous on  for arbitrary small
for arbitrary small  .
.
A function  is called a positive solution of problem (1.4a)-(1.4b) if
is called a positive solution of problem (1.4a)-(1.4b) if  on
on  ,
,  ,
,  satisfies (1.4b) and (1.4a) holds for a.e.
satisfies (1.4b) and (1.4a) holds for a.e.  . We say that
. We say that  satisfying (1.4b) is a dead core solution of problem (1.4a)-(1.4b) if there exists a point
satisfying (1.4b) is a dead core solution of problem (1.4a)-(1.4b) if there exists a point  such that
such that  on
on  ,
,  on
on  ,
,  and (1.4a) holds for a.e.
and (1.4a) holds for a.e.  . The interval
. The interval  is called the dead core of
is called the dead core of . If
. If  ,
,  on
on  ,
,  ,
,  satisfies (1.4b) and (1.4a) holds a.e. on
satisfies (1.4b) and (1.4a) holds a.e. on  , then
, then  is called a pseudo dead core solution of problem (1.4a)-(1.4b).
is called a pseudo dead core solution of problem (1.4a)-(1.4b).
Since problem (1.4a)-(1.4b) is singular, the existence results in [3] are proved by a combination of the method of lower and upper functions with regularization and sequential techniques. Therefore, the notion of a sequential solution of problem (1.4a)-(1.4b) was introduced. In [3], conditions on the functions  , and
, and  were specified which guarantee that for each
were specified which guarantee that for each  , problem (1.4a)-(1.4b) has a sequential solution and that any sequential solution is either a positive solution, a pseudo dead core solution, or a dead core solution. Also, it was shown that all sequential solutions of (1.4a)-(1.4b) are positive solutions for sufficiently small positive values of
, problem (1.4a)-(1.4b) has a sequential solution and that any sequential solution is either a positive solution, a pseudo dead core solution, or a dead core solution. Also, it was shown that all sequential solutions of (1.4a)-(1.4b) are positive solutions for sufficiently small positive values of  and dead core solutions for sufficiently large values of
and dead core solutions for sufficiently large values of  .
.
The differential equation (1.5a) of the following boundary value problem satisfies all conditions specified in [3]:


Here,  , and
, and  . We note that in papers [2, 3] no information on the number of positive and dead core solutions of the underlying problem is given.
. We note that in papers [2, 3] no information on the number of positive and dead core solutions of the underlying problem is given.
In this paper, we discuss the singular boundary value problem


where  is a non-negative parameter, and the function
is a non-negative parameter, and the function  becomes unbounded at
becomes unbounded at  . Problem (1.6a)-(1.6b) is the special case of problem (1.4a)-(1.4b).
. Problem (1.6a)-(1.6b) is the special case of problem (1.4a)-(1.4b).
A function  is a positive solution of problem (1.6a)-(1.6b) if
is a positive solution of problem (1.6a)-(1.6b) if  satisfies the boundary conditions (1.6b),
satisfies the boundary conditions (1.6b),  on
on  and (1.6a) holds for
and (1.6a) holds for  . A function
. A function  is called a dead core solution of problem (1.6a)-(1.6b) if there exists a point
is called a dead core solution of problem (1.6a)-(1.6b) if there exists a point  such that
such that  for
for  ,
,  ,
,  satisfies (1.6b) and (1.6a) holds for
satisfies (1.6b) and (1.6a) holds for  . The interval
. The interval  is called the dead core of
is called the dead core of . If
. If  , then
, then  is called a pseudo dead core solution of problem (1.6a)-(1.6b).
is called a pseudo dead core solution of problem (1.6a)-(1.6b).
The aim of this paper is twofold.
-
(1)
First of all, we analyze relations between the values of the parameter
 and the number and types of solutions to problem (1.6a)-(1.6b), provided that
and the number and types of solutions to problem (1.6a)-(1.6b), provided that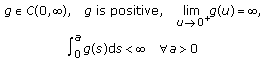 (1.7)
(1.7)or
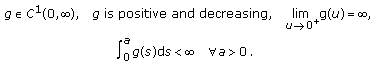 (1.8)
(1.8) -
(2)
Moreover, we compute solutions
 to the singular boundary value problem
to the singular boundary value problem 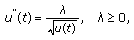 (1.9a)
(1.9a)

and the singular problem (1.5a), (1.9b). Note that (1.9a) is the special case of (1.6a) with  satisfying (1.8).
satisfying (1.8).
In [4] similar questions in context of (1.6a) and the Dirichlet boundary conditions  ,
,  have been discussed. For further results on existence of positive and dead core solutions to differential equations of the types
have been discussed. For further results on existence of positive and dead core solutions to differential equations of the types  and
and  , we refer the reader to [5–9]. The Dirichlet conditions have been discussed in [5–7, 9], while [8] deals with the Robin conditions
, we refer the reader to [5–9]. The Dirichlet conditions have been discussed in [5–7, 9], while [8] deals with the Robin conditions  ,
,  ,
,  ,
,  .
.
We now recapitulate the main analytical results formulated in Theorems 2.10, 2.12, and 2.13. First, we introduce the auxiliary function

where  satisfies (1.7). By Lemma 2.2, the equation
satisfies (1.7). By Lemma 2.2, the equation  has a unique continuous solution
has a unique continuous solution  , and the function
, and the function

is continuous on  . Let
. Let  . Then the following statements hold.
. Then the following statements hold.
-
(i)
Problem (1.6a)-(1.6b) has a positive solution if and only if

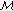 . In addition, for each
. In addition, for each  , problem (1.6a)-(1.6b) with
, problem (1.6a)-(1.6b) with 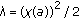 has a unique positive solution such that
has a unique positive solution such that  ,
,  .
. -
(ii)
Problem (1.6a)-(1.6b) has a pseudo dead core solution if and only if
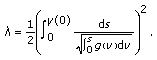 (1.12)
(1.12)This solution is unique.
-
(iii)
Problem (1.6a)-(1.6b) has a dead core solution if and only if
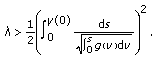 (1.13)
(1.13)
In addition, for all such  , problem (1.6a)-(1.6b) has a unique dead core solution.
, problem (1.6a)-(1.6b) has a unique dead core solution.
The final result concerning the multiplicity of positive solutions to problem (1.6a)-(1.6b) is given in Theorem 2.11. Let (1.8) hold and let 
 . Then
. Then  and for each
and for each  , there exist multiple positive solutions of problem (1.6a)-(1.6b).
, there exist multiple positive solutions of problem (1.6a)-(1.6b).
In Section 2 analytical results are presented. Here, we formulate the existence and uniqueness results for the solutions of the boundary value problem (1.6a)-(1.6b) and study the dependance of the solution on the parameter values  . The numerical treatment of problems (1.9a)-(1.9b) and (1.5a)-(1.5b) based on the collocation method is discussed in Section 3, where for different values of
. The numerical treatment of problems (1.9a)-(1.9b) and (1.5a)-(1.5b) based on the collocation method is discussed in Section 3, where for different values of  , we study positive, pseudo dead core, and dead core solutions of problem (1.9a)-(1.9b) and positive solutions of problem (1.5a)-(1.5b).
, we study positive, pseudo dead core, and dead core solutions of problem (1.9a)-(1.9b) and positive solutions of problem (1.5a)-(1.5b).
2. Analytical Results
2.1. Auxiliary Functions
Let assumption (1.7) hold, and let us introduce auxiliary functions  , and
, and  as
as

where  ,
,


Here, the positive constants  and
and  are identical with those used in boundary conditions (1.6b). Note that the function
are identical with those used in boundary conditions (1.6b). Note that the function  is used in the analysis of positive and pseudo dead core solutions of problem (1.6a)-(1.6b), while the function
is used in the analysis of positive and pseudo dead core solutions of problem (1.6a)-(1.6b), while the function  for its dead core solutions.
for its dead core solutions.
Properties of  are described in the following lemma.
are described in the following lemma.
Lemma 2.1.
Let assumption (1.7) hold and let  . Then
. Then  , and
, and  is increasing on
is increasing on  .
.
Proof.
Let  be arbitrary,
be arbitrary,  . Then
. Then  , and
, and  is increasing on
is increasing on  by [4, Lemma
by [4, Lemma  (where
(where  is replaced by
is replaced by  )]. Since
)]. Since  is arbitrary, the result immediately follows.
is arbitrary, the result immediately follows.
In the following lemma, we introduce functions  and
and  and discuss their properties.
and discuss their properties.
Lemma 2.2.
Let assumption (1.7) hold. Then the following statements follow.
(i)The function  is continuous on
is continuous on  , and
, and  for
for  .
.
(ii)For each  , there exists a unique
, there exists a unique  such that
such that

and  ,
,  for
for  ,
,  .
.
(iii)The function

is continuous on  .
.
Proof.
-
(i)
Let us define
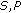 on
on 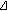 by
by 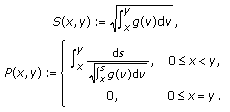 (2.6)
(2.6)
Then  . Let
. Let  and define
and define  . Then, by (1.7),
. Then, by (1.7),  . Hence
. Hence

and consequently  , which means that
, which means that  is continuous at
is continuous at  . Let
. Let  . We now show that
. We now show that  is continuous at the point
is continuous at the point  . Let us choose an arbitrary
. Let us choose an arbitrary  in the interval
in the interval  . Then
. Then  for
for  and
and  , where
, where

Since  by [4, Lemma
by [4, Lemma  (where 1 was replaced by
(where 1 was replaced by  )], it follows that
)], it follows that  is continuous at
is continuous at  . The continuity of
. The continuity of  at
at  now follows from the fact that
now follows from the fact that  is continuous at this point. Hence
is continuous at this point. Hence  is continuous on
is continuous on  , and from
, and from  we conclude
we conclude  . Since
. Since

we have  for
for  .
.
-
(ii)
Consider the equation
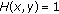 , that is,
, that is, 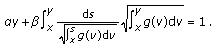 (2.10)
(2.10)
The function  is increasing on
is increasing on  ,
,  , and, for
, and, for  ,
,  . Hence, for each
. Hence, for each  , there exists a unique
, there exists a unique  such that
such that  and
and  . Clearly,
. Clearly,  for
for  . In order to prove that
. In order to prove that  , suppose the contrary, that is, suppose that
, suppose the contrary, that is, suppose that  is discontinuous at a point
is discontinuous at a point  ,
,  . Then there exist sequences
. Then there exist sequences  in
in  such that
such that  , and the sequences
, and the sequences  are convergent,
are convergent,  ,
,  ,
,  . Let
. Let  in
in  and in
and in  . This means
. This means  ,
,  , and
, and  by the definition of the function
by the definition of the function  , which contradicts
, which contradicts  .
.
-
(iii)
By (ii),
 (2.11)
(2.11)
 and
and  for
for  . Hence, the function
. Hence, the function  is continuous on
is continuous on  and positive on
and positive on  . From
. From

we now deduce that  . Since
. Since

where  , and
, and  on
on  ,
,  , we conclude
, we conclude  . Hence
. Hence  is continuous at
is continuous at  , and consequently
, and consequently  .
.
Let  be the function from Lemma 2.2(ii) defined on the interval
be the function from Lemma 2.2(ii) defined on the interval  . From now on,
. From now on,  denotes the value of
denotes the value of  at
at  , that is,
, that is,

In the following lemma, we prove a property of  which is crucial for discussing multiple positive solutions of problem (1.6a)-(1.6b).
which is crucial for discussing multiple positive solutions of problem (1.6a)-(1.6b).
Lemma 2.3.
Let assumption (1.8) hold and let the function  be given by (2.5). Then there exists
be given by (2.5). Then there exists  such that
such that

Proof.
Note that  d
d . We deduce from [4, Lemma
. We deduce from [4, Lemma  (with 1 replaced by
(with 1 replaced by  )] that there exists an
)] that there exists an  such that
such that

If  for some
for some  , then (2.16) yields
, then (2.16) yields

Consequently, inequality (2.15) holds for such an  . If the statement of the lemma were false, then some
. If the statement of the lemma were false, then some  would exist such that
would exist such that  and
and

From the following equalities, compare (2.4),

and from  , we conclude that
, we conclude that

Finally, from

we have  , which contradicts (2.18).
, which contradicts (2.18).
In order to discuss dead core solutions of problem (1.6a)-(1.6b) and their dead cores, we need to introduce two additional functions  and
and  related to
related to  and study their properties.
and study their properties.
Lemma 2.4.
Assume that (1.7) holds and let  be given by (2.3). Then for each
be given by (2.3). Then for each  , there exists a unique
, there exists a unique  such that
such that

The function  is continuous and decreasing on
is continuous and decreasing on  , and the function
, and the function

is continuous and increasing on  . Moreover,
. Moreover,  .
.
Proof.
It follows from (1.7) that  . Also,
. Also,  is increasing w.r.t. both variables,
is increasing w.r.t. both variables,  for any
for any  , and
, and  ,
,  for any
for any  . Hence, for each
. Hence, for each  , there exists a unique
, there exists a unique  such that
such that  . In order to prove that
. In order to prove that  is decreasing on
is decreasing on  , assume on the contrary that
, assume on the contrary that  for some
for some  . Then
. Then  which contradicts
which contradicts  for
for  . Hence,
. Hence,  is decreasing on
is decreasing on  . If
. If  was discontinuous at a point
was discontinuous at a point  , then there would exist sequences
, then there would exist sequences  and
and  in
in  such that
such that  and
and  ,
,  are convergent,
are convergent,  , and
, and  with
with  . Taking the limits
. Taking the limits  in
in  and
and  , we obtain
, we obtain  ,
,  . Consequently,
. Consequently,  by the definition of the function
by the definition of the function  , which is not possible.
, which is not possible.
By (2.22),

and therefore,

It follows from the properties of  that the functions
that the functions  ,
,  are continuous, positive, and increasing on
are continuous, positive, and increasing on  . Hence (2.25) implies that
. Hence (2.25) implies that  and
and  is increasing. Moreover,
is increasing. Moreover,  since
since  d
d is bounded on
is bounded on  .
.
Corollary 2.5.
Let assumption (1.7) hold. Then

and for each  satisfying the inequality
satisfying the inequality

there exists a unique  such that
such that

Proof.
The equalities  for
for  and
and  imply that
imply that  . Since the function
. Since the function  defined by (2.23) is continuous and increasing on
defined by (2.23) is continuous and increasing on  , it follows that
, it follows that  for
for  ; see (2.26). Let us choose an arbitrary
; see (2.26). Let us choose an arbitrary  satisfying (2.27). Then
satisfying (2.27). Then  . Now, the properties of
. Now, the properties of  guarantee that equation
guarantee that equation  has a unique solution
has a unique solution  . This means that (2.28) holds for a unique
. This means that (2.28) holds for a unique  .
.
2.2. Dependence of Solutions on the Parameter 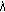
The following two lemmas characterize the dependence of positive and dead core solutions of problem (1.6a)-(1.6b) on the parameter  .
.
Lemma 2.6.
Let assumption (1.7) hold and let  be a positive solution of problem (1.6a)-(1.6b) for some
be a positive solution of problem (1.6a)-(1.6b) for some  . Also, let
. Also, let  , and
, and  . Then
. Then  ,
,  ,
,



where the function  is given by (2.2).
is given by (2.2).
Proof.
Since  and
and  for
for  , we conclude that
, we conclude that  on
on  and
and  ,
,  . By integrating the equality
. By integrating the equality  over
over  , we obtain
, we obtain

and consequently, since  on
on  ,
,

Finally, integrating

over  yields (2.30). Now we set
yields (2.30). Now we set  in (2.30) and obtain (2.29). Equality (2.31) follows from
in (2.30) and obtain (2.29). Equality (2.31) follows from  and from
and from

Remark 2.7.
Let (1.7) hold and let  be a pseudo dead core solution of problem (1.6a)-(1.6b). Then, by the definition of pseudo dead core solutions,
be a pseudo dead core solution of problem (1.6a)-(1.6b). Then, by the definition of pseudo dead core solutions,  . We can proceed analogously to the proof of Lemma 2.6 in order to show that
. We can proceed analogously to the proof of Lemma 2.6 in order to show that

where  , and
, and


From (2.38), we finally have  . Consequently,
. Consequently,  .
.
Remark 2.8.
If  , then
, then  ,
,  is the unique solution of problem (1.6a)-(1.6b). This solution is positive.
is the unique solution of problem (1.6a)-(1.6b). This solution is positive.
Lemma 2.9.
Let assumption (1.7) hold and let  be a dead core solution of problem (1.6a)-(1.6b) for some
be a dead core solution of problem (1.6a)-(1.6b) for some  . Moreover, let
. Moreover, let  . Then
. Then  and there exists a point
and there exists a point  such that
such that  for
for  ,
,



where the function  is given by (2.3). Furthermore,
is given by (2.3). Furthermore,  is the unique dead core solution of problem (1.6a)-(1.6b) with
is the unique dead core solution of problem (1.6a)-(1.6b) with  .
.
Proof.
Since  is a dead core solution of problem (1.6a)-(1.6b) with
is a dead core solution of problem (1.6a)-(1.6b) with  , there exists by definition, a point
, there exists by definition, a point  such that
such that  ,
,  for
for  and
and  on
on  . Consequently,
. Consequently,  on
on  , and
, and  . We can now proceed analogously to the proof of Lemma 2.6 to show that
. We can now proceed analogously to the proof of Lemma 2.6 to show that

and (2.39) holds. Setting  in (2.39), we obtain (2.40). Also, from (1.6b),
in (2.39), we obtain (2.40). Also, from (1.6b),  ,
,

equality (2.41) follows.
It remains to verify that  is the unique dead core solution of problem (1.6a)-(1.6b) with
is the unique dead core solution of problem (1.6a)-(1.6b) with  . Let us suppose that
. Let us suppose that  is another dead core solution of the above problem. Let
is another dead core solution of the above problem. Let  for
for  and
and  on
on  for some
for some  . Then
. Then  for
for  , and consequently
, and consequently  on
on  and
and  . Hence, compare (2.40) and (2.41),
. Hence, compare (2.40) and (2.41),


Since

by (2.41), and the function  is increasing and continuous on
is increasing and continuous on  , we deduce from (2.45) and (2.46) that
, we deduce from (2.45) and (2.46) that  . Then (2.40) and (2.44) yield
. Then (2.40) and (2.44) yield  . Therefore,
. Therefore,  d
d for
for  . Finally, since
. Finally, since  for
for  and since by Lemma 2.1 the function
and since by Lemma 2.1 the function  is increasing on
is increasing on  ,
,  follows. This completes the proof.
follows. This completes the proof.
2.3. Main Results
Let the function  be given by (2.5) and let us denote by
be given by (2.5) and let us denote by  the range of the function
the range of the function  restricted to the interval
restricted to the interval  ,
,

Since  by Lemma 2.2(iii),
by Lemma 2.2(iii),  for
for  and
and  , we can have either (i)
, we can have either (i)  for
for  , or (ii)
, or (ii)  for some
for some  . For (i), we have
. For (i), we have  , while in case of (ii),
, while in case of (ii),  with
with

holds. Clearly,  .
.
Positive solutions of problem (1.6a)-(1.6b) are analyzed in the following theorem.
Theorem 2.10.
Let assumption (1.7) hold. Then problem (1.6a)-(1.6b) has a positive solution if and only if 
 . Additionally, for each
. Additionally, for each  , problem (1.6a)-(1.6b) with
, problem (1.6a)-(1.6b) with  has a unique positive solution
has a unique positive solution  such that
such that  and
and  .
.
Proof.
Let  be a positive solution of problem (1.6a)-(1.6b) for
be a positive solution of problem (1.6a)-(1.6b) for  . By Lemma 2.6, (2.31) holds with
. By Lemma 2.6, (2.31) holds with  and
and  . Furthermore, by Lemmas 2.2(ii) and 2.6,
. Furthermore, by Lemmas 2.2(ii) and 2.6,  , which together with (2.29) implies that
, which together with (2.29) implies that  . Consequently,
. Consequently, 
 . For
. For  , problem (1.6a)-(1.6b) has the unique positive solution
, problem (1.6a)-(1.6b) has the unique positive solution  ; see Remark 2.8. Since
; see Remark 2.8. Since  ,
, 
 . Consequently, if problem (1.6a)-(1.6b) has a positive solution, then
. Consequently, if problem (1.6a)-(1.6b) has a positive solution, then 
 .
.
We now show that for each 
 , problem (1.6a)-(1.6b) has a positive solution, and if
, problem (1.6a)-(1.6b) has a positive solution, and if  for some
for some  , then problem (1.6a)-(1.6b) has a unique positive solution
, then problem (1.6a)-(1.6b) has a unique positive solution  such that
such that  and
and  . Let us choose
. Let us choose 
 . Then
. Then  for some
for some  . If
. If  , then
, then  . Consequently,
. Consequently,  and
and  is the unique solution of problem (1.6a)-(1.6b). Clearly,
is the unique solution of problem (1.6a)-(1.6b). Clearly,  and
and  since
since  . Let us suppose that
. Let us suppose that  . If
. If  is a positive solution of problem (1.6a)-(1.6b) and
is a positive solution of problem (1.6a)-(1.6b) and  , then, by Lemma 2.6; see (2.30), the equality
, then, by Lemma 2.6; see (2.30), the equality  holds for
holds for  , where
, where  is given by (2.1). Hence, in order to prove that for
is given by (2.1). Hence, in order to prove that for  problem (1.6a)-(1.6b) has a unique positive solution
problem (1.6a)-(1.6b) has a unique positive solution  such that
such that  and
and  , we have to show that the equation
, we have to show that the equation

has a unique solution  ; this solution is a positive solution of problem (1.6a)-(1.6b), and
; this solution is a positive solution of problem (1.6a)-(1.6b), and  ,
,  . Since
. Since  ,
,  is increasing by Lemma 2.1, and
is increasing by Lemma 2.1, and  , (2.49) has a unique solution
, (2.49) has a unique solution  . It follows from
. It follows from  and
and  that
that  and
and  . In addition,
. In addition,

Hence,  and
and  . In order to show that
. In order to show that  is continuous at
is continuous at  , we set
, we set  . Then, compare (2.49),
. Then, compare (2.49),

and therefore,

Consequently,  , and so
, and so  is continuous at
is continuous at  , or equivalently,
, or equivalently,  . Now (2.50) indicates that
. Now (2.50) indicates that  and
and

Moreover, by the de L'Hospital rule,

As a result  and
and  for
for  . Since
. Since  and, by (2.50),
and, by (2.50),  , we have
, we have

by Lemma 2.2(ii). Thus,  satisfies (1.6b), and therefore
satisfies (1.6b), and therefore  is a unique positive solution of problem (1.6a)-(1.6b) such that
is a unique positive solution of problem (1.6a)-(1.6b) such that  and
and  .
.
The following theorem deals with multiple positive solutions of problem (1.6a)-(1.6b).
Theorem 2.11.
Let assumption (1.8) hold. Then  , with
, with  given by (2.48), and for each
given by (2.48), and for each  , there exist multiple positive solutions of problem (1.6a)-(1.6b).
, there exist multiple positive solutions of problem (1.6a)-(1.6b).
Proof.
By Lemmas 2.2(iii) and 2.3,  ,
,  , and
, and  in a right neighbourhood of
in a right neighbourhood of  . Hence,
. Hence,  . Let us choose
. Let us choose  . Then there exist
. Then there exist  such that
such that  for
for  . Now Theorem 2.10 guarantees that problem (1.6a)-(1.6b) has positive solutions
. Now Theorem 2.10 guarantees that problem (1.6a)-(1.6b) has positive solutions  and
and  such that
such that  ,
,  . Since
. Since  , we have
, we have  and therefore, for each
and therefore, for each  , problem (1.6a)-(1.6b) has multiple positive solutions.
, problem (1.6a)-(1.6b) has multiple positive solutions.
Next, we present results for pseudo dead core solutions of problem (1.6a)-(1.6b). Note that here  .
.
Theorem 2.12.
Let assumption (1.7) hold. Then problem (1.6a)-(1.6b) has a pseudo dead core solution if and only if

Moreover, for  given by (2.56), problem (1.6a)-(1.6b) has a unique pseudo dead core solution such that
given by (2.56), problem (1.6a)-(1.6b) has a unique pseudo dead core solution such that  .
.
Proof.
Let us assume that  is a pseudo dead core solution of problem (1.6a)-(1.6b) and let
is a pseudo dead core solution of problem (1.6a)-(1.6b) and let  . Then, by Remark 2.7, equalities (2.36), (2.38) hold, and
. Then, by Remark 2.7, equalities (2.36), (2.38) hold, and  . Also, (2.37) implies that
. Also, (2.37) implies that  is a solution of the equation
is a solution of the equation

where  and
and  are given by (2.1) and (2.56), respectively. The result follows by showing that equation (2.57) has a unique solution and that this solution is a pseudo dead core solution of problem (1.6a)-(1.6b). We verify these facts for solutions of (2.57) arguing as in the proof of Theorem 2.10, with
are given by (2.1) and (2.56), respectively. The result follows by showing that equation (2.57) has a unique solution and that this solution is a pseudo dead core solution of problem (1.6a)-(1.6b). We verify these facts for solutions of (2.57) arguing as in the proof of Theorem 2.10, with  replaced by 0.
replaced by 0.
In the final theorem below, we deal with dead core solutions of problem (1.6a)-(1.6b).
Theorem 2.13.
Let assumption (1.7) hold and let  be the function defined in Lemma 2.4. Then the following statements hold.
be the function defined in Lemma 2.4. Then the following statements hold.
-
(i)
Problem (1.6a)-(1.6b) has a dead core solution if and only if
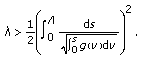 (2.58)
(2.58) -
(ii)
For each
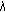 satisfying (2.58), problem (1.6a)-(1.6b) has a unique dead core solution.
satisfying (2.58), problem (1.6a)-(1.6b) has a unique dead core solution. -
(iii)
If the subinterval
 is the dead core of a dead core solution
is the dead core of a dead core solution  of problem (1.6a)-(1.6b), then
of problem (1.6a)-(1.6b), then 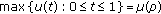 and
and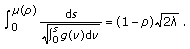 (2.59)
(2.59)
Proof.
-
(i)
Let
 be a dead core solution of problem (1.6a)-(1.6b) for some
be a dead core solution of problem (1.6a)-(1.6b) for some 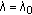 and let
and let  . Then there exists a point
. Then there exists a point 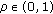 such that
such that 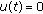 for
for  , and equalities (2.39), (2.40), and (2.41) are satisfied by Lemma 2.9. We deduce from (2.41) and from Lemma 2.4 that
, and equalities (2.39), (2.40), and (2.41) are satisfied by Lemma 2.9. We deduce from (2.41) and from Lemma 2.4 that 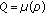 . Therefore, compare (2.40),
. Therefore, compare (2.40),  (2.60)
(2.60)
Since

by Corollary 2.5, we have

Hence, if problem (1.6a)-(1.6b) has a dead core solution, then  satisfies inequality (2.58).
satisfies inequality (2.58).
We now prove that for each  satisfying (2.58), problem (1.6a)-(1.6b) has a dead core solution. Let us choose
satisfying (2.58), problem (1.6a)-(1.6b) has a dead core solution. Let us choose  satisfying (2.58). Then, by Corollary 2.5, there exists a unique
satisfying (2.58). Then, by Corollary 2.5, there exists a unique  such that
such that

Let us now consider, compare (2.39),

where  is given by (2.1). Since
is given by (2.1). Since  and
and  is increasing on
is increasing on  by Lemma 2.1,
by Lemma 2.1,  , and, by (2.63),
, and, by (2.63),  , there exists a unique solution
, there exists a unique solution  of (2.64) and
of (2.64) and  ,
,  . In addition,
. In addition,

and consequently,  and
and  . Since
. Since

by the Mean Value Theorem for integrals, where  , we have
, we have

Therefore,

since  . Hence,
. Hence,  is continuous at
is continuous at  , and
, and  . Furthermore,
. Furthermore,

Let

Then  ,
,  for
for  ,
,  ,
,  , and
, and

Thus,

where  is given by (2.3). Since
is given by (2.3). Since  by Lemma 2.4,
by Lemma 2.4,  satisfies the boundary conditions (1.6b). Consequently,
satisfies the boundary conditions (1.6b). Consequently,  is a dead core solution of problem (1.6a)-(1.6b).
is a dead core solution of problem (1.6a)-(1.6b).
-
(ii)
Let us choose an arbitrary
 satisfying (2.58). By (i), problem (1.6a)-(1.6b) has a dead core solution which is unique by Lemma 2.9.
satisfying (2.58). By (i), problem (1.6a)-(1.6b) has a dead core solution which is unique by Lemma 2.9. -
(iii)
Let the subinterval
 be the dead core of a dead core solution
be the dead core of a dead core solution  of problem (1.6a)-(1.6b). Then, by Lemma 2.9, equalities (2.40) and (2.41) hold with
of problem (1.6a)-(1.6b). Then, by Lemma 2.9, equalities (2.40) and (2.41) hold with  replaced by
replaced by 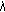 and
and  . Since
. Since  by the definition of the function
by the definition of the function  , we have
, we have 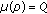 . Equality (2.59) now follows from (2.40) with
. Equality (2.59) now follows from (2.40) with 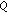 and
and  replaced by
replaced by 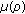 and
and 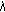 , respectively.
, respectively.
Example 2.14.
We now turn to the case study of the boundary value problem (1.9a)-(1.9b),

Note that (1.9a)-(1.9b) is a special case of (1.6a)-(1.6b) with  satisfying (1.8). Since
satisfying (1.8). Since

we have

for  , and
, and  for
for  . By Lemma 2.2, the equation
. By Lemma 2.2, the equation  has a unique solution
has a unique solution  for
for  ,
,  ,
,  for
for  , and
, and  . Let
. Let

Then  ,
,  , and
, and  . In order to show that
. In order to show that  is increasing on
is increasing on  it is sufficient to verify that
it is sufficient to verify that  is injective. Let us assume that this is not the case, then there exist
is injective. Let us assume that this is not the case, then there exist  ,
,  , such that
, such that  . From
. From  ,
,  , or equivalently, from
, or equivalently, from

it follows that  , and
, and  which is a contradiction. Hence,
which is a contradiction. Hence,  is increasing on
is increasing on  and therefore, there exists the inverse function
and therefore, there exists the inverse function  mapping
mapping  onto
onto  . Since
. Since

and  for
for  , we have
, we have

Consequently,

In order to discuss the range  of the function
of the function  and the value of
and the value of  for
for  , we first consider properties of the function
, we first consider properties of the function

defined on  . Let
. Let

Then

where  . The function
. The function  vanishes only at point
vanishes only at point

in the interval  , and
, and  , because
, because  and
and  . Since
. Since  ,
,  on
on  ,
,  on
on  and
and

for  , we have
, we have  on
on  and
and  on
on  . Let us define
. Let us define  . Then
. Then  , and it follows from
, and it follows from  that
that  on
on  and
and  on
on  . Consequently,
. Consequently,  is increasing on
is increasing on  and decreasing on
and decreasing on  . It follows from the equality
. It follows from the equality  for
for  and from the properties of the functions
and from the properties of the functions  and
and  that
that  is increasing on
is increasing on  and decreasing on
and decreasing on  . Hence,
. Hence,  , where
, where  . Also,
. Also,

Using properties of the function  and the results of Theorems 2.10–2.13, we can now characterize the structure of the solution
and the results of Theorems 2.10–2.13, we can now characterize the structure of the solution  .
.
-
(i)
For each
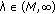 , there exists only a unique dead core solution of problem (1.9a)-(1.9b).
, there exists only a unique dead core solution of problem (1.9a)-(1.9b). -
(ii)
For
 , there exist a unique dead core solution and a unique positive solution of problem (1.9a)-(1.9b).
, there exist a unique dead core solution and a unique positive solution of problem (1.9a)-(1.9b). -
(iii)
For each
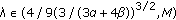 , there exist a unique dead core solution and exactly two positive solutions of problem (1.9a)-(1.9b).
, there exist a unique dead core solution and exactly two positive solutions of problem (1.9a)-(1.9b). -
(iv)
For
 , there exist the unique pseudo dead core solution
, there exist the unique pseudo dead core solution  and a unique positive solution of problem (1.9a)-(1.9b).
and a unique positive solution of problem (1.9a)-(1.9b). -
(v)
For each
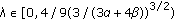 , there exist only a unique positive solution of problem (1.9a)-(1.9b).
, there exist only a unique positive solution of problem (1.9a)-(1.9b).
Using Theorem 2.10, Lemma 2.6, and the properties of the function  , we can specify further properties of positive solutions of problem (1.9a)-(1.9b).
, we can specify further properties of positive solutions of problem (1.9a)-(1.9b).
-
(i)
If
 is the (unique) positive solution of problem (1.9a)-(1.9b) with
is the (unique) positive solution of problem (1.9a)-(1.9b) with  , then
, then  , where
, where 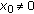 is the root of the equation
is the root of the equation 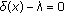 .
. -
(ii)
If
 are the (unique) positive solutions of problem (1.9a)-(1.9b) with
are the (unique) positive solutions of problem (1.9a)-(1.9b) with  , then
, then 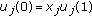 ,
, 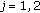 , where
, where 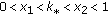 , are the roots of the equation
, are the roots of the equation 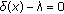 .
.
We are also able to give some more information on the dead core solutions of problem (1.9a)-(1.9b). Since

the function  ,
,  , is the solution of the equation
, is the solution of the equation  . Let us choose an arbitrary
. Let us choose an arbitrary  . By Corollary 2.5, the equation; see (2.28),
. By Corollary 2.5, the equation; see (2.28),

has a unique solution  . Consequently,
. Consequently,

One can easily show that the function

is the unique dead core solution of problem (1.9a)-(1.9b). Additionally, it follows from Theorem 2.13(iii) that  since
since  .
.
3. Numerical Treatment
We now aim at the numerical approximation to the solution of the following two-point boundary value problem:

For the numerical solution of (3.1), we are using the collocation method implemented in our Matlab code bvpsuite. It is a new version of the general purpose Matlab code sbvp, compare [10–12]. This code has already been used to treat a variety of problems relevant in application; see, for example, [13–17]. Collocation is a widely used and well-studied standard solution method for two-point boundary value problems, compare [18] and the references therein. It can also be successfully applied to boundary value problems with singularities.
In the scope of the code are systems of ordinary differential equations of arbitrary order. For simplicity of notation we present a problem of maximal order four which can be given in a fully implicit form,


In order to compute the numerical approximation, we first introduce a mesh

The approximation for  is a collocation function
is a collocation function

where we require  in case that the order of the underlying differential equation is
in case that the order of the underlying differential equation is  . Here,
. Here,  are polynomials of maximal degree
are polynomials of maximal degree  which satisfy the system (3.2a) at
which satisfy the system (3.2a) at  inner collocation points
inner collocation points

and the associated boundary conditions (3.2b).
Classical theory, compare [18], predicts that the convergence order for the global error of the method is at least  , where
, where  is the maximal stepsize,
is the maximal stepsize,  To increase efficiency, an adaptive mesh selection strategy based on an a posteriori estimate for the global error of the collocation solution is utilized. A more detailed description of the numerical approach can be found in [4].
To increase efficiency, an adaptive mesh selection strategy based on an a posteriori estimate for the global error of the collocation solution is utilized. A more detailed description of the numerical approach can be found in [4].
The code bvpsuite also allows to follow a path in the parameter-solution space. This means that in the following problem setting, parameter  is unknown:
is unknown:


where  is given. The path following strategy can also cope with turning points in the path. The theoretical justification for the path following strategy implemented in bvpsuite has been given in [19].
is given. The path following strategy can also cope with turning points in the path. The theoretical justification for the path following strategy implemented in bvpsuite has been given in [19].
We first study the boundary problem (1.9a)-(1.9b). Positive solutions of problem (1.5a)-(1.5b) will be discussed in Section 3.4.
The above analytical discussion indicates that depending on the values of  ,
,  ,
,  , the problem has one or more positive solutions, a pseudo dead core solution or a dead core solution. All numerical approximations have been calculated on a fixed mesh with
, the problem has one or more positive solutions, a pseudo dead core solution or a dead core solution. All numerical approximations have been calculated on a fixed mesh with  subintervals and collocation degree
subintervals and collocation degree  . Figure 1 shows
. Figure 1 shows  for our choice of parameters used in the following sections. Here,
for our choice of parameters used in the following sections. Here,  is given by (2.81).
is given by (2.81).
3.1. Positive Solutions
For  ),
),  , there exist a unique positive solution. This solution was found numerically by using the original problem formulation (1.9a)-(1.9b). For
, there exist a unique positive solution. This solution was found numerically by using the original problem formulation (1.9a)-(1.9b). For  we obtain
we obtain  . In Figure 2 we display the numerical solution, the error estimate and the residual for
. In Figure 2 we display the numerical solution, the error estimate and the residual for  . The residual
. The residual  is calculated by substituting the numerical solution
is calculated by substituting the numerical solution  into the differential equation,
into the differential equation,

Due to the very small size of the error estimate and residual, it is obvious that the numerical approximation is very accurate. According to the analytical results, a solution to the problem satisfies  where
where  is a root of
is a root of  . Here, we have
. Here, we have  and
and  which again shows the high quality of the numerical solution. In Figure 3 we depict the results for the parameter
which again shows the high quality of the numerical solution. In Figure 3 we depict the results for the parameter  ,
,  and
and  . For this choice of parameters
. For this choice of parameters  and
and  .
.
For  there exists a unique positive solution. To compute its numerical approximation, we rewrite the problem (1.9a)-(1.9b) and consider
there exists a unique positive solution. To compute its numerical approximation, we rewrite the problem (1.9a)-(1.9b) and consider

The numerical results related to parameter sets  ,
,  , and
, and  ,
,  are shown in Figure 4 and Figure 5, respectively.
are shown in Figure 4 and Figure 5, respectively.
Again, the error estimate and the residual are both very small and  , so
, so  . Moreover, for the second set of parameters,
. Moreover, for the second set of parameters,  and
and  .
.
For  with
with  there exist two positive solutions. These two different solutions for a fixed value of
there exist two positive solutions. These two different solutions for a fixed value of  can be characterized via the roots
can be characterized via the roots  of
of  for
for  . The choice of parameters remains the same. For
. The choice of parameters remains the same. For  ,
,  and
and  the solution corresponding to
the solution corresponding to  is shown in Figure 6. The solution corresponding to
is shown in Figure 6. The solution corresponding to  is depicted in Figure 7. Note that for these values of
is depicted in Figure 7. Note that for these values of  and
and  we have
we have  .
.
The first of those two solutions was found using the reformulated problem (3.8) with  as the right-hand side. For the second solution it was necessary to rewrite the problem again and use
as the right-hand side. For the second solution it was necessary to rewrite the problem again and use

with  as a free unknown parameter and
as a free unknown parameter and  as a necessary additional boundary condition. Here,
as a necessary additional boundary condition. Here,  and
and  . For comparison,
. For comparison,  and
and  . In Figures 8 and 9, two different positive solutions for the second parameter set,
. In Figures 8 and 9, two different positive solutions for the second parameter set,  ,
,  , and
, and  , are shown. Note that
, are shown. Note that  ,
,  and
and  . For this example
. For this example  and
and  . Here,
. Here,  and
and  . Finally, for
. Finally, for  , there exists a unique positive solution. In Figures 10 and 11 we display the numerical results for
, there exists a unique positive solution. In Figures 10 and 11 we display the numerical results for  ,
,  and for
and for  ,
,  , respectively. In this example,
, respectively. In this example,  and
and  . Using this latter set of parameters, we obtain
. Using this latter set of parameters, we obtain  and
and  . All positive solutions could be easily found and they all show a very satisfactory level of accuracy.
. All positive solutions could be easily found and they all show a very satisfactory level of accuracy.
3.2. Pseudo Dead Core Solutions
In order to calculate the pseudo dead core solutions, we solved the following problem:

where the differential equation has been premultiplied by the factor  . Otherwise, the problem formulated as (3.1) or (3.8), would have not been well defined at all points
. Otherwise, the problem formulated as (3.1) or (3.8), would have not been well defined at all points  such that
such that  . In Figures 12 and 13, we report on the pseudo dead core solutions for
. In Figures 12 and 13, we report on the pseudo dead core solutions for

In this case, the analytical unique pseudo dead core solution is known,

Therefore, the exact global error is accessible. In Table 1, we show the values for the global error,  where
where  is the numerical solution at
is the numerical solution at  .
.
3.3. Dead Core Solutions
We now deal with the dead core solutions of the problem. Note that they only occur for

Moreover, the relation between  and
and  , where
, where  is such that the solution vanishes on
is such that the solution vanishes on  , is given by
, is given by

Also, the dead core solution is known,

For the experiments, we used  and
and  , in order to solve the problem,
, in order to solve the problem,

Clearly, if we approached the problem (3.16) directly, we had to use the knowledge of  which is not available in general. Therefore, it is especially important to note that we were able to find the dead core solution without explicit knowledge of
which is not available in general. Therefore, it is especially important to note that we were able to find the dead core solution without explicit knowledge of  by treating the problem (3.10), formulated on the whole interval
by treating the problem (3.10), formulated on the whole interval  ,
,

instead of solving (3.16). In Figures 14 and 15, we report on the numerical test runs for  ,
,  , and two values of
, and two values of  ,
,  and
and  , respectively. In Figures 16 and 17, analogous results for
, respectively. In Figures 16 and 17, analogous results for  ,
,  , and
, and  ,
,  , respectively, can be found.
, respectively, can be found.
Table 2 contains the information on the exact global error of the numerical dead core solution. We report on its maximal value  for a wide range of parameters. Obviously, dead core solutions can be found without exact use of the known solution structure, but the initial profile must be chosen carefully to guarantee the Newton iteration to convergence.
for a wide range of parameters. Obviously, dead core solutions can be found without exact use of the known solution structure, but the initial profile must be chosen carefully to guarantee the Newton iteration to convergence.
3.4. Positive Solutions of Problem (1.5a)-(1.5b)
In this section, we deal with problem (1.5a)-(1.5b). Since this problem is very involved, we decided to simulate it numerically first in order to provide some preliminary information about its solution. The numerical treatment of (1.5a)-(1.5b) turned out to be not at all straightforward, but nevertheless, for a certain choice of parameters,  ,
,  ,
,  and
and  ,
,  , we were able to solve the problem and provide the error estimate and the residual for its approximative solution. We have applied the path following strategy implemented in bvpsuite to the boundary value problem
, we were able to solve the problem and provide the error estimate and the residual for its approximative solution. We have applied the path following strategy implemented in bvpsuite to the boundary value problem

In Figures 19 to 28, we present numerical results for problem (3.18). The values of  for which we were able to calculate the associated numerical solutions, are shown in Figure 18. According to Figure 18, we have found a turning point at
for which we were able to calculate the associated numerical solutions, are shown in Figure 18. According to Figure 18, we have found a turning point at  In a certain region below this value, there exist for any
In a certain region below this value, there exist for any  two different positive solutions.
two different positive solutions.
In order to start the path following procedure we set  and used
and used  as an initial profile. For each further step, we used the solution from the previous step as an initial profile. The solution corresponding to the values of
as an initial profile. For each further step, we used the solution from the previous step as an initial profile. The solution corresponding to the values of  shown in Figures 19 and 20 is unique. For
shown in Figures 19 and 20 is unique. For  we have found two different positive solutions, compare Figures 21 and 22. Also, for
we have found two different positive solutions, compare Figures 21 and 22. Also, for  , two different positive solutions exist; see Figures 23 and 24. Interestingly, solutions found in the vicinity of the turning point change rather fast, although the values of
, two different positive solutions exist; see Figures 23 and 24. Interestingly, solutions found in the vicinity of the turning point change rather fast, although the values of  do not; see Figures 25 to 26. Finally, in the last step of the procedure, we obtained a solution which nearly reaches a pseudo dead core solution with
do not; see Figures 25 to 26. Finally, in the last step of the procedure, we obtained a solution which nearly reaches a pseudo dead core solution with  .
.
References
Aris R: The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts. Clarendon Press, Oxford, UK; 1975.
Baxley JV, Gersdorff GS: Singular reaction-diffusion boundary value problems. Journal of Differential Equations 1995,115(2):441-457. 10.1006/jdeq.1995.1022
Agarwal RP, O'Regan D, Staněk S:Dead core problems for singular equations with
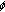 -Laplacian. Boundary Value Problems 2007, 2007:-16.
-Laplacian. Boundary Value Problems 2007, 2007:-16.Staněk S, Pulverer G, Weinmüller EB: Analysis and numerical simulation of positive and dead-core solutions of singular two-point boundary value problems. Computers & Mathematics with Applications 2008,56(7):1820-1837. 10.1016/j.camwa.2008.03.029
Agarwal RP, O'Regan D, Staněk S:Positive and dead core solutions of singular Dirichlet boundary value problems with
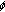 -Laplacian. Computers & Mathematics with Applications 2007,54(2):255-266. 10.1016/j.camwa.2006.12.026
-Laplacian. Computers & Mathematics with Applications 2007,54(2):255-266. 10.1016/j.camwa.2006.12.026Agarwal RP, O'Regan D, Staněk S:Dead cores of singular Dirichlet boundary value problems with
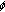 -Laplacian. Applications of Mathematics 2008,53(4):381-399. 10.1007/s10492-008-0031-z
-Laplacian. Applications of Mathematics 2008,53(4):381-399. 10.1007/s10492-008-0031-zBobisud LE: Asymptotic dead cores for reaction-diffusion equations. Journal of Mathematical Analysis and Applications 1990,147(1):249-262. 10.1016/0022-247X(90)90396-W
Bobisud LE: Behavior of solutions for a Robin problem. Journal of Differential Equations 1990,85(1):91-104. 10.1016/0022-0396(90)90090-C
Bobisud LE, O'Regan D, Royalty WD: Existence and nonexistence for a singular boundary value problem. Applicable Analysis 1988,28(4):245-256. 10.1080/00036818808839765
Auzinger W, Koch O, Weinmüller E: Efficient collocation schemes for singular boundary value problems. Numerical Algorithms 2002,31(1–4):5-25. 10.1023/A:1021151821275
Auzinger W, Kneisl G, Koch O, Weinmüller E: A collocation code for singular boundary value problems in ordinary differential equations. Numerical Algorithms 2003,33(1–4):27-39. 10.1023/A:1025531130904
Kitzhofer G: Numerical treatment of implicit singular BVPs, Ph.D. thesis. Institute for Analysis and Scientific Computing, Vienna University of Technology, Vienna, Austria;
Budd CJ, Koch O, Weinmüller E: Self-similar blow-up in nonlinear PDEs. Institute for Analysis and Scientific Computing, Vienna University of Technology, Vienna, Austria; 2004.
Budd CJ, Koch O, Weinmüller E: Computation of self-similar solution profiles for the nonlinear Schrödinger equation. Computing 2006,77(4):335-346. 10.1007/s00607-005-0157-8
Budd CJ, Koch O, Weinmüller E: Fron nonlinear PDEs to singular ODEs. Applied Numerical Mathematics 2006,56(3-4):413-422. 10.1016/j.apnum.2005.04.012
Kitzhofer G, Koch O, Lima P, Weinmüller E: Efficient numerical solution of the density profile equation in hydrodynamics. Journal of Scientific Computing 2007,32(3):411-424. 10.1007/s10915-007-9141-0
Rachůnková I, Koch O, Pulverer G, Weinmüller E: On a singular boundary value problem arising in the theory of shallow membrane caps. Journal of Mathematical Analysis and Applications 2007,332(1):523-541. 10.1016/j.jmaa.2006.10.006
Ascher UM, Mattheij RMM, Russell RD: Numerical Solution of Boundary Value Problems for Ordinary Differential Equations, Prentice Hall Series in Computational Mathematics. Prentice Hall, Englewood Cliffs, NJ, USA; 1988:xxiv+595.
Kitzhofer G, Koch O, Weinmüller EB: Pathfollowing for essentially singular boundary value problems with application to the complex Ginzburg-Landau equation. BIT. Numerical Mathematics 2009,49(1):141-160. 10.1007/s10543-008-0208-6
Acknowledgments
This work was supported by the Austrian Science Fund Project P17253 and supported by Grant no. A100190703 of the Grant Agency of the Academy of Science of the Czech Republic and by the Council of Czech Government MSM 6198959214.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pulverer, G., Staněk, S. & Weinmüller, E.B. Analysis and Numerical Solutions of Positive and Dead Core Solutions of Singular Sturm-Liouville Problems. Adv Differ Equ 2010, 969536 (2010). https://doi.org/10.1155/2010/969536
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/969536
 and the number and types of solutions to problem (1.6a)-(1.6b), provided that
and the number and types of solutions to problem (1.6a)-(1.6b), provided that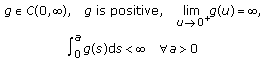
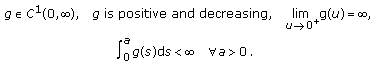
 to the singular boundary value problem
to the singular boundary value problem 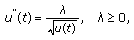

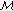 . In addition, for each
. In addition, for each  , problem (1.6a)-(1.6b) with
, problem (1.6a)-(1.6b) with 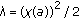 has a unique positive solution such that
has a unique positive solution such that  ,
,  .
.
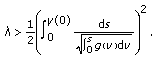
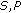 on
on 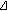 by
by 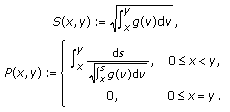
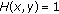 , that is,
, that is, 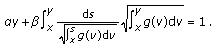

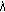
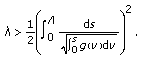
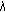 satisfying (2.58), problem (1.6a)-(1.6b) has a unique dead core solution.
satisfying (2.58), problem (1.6a)-(1.6b) has a unique dead core solution. is the dead core of a dead core solution
is the dead core of a dead core solution  of problem (1.6a)-(1.6b), then
of problem (1.6a)-(1.6b), then 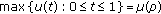 and
and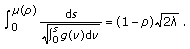
 be a dead core solution of problem (1.6a)-(1.6b) for some
be a dead core solution of problem (1.6a)-(1.6b) for some 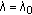 and let
and let  . Then there exists a point
. Then there exists a point 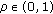 such that
such that 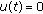 for
for  , and equalities (2.39), (2.40), and (2.41) are satisfied by Lemma 2.9. We deduce from (2.41) and from Lemma 2.4 that
, and equalities (2.39), (2.40), and (2.41) are satisfied by Lemma 2.9. We deduce from (2.41) and from Lemma 2.4 that 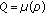 . Therefore, compare (2.40),
. Therefore, compare (2.40), 
 satisfying (2.58). By (i), problem (1.6a)-(1.6b) has a dead core solution which is unique by Lemma 2.9.
satisfying (2.58). By (i), problem (1.6a)-(1.6b) has a dead core solution which is unique by Lemma 2.9. be the dead core of a dead core solution
be the dead core of a dead core solution  of problem (1.6a)-(1.6b). Then, by Lemma 2.9, equalities (2.40) and (2.41) hold with
of problem (1.6a)-(1.6b). Then, by Lemma 2.9, equalities (2.40) and (2.41) hold with  replaced by
replaced by 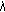 and
and  . Since
. Since  by the definition of the function
by the definition of the function  , we have
, we have 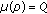 . Equality (2.59) now follows from (2.40) with
. Equality (2.59) now follows from (2.40) with 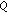 and
and  replaced by
replaced by 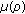 and
and 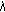 , respectively.
, respectively.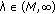 , there exists only a unique dead core solution of problem (1.9a)-(1.9b).
, there exists only a unique dead core solution of problem (1.9a)-(1.9b). , there exist a unique dead core solution and a unique positive solution of problem (1.9a)-(1.9b).
, there exist a unique dead core solution and a unique positive solution of problem (1.9a)-(1.9b).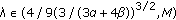 , there exist a unique dead core solution and exactly two positive solutions of problem (1.9a)-(1.9b).
, there exist a unique dead core solution and exactly two positive solutions of problem (1.9a)-(1.9b). , there exist the unique pseudo dead core solution
, there exist the unique pseudo dead core solution  and a unique positive solution of problem (1.9a)-(1.9b).
and a unique positive solution of problem (1.9a)-(1.9b).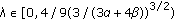 , there exist only a unique positive solution of problem (1.9a)-(1.9b).
, there exist only a unique positive solution of problem (1.9a)-(1.9b). is the (unique) positive solution of problem (1.9a)-(1.9b) with
is the (unique) positive solution of problem (1.9a)-(1.9b) with  , then
, then  , where
, where 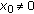 is the root of the equation
is the root of the equation 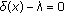 .
. are the (unique) positive solutions of problem (1.9a)-(1.9b) with
are the (unique) positive solutions of problem (1.9a)-(1.9b) with  , then
, then 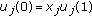 ,
, 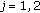 , where
, where 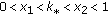 , are the roots of the equation
, are the roots of the equation 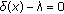 .
.
 for
for  (a) and for
(a) and for  ,
,  (b).
(b).
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  . The associated root is
. The associated root is  .
.
 ,
,  and
and  . The associated root is
. The associated root is  .
.
 ,
,  and
and  . The associated root is
. The associated root is  .
.
 ,
,  and
and  . The associated root is
. The associated root is  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 ,
,  and
and  .
.
 path obtained in 76 steps of the path following procedure, where
path obtained in 76 steps of the path following procedure, where  . The turning point has been found at
. The turning point has been found at  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
. -Laplacian. Boundary Value Problems 2007, 2007:-16.
-Laplacian. Boundary Value Problems 2007, 2007:-16. -Laplacian. Computers & Mathematics with Applications 2007,54(2):255-266. 10.1016/j.camwa.2006.12.026
-Laplacian. Computers & Mathematics with Applications 2007,54(2):255-266. 10.1016/j.camwa.2006.12.026 -Laplacian. Applications of Mathematics 2008,53(4):381-399. 10.1007/s10492-008-0031-z
-Laplacian. Applications of Mathematics 2008,53(4):381-399. 10.1007/s10492-008-0031-z