- Research Article
- Open access
- Published:
From Newton's Equation to Fractional Diffusion and Wave Equations
Advances in Difference Equations volume 2011, Article number: 169421 (2011)
Abstract
Fractional calculus represents a natural instrument to model nonlocal (or long-range dependence) phenomena either in space or time. The processes that involve different space and time scales appear in a wide range of contexts, from physics and chemistry to biology and engineering. In many of these problems, the dynamics of the system can be formulated in terms of fractional differential equations which include the nonlocal effects either in space or time. We give a brief, nonexhaustive, panoramic view of the mathematical tools associated with fractional calculus as well as a description of some fields where either it is applied or could be potentially applied.
1. Introduction
Fractional calculus (see [1]) offers a very suggestive and stimulating scenario where we have the convergence of deep and fundamental mathematical questions, development of appropriate numerical algorithms, as well as the applications to modelizations in different frameworks. An illustration of the physical applications of fractional calculus is the recent following books and special issues on applications on nanotechnology and other important topics [2–6], among many others.
From a mathematical point of view, the modelization of the long-range dependence is associated with integrodifferential equations in a broad sense. On the other hand, in many cases such integrodifferential equations can be understood as fractional differential equations, and they can be studied in the fractional calculus framework.
Up to 1994, a very extensive review about the nonlinear nonlocal wave equations with applications in hydrodynamics, magnetohydrodynamics, and plasma can be found in the book of Naumkin and Shishmarëv [7]. The nonlocality in space is associated with the long-range interactions (many space scales) while the nonlocality in time is related to the effects with memory/delay (many time scales). The corresponding nonlocal systems are described by general integral equations. We have a large spectrum of scenarios where the integral equations occur [8–15]: potential theory, signal processing, problems in geophysics, problems in electricity and magnetism, hereditary phenomena in physics and biology, problems in population growth and industrial replacement, radiation problems, optimization, and automatic control systems, communication theory, stochastic problems, and mathematical economics and financial phenomena.
Professor Magin in his recent book, Fractional Calculus in Bioengineering [16] established clearly the underlying mathematical context of fractional calculus.
The purpose of this book is to explore the behavior of biological systems from the perspective of fractional calculus. Fractional calculus, integration and differentiation of an arbitrary or fractional order, provides new tools that expand the descriptive power of calculus beyond the familiar integer-order concepts of rates of change and area under a curve… Fractional calculus adds new functional relationships and new functions to the familiar family of exponentials and sinusoids that arise in the realm of ordinary linear differential equations. Among such functions that play an important role, we have the Euler Gamma function, the Euler Beta function, the Mittag-Leffler functions, the Wright and Fox functions, and so forth.
From a historical point of view, the origin of fractional calculus coincides with that of differential calculus. In a letter [17] dated September 9, 1695, and addressed to G. Leibniz, M. de L'Hopital raises the question of the possible meaning of  if
if  . The answer of Leibniz was: "
. The answer of Leibniz was: " will be equal to
will be equal to
 . This is an apparent paradox from which, one day, useful consequences will be drawn". Fractional calculus arises to give a meaning to the noninteger derivatives. This concept was also analyzed by E. Euler, J. Liouville, P. S. Laplace, or Fourier. The generalization of this framework indicates that it is more appropriate to talk of integration and differentiation of arbitrary order. The book by Samko et al. [1] reflects the situation of fractional calculus up to 1990 with a wide bibliography and many applications. Therefore we can think in the field of Fractional Calculus as an old topic, but, from 20 years ago, the real applications of the so-called fractional models in so many branches of applied sciences and engineering have increased in a dramatic way, so we can consider the topic of fractional differential equations and their applications as a emergent field.
. This is an apparent paradox from which, one day, useful consequences will be drawn". Fractional calculus arises to give a meaning to the noninteger derivatives. This concept was also analyzed by E. Euler, J. Liouville, P. S. Laplace, or Fourier. The generalization of this framework indicates that it is more appropriate to talk of integration and differentiation of arbitrary order. The book by Samko et al. [1] reflects the situation of fractional calculus up to 1990 with a wide bibliography and many applications. Therefore we can think in the field of Fractional Calculus as an old topic, but, from 20 years ago, the real applications of the so-called fractional models in so many branches of applied sciences and engineering have increased in a dramatic way, so we can consider the topic of fractional differential equations and their applications as a emergent field.
A nonexhaustive list of works that support the mentioned modern development of fractional calculus and its applications are in [18–25]. From our point of view, the monographic work by Metzler and Klafter in 2000 [26] could be considered as the last breakpoint in developing the field of the study of fractional differential equations and their applications. Some of the more important publications on the mentioned topic during last five years, among so many references, could be the following books in [27–34].
There are different definitions of fractional derivatives and, as a consequence, of fractional integrals, since the fractional derivation is the inverse operation of the fractional integration. This a generalization of what happens in ordinary calculus with the standard integer derivatives and integrals according to the fundamental theorem of calculus. The different fractional derivatives coincide in the integer case, up to a constant in some cases. We have the fractional derivatives and integrals of Riemann-Liouville, Liouville, Caputo, and so forth, and their general feature is the nonlocal character since they depend on the values of the function in an interval. As an illustration, we have a derivative of order  of the function
of the function  :
:

where  and
and  . This definition requires the absolute integrability of the derivative of order
. This definition requires the absolute integrability of the derivative of order  .
.
The nonlocal character makes the fractional derivatives suitable for the modellization of systems with long-range interactions. On the other hand, the freedom in the definition of fractional derivatives allows us to incorporate different types of information. At the same time, the fractional derivatives with noninteger exponents stress which algebraic scale properties are relevant to the data analysis.
In this contribution, we present a standard approach to construct fractional differential equations from the basic equations of classical and quantum mechanics (Section 2). In Section 3, we analyze the possible bridges between fractional calculus and fractals while in Section 4, we consider the relation of fractional calculus with the modellization of relaxation processes.
2. Fractional Differential Equations
Following the models of classical mechanics ([35]) and quantum mechanics ([36]), let us consider a possible standard path among the basic equations of physics that would allow us to interpret, in a more wide context, the level offractionalization of the basic differential equations by analyzing the associated dynamics and solutions in the framework of the corresponding modellization [26, 27, 37–39].
For the sake of simplicity, let us consider systems in one space dimension. Newton's equation for a particle of mass  moving in a one-dimensional force field
moving in a one-dimensional force field  ,
,  being the displacement, is
being the displacement, is

Let us consider now a discrete system, formed by infinite point-like masses,  , spaced a distance
, spaced a distance  , and connected by strings of the same constant
, and connected by strings of the same constant  . If we name
. If we name  the displacement of the particle
the displacement of the particle  from the equilibrium, the equation of motion is given by
from the equilibrium, the equation of motion is given by

This equation is written in such a way as to interpret appropriately the continuous limit of the system when  :
:

Thus, we have the equation

where  . With this mechanical approach, we get the wave equation which appears in many contexts according to the different meanings of
. With this mechanical approach, we get the wave equation which appears in many contexts according to the different meanings of  and
and  . If we assume a damping mechanism either in the discrete system or in the continuous limit, we have the equation
. If we assume a damping mechanism either in the discrete system or in the continuous limit, we have the equation

When the damping term,  , dominates over the inertial one,
, dominates over the inertial one,  , we have the standard diffusion equation
, we have the standard diffusion equation

Other basic equations are obtained by considering extra linear terms. This is the case of the Klein-Gordon equation:

and the Telegraph equation:

All this can be summarized in the following equation, where we also include Dirac's equation to be discussed in the following paragraphs.

According to the previous statements, we have a set of very important features.
-
(i)
Fractional calculus provides a natural interpolation between different equations. For instance, we have the fractional interpolation between the wave equation (hyperbolic) and the diffusion equation (parabolic). Thus, we have the family of fractional equations
 (2.10)
(2.10)When
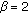 we have the wave equation, while we have the diffusion equation for
we have the wave equation, while we have the diffusion equation for  . The study of such possible interpolations has not been fully exploited yet.
. The study of such possible interpolations has not been fully exploited yet. -
(ii)
The different equations above can be fractionalized by replacing the integer derivatives either in space or time by fractional derivatives. The range of fractional equations is very wide at the same time that the exploration of the associated dynamics and solutions is a task to be fulfilled. On the other hand, it is an open issue to analyze the relation of the different fractionalizations at the discrete and the continuous levels.
-
(iii)
The standard diffusion equation. The diffusion equation (2.6) appears in very different physical contexts which leads to a better understanding and interpretation of the generalized diffusion equations. Such different applications allow a richer phenomenology to understand the possible meaning of the different possible fractionalizations. As an example, the equation is obtained by combining the following laws with the associated continuity equation.
-
(iv)
Darcy's law
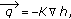 (2.11)
(2.11)where
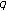 is the flux of groundwater,
is the flux of groundwater, 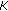 is the medium property: hydraulic conductivity, and
is the medium property: hydraulic conductivity, and  is the potential related to the head.
is the potential related to the head. -
(v)
Fourier's law
 (2.12)
(2.12)where
 is the flux of heat,
is the flux of heat,  is the medium property: thermal conductivity and
is the medium property: thermal conductivity and 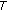 is the potential related to the temperature.
is the potential related to the temperature. -
(vi)
Fick's law
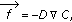 (2.13)
(2.13)where
 is the flux of solute,
is the flux of solute,  is the medium property: diffusion coefficient and
is the medium property: diffusion coefficient and 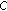 is the potential related to the concentration.
is the potential related to the concentration. -
(vii)
Ohm's law
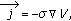 (2.14)
(2.14)where
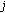 is the flux of charge (electrical current),
is the flux of charge (electrical current),  is the medium property: electrical conductivity, and
is the medium property: electrical conductivity, and 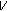 is the potential related to the voltage.
is the potential related to the voltage. -
(viii)
The fractional Dirac equation (see [11, 40–43]). The free Dirac equation ([36]) can be considered as the square root of the Klein-Gordon equation. This is also true for the case of
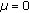 in (2.7) which corresponds to the wave equation. More precisely in this last case, we have Figure 1: where
in (2.7) which corresponds to the wave equation. More precisely in this last case, we have Figure 1: where 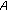 and
and 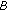 are matrices satisfying the indicated algebra. The function
are matrices satisfying the indicated algebra. The function 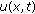 is scalar while
is scalar while  is a multicomponent function with, at least, two scalar space-time components.
is a multicomponent function with, at least, two scalar space-time components.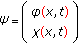 (2.15)
(2.15)
In the context of Figure 1, we can understand the following equation:

as the square root of the standard diffusion equation (2.6). It is another way to view the possible interpolations between the hyperbolic operator of the wave equation and the parabolic one of the classical diffusion equation. Every scalar component of  also satisfies the diffusion equation above. Such solutions can be interpreted as probability distributions with internal structure associated to internal degrees of freedom of the system. We could name them diffunors in analogy with the spinors of quantum mechanics.
also satisfies the diffusion equation above. Such solutions can be interpreted as probability distributions with internal structure associated to internal degrees of freedom of the system. We could name them diffunors in analogy with the spinors of quantum mechanics.
According to the possible representations of the Pauli algebra for  and
and  , we have either an uncoupled system or a coupled system of equations. An example of the first case is the representation
, we have either an uncoupled system or a coupled system of equations. An example of the first case is the representation

The transition between the two limit behaviours indicated in the diagram is not well understood and it deserves a deep analysis. As an illustration of the possible rich phenomenology associated to the interpolating fractional wave and Dirac equations is their behaviour with respect the discrete symmetries: time  and space inversion
and space inversion  (see [43]).
(see [43]).
This analysis of the fractional wave, diffusion, and Dirac equations, fits in the general context of establish bridges between fractional calculus and the classical and quantum mechanics [44, 45]. This is also the approach of the works of Rabei and coworkers (see [46]).
3. Fractional Calculus and Fractals
Fractals and fractional calculus generate parameters of intermediate order: arbitrary dimensions as well as arbitrary order of integration and differentiation [47, 48]. Let us consider the basic aspects associated with both conceptual blocks, and we will remark on possible bridges between them to be explored.
-
(1)
Fractals show self-similar structures, being the same structure at all scale levels. Such structures are introduced by using the concept of a reference structure and repeating itself over many scales, telescoping both downward and upward in scale. In general, the fractals structures are defined by an iterative process instead of an explicit mathematical formula. A simple case is the Cantor set which is a limiting set of points which results from discarding the middle third of each line segment in going from generation to generation, and starting from a line segment of unit length. The fractal dimension D is a measure of the irregularity of the fractal structure, and, in the case of the Cantor set, the fractal dimension is
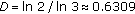 .
.The fractal property can be either in space or in time. In the first case we have the fractal geometric structures as the Cantor set while in the temporal context we have the structures of sequence of data generated for a system over an interval of time. A special case is the Weierstrass function which is an example of a function continuous everywhere but differentiable nowhere:
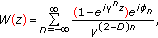 (3.1)
(3.1)where
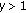 ,
,  is an arbitrary phase and
is an arbitrary phase and 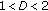 ,
, 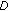 being the fractal dimension of the self-similar structure defined by
being the fractal dimension of the self-similar structure defined by 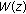 . The function can be interpreted as a superposition of harmonic terms: the first one with unit amplitude and unit frequency and the
. The function can be interpreted as a superposition of harmonic terms: the first one with unit amplitude and unit frequency and the  -order term with amplitude
-order term with amplitude 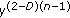 and frequency
and frequency  . The lack of differentiability of
. The lack of differentiability of 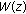 is related to the integer derivatives. On the other hand, it has been established that the fractional derivative (fractional integral) of the Weierstrass function is another fractal function with a greater (lesser) fractal dimension [49]. At the same time, it has been proved that the Weierstrass function is a solution of a fractional differential stochastic equation of motion. In particular, we have the following relations for the Weierstrass function.
is related to the integer derivatives. On the other hand, it has been established that the fractional derivative (fractional integral) of the Weierstrass function is another fractal function with a greater (lesser) fractal dimension [49]. At the same time, it has been proved that the Weierstrass function is a solution of a fractional differential stochastic equation of motion. In particular, we have the following relations for the Weierstrass function.-
(i)
The fractional Riemann-Liouville integral of order
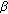 , with
, with  :
: (3.2)
(3.2) -
(ii)
The fractional Riemann-Liouville derivative of order
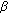 , with
, with 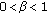 :
: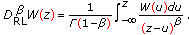 (3.3)
(3.3) -
(iii)
The relation between the fractal dimensions of the fractional derivative and integral of the Weierstrass function
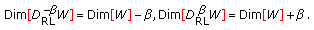 (3.4)
(3.4)
-
(i)
-
(2)
One of the possible experimental contexts to apply together with the concepts of fractals and fractional calculus is related to the propagation of waves [50–52]. In the 19th Century, James Clerk Maxwell and Lord Rayleigh studied the interaction of electromagnetic waves with Euclidean regular structures (cylinders, spheres). On the other hand, there are either nonregular artificial structures or from nature that show many length scales and they are not suitable to be studied in the Euclidean context. This is the case of nonregular surfaces, disordered media, structures with specific properties of scattering, and so forth. In this context, the fundamental issue of special technological impact is the relation between the geometrical parameters (structure descriptors) and the physical quantities that characterize electromagnetically the system. For instance, a relevant information is the relation between the fractal dimension of the scattering surface and the scattered wave. Related to that, we have that a recent field of research has been to explore the possible links between the fractional calculus and the electromagnetic theory ([53]). The fractionalization of certain linear operators in electromagnetic theory has led to relevant solutions in radiation and scattering problems.
As a simple illustration, let us consider the propagation of a wave in fractal media. The geometrical optics cannot be applied and the eikonal equation is no longer valid since it applies for wave lengths  dimension of any change in the media. This condition cannot be satisfied for fractal media because, in this case, there is no characteristic length of the system. We can consider the associated stationary eigenvalue problem that appears in two contexts: the wave equation in a fractal potential and the wave equation with fractal boundary conditions. In the last case, we have the general equation
dimension of any change in the media. This condition cannot be satisfied for fractal media because, in this case, there is no characteristic length of the system. We can consider the associated stationary eigenvalue problem that appears in two contexts: the wave equation in a fractal potential and the wave equation with fractal boundary conditions. In the last case, we have the general equation

where  is a linear differential operator on
is a linear differential operator on  with boundary conditions
with boundary conditions  on a nondifferentiable surface but which admits the fractional derivative
on a nondifferentiable surface but which admits the fractional derivative  with
with  . If we define
. If we define  , we have the problem
, we have the problem  with the boundary condition
with the boundary condition  ,
,  being differentiable. Thus, with the help of the fractional derivative, we transformed the original boundary problem into another one more suitable to be studied.
being differentiable. Thus, with the help of the fractional derivative, we transformed the original boundary problem into another one more suitable to be studied.
4. Fractional Calculus and Relaxation Processes
In the study of the behavior of the materials under applied forces, we have two ideal relations between such forces and the resultant displacements in the material which are represented by linear differential equations.
-
(i)
Linear elastic behavior which is described by the Hooke's law (ideal solid):
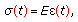 (4.1)
(4.1)where
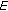 is Young's modulus,
is Young's modulus, 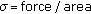 is the stress and
is the stress and 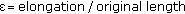 is the strain of the corresponding mechanical model, that, in this case, is represented by a spring characterized by the constant
is the strain of the corresponding mechanical model, that, in this case, is represented by a spring characterized by the constant 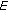 .
. -
(ii)
Ideal viscous fluid behavior which is described by Newton's fluid law (ideal fluid):
 (4.2)
(4.2)where
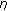 is the viscosity coefficient, and, in this case, the phenomenological model is represented by a dashpot.
is the viscosity coefficient, and, in this case, the phenomenological model is represented by a dashpot.
In general, the real materials exhibit characteristics which combine the behaviors of the ideal solids and liquids and are named viscoelastic materials. The basic models of such materials are based on combinations of springs and dashpots [2, 16, 54]. As an illustration, let us consider the combination of a spring and a dashpot in series. In this case, the stresses are equal for both structural parts while the strains add. This leads to the classical Maxwell model which is described by the following linear differential equation obtained from the above two equations:

where  . If we consider the Laplace transform of the above equation, we obtain the relaxation modulus
. If we consider the Laplace transform of the above equation, we obtain the relaxation modulus
 . Finally, the stress relaxation modulus for the Maxwell model is
. Finally, the stress relaxation modulus for the Maxwell model is

which indicates that the Maxwell model shows an exponential stress decay, while different behaviors are observed in real materials. Fractional calculus allow us to introduce generalizations of the Maxwell model and the basic constitutive equation that leads to more general behaviors of the stress relaxation modulus.
-
(i)
The fractional constitutive equation
 (4.5)
(4.5)which is an interpolation between Hooke's law
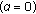 and Newton's law
and Newton's law  . This fractional relation can be realized physically through hierarchical arrangements and in the limit of an infinite number of springs and dashpots [2].
. This fractional relation can be realized physically through hierarchical arrangements and in the limit of an infinite number of springs and dashpots [2]. -
(ii)
The general fractional Maxwell equation offers a wide range of possible behaviors
 (4.6)
(4.6)the solutions are well analyzed in [2, 16] as well as in the references therein.
-
(iii)
In order to consider other generalizations and approaches for possible different applications, we can interpret the relaxation process either as an initial value problem or a memory problem.
-
(a)
Initial Value Problem. The relaxation (4.4) can be interpreted as the solution of the initial value problem
 (4.7)
(4.7)with solution
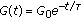 . From (4.7), we can write as starting point for the fractional generalization:
. From (4.7), we can write as starting point for the fractional generalization: (4.8)
(4.8)from which, we formally get the fractional generalization
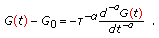 (4.9)
(4.9) -
(b)
Memory Problem. Another natural generalization of (4.7) is
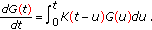 (4.10)
(4.10)
-
(a)
If  , we recover the exponential behavior of the Maxwell model (4.4). If we have constant memory,
, we recover the exponential behavior of the Maxwell model (4.4). If we have constant memory,  , we have the periodic behavior:
, we have the periodic behavior:  . Finally, if
. Finally, if  with
with  , the equation (4.10) can be written as a fractional derivative and the solution can be expressed in terms of the Fox functions.
, the equation (4.10) can be written as a fractional derivative and the solution can be expressed in terms of the Fox functions.
One possible application field for fractional calculus would be the modellization of the shape memory alloys (SMA). These are basically materials that change shape when energy is applied or extracted from them. They exhibit hardness and elasticity properties that change radically at distinct temperatures [55]. There is a high complexity in the relation between the microscopic and macroscopic behaviors. There are no reliable constitutive models, although some have been studied by Tanaka [56], Liang and Rogers [57], and Brinson [58]. The key feature of these materials, as the name indicates, is that their dynamics is memory dependent. Thus, the possible realistic models should include the nonlocal effects in time through integrodifferential equations and, possibly, fractional differential equations.
References
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science, Yverdon, Switzerland; 1993:xxxvi+976.
Hilfer R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Hilfer R, Metzler R, Blumen A, Klafter J (Eds): Strange kinetics In Chemical Physics 2002,284(1):1-541. 10.1016/S0301-0104(02)00801-7
Baleanu D, Güvenç ZB, Tenreiro Machad JA: New Trends in Nanotechnology and Fractional Calculus Applications. Springer, New York, NY, USA; 2010:xii+531.
Ortigueira M, Tenreiro-Machado JA, Trujillo JJ, Vinagre B (Eds): Advances in fractional signals and systems In Journal of Signal Processing 2011,91(3):349-606. 10.1016/j.sigpro.2010.08.002
Tenreiro-Machado JA, Luo A (Eds): Discontinuous and fractional dynamical systems In Journal of Computational and Nonlinear Dynamics 2008,3(2):1-125.
Naumkin PI, Shishmarëv IA: Nonlinear Nonlocal Equations in the Theory of Waves, Translations of Mathematical Monographs. Volume 133. American Mathematical Society, Providence, RI, USA; 1994:x+289.
Lonseth AT: Sources and applications of integral equations. SIAM Review 1977,19(2):241-278. 10.1137/1019039
Cheney M, Borden B: Fundamentals of Radar Imaging, CBMS-NSF Regional Conference Series in Applied Mathematics. Volume 79. SIAM, Philadelphia, Pa, USA; 2009:xxiv+140.
Baillie RT, King ML (Eds): Fractional differencing and long memory processes In Journal of Econometrics 1996,73(1):1-324. 10.1016/0304-4076(95)01731-3
Vázquez L: A fruitful interplay: from nonlocality to fractional calculus. In Nonlinear Waves: Classical and Quantum Aspects. Edited by: Abdullaev FKh, Konotop VV. Kluwer Academic Publishers, New York, NY, USA; 2004:129-133.
Vázquez L, Usero D: Nonlocal equations and fractional models. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales (España) 2005,99(2):203-223.
Vázquez L, Evans WAB, Rickayzen G: Numerical investigation of a non-local sine-Gordon model. Physics Letters A 1994,189(6):454-459. 10.1016/0375-9601(94)91209-2
Alfimov GL, Usero D, Vázquez L:On complex singularities of solutions of the equation
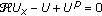 . Journal of Physics A 2000,33(38):6707-6720. 10.1088/0305-4470/33/38/305
. Journal of Physics A 2000,33(38):6707-6720. 10.1088/0305-4470/33/38/305Pipiras V, Taqqu MS: Fractional calculus and its connections to fractional Brownian motion. In Theory and Applications of Long-Range Dependence. Edited by: Doukhan P, Oppenheim G, Taqqu MS. Birkhäuser, Boston, Mass, USA; 2003:165-201.
Magin RL: Fractional Calculus and Bioengineering. Begell House, New York, NY, USA; 2006.
Leibniz GW: Oeuvres Mathematiques de Leibniz. Correpondence de leibniz avec Huygens, van Zulichem et le Marquis de L'Hospital Part 1. Volume 2. Libr. de A. Franck, Paris, France; 1853.
Oldham KB, Spanier J: The Fractional Calculus, Mathematics in Science and Engineering. Volume 11. Academic Press, New York, NY, USA; 1974:xiii+234.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Oustaloup A: La Drivation Non Entiere. Theorie, Synthese et Applications. Hermes Science, Stanmore, UK; 1995.
Kiryakova V: Generalized Fractional Calculus and Applications, Pitman Research Notes in Mathematics Series. Volume 301. Longman Scientific & Technical, Harlow, UK; 1994:x+388.
Podlubny I: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Rubin B: Fractional Integrals and Potentials, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 82. Longman, Harlow, UK; 1996:xiv+409.
Bonilla B, Kilbas AA, Trujillo JJ: Cálculo Fraccionario y Ecuaciones Diferenciales Fraccionarias. Serv. de Publicaciones de la UNED, Madrid, Spain; 2003.
Zaslavsky GM: Chaos, fractional kinetics, and anomalous transport. Physics Reports 2002,371(6):461-580. 10.1016/S0370-1573(02)00331-9
Metzler R, Klafter J: The random walk's guide to anomalous diffusion: a fractional dynamics approach. Physics Reports 2000,339(1):77.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Zaslavsky GM: Hamiltonian Chaos and Fractional Dynamics. Oxford University Press, Oxford, UK; 2008:xiv+421.
Uchaikin VV: Method of Fractional Derivatives. Artishok-Press, Ulyanovsk, Russia; 2008.
Lakshmikantham V, Leela S, Vasundhara-Devi J: Theory of Fractional Dynamic Systems. Cambridge Scientific Publishers, Cambridge, UK; 2009.
Mainardi F: Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Imperial College Press, London, UK; 2010:xx+347.
Caponetto R, Dongola G, Fortuna L, Petras I: Fractional Order Systems: Modeling and Control Applications. World Scientific, Singapure; 2010.
Tarasov VE: Fractional Dynamics in Physics. Higher Education Press and Springer, Berlin, Geramny; 2011.
Klafter J, Lim SC, Metzler R (Eds): Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. World Scientific, Singapore; 2011.
Goldstein H: Classical Mechanics. Addison-Wesley Press, Cambridge, Mass, USA; 1951:xii+399.
Dirac PAM: The Principles of Quantum Mechanics. Oxford University Press, Oxford, UK; 1958.
Sokolov IM, Klafter J, Blumen A: Fractional kinetics. Physics Today 2002,55(11):48-54. 10.1063/1.1535007
Jiménez S, Pascual P, Aguierre C, Vázquez L: A panoramic view of some perturbed nonlinear wave equations. International Journal of Bifurcation and Chaos 2004,14(1):1-40. 10.1142/S0218127404009211
Mendes RV, Vázquez L: The dynamical nature of a backlash system with and without fluid friction. Nonlinear Dynamics 2007,47(4):363-366. 10.1007/s11071-006-9035-y
Vázquez L: Fractional diffusion equations with internal degrees of freedom. Journal of Computational Mathematics 2003,21(4):491-494.
Vázquez L, Vilela Mendes R: Fractionally coupled solutions of the diffusion equation. Applied Mathematics and Computation 2003,141(1):125-130. 10.1016/S0096-3003(02)00326-0
Kilbas AA, Pierantozzi T, Trujillo JJ, Vázquez L: On the solution of fractional evolution equations. Journal of Physics A 2004,37(9):3271-3283. 10.1088/0305-4470/37/9/015
Pierantozzi T, Vázquez L: An interpolation between the wave and diffusion equations through the fractional evolution equations Dirac like. Journal of Mathematical Physics 2005,46(11):113512, 12.
Vázquez L: Una panorámica del Cálculo Fraccionario y sus aplicaciones. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales 2004,98(1):17-26.
Turchetti G, Usero D, Vázquez L: Hamiltonian systems with fractional time derivative. Tamsui Oxford Journal of Mathematical Sciences 2002,18(1):31-44.
Rabei EM, Nawafleh KI, Hijjawi RS, Muslih SI, Baleanu D: The Hamilton formalism with fractional derivatives. Journal of Mathematical Analysis and Applications 2007,327(2):891-897. 10.1016/j.jmaa.2006.04.076
West BJ, Bologna M, Grigolini P: Physics of Fractal Operators. Springer, New York, NY, USA; 2003:x+354.
Mandelbrot BB: The Fractal Geometry of Nature. W. H. Freeman, San Francisco, Calif, USA; 1982:v+460.
Rocco A, West BJ: Fractional calculus and the evolution of fractal phenomena. Physica A 1999,265(3):535-546. 10.1016/S0378-4371(98)00550-0
Berry MV: Difractals. Journal of Physics A 1979, 12: 781-797. 10.1088/0305-4470/12/6/008
Jaggard DL: On fractal electrodymanics. In Recent Advances in Electromagnetic Theory. Edited by: Kritikos HN, Jaggard DL. Springer, Berlin, Germany; 1990:183-224.
Konotop VV, Fei Z, Vázquez L: Wave interaction with a fractal layer. Physical Review E 1993,48(5):4044-4048. 10.1103/PhysRevE.48.4044
Engheta N: Fractional paradigm in electromagnetic theory. In Frontiers in Electromagnetism. Edited by: Werner DH, Mittra R. IEEE Press, New York, NY, USA; 2000:523-552.
Vázquez L, Velasco Cebrián MP: Aplicación del Cálculo Fraccionario a los procesos de relajación. Memorias de la Real Academia de Ciencias Exactas, Físicas y Naturales 2009, 23: 105-115.
Sun QP, Hwang KC: Micromechanics modelling for the constitutive behavior of polycrystalline shape memory alloys-II. Study of the individual phenomena. Journal of the Mechanics and Physics of Solids 1993,41(1):19-33. 10.1016/0022-5096(93)90061-J
Tanaka K: A thermo-mechanical sketch of shape memory effect: one-dimensional tensile behavior. Res Mechanica 1986,18(3):251-263.
Liang C, Rogers CA: One-dimensional thermo-mechanical constitutive relations for shape memory materials. Journal of Intelligent Material Systems and Structures 1990,1(2):207-218. 10.1177/1045389X9000100205
Brinson LC: One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable. Journal of Intelligent Material Systems and Structures 1993,4(2):229-242. 10.1177/1045389X9300400213
Acknowledgments
This paper has been partially supported by the Ministerio de Ciencia e Innovación of Spain under Grant AYA2009-14212-C05-05 and by FCT and POCI 2010 (Project MAT/58321/2004) with participation of FEDER.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vázquez, L. From Newton's Equation to Fractional Diffusion and Wave Equations. Adv Differ Equ 2011, 169421 (2011). https://doi.org/10.1155/2011/169421
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/169421

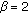 we have the wave equation, while we have the diffusion equation for
we have the wave equation, while we have the diffusion equation for  . The study of such possible interpolations has not been fully exploited yet.
. The study of such possible interpolations has not been fully exploited yet.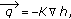
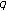 is the flux of groundwater,
is the flux of groundwater, 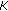 is the medium property: hydraulic conductivity, and
is the medium property: hydraulic conductivity, and  is the potential related to the head.
is the potential related to the head.
 is the flux of heat,
is the flux of heat,  is the medium property: thermal conductivity and
is the medium property: thermal conductivity and 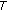 is the potential related to the temperature.
is the potential related to the temperature.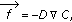
 is the flux of solute,
is the flux of solute,  is the medium property: diffusion coefficient and
is the medium property: diffusion coefficient and 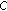 is the potential related to the concentration.
is the potential related to the concentration.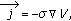
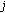 is the flux of charge (electrical current),
is the flux of charge (electrical current),  is the medium property: electrical conductivity, and
is the medium property: electrical conductivity, and 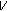 is the potential related to the voltage.
is the potential related to the voltage.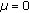 in (2.7) which corresponds to the wave equation. More precisely in this last case, we have Figure
in (2.7) which corresponds to the wave equation. More precisely in this last case, we have Figure 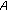 and
and 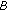 are matrices satisfying the indicated algebra. The function
are matrices satisfying the indicated algebra. The function 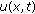 is scalar while
is scalar while  is a multicomponent function with, at least, two scalar space-time components.
is a multicomponent function with, at least, two scalar space-time components.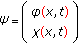

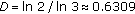 .
.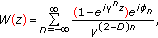
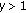 ,
,  is an arbitrary phase and
is an arbitrary phase and 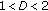 ,
, 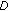 being the fractal dimension of the self-similar structure defined by
being the fractal dimension of the self-similar structure defined by 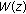 . The function can be interpreted as a superposition of harmonic terms: the first one with unit amplitude and unit frequency and the
. The function can be interpreted as a superposition of harmonic terms: the first one with unit amplitude and unit frequency and the  -order term with amplitude
-order term with amplitude 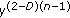 and frequency
and frequency  . The lack of differentiability of
. The lack of differentiability of 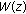 is related to the integer derivatives. On the other hand, it has been established that the fractional derivative (fractional integral) of the Weierstrass function is another fractal function with a greater (lesser) fractal dimension [
is related to the integer derivatives. On the other hand, it has been established that the fractional derivative (fractional integral) of the Weierstrass function is another fractal function with a greater (lesser) fractal dimension [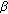 , with
, with  :
:
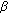 , with
, with 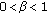 :
: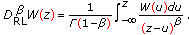
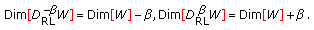
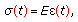
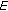 is Young's modulus,
is Young's modulus, 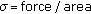 is the stress and
is the stress and 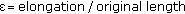 is the strain of the corresponding mechanical model, that, in this case, is represented by a spring characterized by the constant
is the strain of the corresponding mechanical model, that, in this case, is represented by a spring characterized by the constant 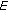 .
.
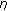 is the viscosity coefficient, and, in this case, the phenomenological model is represented by a dashpot.
is the viscosity coefficient, and, in this case, the phenomenological model is represented by a dashpot.
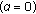 and Newton's law
and Newton's law  . This fractional relation can be realized physically through hierarchical arrangements and in the limit of an infinite number of springs and dashpots [
. This fractional relation can be realized physically through hierarchical arrangements and in the limit of an infinite number of springs and dashpots [

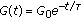 . From (4.7), we can write as starting point for the fractional generalization:
. From (4.7), we can write as starting point for the fractional generalization:
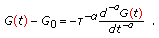
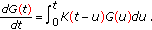
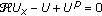 . Journal of Physics A 2000,33(38):6707-6720. 10.1088/0305-4470/33/38/305
. Journal of Physics A 2000,33(38):6707-6720. 10.1088/0305-4470/33/38/305