- Research Article
- Open access
- Published:
A Variational Inequality from Pricing Convertible Bond
Advances in Difference Equations volume 2011, Article number: 309678 (2011)
Abstract
The model of pricing American-style convertible bond is formulated as a zero-sum Dynkin game, which can be transformed into a parabolic variational inequality (PVI). The fundamental variable in this model is the stock price of the firm which issued the bond, and the differential operator in PVI is linear. The optimal call and conversion strategies correspond to the free boundaries of PVI. Some properties of the free boundaries are studied in this paper. We show that the bondholder should convert the bond if and only if the price of the stock is equal to a fixed value, and the firm should call the bond back if and only if the price is equal to a strictly decreasing function of time. Moreover, we prove that the free boundaries are smooth and bounded. Eventually we give some numerical results.
1. Introduction
Firms raise capital by issuing debt (bonds) and equity (shares of stock). The convertible bond is intermediate between these two instruments, which entitles its owner to receive coupons plus the return of principle at maturity. However, prior to maturity, the holder may convert the bond into the stock of the firm, surrendering it for a preset number of shares of stock. On the other hand, prior to maturity, the firm may call the bond forcing the bondholder to either surrender it to the firm for a previously agreed price or convert it into stock as before.
After issuing a convertible bond, the bondholder will find a proper time to exercise the conversion option in order to maximize the value of the bond, and the firm will choose its optimal time to exercise its call option to maximize the value of shareholder's equity. This situation was called "two-person" game (see [1, 2]). Because the firm must pay coupons to the bondholder, it may call the bond if it can subsequently reissue a bond with a lower coupon rate. This happens as the firm's fortunes improve, then the risk of default has diminished and investors will accept a lower coupon rate on the firm's bonds.
In [2] the authors assume that a firm's value is comprised of one equity and one convertible bond, the value of the issuing firm has constant volatility, the bond continuously pays coupons at a fixed rate, and the firm continuously pays dividends at a rate that is a fixed fraction of equity. Default occurs if the coupon payments cause the firm's value to fall to zero, in which case the bond has zero value. In their model, both the bond price and the stock price are functions of the underlying of the firm value. Because the stock price is the difference between firm value and bond price and dividends are paid proportionally to the stock price, a nonlinear differential equation was established for describing the bond price as a function of the firm value and time.
As we know, it is difficult to obtain the value of the firm. However, it is easier to get its stock price. So we choose the bond price  as a function of the stock price
as a function of the stock price  of the firm and time
of the firm and time  (see Chapter 36 in [3] or [4–7]).
(see Chapter 36 in [3] or [4–7]).
In Section 2, we formulate the model and deduce that  in the domain
in the domain  and
and  is governed by the following variational inequality in the domain
is governed by the following variational inequality in the domain  :
:

where  ,
,  ,
,  , and
, and  are positive constants.
are positive constants.  is the coupon rate,
is the coupon rate,  is the conversion ratio for converting the bond into the stock of the firm,
is the conversion ratio for converting the bond into the stock of the firm,  is the call price of the firm,
is the call price of the firm,  is the face value of the bond with
is the face value of the bond with  , and
, and  is just B-S operator (see [8]),
is just B-S operator (see [8]),

where  ,
,  , and
, and  are positive constants and represent the risk-free interest rate, the volatility, and the dividend rate of the firm stock, respectively. In this paper, we suppose that
are positive constants and represent the risk-free interest rate, the volatility, and the dividend rate of the firm stock, respectively. In this paper, we suppose that  and
and  . From a financial point of view, the assumption provides a possibility of calling the bond back from the firm (see Section 2 or [2]). Furthermore, we suppose that
. From a financial point of view, the assumption provides a possibility of calling the bond back from the firm (see Section 2 or [2]). Furthermore, we suppose that  . Otherwise, the firm should call the bond back before maturity and the value
. Otherwise, the firm should call the bond back before maturity and the value  makes no sense (see Section 2). It is clear that
makes no sense (see Section 2). It is clear that  is the unique solution if
is the unique solution if  . So we only consider the problem in the case of
. So we only consider the problem in the case of  .
.
Since (1.1) is a degenerate backward problem, we transform it into a familiar forward nondegenerate parabolic variational inequality problem; so letting

we have that

where

There are many papers on the convertible bond, such as [1, 2, 9]. But as we know, there are seldom results on the properties of the free boundaries—the optimal call and conversion strategies in the existing literature. The main aim of this paper is to analyze some properties of the free boundaries.
The pricing model of the convertible bond without call is considered in [9], where there exist two domains: the continuation domain CT and the conversion domain CV. The free boundary  between CT and CV means the optimal conversion strategy, which is dependent on the time
between CT and CV means the optimal conversion strategy, which is dependent on the time  and more than
and more than  .
.
But in this model, their exist three domains: the continuation domain CT, the callable domain CL, and the conversion domain  . The boundary between CV and
. The boundary between CV and  is
is  , which means the call strategy. The free boundary
, which means the call strategy. The free boundary  is the curve between CT and CL (see Figure 1), which means the optimal call strategy. And there exist
is the curve between CT and CL (see Figure 1), which means the optimal call strategy. And there exist  such that
such that

and  is strictly decreasing in
is strictly decreasing in  .
.
It means that the bondholder should convert the bond if and only if the stock price  of the firm is no less than
of the firm is no less than  , whereas, in the model without call, the bondholder may not convert the bond even if
, whereas, in the model without call, the bondholder may not convert the bond even if  . More precisely, the optimal conversion strategy
. More precisely, the optimal conversion strategy  without call is more than that
without call is more than that  in this paper (see [9] or Section 2). When the time to the expiry date is more than
in this paper (see [9] or Section 2). When the time to the expiry date is more than  , the firm should call the bond back if
, the firm should call the bond back if  . Neither the bondholder nor the firm should exercise their option if the time to the expiry date is less than
. Neither the bondholder nor the firm should exercise their option if the time to the expiry date is less than  and
and  . Moreover, when the time to the maturity lies in
. Moreover, when the time to the maturity lies in  , the bondholder should call the bond back if
, the bondholder should call the bond back if  .
.
In Section 2, we formulate and simplify the model. In Section 3, we will prove the existence and uniqueness of the strong solution of the parabolic variational inequality (1.4) and establish some estimations, which are important to analyze the property of the free boundary.
In Section 4, we show some behaviors of the free boundary  , such as its starting point and monotonicity. Particularly, we obtain the regularity of the free boundary
, such as its starting point and monotonicity. Particularly, we obtain the regularity of the free boundary  . As we know, the proof of the smoothness is trivial by the method in [10] if the difference between
. As we know, the proof of the smoothness is trivial by the method in [10] if the difference between  and the upper obstacle
and the upper obstacle  is decreasing with respect to
is decreasing with respect to  . But the proof is difficult if the condition is false (see [11–14]). In this problem,
. But the proof is difficult if the condition is false (see [11–14]). In this problem,  , which does not match the condition. Moreover,
, which does not match the condition. Moreover,  , and the starting point
, and the starting point  of the free boundary
of the free boundary  is not on the initial boundary, but the side boundary in this problem. Those make the proof of
is not on the initial boundary, but the side boundary in this problem. Those make the proof of  more complicated. The key idea is to construct cone locally containing the local free boundary and prove
more complicated. The key idea is to construct cone locally containing the local free boundary and prove  ; then the proof of
; then the proof of  is trivial. Moreover, we show that there is a lower bound
is trivial. Moreover, we show that there is a lower bound  of
of  and
and  converges to
converges to  as
as  converges to
converges to  in Theorem 4.4.
in Theorem 4.4.
In the last section, we provide numerical result applying the binomial method.
2. Formulation of the Model
In this section, we derive the mathematical model of pricing the convertible bond.
The firm issues the convertible bond, and the bondholder buys the bond. The firm has an obligation to continuously serve the coupon payment to the bondholder at the rate of  . In the life time of the bond, the bondholder has the right to convert it into the firm's stock with the conversion factor
. In the life time of the bond, the bondholder has the right to convert it into the firm's stock with the conversion factor  and obtains
and obtains  from the firm after converting, and the firm can call it back at a preset price of
from the firm after converting, and the firm can call it back at a preset price of  . The bondholder's right is superior to the firm's, which means that the bondholder has the right to convert the bond, but the firm has no right to call it if both sides hope to exercise their rights at the same time. If neither the bondholder nor the firm exercises their right before maturity, the bondholder must sell the bond to the firm at a preset value
. The bondholder's right is superior to the firm's, which means that the bondholder has the right to convert the bond, but the firm has no right to call it if both sides hope to exercise their rights at the same time. If neither the bondholder nor the firm exercises their right before maturity, the bondholder must sell the bond to the firm at a preset value  or convert it into the firm's stock at expiry date. So, the bondholder receives
or convert it into the firm's stock at expiry date. So, the bondholder receives  from the firm at maturity. It is reasonable that both of them wish to maximize the values of their respective holdings.
from the firm at maturity. It is reasonable that both of them wish to maximize the values of their respective holdings.
Suppose that under the risk neutral probability space  ; the stock price of the firm
; the stock price of the firm  follows
follows

where  ,
,  , and
, and  are positive constants, representing risk free interest rate, the dividend rate, and volatility of the stock, respectively.
are positive constants, representing risk free interest rate, the dividend rate, and volatility of the stock, respectively.  is a standard Brown motion on the probability space
is a standard Brown motion on the probability space  . Usually, the dividend rate
. Usually, the dividend rate  is smaller than the risk free interest rate
is smaller than the risk free interest rate  . So, we suppose that
. So, we suppose that  .
.
Denote by  the natural filtration generated by
the natural filtration generated by  and augmented by all the
and augmented by all the  -null sets in
-null sets in  . Let
. Let  be the set of all
be the set of all  -stopping times taking values in
-stopping times taking values in  .
.
The model can be expressed as a zero-sum Dynkin game. The payoff of the bondholder is

where  . The stopping time
. The stopping time  is the firm's strategy, and
is the firm's strategy, and  is the bondholder's strategy.
is the bondholder's strategy.
The bondholder chooses his strategy  to maximize
to maximize  ; meanwhile, the firm chooses its strategy
; meanwhile, the firm chooses its strategy  to minimize
to minimize  .
.
Denote the upper value  and the lower value
and the lower value  as
as

If  , then it is called the value of the Dynkin game and denoted as
, then it is called the value of the Dynkin game and denoted as  .
.
As we know, if the Dynkin game has a saddlepoint  , that is,
, that is,

then the value of the Dynkin game exists and

If  , then we deduce that, for any
, then we deduce that, for any  ,
,

So, in this case,  is a saddlepoint, and the value of the Dynkin game is
is a saddlepoint, and the value of the Dynkin game is

In the case of  , applying the standard method in [15], we see that the strong solution of the following variational inequality is the value of the Dynkin game:
, applying the standard method in [15], we see that the strong solution of the following variational inequality is the value of the Dynkin game:

If  , then the firm is bound to call the bond back before the maturity because the firm pays
, then the firm is bound to call the bond back before the maturity because the firm pays  after calling, but more than
after calling, but more than  without calling. In this case, the value
without calling. In this case, the value  makes no sense. So, we suppose that
makes no sense. So, we suppose that  .
.
If  , then the firm is bound to abandon its call right. From a financial point of view, the firm would pay
, then the firm is bound to abandon its call right. From a financial point of view, the firm would pay  to the bondholder at time
to the bondholder at time  after calling the bond, whereas, if the firm does not call in the time interval
after calling the bond, whereas, if the firm does not call in the time interval  , then he would pay the coupon payment
, then he would pay the coupon payment  and at most
and at most  of the face value of the convertible bond at time
of the face value of the convertible bond at time  . So, the discounted value of the bond without call is at most
. So, the discounted value of the bond without call is at most  . Hence, the firm should not call the bond back at time
. Hence, the firm should not call the bond back at time  .
.
From a stochastic point of view, we can denote a stopping time

If  ,
,  , then
, then  , and, for any
, and, for any  , we have
, we have

Moreover,  . So, for any
. So, for any  such that
such that  , it is clear that in the domain
, it is clear that in the domain 

which means that  is not the optimal call strategy, and the firm should not call in the domain
is not the optimal call strategy, and the firm should not call in the domain  .
.
From a variational inequality point of view, since

provided that  , which contradicts with the third inequality in (2.8), so, if
, which contradicts with the third inequality in (2.8), so, if  , then
, then  in the domain
in the domain  .
.
To remain the call strategy, we suppose that  . We will consider the other case in another paper because the two problems are fully different.
. We will consider the other case in another paper because the two problems are fully different.
Since we suppose that  and
and  , then
, then

Hence,  is empty in problem (2.8). So, problem (2.8) is reduced into problem (1.1).
is empty in problem (2.8). So, problem (2.8) is reduced into problem (1.1).
The model of pricing the bond without call is an optimal stopping problem

It is clear that

Since  , then
, then

where CV* is the conversion domain in the model without call and CV is that in this paper.
3. The Existence and Uniqueness of  Solution of Problem (1.4)
Solution of Problem (1.4)
Since problem (1.4) lies in the unbounded domain  , we need the following problem in the bounded domain
, we need the following problem in the bounded domain  to approximate to problem (1.4):
to approximate to problem (1.4):

where  and
and  .
.
Following the idea in [10, 16], we construct a penalty function  (see Figure 2), which satisfies
(see Figure 2), which satisfies

Consider the following penalty problem of (3.1):

where  is a smoothing function because the initial value
is a smoothing function because the initial value  is not smooth. It satisfies (see Figure 3)
is not smooth. It satisfies (see Figure 3)

Lemma 3.1.
For any fixed  , problem (3.3) has a unique solution
, problem (3.3) has a unique solution  for any
for any  and
and


Proof.
We apply the Schauder fixed point theorem [17] to prove the existence of nonlinear problem (3.3).
Denote  and
and  . Then
. Then  is a closed convex set in
is a closed convex set in  . Defining a mapping
. Defining a mapping  by
by  is the solution of the following linear problem:
is the solution of the following linear problem:

Furthermore, we can compute

where  is the parabolic boundary of
is the parabolic boundary of  . Thus
. Thus  is a supersolution of the problem (3.7), and
is a supersolution of the problem (3.7), and  . Hence
. Hence  . On the other hand,
. On the other hand,

which is bounded for fixed  . So, it is not difficult to prove that
. So, it is not difficult to prove that  is compact in
is compact in  and
and  is continuous. Owing to the Schauder fixed point theorem, we know that problem (3.3) has a solution
is continuous. Owing to the Schauder fixed point theorem, we know that problem (3.3) has a solution  . The proof of the uniqueness follows by the comparison principle. Here, we omit the details.
. The proof of the uniqueness follows by the comparison principle. Here, we omit the details.
Now, we prove (3.5). Since

Therefore,  is a supersolution of problem (3.3), and
is a supersolution of problem (3.3), and  in
in  . Moreover,
. Moreover,

Hence,  is a subsolution of problem (3.3). On the other hand,
is a subsolution of problem (3.3). On the other hand,

Thus,  is a subsolution of problem (3.3) as well, and we deduce
is a subsolution of problem (3.3) as well, and we deduce  .
.
In the following, we prove (3.6).
Indeed,  and
and  imply that
imply that  . Furthermore,
. Furthermore,  and
and  that imply
that imply  . Differentiating (3.3) with respect to
. Differentiating (3.3) with respect to  and denoting
and denoting  , we obtain
, we obtain

Then the comparison principle implies (3.6).
Theorem 3.2.
For any fixed  ,
,  , problem (3.1) admits a unique solution
, problem (3.1) admits a unique solution  for any
for any  , where
, where  ,
,  . Moreover, if
. Moreover, if  is large enough, one has that
is large enough, one has that



Proof.
From (3.5) and the properties of  , we have that
, we have that

By  and
and  (
( ) estimates of the parabolic problem [18], we conclude that
) estimates of the parabolic problem [18], we conclude that

where  is independent of
is independent of  . It implies that there exists a
. It implies that there exists a  and a subsequence of
and a subsequence of  (still denoted by
(still denoted by  ), such that as
), such that as  ,
,

Employing the method in [16] or [19], it is not difficult to derive that  is the solution of problem (3.1). And (3.14), (3.15) are the consequence of (3.5), (3.6) as
is the solution of problem (3.1). And (3.14), (3.15) are the consequence of (3.5), (3.6) as  .
.
In the following, we will prove (3.16). For any small  ,
,  satisfies, by (3.1),
satisfies, by (3.1),

Applying the comparison principle with respect to the initial value of the variational inequality (see [16]), we obtain

Thus (3.16) follows.
At last, we prove the uniqueness of the solution. Suppose that  and
and  are two
are two  solutions to problem (3.1), and denote
solutions to problem (3.1), and denote

Assume that  is not empty, and then, in the domain
is not empty, and then, in the domain  ,
,

Denoting  , we have that
, we have that

Applying the A-B-P maximum principle (see [20]), we have that  in
in  , which contradicts the definition of
, which contradicts the definition of  .
.
Theorem 3.3.
Problem (1.4) has a unique solution  for any
for any  ,
,  , and
, and  . And
. And  . Moreover,
. Moreover,



Proof.
Rewrite Problem (3.1) as follows:

where  implies that
implies that  and
and

where  denotes the indicator function of the set
denotes the indicator function of the set  .
.
Hence, for any fixed  , if
, if  , combining (3.14), we have the following
, combining (3.14), we have the following  and
and  uniform estimates [18]:
uniform estimates [18]:

here  depends on
depends on  and
and  depends on
depends on  , but they are independent of
, but they are independent of  . Then, we have that there is a
. Then, we have that there is a  and a subsequence of
and a subsequence of  (still denoted by
(still denoted by  ), such that for any
), such that for any  ,
,  ,
,

Moreover, (3.30) and imbedding theorem imply that

It is not difficult to deduce that  is the solution of problem (1.4). Furthermore, (3.32) implies that
is the solution of problem (1.4). Furthermore, (3.32) implies that  . And (3.25)–(3.27) are the consequence of (3.14)–(3.16). The proof of the uniqueness is similar to the proof in Theorem 3.2.
. And (3.25)–(3.27) are the consequence of (3.14)–(3.16). The proof of the uniqueness is similar to the proof in Theorem 3.2.
4. Behaviors of the Free Boundary
Denote

Thanks to (3.26), we can define the free boundary  of problem (1.4), at which it is optimal for the firm to call the bond, where
of problem (1.4), at which it is optimal for the firm to call the bond, where

(see Figure 1). It is clear that

Theorem 4.1.
Denote  . If
. If  , then
, then  , which means that
, which means that

Proof.
Define

We claim that  possess the following four properties:
possess the following four properties:
-
(i)
 ,
, -
(ii)
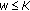 , for all
, for all 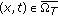 ,
, -
(iii)
 , for all
, for all  ,
, -
(iv)
 , a.e. in
, a.e. in  .
.
In fact, from the definition of  , we have that
, we have that

then property (i) is obvious.
Moreover, if  , then we deduce
, then we deduce

Combining  , we have property (ii). It is easy to check property (iii) from the definition of
, we have property (ii). It is easy to check property (iii) from the definition of  . Next, we manifest property (iv) according to the following two cases. In the case of
. Next, we manifest property (iv) according to the following two cases. In the case of  ,
,

In the other case of  ,
,

So, we testify properties (i)–(iv). In the following, we utilize the properties to prove  .
.
Otherwise,  is nonempty; then we have that
is nonempty; then we have that

Moreover,  on the parabolic boundary of
on the parabolic boundary of  . According to the A-B-P maximum principle (see [20]), we have that
. According to the A-B-P maximum principle (see [20]), we have that

which contradicts the definition of  . So, we achieve that
. So, we achieve that  .
.
Combining  for any
for any  , it is clear that
, it is clear that

which means that  ,
,  , and
, and  for any
for any 
Theorem 4.2.
The free boundary  is decreasing in the interval
is decreasing in the interval  . Moreover,
. Moreover,  . And
. And  .
.
Proof.
(3.26) and (3.27) imply that

Hence, for any unit vector  satisfying
satisfying  , the directional derivative of function
, the directional derivative of function  along
along  admits
admits

that is,  is increasing along the director
is increasing along the director  . Combining the condition
. Combining the condition  in
in  , we know that
, we know that  is monotonically decreasing. Hence,
is monotonically decreasing. Hence,  exists, and we can define
exists, and we can define

Since  , so
, so  . On the other hand, if
. On the other hand, if  , then
, then

It is impossible because  is continuous on
is continuous on  .
.
In the following, we prove that  is continuous in
is continuous in  . If it is false, then there exists
. If it is false, then there exists  ,
,  such that (see Figure 4)
such that (see Figure 4)

Moreover,

Differentiating (4.18) with respect to  , then
, then

On the other hand,  for any
for any  in this case, and we know that
in this case, and we know that  by (3.26). Applying the strong maximum principle to (4.19), we obtain
by (3.26). Applying the strong maximum principle to (4.19), we obtain

So, we can define  in
in  . Considering
. Considering  and
and  , we see that
, we see that  in
in  , which contradicts that
, which contradicts that  for any
for any  . Therefore
. Therefore  .
.
Theorem 4.3.
There exists some  such that
such that  for any
for any  and
and  is strictly decreasing on
is strictly decreasing on  .
.
Proof.
Define  . In the first, we prove that
. In the first, we prove that  . Otherwise,
. Otherwise,  and
and  for
for  .
.
Recalling the initial value, we see that

Meanwhile,  in the domain
in the domain  implies that
implies that  for any
for any  (see Figure 4); then
(see Figure 4); then  is not continuous at the point
is not continuous at the point  , which contradicts
, which contradicts  .
.
In the second, we prove that  . In fact, according to Lemma 3.1,
. In fact, according to Lemma 3.1,  for any
for any  , hence,
, hence,  . If
. If  , then the free boundary includes a horizontal line
, then the free boundary includes a horizontal line  ,
,  . Repeating the method in the proof of Theorem 4.2, then we can obtain a contradiction. So,
. Repeating the method in the proof of Theorem 4.2, then we can obtain a contradiction. So,  .
.
At last, we prove that  is strictly decreasing on
is strictly decreasing on  . Otherwise,
. Otherwise,  has a vertical part. Suppose that the vertical line is
has a vertical part. Suppose that the vertical line is  , then
, then  for any
for any  . Since
. Since  is continuous across the free boundary, then
is continuous across the free boundary, then  for any
for any  . In this case, we infer that
. In this case, we infer that

On the other hand, in the domain  ,
,  and
and  satisfy, respectively,
satisfy, respectively,

Then the strong maximum principle implies that  , which contradicts the second equality in (4.22).
, which contradicts the second equality in (4.22).
Theorem 4.4.
 for any
for any  with
with  (see Figure 1), where
(see Figure 1), where

where  is the positive characteristic root of
is the positive characteristic root of  , that is, the positive root of the algebraic equation
, that is, the positive root of the algebraic equation

Proof.
Define

We claim that  and possess the following three properties:
and possess the following three properties:
(i) for
for  and
and  for
for  ,
,
(ii) in
in  ,
,
(iii) in
in  .
.
In fact, if we notice that  , then we have that
, then we have that

It is obvious that  . So, we obtain property (i).
. So, we obtain property (i).
Moreover, we compute

Hence, we have property (ii).
It is not difficult to check that, for any  ,
,

Then we show property (iii).
Repeating the method in the proof of Theorem 3.2, we can derive that  in
in  from properties (i)-(ii). And property (iii) implies that
from properties (i)-(ii). And property (iii) implies that  in the domain
in the domain  , which means that
, which means that  for any
for any  .
.
Next, we prove that  . Otherwise,
. Otherwise,  ; then the free boundary includes a horizontal line
; then the free boundary includes a horizontal line  ,
,  . Repeating the method in the proof of Theorem 4.2, then we can obtain a contradiction. So,
. Repeating the method in the proof of Theorem 4.2, then we can obtain a contradiction. So,  .
.
Theorem 4.5.
The free boundary  .
.
Proof.
Fix  and
and  , and denote
, and denote  . According to Theorem 4.4, the free boundary
. According to Theorem 4.4, the free boundary  while
while  lies in the domain
lies in the domain  (see Figure 5).
(see Figure 5).
In the first, we prove that there exists an  such that
such that

In fact,  satisfy the equations
satisfy the equations

then the interior estimate of the parabolic equation implies that there exists a positive constant  such that
such that

here

On the other hand, we see that  in
in  from (3.27), and
from (3.27), and  . Applying the strong maximum principle to
. Applying the strong maximum principle to  , we deduce that
, we deduce that

It means that  is strictly decreasing on
is strictly decreasing on  . It follows that, by
. It follows that, by  ,
,

Moreover,

Employing the strong maximum principle, we see that there is a  , such that
, such that

Provided that  is small enough. Combining (4.32), there exists a positive
is small enough. Combining (4.32), there exists a positive  such that
such that

Next, we concentrate on problem (1.4) in the domain  . It is clear that
. It is clear that  satisfies
satisfies

And we can use the following problem to approximate the above problem:

Recalling (4.38), we see that, if  is small enough,
is small enough,  on the parabolic boundary of
on the parabolic boundary of  . Moreover,
. Moreover,  satisfies
satisfies

Applying the comparison principle, we obtain

As the method in the proof of Theorem 3.3, we can show that  weakly converges to
weakly converges to  in
in  and (4.30) is obvious.
and (4.30) is obvious.
On the other hand, we see that  in
in  for any positive number
for any positive number  from (3.26) and (3.27). So,
from (3.26) and (3.27). So,

which means that there exists a uniform cone such that the free boundary should lies in the cone. As the method in [9], it is easy to derive that  . Moreover
. Moreover  can be deduced by the bootstrap method. Since
can be deduced by the bootstrap method. Since  is arbitrary and the free boundary is a vertical line while
is arbitrary and the free boundary is a vertical line while  , then
, then  .
.
5. Numerical Results
Applying the binomial tree method to problem (1.4), we achieve the following numerical results—Figure 6:
Plot of the optimal exercise boundary  is a function of
is a function of  . The parameter values used in the calculations are
. The parameter values used in the calculations are  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  . In this case, the free boundary is increasing with
. In this case, the free boundary is increasing with  . The numerical result is coincided with that of our proof (see Figure 6).
. The numerical result is coincided with that of our proof (see Figure 6).
References
Sîrbu M, Pikovsky I, Shreve SE: Perpetual convertible bonds. SIAM Journal on Control and Optimization 2004,43(1):58-85. 10.1137/S0363012902412458
Sîrbu M, Shreve SE: A two-person game for pricing convertible bonds. SIAM Journal on Control and Optimization 2006,45(4):1508-1539. 10.1137/050630222
Wilmott P: Derivatives, the Theory and Practice of Financial Engineering. John Wiley & Sons, New York, NY, USA; 1998.
Kifer Y: Game options. Finance and Stochastics 2000,4(4):443-463. 10.1007/PL00013527
Kifer Y: Error estimates for binomial approximations of game options. The Annals of Applied Probability 2006,16(2):984-1033. 10.1214/105051606000000088
Kühn C, Kyprianou AE: Callable puts as composite exotic options. Mathematical Finance 2007,17(4):487-502. 10.1111/j.1467-9965.2007.00313.x
Kyprianou AE: Some calculations for Israeli options. Finance and Stochastics 2004,8(1):73-86. 10.1007/s00780-003-0104-5
Black F, Scholes M: The pricing of options and coperate liabilities. Journal of Political Economy 1973, 81: 637-659. 10.1086/260062
Yang Z, Yi F: A free boundary problem arising from pricing convertible bond. Applicable Analysis 2010,89(3):307-323. 10.1080/00036810903517563
Friedman A: Parabolic variational inequalities in one space dimension and smoothness of the free boundary. Journal of Functional Analysis 1975, 18: 151-176. 10.1016/0022-1236(75)90022-1
Blanchet A: On the regularity of the free boundary in the parabolic obstacle problem. Application to American options. Nonlinear Analysis: Theory, Methods & Applications 2006,65(7):1362-1378. 10.1016/j.na.2005.10.009
Blanchet A, Dolbeault J, Monneau R: On the continuity of the time derivative of the solution to the parabolic obstacle problem with variable coefficients. Journal de Mathématiques Pures et Appliquées. Neuvième Série 2006,85(3):371-414.
Caffarelli L, Petrosyan A, Shahgholian H: Regularity of a free boundary in parabolic potential theory. Journal of the American Mathematical Society 2004,17(4):827-869. 10.1090/S0894-0347-04-00466-7
Petrosyan A, Shahgholian H: Parabolic obstacle problems applied to finance. In Recent Developments in Nonlinear Partial Differential Equations, Contemporary Mathematics. Volume 439. American Mathematical Society, Providence, RI, USA; 2007:117-133.
Friedman A: Stochastic games and variational inequalities. Archive for Rational Mechanics and Analysis 1973, 51: 321-346.
Friedman A: Variational Principles and Free-Boundary Problems, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1982:ix+710.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Grundlehren der Mathematischen Wissenschaften. Volume 224. 2nd edition. Springer, Berlin, Germany; 1983:xiii+513.
Ladyženskaja OA, Solonnikov VA, Uralceva NN: Linear and Quasi-linear Equations of Parabolic Type. American Mathematical Society, Providence, RI, USA; 1968:736.
Yi F, Yang Z, Wang X: A variational inequality arising from European installment call options pricing. SIAM Journal on Mathematical Analysis 2008,40(1):306-326. 10.1137/060670353
Tso K: On Aleksandrov, Bakel'man type maximum principle for second order parabolic equations. Communications in Partial Differential Equations 1985,10(5):543-553. 10.1080/03605308508820388
Acknowledgments
The project is supported by NNSF of China (nos. 10971073, 10901060, and 11071085) and NNSF of Guang Dong province (no. 9451063101002091).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yan, H., Yi, F. A Variational Inequality from Pricing Convertible Bond. Adv Differ Equ 2011, 309678 (2011). https://doi.org/10.1155/2011/309678
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/309678

 .
. Solution of Problem (1.4)
Solution of Problem (1.4)
 .
.
 .
. ,
,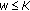 , for all
, for all 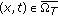 ,
, , for all
, for all  ,
, , a.e. in
, a.e. in  .
.
 .
.
 .
.