- Research Article
- Open access
- Published:
Some Results on  -Times Integrated
-Times Integrated  -Regularized Semigroups
-Regularized Semigroups
Advances in Difference Equations volume 2011, Article number: 394584 (2011)
Abstract
We present a generation theorem of  -times integrated
-times integrated  -regularized semigroups and clarify the relation between differentiable
-regularized semigroups and clarify the relation between differentiable  -times integrated
-times integrated  -regularized semigroups and singular
-regularized semigroups and singular  -times integrated
-times integrated  -regularized semigroups.
-regularized semigroups.
1. Introduction and Preliminaries
In 1987, Arendt [1] studied the  -times integrated semigroups, which are more general than
-times integrated semigroups, which are more general than  semigroups (there exist many operators that generate
semigroups (there exist many operators that generate  -times integrated semigroups but not
-times integrated semigroups but not  semigroups).
semigroups).
In recent years, the  -times integrated
-times integrated  -regularized semigroups have received much attention because they can be used to deal with ill-posed abstract Cauchy problems and characterize the "weak" well-posedness of many important differential equations (cf., e.g., [2–18]).
-regularized semigroups have received much attention because they can be used to deal with ill-posed abstract Cauchy problems and characterize the "weak" well-posedness of many important differential equations (cf., e.g., [2–18]).
Stimulated by the works in [2, 5–7, 9, 12–18], in this paper, we present a generation theorem of the  -times integrated
-times integrated  -regularized semigroups for the case that the domain of generator and the range of regularizing operator
-regularized semigroups for the case that the domain of generator and the range of regularizing operator  are not necessarily dense, and prove that the subgenerator of an exponentially bounded, differentiable
are not necessarily dense, and prove that the subgenerator of an exponentially bounded, differentiable  -times integrated
-times integrated  -regularized semigroup is also a subgenerator of a singular
-regularized semigroup is also a subgenerator of a singular  -times integrated
-times integrated  -regularized semigroup.
-regularized semigroup.
Throughout this paper,  is a Banach space;
is a Banach space;  denotes the dual space of
denotes the dual space of  ;
;  denotes the space of all linear and bounded operators from
denotes the space of all linear and bounded operators from  to
to  , it will be abbreviated to
, it will be abbreviated to  ;
;  denotes the dual space of
denotes the dual space of  . By
. By  we denote the space of all continuously differentiable
we denote the space of all continuously differentiable  -valued functions on
-valued functions on  .
.  is the space of all continuous
is the space of all continuous  -valued functions on
-valued functions on  .
.
All operators are linear. For a closed linear operator  , we write
, we write  ,
,  ,
,  for the domain, the range, the resolvent set of
for the domain, the range, the resolvent set of  in a Banach space
in a Banach space  , respectively.
, respectively.
We denote by  the part of
the part of  in
in  , that is,
, that is,

The  -resolvent set of
-resolvent set of  is defined as:
is defined as:

We abbreviate  -times integrated
-times integrated  -regularized semigroup to
-regularized semigroup to  -times integrated
-times integrated  -semigroup.
-semigroup.
Definition 1.1.
Let  be a nonnegative integer. Then
be a nonnegative integer. Then  is the subgenerator of an exponentially bounded
is the subgenerator of an exponentially bounded  -times integrated
-times integrated  -semigroup
-semigroup  if
if  for some
for some  and there exists a strongly continuous family
and there exists a strongly continuous family  with
with  for some
for some  such that
such that

In this case,  is called the exponentially bounded
is called the exponentially bounded  -times integrated
-times integrated  -semigroup generated by
-semigroup generated by  .
.
If  (resp.,
(resp.,  ), then
), then  is called a generator of an exponentially bounded
is called a generator of an exponentially bounded  -times integrated semigroup (resp.,
-times integrated semigroup (resp.,  -semigroup).
-semigroup).
We recall some properties of  -times integrated
-times integrated  -semigroup.
-semigroup.
Lemma 1.2 (see [10, Lemma 3.2]).
Assume that  is a subgenerator of an
is a subgenerator of an  -times integrated
-times integrated  -semigroup
-semigroup  . Then
. Then
-
(i)
 ,
, -
(ii)
 , and
, and  ,
, -
(iii)
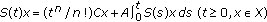 .
.
In particular,  .
.
Definition 1.3.
Let  . If
. If  and there exists
and there exists  such that
such that
-
(i)
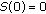 and
and  is strongly continuous,
is strongly continuous, -
(ii)
for
 ,
, 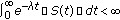 ,
, -
(iii)
 ,
,  ,
,  ,
,
then we say that  is a singular
is a singular  -times integrated
-times integrated  -semigroup with subgenerator
-semigroup with subgenerator  .
.
Remark 1.4.
Clearly, an exponentially bounded  -times integrated
-times integrated  -semigroup is a singular
-semigroup is a singular  -times integrated
-times integrated  -semigroup. But the converse is not true.
-semigroup. But the converse is not true.
2. The Main Results
Theorem 2.1.
Let  ,
,  be constants, and let
be constants, and let  be a closed operator satisfying
be a closed operator satisfying  . Assume that
. Assume that  is the nonnegative measurable function on
is the nonnegative measurable function on  . A necessary and sufficient condition for
. A necessary and sufficient condition for  is the subgenerator of an
is the subgenerator of an  -times integrated
-times integrated  -semigroup
-semigroup  satisfying
satisfying
-
(A1)
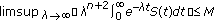 ,
, -
(A2)
 ,
,  , is that for
, is that for 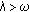 ,
,-
(i)
 ,
, -
(ii)
 ,
,  .
.
-
(i)
Proof.
Sufficiency. Let  . Set
. Set

For  , we have
, we have

Using this fact together with Widder's classical theorem, it is not difficult to see that the existence of a measurable function  with
with  , a.e., (
, a.e., ( ) such that
) such that

Let  ,
,  ,
,  . In view of the convolution theorem for Laplace transforms and from (2.3), we have
. In view of the convolution theorem for Laplace transforms and from (2.3), we have

Using the uniqueness of Laplace transforms and the linearity of  for each
for each  ,
,  , we can see that for each
, we can see that for each  ,
,  is linear and
is linear and

Hence for all  , there exists
, there exists  such that
such that



Denote by  the quotient mapping. Since
the quotient mapping. Since  , we deduce
, we deduce

It follows from the uniqueness theorem for Laplace transforms that  , that is,
, that is,  .
.
Combining (2.7) and (2.8) yields that  is strongly continuous and
is strongly continuous and

Now, we conclude that  is an
is an  -times integrated
-times integrated  -semigroup satisfying (A2). Assertion (A1) is immediate, by (2.8) and (i).
-semigroup satisfying (A2). Assertion (A1) is immediate, by (2.8) and (i).
Necessity.
Let  . Since
. Since  is an
is an  -times integrated
-times integrated  -semigroup on
-semigroup on  , we have
, we have

for  . Noting that
. Noting that  and
and  , we find
, we find

Then for any  and
and  , we obtain
, we obtain

Therefore, there exists a measurable function  on
on  with
with  (a.e.) such that
(a.e.) such that

Furthermore, by calculation, we have

Assertion (i) is an immediate consequence of (2.11) and (A1).
Remark 2.2.
If  and
and  , then
, then  is an integrated semigroup in the sense of Bobrowski [2].
is an integrated semigroup in the sense of Bobrowski [2].
Theorem 2.3.
Let  ,
,  be constants, and let
be constants, and let  be a closed operator satisfying
be a closed operator satisfying  . Assume that
. Assume that  is a subgenerator of an
is a subgenerator of an  -times integrated
-times integrated  -semigroup
-semigroup  and satisfies (ii) of Theorem 2.1 and
and satisfies (ii) of Theorem 2.1 and  . If
. If  is a subgenerator of an n-times integrated
is a subgenerator of an n-times integrated  -semigroup
-semigroup  on
on  , then for
, then for  ,
,  ,
,


Proof.
For  ,
,  , set
, set  as follows:
as follows:

Since  is strongly continuous on
is strongly continuous on  ,
,  is strongly continuous on
is strongly continuous on  .
.
Fixing  , we have
, we have

It follows from the uniqueness of Laplace transforms that  ,
,  . So we get (2.16). By the hypothesis
. So we get (2.16). By the hypothesis  , we see
, we see

and the proof is completed.
Now, we study the relation between differentiable  -times integrated
-times integrated  -semigroups and singular
-semigroups and singular  -times integrated
-times integrated  -semigroups.
-semigroups.
Theorem 2.4.
Let  , and let
, and let  be a closed operator satisfying
be a closed operator satisfying  . Assume that
. Assume that  is the nonnegative measurable function on
is the nonnegative measurable function on  . The following two assertions are equivalent:
. The following two assertions are equivalent:
-
(1)
 is the subgenerator of a singular
is the subgenerator of a singular  -times integrated
-times integrated 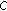 -semigroup
-semigroup 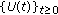 satisfying
satisfying  .
. -
(2)
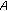 is the subgenerator of an exponentially bounded
is the subgenerator of an exponentially bounded  -times integrated
-times integrated  -semigroup
-semigroup  satisfying
satisfying (2.21)
(2.21)Proof.
(1)⇒(2): we set

Since  is locally integrable on
is locally integrable on  is well-defined for any
is well-defined for any  . It is easy to check that
. It is easy to check that  belongs to
belongs to  .
.
For every  , since
, since

we deduce that  is exponentially bounded.
is exponentially bounded.
Moreover, for  , we have
, we have

Thus  is the desired semigroup in (2).
is the desired semigroup in (2).
(2)⇒(1): for any  , we set
, we set

Then  and
and  .
.
Noting that

we find

Since  is continuously differentiable for
is continuously differentiable for  , we get
, we get

Moreover, for  , we have
, we have

Thus,  is a singular
is a singular  -times integrated
-times integrated  -semigroup with subgenerator
-semigroup with subgenerator  .
.
Theorem 2.5.
Let  ,
,  be constants, and let
be constants, and let  be a closed operator satisfying
be a closed operator satisfying  . Let
. Let  be the function in Theorem 2.4. If
be the function in Theorem 2.4. If  is the subgenerator of a singular
is the subgenerator of a singular  -times integrated
-times integrated  -semigroup
-semigroup  , satisfying
, satisfying  , and satisfies
, and satisfies

then
-
(1)
for
 ,
,  ,
, 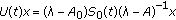 ,
, -
(2)
for
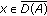 ,
,  ,
, -
(3)
for
 ,
,  ,
, 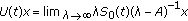 ,
, -
(4)
for
 ,
,  if and only if
if and only if  ,
,
where  and
and  are the symbols mentioned in Theorem 2.3.
are the symbols mentioned in Theorem 2.3.
Proof.
It follows from Theorems 2.3 and 2.4 that  subgenerates an
subgenerates an  -times integrated
-times integrated  -semigroup
-semigroup  , which is continuously differentiable for
, which is continuously differentiable for  and satisfies (2.16) and (2.17).
and satisfies (2.16) and (2.17).
Differentiating (2.16) with respect to  , we obtain
, we obtain

This completes the proof of (1).
To show (2), for  , we have
, we have

Letting  , we get
, we get

To show (3), for  , since
, since  , it follows from (2.17) that
, it follows from (2.17) that  is continuous for
is continuous for  , thus, we have
, thus, we have

Obviously, the equality above is true for  .
.
Noting that

we can deduce that  implies
implies  , and from
, and from

assertion (4) is immediate if we note that  implies
implies  .
.
References
Arendt W: Vector-valued Laplace transforms and Cauchy problems. Israel Journal of Mathematics 1987,59(3):327-352. 10.1007/BF02774144
Bobrowski A: On the generation of non-continuous semigroups. Semigroup Forum 1997,54(2):237-252.
Li Y-C, Shaw S-Y:On local
 -times integrated
-times integrated 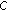 -semigroups. Abstract and Applied Analysis 2007, 2007:-18.
-semigroups. Abstract and Applied Analysis 2007, 2007:-18.Li Y-C, Shaw S-Y:On characterization and perturbation of local
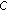 -semigroups. Proceedings of the American Mathematical Society 2007,135(4):1097-1106. 10.1090/S0002-9939-06-08549-2
-semigroups. Proceedings of the American Mathematical Society 2007,135(4):1097-1106. 10.1090/S0002-9939-06-08549-2Liang J, Xiao T-J: Integrated semigroups and higher order abstract equations. Journal of Mathematical Analysis and Applications 1998,222(1):110-125. 10.1006/jmaa.1997.5909
Liang J, Xiao T-J: Wellposedness results for certain classes of higher order abstract Cauchy problems connected with integrated semigroups. Semigroup Forum 1998,56(1):84-103. 10.1007/s00233-002-7007-1
Liang J, Xiao T-J:Norm continuity for
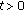 of linear operator families. Chinese Science Bulletin 1998,43(9):719-723. 10.1007/BF02898945
of linear operator families. Chinese Science Bulletin 1998,43(9):719-723. 10.1007/BF02898945Nagaoka K: Generation of the integrated semigroups by superelliptic differential operators. Journal of Mathematical Analysis and Applications 2008,341(2):1143-1154. 10.1016/j.jmaa.2007.10.045
Tanaka N: Locally Lipschitz continuous integrated semigroups. Studia Mathematica 2005,167(1):1-16. 10.4064/sm167-1-1
Thieme HR: "Integrated semigroups" and integrated solutions to abstract Cauchy problems. Journal of Mathematical Analysis and Applications 1990,152(2):416-447. 10.1016/0022-247X(90)90074-P
Thieme HR: Differentiability of convolutions, integrated semigroups of bounded semi-variation, and the inhomogeneous Cauchy problem. Journal of Evolution Equations 2008,8(2):283-305. 10.1007/s00028-007-0355-2
Xiao T-J, Liang J: Integrated semigroups, cosine families and higher order abstract Cauchy problems. In Functional Analysis in China, Mathematics and Its Applications. Volume 356. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:351-365.
Xiao T-J, Liang J: Widder-Arendt theorem and integrated semigroups in locally convex space. Science in China. Series A 1996,39(11):1121-1130.
Xiao T-J, Liang J: Laplace transforms and integrated, regularized semigroups in locally convex spaces. Journal of Functional Analysis 1997,148(2):448-479. 10.1006/jfan.1996.3096
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Approximations of Laplace transforms and integrated semigroups. Journal of Functional Analysis 2000,172(1):202-220. 10.1006/jfan.1999.3545
Xiao T-J, Liang J: Higher order abstract Cauchy problems: their existence and uniqueness families. Journal of the London Mathematical Society 2003,67(1):149-164. 10.1112/S0024610702003794
Xiao T-J, Liang J: Second order differential operators with Feller-Wentzell type boundary conditions. Journal of Functional Analysis 2008,254(6):1467-1486. 10.1016/j.jfa.2007.12.012
Acknowledgments
The authors are grateful to the referees for their valuable suggestions. This work is supported by the NSF of Yunnan Province (2009ZC054M).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, F., Wang, H. & Qu, Z. Some Results on  -Times Integrated
-Times Integrated  -Regularized Semigroups.
Adv Differ Equ 2011, 394584 (2011). https://doi.org/10.1155/2011/394584
-Regularized Semigroups.
Adv Differ Equ 2011, 394584 (2011). https://doi.org/10.1155/2011/394584
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/394584
 ,
, , and
, and  ,
,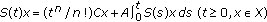 .
.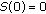 and
and  is strongly continuous,
is strongly continuous, ,
, 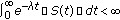 ,
, ,
,  ,
,  ,
,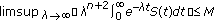 ,
, ,
,  , is that for
, is that for 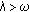 ,
, ,
, ,
,  .
. is the subgenerator of a singular
is the subgenerator of a singular  -times integrated
-times integrated 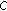 -semigroup
-semigroup 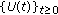 satisfying
satisfying  .
.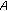 is the subgenerator of an exponentially bounded
is the subgenerator of an exponentially bounded  -times integrated
-times integrated  -semigroup
-semigroup  satisfying
satisfying
 ,
,  ,
, 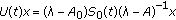 ,
,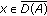 ,
,  ,
, ,
,  ,
, 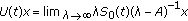 ,
, ,
,  if and only if
if and only if  ,
, -times integrated
-times integrated 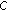 -semigroups. Abstract and Applied Analysis 2007, 2007:-18.
-semigroups. Abstract and Applied Analysis 2007, 2007:-18.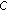 -semigroups. Proceedings of the American Mathematical Society 2007,135(4):1097-1106. 10.1090/S0002-9939-06-08549-2
-semigroups. Proceedings of the American Mathematical Society 2007,135(4):1097-1106. 10.1090/S0002-9939-06-08549-2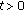 of linear operator families. Chinese Science Bulletin 1998,43(9):719-723. 10.1007/BF02898945
of linear operator families. Chinese Science Bulletin 1998,43(9):719-723. 10.1007/BF02898945