- Review Article
- Open access
- Published:
On the Generalized  -Genocchi Numbers and Polynomials of Higher-Order
-Genocchi Numbers and Polynomials of Higher-Order
Advances in Difference Equations volume 2011, Article number: 424809 (2011)
Abstract
We first consider the  -extension of the generating function for the higher-order generalized Genocchi numbers and polynomials attached to
-extension of the generating function for the higher-order generalized Genocchi numbers and polynomials attached to  . The purpose of this paper is to present a systemic study of some families of higher-order generalized
. The purpose of this paper is to present a systemic study of some families of higher-order generalized  -Genocchi numbers and polynomials attached to
-Genocchi numbers and polynomials attached to  by using the generating function of those numbers and polynomials.
by using the generating function of those numbers and polynomials.
1. Introduction
As a well known definition, the Genocchi polynomials are defined by

where we use the technical method's notation by replacing  by
by  , symbolically, (see [1, 2]). In the special case
, symbolically, (see [1, 2]). In the special case  ,
,  are called the
are called the  th Genocchi numbers. From the definition of Genocchi numbers, we note that
th Genocchi numbers. From the definition of Genocchi numbers, we note that  , and even coefficients are given by
, and even coefficients are given by  (see [3]), where
(see [3]), where  is a Bernoulli number and
is a Bernoulli number and  is an Euler polynomial. The first few Genocchi numbers for
is an Euler polynomial. The first few Genocchi numbers for  are
are  . The first few prime Genocchi numbers are given by
. The first few prime Genocchi numbers are given by  and
and  . It is known that there are no other prime Genocchi numbers with
. It is known that there are no other prime Genocchi numbers with  . For a real or complex parameter
. For a real or complex parameter  , the higher-order Genocchi polynomials are defined by
, the higher-order Genocchi polynomials are defined by

(see [1, 4]). In the special case  ,
,  are called the
are called the  th Genocchi numbers of order
th Genocchi numbers of order  . From (1.1) and (1.2), we note that
. From (1.1) and (1.2), we note that  . For
. For  with
with  , let
, let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . It is known that the generalized Genocchi polynomials attached to
. It is known that the generalized Genocchi polynomials attached to  are defined by
are defined by

(see [1]). In the special case  ,
,  are called the
are called the  th generalized Genocchi numbers attached to
th generalized Genocchi numbers attached to  (see [1, 4–6]).
(see [1, 4–6]).
For a real or complex parameter  , the generalized higher-order Genocchi polynomials attached to
, the generalized higher-order Genocchi polynomials attached to  are also defined by
are also defined by

(see [7]). In the special case  ,
,  are called the
are called the  th generalized Genocchi numbers attached to
th generalized Genocchi numbers attached to  of order
of order  (see [1, 4–9]). From (1.3) and (1.4), we derive
(see [1, 4–9]). From (1.3) and (1.4), we derive  .
.
Let us assume that  with
with  as an indeterminate. Then we, use the notation
as an indeterminate. Then we, use the notation

The  -factorial is defined by
-factorial is defined by

and the Gaussian binomial coefficient is also defined by


It is known that

(see [5, 10]). The  -binomial formula are known that
-binomial formula are known that

There is an unexpected connection with  -analysis and quantum groups, and thus with noncommutative geometry
-analysis and quantum groups, and thus with noncommutative geometry  -analysis is a sort of
-analysis is a sort of  -deformation of the ordinary analysis. Spherical functions on quantum groups are
-deformation of the ordinary analysis. Spherical functions on quantum groups are  -special functions. Recently, many authors have studied the
-special functions. Recently, many authors have studied the  -extension in various areas (see [1–15]). Govil and Gupta [10] have introduced a new type of
-extension in various areas (see [1–15]). Govil and Gupta [10] have introduced a new type of  -integrated Meyer-König-Zeller-Durrmeyer operators, and their results are closely related to the study of
-integrated Meyer-König-Zeller-Durrmeyer operators, and their results are closely related to the study of  -Bernstein polynomials and
-Bernstein polynomials and  -Genocchi polynomials, which are treated in this paper. In this paper, we first consider the
-Genocchi polynomials, which are treated in this paper. In this paper, we first consider the  -extension of the generating function for the higher-order generalized Genocchi numbers and polynomials attached to
-extension of the generating function for the higher-order generalized Genocchi numbers and polynomials attached to  . The purpose of this paper is to present a systemic study of some families of higher-order generalized
. The purpose of this paper is to present a systemic study of some families of higher-order generalized  -Genocchi numbers and polynomials attached to
-Genocchi numbers and polynomials attached to  by using the generating function of those numbers and polynomials.
by using the generating function of those numbers and polynomials.
2. Generalized 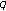 -Genocchi Numbers and Polynomials
-Genocchi Numbers and Polynomials
For  , let us consider the
, let us consider the  -extension of the generalized Genocchi polynomials of order
-extension of the generalized Genocchi polynomials of order  attached to
attached to  as follows:
as follows:

Note that

By (2.1) and (1.4), we can see that  . From (2.1), we note that
. From (2.1), we note that

In the special case  ,
,  are called the
are called the  th generalized
th generalized  -Genocchi numbers of order
-Genocchi numbers of order  attached to
attached to  . Therefore, we obtain the following theorem.
. Therefore, we obtain the following theorem.
Theorem 2.1.
For  , one has
, one has

Note that

Thus we obtain the following corollary.
Corollary 2.2.
For  , we have
, we have

For  and
and  , one also considers the extended higher-order generalized
, one also considers the extended higher-order generalized  -Genocchi polynomials as follows:
-Genocchi polynomials as follows:

From (2.7), one notes that

where  .
.
Therefore, we obtain the following theorem.
Theorem 2.3.
For  , one has
, one has

Note that

By (2.10), one sees that

By (2.10) and (2.11), we obtain the following corollary.
Corollary 2.4.
For  , we have
, we have

By (2.7), we can derive the following corollary.
Corollary 2.5.
For  with
with  , we have
, we have

For  in Theorem 2.3, we obtain the following corollary.
in Theorem 2.3, we obtain the following corollary.
Corollary 2.6.
For  , one has
, one has

In particular,

Let  in Corollary 2.6. Then one has
in Corollary 2.6. Then one has

Let  . Then, one has defines Barnes' type generalized
. Then, one has defines Barnes' type generalized  -Genocchi polynomials attached to
-Genocchi polynomials attached to  as follows:
as follows:

By (2.17), one sees that

It is easy to see that

Therefore, we obtain the following theorem.
Theorem 2.7.
For  , one has
, one has

References
Jang L-C, Hwang K-W, Kim Y-H:A note on
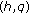 -Genocchi polynomials and numbers of higher order. Advances in Difference Equations 2010, 2010:-6.
-Genocchi polynomials and numbers of higher order. Advances in Difference Equations 2010, 2010:-6.Kurt V: A further symmetric relation on the analogue of the Apostol-Bernoulli and the analogue of the Apostol-Genocchi polynomials. Applied Mathematical Sciences 2009,3(53–56):2757-2764.
Kim T:On the
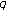 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037Jang L-C:A study on the distribution of twisted
 -Genocchi polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,18(2):181-189.
-Genocchi polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,18(2):181-189.Kim T: Some identities for the Bernoulli, the Euler and the Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2010,20(1):23-28.
Kim T:A note on the
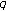 -Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.
-Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.Rim S-H, Lee SJ, Moon EJ, Jin JH:On the
 -Genocchi numbers and polynomials associated with
-Genocchi numbers and polynomials associated with  -zeta function. Proceedings of the Jangjeon Mathematical Society 2009,12(3):261-267.
-zeta function. Proceedings of the Jangjeon Mathematical Society 2009,12(3):261-267.Rim S-H, Park KH, Moon EJ: On Genocchi numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-7.
Ryoo CS: Calculating zeros of the twisted Genocchi polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2008,17(2):147-159.
Govil NK, Gupta V:Convergence of
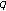 -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):97-108.
-Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):97-108.Kim T:Barnes-type multiple
 -zeta functions and
-zeta functions and 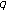 -Euler polynomials. Journal of Physics 2010,43(25):-11.
-Euler polynomials. Journal of Physics 2010,43(25):-11.Cangul IN, Kurt V, Ozden H, Simsek Y:On the higher-order
 -
-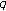 -Genocchi numbers. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):39-57.
-Genocchi numbers. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):39-57.Kim T:On the multiple
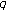 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055Kim T:Note on the Euler
 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007Cenkci M, Can M, Kurt V:
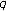 -extensions of Genocchi numbers. Journal of the Korean Mathematical Society 2006,43(1):183-198.
-extensions of Genocchi numbers. Journal of the Korean Mathematical Society 2006,43(1):183-198.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ryoo, C., Kim, T., Choi, J. et al. On the Generalized  -Genocchi Numbers and Polynomials of Higher-Order.
Adv Differ Equ 2011, 424809 (2011). https://doi.org/10.1155/2011/424809
-Genocchi Numbers and Polynomials of Higher-Order.
Adv Differ Equ 2011, 424809 (2011). https://doi.org/10.1155/2011/424809
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/424809
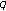 -Genocchi Numbers and Polynomials
-Genocchi Numbers and Polynomials -Genocchi polynomials and numbers of higher order. Advances in Difference Equations 2010, 2010:-6.
-Genocchi polynomials and numbers of higher order. Advances in Difference Equations 2010, 2010:-6. -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037 -Genocchi polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,18(2):181-189.
-Genocchi polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,18(2):181-189.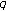 -Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.
-Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8. -Genocchi numbers and polynomials associated with
-Genocchi numbers and polynomials associated with  -zeta function. Proceedings of the Jangjeon Mathematical Society 2009,12(3):261-267.
-zeta function. Proceedings of the Jangjeon Mathematical Society 2009,12(3):261-267.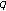 -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):97-108.
-Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):97-108. -zeta functions and
-zeta functions and 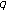 -Euler polynomials. Journal of Physics 2010,43(25):-11.
-Euler polynomials. Journal of Physics 2010,43(25):-11. -
-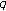 -Genocchi numbers. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):39-57.
-Genocchi numbers. Advanced Studies in Contemporary Mathematics (Kyungshang) 2009,19(1):39-57. -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007 -extensions of Genocchi numbers. Journal of the Korean Mathematical Society 2006,43(1):183-198.
-extensions of Genocchi numbers. Journal of the Korean Mathematical Society 2006,43(1):183-198.