- Research Article
- Open access
- Published:
 -Stability of Impulsive Neural Networks with Unbounded Time-Varying Delays and Continuously Distributed Delays
-Stability of Impulsive Neural Networks with Unbounded Time-Varying Delays and Continuously Distributed Delays
Advances in Difference Equations volume 2011, Article number: 437842 (2011)
Abstract
This paper is concerned with the problem of  -stability of impulsive neural systems with unbounded time-varying delays and continuously distributed delays. Some
-stability of impulsive neural systems with unbounded time-varying delays and continuously distributed delays. Some  -stability criteria are derived by using the Lyapunov-Krasovskii functional method. Those criteria are expressed in the form of linear matrix inequalities (LMIs), and they can easily be checked. A numerical example is provided to demonstrate the effectiveness of the obtained results.
-stability criteria are derived by using the Lyapunov-Krasovskii functional method. Those criteria are expressed in the form of linear matrix inequalities (LMIs), and they can easily be checked. A numerical example is provided to demonstrate the effectiveness of the obtained results.
1. Introduction
In recent years, the dynamics of neural networks have been extensively studied because of their application in many areas, such as associative memory, pattern recognition, and optimization [1–4]. Many researchers have a lot of contributions to these subjects. Stability is a basic knowledge for dynamical systems and is useful to the real-life systems. The time delays happen frequently in various engineering, biological, and economical systems, and they may cause instability and poor performance of practical systems. Therefore, the stability analysis for neural networks with time-delay has attracted a large amount of research interest, and many sufficient conditions have been proposed to guarantee the stability of neural networks with various type of time delays, see for example [5–20] and the references therein. However, most of the results are obtained based on the assumption that the time delay is bounded. As we know, time delays occur and vary frequently and irregularly in many engineering systems, and sometimes they depend on the histories heavily and may be unbounded [21, 22]. In such case, those existing results in [5–20] are all invalid.
How to guarantee the desirable stability if the time delays are unbounded? Recently, Chen et al. [23, 24] proposed a new concept of  -stability and established some sufficient conditions to guarantee the global
-stability and established some sufficient conditions to guarantee the global  -stability of delayed neural networks with or without uncertainties via different approaches. Those results can be applied to neural networks with unbounded time-varying delays. Moreover, few results have been reported in the literature concerning the problem of
-stability of delayed neural networks with or without uncertainties via different approaches. Those results can be applied to neural networks with unbounded time-varying delays. Moreover, few results have been reported in the literature concerning the problem of  -stability of impulsive neural networks with unbounded time-varying delays and continuously distributed delays. As we know, the impulse phenomenon as well as time delays are ubiquitous in the real world [25–27]. The systems with impulses and time delays can describe the real world well and truly. This inspire our interests.
-stability of impulsive neural networks with unbounded time-varying delays and continuously distributed delays. As we know, the impulse phenomenon as well as time delays are ubiquitous in the real world [25–27]. The systems with impulses and time delays can describe the real world well and truly. This inspire our interests.
In this paper, we investigate the problem of  -stability for a class of impulsive neural networks with unbounded time-varying delays and continuously distributed delays. Based on Lyapunov-Krasovskii functional and some analysis techniques, several sufficient conditions that ensure the
-stability for a class of impulsive neural networks with unbounded time-varying delays and continuously distributed delays. Based on Lyapunov-Krasovskii functional and some analysis techniques, several sufficient conditions that ensure the  -stability of the addressed systems are derived in terms of LMIs, which can easily be checked by resorting to available software packages. The organization of this paper is as follows. The problems investigated in the paper are formulated, and some preliminaries are presented, in Section 2. In Section 3, we state and prove our main results. Then, a numerical example is given to demonstrate the effectiveness of the obtained results in Section 4. Finally, concluding remarks are made in Section 5.
-stability of the addressed systems are derived in terms of LMIs, which can easily be checked by resorting to available software packages. The organization of this paper is as follows. The problems investigated in the paper are formulated, and some preliminaries are presented, in Section 2. In Section 3, we state and prove our main results. Then, a numerical example is given to demonstrate the effectiveness of the obtained results in Section 4. Finally, concluding remarks are made in Section 5.
2. Preliminaries
Notations
Let  denote the set of real numbers,
denote the set of real numbers,  denote the set of positive integers, and
denote the set of positive integers, and  denote the
denote the  -dimensional real spaces equipped with the Euclidean norm
-dimensional real spaces equipped with the Euclidean norm  . Let
. Let  or
or  denote that the matrix
denote that the matrix  is a symmetric and positive semidefinite or negative semidefinite matrix. The notations
is a symmetric and positive semidefinite or negative semidefinite matrix. The notations  and
and  mean the transpose of
mean the transpose of  and the inverse of a square matrix.
and the inverse of a square matrix.  or
or  denote the maximum eigenvalue or the minimum eigenvalue of matrix
denote the maximum eigenvalue or the minimum eigenvalue of matrix  denotes the identity matrix with appropriate dimensions and
denotes the identity matrix with appropriate dimensions and  . In addition, the notation
. In addition, the notation  always denotes the symmetric block in one symmetric matrix.
always denotes the symmetric block in one symmetric matrix.
Consider the following impulsive neural networks with time delays:

where the impulse times  satisfy
satisfy  is the neuron state vector of the neural network;
is the neuron state vector of the neural network;  is a diagonal matrix with
is a diagonal matrix with  are the connection weight matrix, the delayed weight matrix, and the distributively delayed connection weight matrix, respectively;
are the connection weight matrix, the delayed weight matrix, and the distributively delayed connection weight matrix, respectively;  is an input constant vector;
is an input constant vector;  is the transmission delay of the neural networks;
is the transmission delay of the neural networks;  represents the neuron activation function;
represents the neuron activation function;  is the delay kernel function and
is the delay kernel function and  is the impulsive function.
is the impulsive function.
Throughout this paper, the following assumptions are needed.
-
(H1)
The neuron activation functions
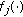 ,
,  , are bounded and satisfy
, are bounded and satisfy (22)
(22)for any
 ,
,  . Moreover, we define
. Moreover, we define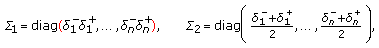 (23)
(23)where
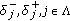 are some real constants and they may be positive, zero, or negative.
are some real constants and they may be positive, zero, or negative. -
(H2)
The delay kernels
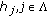 , are some real value nonnegative continuous functions defined in
, are some real value nonnegative continuous functions defined in 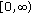 and satisfy
and satisfy (24)
(24) -
(H3)
 is a nonnegative and continuously differentiable time-varying delay and satisfies
is a nonnegative and continuously differentiable time-varying delay and satisfies 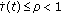 , where
, where 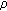 is a positive constant.
is a positive constant.
If the function  satisfies the hypotheses (H1) above, there exists an equilibrium point for system (2.1), see [28]. Assume that
satisfies the hypotheses (H1) above, there exists an equilibrium point for system (2.1), see [28]. Assume that  is an equilibrium of system (2.1) and the impulsive function in system (2.1) characterized by
is an equilibrium of system (2.1) and the impulsive function in system (2.1) characterized by  , where
, where  is a real matrix. Then, one can derive from (2.1) that the transformation
is a real matrix. Then, one can derive from (2.1) that the transformation  transforms system (2.1) into the following system:
transforms system (2.1) into the following system:

where  .
.
Obviously, the  -stability analysis of the equilibrium point
-stability analysis of the equilibrium point  of system (2.1) can be transformed to the
of system (2.1) can be transformed to the  -stability analysis of the trivial solution
-stability analysis of the trivial solution  of system (2.5). For completeness, we first give the following definition and lemmas.
of system (2.5). For completeness, we first give the following definition and lemmas.
Definition 2.1 (see [23]).
Suppose that  is a nonnegative continuous function and satisfies
is a nonnegative continuous function and satisfies  as
as  . If there exists a scalar
. If there exists a scalar  such that
such that

then the system (2.1) is said to be  -stable.
-stable.
Obviously, the definition of  -stable includes the global asymptotical and the global exponential stability.
-stable includes the global asymptotical and the global exponential stability.
Lemma 2.2 (see [29]).
For a given matrix

where  , is equivalent to any one of the following conditions:
, is equivalent to any one of the following conditions:
-
(1)
 ;
; -
(2)
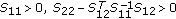 .
.
3. Main Results
Theorem 3.1.
Assume that assumptions (H1), (H2), and (H3) hold. Then, the zero solution of system (2.5) is  -stable if there exist some constants
-stable if there exist some constants  , two
, two  matrices
matrices  , two diagonal positive definite
, two diagonal positive definite  matrices
matrices  , a nonnegative continuous differential function
, a nonnegative continuous differential function  defined on
defined on  , and a constant
, and a constant  such that, for
such that, for 

and the following LMIs hold:

where  .
.
Proof.
Consider the Lyapunov-Krasovskii functional:

The time derivative of  along the trajectories of system (2.5) can be derived as
along the trajectories of system (2.5) can be derived as

It follows from the assumption (3.1) that

We use the assumption (H2) and Cauchy's inequality  and get
and get

Note that, for any  diagonal matrix
diagonal matrix  it follows that
it follows that

Substituting (3.5), (3.6) and (3.7), to (3.4), we get, for  ,
,

where

So, by assumption (3.2) and (3.8), we have

In addition, we note that

which, together with assumption (3.2) and Lemma 2.2, implies that

Thus, it yields

Hence, we can deduce that

By (3.10) and (3.14), we know that  is monotonically nonincreasing for
is monotonically nonincreasing for  , which implies that
, which implies that

It follows from the definition of  that
that

where  .
.
It implies that

This completes the proof of Theorem 3.1.
Remark 3.2.
Theorem 3.1 provides a  -stability criterion for an impulsive differential system (2.5). It should be noted that the conditions in the theorem are dependent on the upper bound of the derivative of time-varying delay and the delay kernels
-stability criterion for an impulsive differential system (2.5). It should be noted that the conditions in the theorem are dependent on the upper bound of the derivative of time-varying delay and the delay kernels  , and independent of the range of time-varying delay. Thus, it can be applied to impulsive neural networks with unbounded time-varying and continuously distributed delays.
, and independent of the range of time-varying delay. Thus, it can be applied to impulsive neural networks with unbounded time-varying and continuously distributed delays.
Remark 3.3.
In [23, 24], the authors have studied  -stability for neural networks with unbounded time-varying delays and continuously distributed delays via different approaches. However, the impulsive effect is not taken into account. Hence, our developed result in this paper complements and improves those reported in [23, 24]. In particular, if we take
-stability for neural networks with unbounded time-varying delays and continuously distributed delays via different approaches. However, the impulsive effect is not taken into account. Hence, our developed result in this paper complements and improves those reported in [23, 24]. In particular, if we take  ,
, ,
,  , then the following result can be obtained.
, then the following result can be obtained.
Corollary 3.4.
Assume that assumptions (H1), (H2) and (H3) hold. Then, the zero solution of system (2.5) is  -stable if there exist some constants
-stable if there exist some constants  ,
,  ,
,  ,
,  , two
, two  matrices
matrices  ,
,  , two diagonal positive definite
, two diagonal positive definite  matrices
matrices  ,
,  , a nonnegative continuous differential function
, a nonnegative continuous differential function  defined on
defined on  , and a constant
, and a constant  such that, for
such that, for 

and the following LMIs hold:

where  ,
,  .
.
If we take  (
( denotes a constant), then the following global bounded result can be obtained.
denotes a constant), then the following global bounded result can be obtained.
Corollary 3.5.
Assume that assumptions (H1), (H2), and (H3) hold. Then, the all solutions of system (2.5) have global boundedness if there exist two  matrices
matrices  ,
,  , two diagonal positive definite
, two diagonal positive definite  matrices
matrices  ,
, , such that, the following LMIs hold:
, such that, the following LMIs hold:

where  .
.
Remark 3.6.
Notice that  ,
,  ,
,  ,
,  , and using the similar proof of Theorem 3.1, we can obtain the result easily.
, and using the similar proof of Theorem 3.1, we can obtain the result easily.
4. A Numerical Example
In the following, we give an example to illustrate the validity of our method.
Example 4.1.
Consider a two-dimensional impulsive neural network with unbounded time-varying delays and continuously distributed delays:

Then,  ,
,  ,
,  ,
,  , and
, and  . It is obvious that
. It is obvious that  is an equilibrium point of system (4.1). Let
is an equilibrium point of system (4.1). Let  and choose
and choose  ,
,  ,
,  , then the LMIs in Theorem 3.1 have the following feasible solution via MATLAB LMI toolbox:
, then the LMIs in Theorem 3.1 have the following feasible solution via MATLAB LMI toolbox:

The above results shows that all the conditions stated in Theorem 3.1 have been satisfied and hence system (4.1) with unbounded time-varying delay and continuously distributed delay is  -stable. The numerical simulations are shown in Figure 1.
-stable. The numerical simulations are shown in Figure 1.
5. Conclusion
In this paper, some sufficient conditions for  -stability of impulsive neural networks with unbounded time-varying delays and continuously distributed delays are derived. The results are described in terms of LMIs, which can be easily checked by resorting to available software packages. A numerical example has been given to demonstrate the effectiveness of the results obtained.
-stability of impulsive neural networks with unbounded time-varying delays and continuously distributed delays are derived. The results are described in terms of LMIs, which can be easily checked by resorting to available software packages. A numerical example has been given to demonstrate the effectiveness of the results obtained.
References
Chua LO, Yang L: Cellular neural networks: theory. IEEE Transactions on Circuits and Systems 1988,35(10):1257-1272. 10.1109/31.7600
Cohen MA, Grossberg S: Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Transactions on Systems, Man, and Cybernetics 1983,13(5):815-826.
Hopfield JJ: Neurons with graded response have collective computational properties like those of two-state neurons. Proceedings of the National Academy of Sciences of the United States of America 1984,81(10 I):3088-3092.
Kosko B: Bidirectional associative memories. IEEE Transactions on Systems, Man, and Cybernetics 1988,18(1):49-60. 10.1109/21.87054
Zhang Q, Wei X, Xu J: Delay-dependent global stability results for delayed Hopfield neural networks. Chaos, Solitons & Fractals 2007,34(2):662-668. 10.1016/j.chaos.2006.03.073
Mohamad S, Gopalsamy K, Akça H: Exponential stability of artificial neural networks with distributed delays and large impulses. Nonlinear Analysis: Real World Applications 2008,9(3):872-888. 10.1016/j.nonrwa.2007.01.011
Wang Q, Liu X: Exponential stability of impulsive cellular neural networks with time delay via Lyapunov functionals. Applied Mathematics and Computation 2007,194(1):186-198. 10.1016/j.amc.2007.04.112
Huang Z-T, Yang Q-G, Luo X: Exponential stability of impulsive neural networks with time-varying delays. Chaos, Solitons & Fractals 2008,35(4):770-780. 10.1016/j.chaos.2006.05.089
Lou XY, Cui B: New LMI conditions for delay-dependent asymptotic stability of delayed Hopfield neural networks. Neurocomputing 2006,69(16–18):2374-2378.
Singh V: On global robust stability of interval Hopfield neural networks with delay. Chaos, Solitons & Fractals 2007,33(4):1183-1188. 10.1016/j.chaos.2006.01.121
Arik S: Global asymptotic stability of hybrid bidirectional associative memory neural networks with time delays. Physics Letters, Section A 2006,351(1-2):85-91. 10.1016/j.physleta.2005.10.059
Zhang Y, Sun J: Stability of impulsive neural networks with time delays. Physics Letters, Section A 2005,348(1-2):44-50. 10.1016/j.physleta.2005.08.030
Liao X, Li C: An LMI approach to asymptotical stability of multi-delayed neural networks. Physica D 2005,200(1-2):139-155. 10.1016/j.physd.2004.10.009
Mohamad S: Exponential stability in Hopfield-type neural networks with impulses. Chaos, Solitons & Fractals 2007,32(2):456-467. 10.1016/j.chaos.2006.06.035
Ou O: Global robust exponential stability of delayed neural networks: an LMI approach. Chaos, Solitons & Fractals 2007,32(5):1742-1748. 10.1016/j.chaos.2005.12.026
Rakkiyappan R, Balasubramaniam P, Cao J: Global exponential stability results for neutral-type impulsive neural networks. Nonlinear Analysis: Real World Applications 2010,11(1):122-130. 10.1016/j.nonrwa.2008.10.050
Rakkiyappan R, Balasubramaniam P: On exponential stability results for fuzzy impulsive neural networks. Fuzzy Sets and Systems 2010,161(13):1823-1835. 10.1016/j.fss.2009.12.016
Raja R, Sakthivel R, Anthoni SM: Stability analysis for discrete-time stochastic neural networks with mixed time delays and impulsive effects. Canadian Journal of Physics 2010,88(12):885-898. 10.1139/P10-086
Sakthivel R, Samidurai R, Anthoni SM: New exponential stability criteria for stochastic BAM neural networks with impulses. Physica Scripta 2010.,82(4):
Sakthivel R, Samidurai R, Anthoni SM: Asymptotic stability of stochastic delayed recurrent neural networks with impulsive effects. Journal of Optimization Theory and Applications 2010,147(3):583-596. 10.1007/s10957-010-9728-8
Niculescu S-I: Delay Effects on Stability: A RobustControl Approach, Lecture Notes in Control and Information Sciences. Volume 269. Springer, London, UK; 2001:xvi+383.
Kolmanovskiĭ VB, Nosov VR: Stability of Functional Differential Equations, Mathematics in Science and Engineering. Volume 180. Academic Press, London, UK; 1986:xiv+217.
Chen T, Wang L: Global μ -stability of delayed neural networks with unbounded time-varying delays. IEEE Transactions on Neural Networks 2007,18(6):705-709.
Liu X, Chen T: Robust μ -stability for uncertain stochastic neural networks with unbounded time-varying delays. Physica A 2008,387(12):2952-2962.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Baĭnov DD, Simeonov PS: Systems with Impulse Effect: Stability Theory and Applications, Ellis Horwood Series: Mathematics and Its Applications. Ellis Horwood, Chichester, UK; 1989:255.
Li X: Uniform asymptotic stability and global stabiliy of impulsive infinite delay differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1975-1983. 10.1016/j.na.2008.02.096
Li X, Fu X, Balasubramaniam P, Rakkiyappan R: Existence, uniqueness and stability analysis of recurrent neural networks with time delay in the leakage term under impulsive perturbations. Nonlinear Analysis: Real World Applications 2010,11(5):4092-4108. 10.1016/j.nonrwa.2010.03.014
Boyd S, El Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory, SIAM Studies in Applied Mathematics. Volume 15. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, Pa, USA; 1994:xii+193.
Acknowledgments
This paper is supported by the National Natural Science Foundation of China (11071276), the Natural Science Foundation of Shandong Province (Y2008A29, ZR2010AL016), and the Science and Technology Programs of Shandong Province (2008GG30009008).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yin, L., Fu, X.
 -Stability of Impulsive Neural Networks with Unbounded Time-Varying Delays and Continuously Distributed Delays.
Adv Differ Equ 2011, 437842 (2011). https://doi.org/10.1155/2011/437842
-Stability of Impulsive Neural Networks with Unbounded Time-Varying Delays and Continuously Distributed Delays.
Adv Differ Equ 2011, 437842 (2011). https://doi.org/10.1155/2011/437842
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/437842
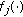 ,
,  , are bounded and satisfy
, are bounded and satisfy
 ,
,  . Moreover, we define
. Moreover, we define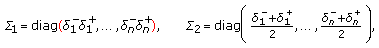
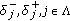 are some real constants and they may be positive, zero, or negative.
are some real constants and they may be positive, zero, or negative.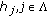 , are some real value nonnegative continuous functions defined in
, are some real value nonnegative continuous functions defined in 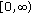 and satisfy
and satisfy
 is a nonnegative and continuously differentiable time-varying delay and satisfies
is a nonnegative and continuously differentiable time-varying delay and satisfies 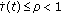 , where
, where 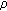 is a positive constant.
is a positive constant. ;
;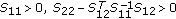 .
.