- Research Article
- Open access
- Published:
Nonlocal Cauchy Problem for Nonautonomous Fractional Evolution Equations
Advances in Difference Equations volume 2011, Article number: 483816 (2011)
Abstract
We investigate the mild solutions of a nonlocal Cauchy problem for nonautonomous fractional evolution equations  ,
,  , in Banach spaces, where
, in Banach spaces, where  ,
,  . New results are obtained by using Sadovskii's fixed point theorem and the Banach contraction mapping principle. An example is also given.
. New results are obtained by using Sadovskii's fixed point theorem and the Banach contraction mapping principle. An example is also given.
1. Introduction
During the past decades, the fractional differential equations have been proved to be valuable tools in the investigation of many phenomena in engineering and physics; they attracted many researchers (cf., e.g., [1–9]). On the other hand, the autonomous and nonautonomous evolution equations and related topics were studied in, for example, [6, 7, 10–20], and the nonlocal Cauchy problem was considered in, for example, [2, 5, 18, 21–26].
In this paper, we consider the following nonlocal Cauchy problem for nonautonomous fractional evolution equations

in Banach spaces, where  ,
,  . The terms
. The terms  ,
,  are defined by
are defined by

the positive functions  are continuous on
are continuous on  and
and

Let us assume that  and
and  is a family linear closed operator defined in a Banach space
is a family linear closed operator defined in a Banach space  . The fractional order integral of the function
. The fractional order integral of the function  is understood here in the Riemann-Liouville sense, that is,
is understood here in the Riemann-Liouville sense, that is,

In this paper, we denote that  is a positive constant and assume that a family of closed linear
is a positive constant and assume that a family of closed linear  satisfying
satisfying
(A1) the domain  of
of  is dense in the Banach space
is dense in the Banach space  and independent of
and independent of  ,
,
(A2) the operator  exists in
exists in  for any
for any  with
with  and
and

(A3) There exists constant  and
and  such that
such that

Under condition (A2), each operator  ,
,  generates an analytic semigroup
generates an analytic semigroup  ,
, , and there exists a constant
, and there exists a constant  such that
such that

where  ,
,  ,
,  ([11]).
([11]).
We study the existence of mild solution of (1.1) and obtain the existence theorem based on the measures of noncompactness. An example is given to show an application of the abstract results.
2. Preliminaries
Throughout this work, we set  . We denote by
. We denote by  a Banach space,
a Banach space,  the space of all linear and bounded operators on
the space of all linear and bounded operators on  , and
, and  the space of all
the space of all  -valued continuous functions on
-valued continuous functions on  .
.
Lemma 2.1 (see [9]).
-
(1)
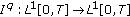 .
. -
(2)
For
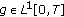 , we have
, we have  (2.1)
(2.1)
where  is a Beta function.
is a Beta function.
Definition 2.2.
Let  be a bounded set of seminormed linear space
be a bounded set of seminormed linear space  . The Kuratowski's measure of noncompactness (for brevity,
. The Kuratowski's measure of noncompactness (for brevity,  -measure) of
-measure) of  is defined as
is defined as

From the definition, we can get some properties of  -measure immediately, see ([27]).
-measure immediately, see ([27]).
Lemma 2.3 (see [27]).
Let  and
and  be bounded sets of
be bounded sets of  . Then
. Then
-
(1)
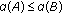 , if
, if 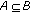 .
. -
(2)
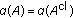 , where
, where  denotes the closure of
denotes the closure of 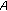 .
. -
(3)
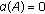 if and only if
if and only if  is precompact.
is precompact. -
(4)
 ,
, 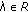 .
. -
(5)
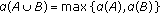 .
. -
(6)
 , where
, where  .
. -
(7)
 , for any
, for any  .
.
For  we define
we define

for  , where
, where  .
.
The following lemma will be needed.
Lemma 2.4 (see [27]).
If  is a bounded, equicontinuous set, then
is a bounded, equicontinuous set, then
-
(1)
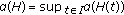 .
. -
(2)
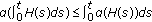 , for
, for 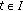 .
.
Lemma 2.5 (see [28]).
If  and there exists a
and there exists a  such that
such that

then  is integrable and
is integrable and

We need to use the following Sadovskii's fixed point theorem.
Definition 2.6 (see [29]).
Let  be an operator in Banach space
be an operator in Banach space  . If
. If  is continuous and takes bounded, sets into bounded sets, and
is continuous and takes bounded, sets into bounded sets, and  for every bounded set
for every bounded set  of
of  with
with  , then
, then  is said to be a condensing operator on
is said to be a condensing operator on  .
.
Lemma 2.7 (Sadovskii's fixed point theorem [29]).
Let  be a condensing operator on Banach space
be a condensing operator on Banach space  . If
. If  for a convex, closed, and bounded set
for a convex, closed, and bounded set  of
of  , then
, then  has a fixed point in
has a fixed point in  .
.
According to [4], a mild solution of (1.1) can be defined as follows.
Definition 2.8.
A function  satisfying the equation
satisfying the equation

is called a mild solution of (1.1), where

and  is a probability density function defined on
is a probability density function defined on  such that its Laplace transform is given by
such that its Laplace transform is given by

where

To our purpose, the following conclusions will be needed. For the proofs refer to [4].
Lemma 2.9 (see [4]).
The operator-valued functions  and
and  are continuous in uniform topology in the variables
are continuous in uniform topology in the variables  ,
,  , where
, where  ,
,  , for any
, for any  . Clearly,
. Clearly,

Moreover, we have

Remark 2.10.
From the proof of Theorem 2.5 in [4], we can see
-
(1)
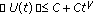 .
. -
(2)
For
 ,
, 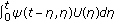 is uniformly continuous in the norm of
is uniformly continuous in the norm of 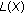 and
and  (2.12)
(2.12)
3. Existence of Solution
Assume that
(B1) satisfies
satisfies  is measurable for all
is measurable for all  ,
, and
and  is continuous for a.e
is continuous for a.e  , and there exist a positive function
, and there exist a positive function  and a continuous nondecreasing function
and a continuous nondecreasing function  such that
such that

and set  .
.
(B2) For any bounded sets  , and
, and  ,
,

where  is a nonnegative function, and
is a nonnegative function, and  ,
,

(B3) is continuous and there exists
is continuous and there exists

such that

(B4) The functions  and
and  satisfy the following condition:
satisfy the following condition:

where  , and
, and  .
.
Theorem 3.1.
Suppose that (B1)–(B4) are satisfied, and if  , then (1.1) has a mild solution on
, then (1.1) has a mild solution on  .
.
Proof.
Define the operator  by
by

Then we proceed in five steps.
Step 1.
We show that  is continuous.
is continuous.
Let  be a sequence that
be a sequence that  as
as  . Since
. Since  satisfies (B1), we have
satisfies (B1), we have

Then

According to the condition (A2), (2.12), and the continuity of  , we have
, we have

Noting that  in
in  , there exists
, there exists  such that
such that  for
for  sufficiently large. Therefore, we have
sufficiently large. Therefore, we have

Using (2.10) and by means of the Lebesgue dominated convergence theorem, we obtain

Similarly, by (2.10) and (2.11), we have

Therefore, we deduce that

Step 2.
We show that  maps bounded sets of
maps bounded sets of  into bounded sets in
into bounded sets in  .
.
For any  , we set
, we set  . Now, for
. Now, for  , by (B1), we can see
, by (B1), we can see

Based on (2.12), we denote that  , we have
, we have

Then for any  , by (A2), (2.10), (2.11), and Lemma 2.1, we have
, by (A2), (2.10), (2.11), and Lemma 2.1, we have

where  .
.
By means of the Hölder inequality, we have

Thus

This means  .
.
Step 3.
We show that there exists  such that
such that  .
.
Suppose the contrary, that for every  , there exists
, there exists  and
and  , such that
, such that  . However, on the other hand
. However, on the other hand

we have

Dividing both sides by  and taking the lower limit as
and taking the lower limit as  , we obtain
, we obtain

which contradicts (B4).
Step 4.
Denote

where

We show that  is equicontinuous.
is equicontinuous.
Let  and
and  . Then
. Then

where

It follows from Lemma 2.9, (B1), and (3.20) that  .
.
For  , from (2.10), (3.20), and (B1), we have
, from (2.10), (3.20), and (B1), we have

Similarly, by (2.10), (2.11), (B1), and Lemma 2.1, we have

Step 5.
We show that  for every bounded set
for every bounded set  . For any
. For any  , we can take a sequence
, we can take a sequence  such that
such that

(cf. [30]). So it follows from Lemmas 2.3–2.5, 2.9, (2) in Remark 2.10, and (B2) that

Since  is arbitrary, we can obtain
is arbitrary, we can obtain

In summary, we have proven that  has a fixed point
has a fixed point  . Consequently, (1.1) has at least one mild solution.
. Consequently, (1.1) has at least one mild solution.
Our next result is based on the Banach's fixed point theorem.
(G1) There exists a positive function  and a constant
and a constant  such that
such that

(G2) There exists a constant  such that the function
such that the function  defined by
defined by

Theorem 3.2.
Assume that (G1), (G2) are satisfied, then (1.1) has a unique mild solution.
Proof.
Let  be defined as in Theorem 3.1. For any
be defined as in Theorem 3.1. For any  , we have
, we have

Thus, from (A2), (2.10), (2.11), Lemma 2.1, we have

We get

By the Banach contraction mapping principle,  has a unique fixed point, which is a mild solution of (1.1).
has a unique fixed point, which is a mild solution of (1.1).
4. An Example
To illustrate the usefulness of our main result, we consider the following fractional differential equation:

where  ,
,  ,
,  ,
,  ,
,  is continuous function and is uniformly Hölder continuous in
is continuous function and is uniformly Hölder continuous in  , that is, there exist
, that is, there exist  and
and  such that
such that

Let  and define
and define  by
by

Then  generates an analytic semigroup
generates an analytic semigroup  .
.
For  ,
,  , we set
, we set

where

Moreover, we can get

for any  . Then the above equation (4.1) can be written in the abstract form as (1.1). On the other hand,
. Then the above equation (4.1) can be written in the abstract form as (1.1). On the other hand,

where  ,
,  satisfying (B1). For any
satisfying (B1). For any  ,
,

Therefore, for any bounded sets  , we have
, we have

Moreover,

Similarly, we obtain

Suppose further that
-
(1)
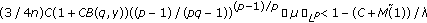 ,
, -
(2)
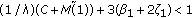 .
.
Then (4.1) has a mild solution by Theorem 3.1.
References
Agarwal RP, Belmekki M, Benchohra M: A survey on semilinear differential equations and inclusions involving Riemann-Liouville fractional derivative. Advances in Difference Equations 2009, 2009:-47.
Anguraj A, Karthikeyan P, N'Guérékata GM: Nonlocal Cauchy problem for some fractional abstract integro-differential equations in Banach spaces. Communications in Mathematical Analysis 2009,6(1):31-35.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons and Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: The fundamental solutions for fractional evolution equations of parabolic type. Journal of Applied Mathematics and Stochastic Analysis 2004, (3):197-211.
Li F: Mild solutions for fractional differential equations with nonlocal conditions. Advances in Difference Equations 2010, 2010:-9.
Li F: Solvability of nonautonomous fractional integrodifferential equations with infinite delay. Advances in Difference Equations 2011, 2011:-18.
Liang J, Xiao T-J: Solutions to nonautonomous abstract functional equations with infinite delay. Taiwanese Journal of Mathematics 2006,10(1):163-172.
Mophou GM: Existence and uniqueness of mild solutions to impulsive fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1604-1615. 10.1016/j.na.2009.08.046
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science, New York, NY, USA; 1993:xxxvi+976.
Diagana T: Pseudo-almost automorphic solutions to some classes of nonautonomous partial evolution equations. Differential Equations & Applications 2009,1(4):561-582.
Hille E, Phillips RS: Functional Analysis and Semi-Groups, American Mathematical Society Colloquium Publications. Volume 31. American Mathematical Society, Providence, RI, USA; 1957:xii+808.
Josić K, Rosenbaum R: Unstable solutions of nonautonomous linear differential equations. SIAM Review 2008,50(3):570-584. 10.1137/060677057
Kunze M, Lorenzi L, Lunardi A: Nonautonomous Kolmogorov parabolic equations with unbounded coefficients. Transactions of the American Mathematical Society 2010,362(1):169-198.
Liang J, Nagel R, Xiao T-J: Approximation theorems for the propagators of higher order abstract Cauchy problems. Transactions of the American Mathematical Society 2008,360(4):1723-1739.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Approximations of Laplace transforms and integrated semigroups. Journal of Functional Analysis 2000,172(1):202-220. 10.1006/jfan.1999.3545
Xiao T-J, Liang J: Existence of classical solutions to nonautonomous nonlocal parabolic problems. Nonlinear Analysis: Theory, Methods and Applications 2005,63(5–7):e225-e232.
Xiao T-J, Liang J: Second order differential operators with Feller-Wentzell type boundary conditions. Journal of Functional Analysis 2008,254(6):1467-1486. 10.1016/j.jfa.2007.12.012
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Byszewski L, Lakshmikantham V: Theorem about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space. Applicable Analysis 1991,40(1):11-19. 10.1080/00036819008839989
Fan Z: Impulsive problems for semilinear differential equations with nonlocal conditions. Nonlinear Analysis: Theory, Methods & Applications 2010,72(2):1104-1109. 10.1016/j.na.2009.07.049
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Liang J, van Casteren J, Xiao T-J: Nonlocal Cauchy problems for semilinear evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2002,50(2):173-189. 10.1016/S0362-546X(01)00743-X
Liu H, Chang J-C: Existence for a class of partial differential equations with nonlocal conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3076-3083. 10.1016/j.na.2008.04.009
Banaś J, Goebel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980:vi+97.
Heinz H-P: On the behaviour of measures of noncompactness with respect to differentiation and integration of vector-valued functions. Nonlinear Analysis: Theory, Methods & Applications 1983,7(12):1351-1371. 10.1016/0362-546X(83)90006-8
Sadovskii B: On a fixed point principle. Functional Analysis and Its Applications 1967, 2: 151-153.
Bothe D: Multivalued perturbations of m-accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiao, F. Nonlocal Cauchy Problem for Nonautonomous Fractional Evolution Equations. Adv Differ Equ 2011, 483816 (2011). https://doi.org/10.1155/2011/483816
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/483816
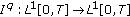 .
.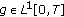 , we have
, we have 
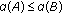 , if
, if 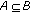 .
.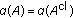 , where
, where  denotes the closure of
denotes the closure of 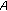 .
.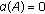 if and only if
if and only if  is precompact.
is precompact. ,
, 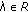 .
.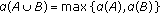 .
. , where
, where  .
. , for any
, for any  .
.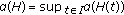 .
.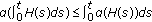 , for
, for 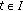 .
.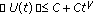 .
. ,
, 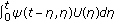 is uniformly continuous in the norm of
is uniformly continuous in the norm of 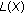 and
and 
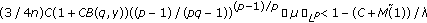 ,
,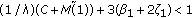 .
.