- Research Article
- Open access
- Published:
Positive Solutions of m-Point Boundary Value Problems for Fractional Differential Equations
Advances in Difference Equations volume 2011, Article number: 571804 (2011)
Abstract
We discuss the existence of minimal and maximal positive solutions for fractional differential equations with multipoint boundary value conditions, and new results are given. An example is also given to illustrate the abstract results.
1. Introduction
Recently, [1] discussed the existence of positive solutions for the following boundary value problem of fractional order differential equation

where  is the standard Riemann-Liouville fractional derivative of order
is the standard Riemann-Liouville fractional derivative of order  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  satisfies Carathéodory-type conditions. Moreover, [2] considered the following nonlinear
satisfies Carathéodory-type conditions. Moreover, [2] considered the following nonlinear  -point boundary value problem of fractional type:
-point boundary value problem of fractional type:

where  takes values in a reflexive Banach space
takes values in a reflexive Banach space  ,
,

 with
with  and
and  denotes the
denotes the  th Pseudo-derivative of
th Pseudo-derivative of  ,
,  denotes the Pseudo fractional differential operator of order
denotes the Pseudo fractional differential operator of order  ,
,  is a continuous real-valued function on
is a continuous real-valued function on  , and
, and  is a vector-valued Pettis-integrable function.
is a vector-valued Pettis-integrable function.
In this paper, we consider the existence of minimal and maximal positive solutions for the following multiple-point boundary value problem:

where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,

 ,
,  is continuous,
is continuous,  ,
,  ,
,  ,
,  ,
,  , and
, and

New results on the problem will be obtained.
Recall the following well-known definition and lemma (for more details on cone theory, see [3]).
Definition 1.1.
Let  be a real Banach space. Then,
be a real Banach space. Then,
-
(a)
a nonempty convex closed set
 is called a cone if it satisfied the following two conditions:
is called a cone if it satisfied the following two conditions: -
(i)
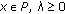 implies
implies 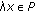 ,
, -
(ii)
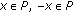 implies
implies 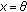 , where
, where 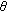 denotes the zero element of
denotes the zero element of 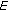 .
.
-
(b)
a cone
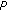 is said to be normal if there exists a constant
is said to be normal if there exists a constant 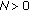 such that
such that 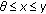 implies
implies 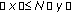 .
.
Lemma 1.2.
Assume that  with a fractional derivative of order
with a fractional derivative of order  that belongs to
that belongs to  . Then,
. Then,

where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to  .
.
2. Main Results
Let  and
and  . Then,
. Then,  is the Banach space endowed with the norm
is the Banach space endowed with the norm  and
and  is normal cone.
is normal cone.
We list the following assumptions to be used in this paper.
 there exist two nonnegative real-valued functions
there exist two nonnegative real-valued functions  , such that
, such that

 for
for  implies
implies  .
.
In the following, we will prove our main results.
Lemma 2.1.
Let  . Then, the fractional differential equation
. Then, the fractional differential equation

has a unique solution which is given by

where

in which

where

Proof.
Using Lemma 1.2, we have

It follows from the condition  that
that  .
.
Thus,

This, together with the relation  , yields
, yields

From the boundary value condition  , we deduce that
, we deduce that

Thus,

The proof is complete.
Lemma 2.2.
If  , then function
, then function  in Lemma 2.1 satisfies the following conditions:
in Lemma 2.1 satisfies the following conditions:
(i)  , for
, for  ,
,
(ii)  , for s,
, for s, ,
,
where

in which

Proof.
When  , we have
, we have

Thus,  for
for  .
.
Furthermore, we conclude that

So,  for
for  . This, together with
. This, together with  for
for  , yields
, yields  for
for  .
.
Observing the express of  ,
,  , and
, and  , we see that
, we see that  holds.
holds.
The proof is complete.
Remark 2.3.
From the express of  and
and  , we see that
, we see that

Thus,

Now, we define an operator  by
by

Theorem 2.4.
Let condition  be satisfied. Suppose that
be satisfied. Suppose that  . Then, problem (1.4) has at least one positive solution.
. Then, problem (1.4) has at least one positive solution.
Proof.
Let  , where
, where

Step 1.
 , for any
, for any 

which implies that  .
.
Step 2.
 is continuous.
is continuous.
It is obvious from  .
.
Step 3.
 is equicontinuous.
is equicontinuous.
From (2.11) and (2.18), for any  ,
,  ,
,  , we conclude that
, we conclude that

As  , the right-hand side of the above inequality tends to zero, so,
, the right-hand side of the above inequality tends to zero, so,  is equicontinuous.
is equicontinuous.
By the Arzelá-Ascoli theorem, we conclude that the operator  is completely continuous. Thus, our conclusion follows from Schauder fixed point theorem, and the proof is complete.
is completely continuous. Thus, our conclusion follows from Schauder fixed point theorem, and the proof is complete.
Theorem 2.5.
Besides the hypotheses of Theorem 2.4, we suppose that  holds. Then, BVP (1.4) has minimal positive solution
holds. Then, BVP (1.4) has minimal positive solution  in
in  and maximal positive solution
and maximal positive solution  in
in  ; Moreover,
; Moreover,  ,
,  as
as  uniformly on
uniformly on  , where
, where


Proof.
By Theorem 2.4, we know that BVP (1.4) has at least one positive solution in  .
.
Step 1.
BVP (1.4) has a positive solution in  , which is minimal positive solution.
, which is minimal positive solution.
From (2.18) and (2.22), one can see that

This, together with  , yields that
, yields that

From  and the proof of Theorem 2.4, it may be concluded that
and the proof of Theorem 2.4, it may be concluded that  and
and  .
.
Let

Thus,

By the complete community of  , we know that
, we know that  is relatively compact. So, there exists a
is relatively compact. So, there exists a  and a subsequence
and a subsequence

such that  converges to
converges to  uniformly on
uniformly on  . Since
. Since  is normal and
is normal and  is nondecreasing, it is easily seen that the entire sequence
is nondecreasing, it is easily seen that the entire sequence  converges to
converges to  uniformly on
uniformly on  .
.  being closed convex set in
being closed convex set in  and
and  imply that
imply that  .
.
From

and  , we see that
, we see that

By (2.30), (2.22), and Lebesgue's dominated convergence theorem, we get

Let  be any positive solution of BVP (1.4) in
be any positive solution of BVP (1.4) in  . It is obvious that
. It is obvious that  .
.
Thus,

Taking limits as  in (2.32), we get
in (2.32), we get  .
.
Step 2.
BVP (1.4) has a positive solution in  , which is maximal positive solution.
, which is maximal positive solution.
Let

It is obvious that

Thus,  and
and  .
.
By (2.18), (2.23), and  , we have
, we have

This, together with  , yields that
, yields that

Using a proof similar to that of Step 1, we can show that

Let  be any positive solution of BVP (1.4) in
be any positive solution of BVP (1.4) in  .
.
Obviously,

This, together with  , implies
, implies

Taking limits as  in (2.39), we obtain
in (2.39), we obtain  .
.
The proof is complete.
On the other hand, we note that in these years, going with the significant developments of various differential equations in abstract spaces (cf., e.g., [3–17] and references therein), fractional differential equations in Banach spaces have also been investigated by many authors (cf. e.g., [1, 2, 18–26] and references therein). In our coming papers, we will present more results on fractional differential equations in Banach spaces.
3. An Example
Example 3.1.
Consider the following boundary value problem

where  ,
,  ,
,  ,
,  ,
,  ,
,

 ,
,  . By computation, we deduce that
. By computation, we deduce that

From Remark 2.3, we get

Therefore,

On the one hand, it is obvious that  . Thus,
. Thus,  is satisfied.
is satisfied.
For  , we see that
, we see that  , which implies that
, which implies that  holds.
holds.
Hence, by Theorem 2.5, BVP (3.1) has minimal and maximal positive solutions in  .
.
Furthermore, we can conclude that

References
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Computers & Mathematics with Applications 2010,59(3):1363-1375.
Salem HAH:On the fractional order
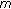 -point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009,224(2):565-572. 10.1016/j.cam.2008.05.033
-point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009,224(2):565-572. 10.1016/j.cam.2008.05.033Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Barbu V: Nonlinear Differential Equations of Monotone Types in Banach Spaces, Springer Monographs in Mathematics. Springer, New York, NY, USA; 2010:x+272.
Batty CJK, Liang J, Xiao T-J: On the spectral and growth bound of semigroups associated with hyperbolic equations. Advances in Mathematics 2005,191(1):1-10. 10.1016/j.aim.2004.01.005
Chicone C, Latushkin Y: Evolution Semigroups in Dynamical Systems and Differential Equations, Mathematical Surveys and Monographs. Volume 70. American Mathematical Society, Providence, RI, USA; 1999:x+361.
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Diagana T: Pseudo Almost Periodic Functions in Banach Spaces. Nova Science, New York, NY, USA; 2007:xiv+132.
Diagana T, Mophou GM, N'Guérékata GM: On the existence of mild solutions to some semilinear fractional integro-differential equations. Electronic Journal of Qualitative Theory of Differential Equations 2010,2010(58):1-17.
Liang J, Nagel R, Xiao T-J: Approximation theorems for the propagators of higher order abstract Cauchy problems. Transactions of the American Mathematical Society 2008,360(4):1723-1739.
Liang J, Zhang J, Xiao T-J: Composition of pseudo almost automorphic and asymptotically almost automorphic functions. Journal of Mathematical Analysis and Applications 2008,340(2):1493-1499. 10.1016/j.jmaa.2007.09.065
Lorenzi A, Mola G: Identification of unknown terms in convolution integro-differential equations in a Banach space. Journal of Inverse and Ill-Posed Problems 2010,18(3):321-355. 10.1515/JIIP.2010.013
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Second order parabolic equations in Banach spaces with dynamic boundary conditions. Transactions of the American Mathematical Society 2004,356(12):4787-4809. 10.1090/S0002-9947-04-03704-3
Xiao T-J, Liang J: Complete second order differential equations in Banach spaces with dynamic boundary conditions. Journal of Differential Equations 2004,200(1):105-136. 10.1016/j.jde.2004.01.011
Xiao T-J, Liang J: Second order differential operators with Feller-Wentzell type boundary conditions. Journal of Functional Analysis 2008,254(6):1467-1486. 10.1016/j.jfa.2007.12.012
Xiao T-J, Liang J, Zhang J: Pseudo almost automorphic solutions to semilinear differential equations in Banach spaces. Semigroup Forum 2008,76(3):518-524. 10.1007/s00233-007-9011-y
Agarwal RP, Belmekki M, Benchohra M: A survey on semilinear differential equations and inclusions involving Riemann-Liouville fractional derivative. Advances in Difference Equations 2009, 2009:-47.
Agarwal RP, Lakshmikantham V, Nieto JJ: On the concept of solution for fractional differential equations with uncertainty. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):2859-2862. 10.1016/j.na.2009.11.029
Henderson J, Ouahab A: Fractional functional differential inclusions with finite delay. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):2091-2105. 10.1016/j.na.2008.02.111
Henderson J, Ouahab A: Impulsive differential inclusions with fractional order. Computers & Mathematics with Applications 2010,59(3):1191-1226.
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Li F: Mild solutions for fractional differential equations with nonlocal conditions. Advances in Difference Equations 2010, 2010:-9.
Lv Z-W, Liang J, Xiao T-J: Solutions to fractional differential equations with nonlocal initial condition in Banach spaces. Advances in Difference Equations 2010, 2010:-10.
Mophou GM: Existence and uniqueness of mild solutions to impulsive fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1604-1615. 10.1016/j.na.2009.08.046
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lv, ZW. Positive Solutions of m-Point Boundary Value Problems for Fractional Differential Equations. Adv Differ Equ 2011, 571804 (2011). https://doi.org/10.1155/2011/571804
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/571804
 is called a cone if it satisfied the following two conditions:
is called a cone if it satisfied the following two conditions: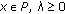 implies
implies 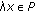 ,
,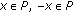 implies
implies 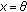 , where
, where 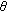 denotes the zero element of
denotes the zero element of 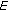 .
.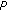 is said to be normal if there exists a constant
is said to be normal if there exists a constant 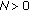 such that
such that 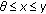 implies
implies 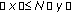 .
. -point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009,224(2):565-572. 10.1016/j.cam.2008.05.033
-point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009,224(2):565-572. 10.1016/j.cam.2008.05.033