- Research Article
- Open access
- Published:
Existence Results for a Fractional Equation with State-Dependent Delay
Advances in Difference Equations volume 2011, Article number: 642013 (2011)
Abstract
We provide sufficient conditions for the existence of mild solutions for a class of abstract fractional integrodifferential equations with state-dependent delay. A concrete application in the theory of heat conduction in materials with memory is also given.
1. Introduction
In the last two decades, the theory of fractional calculus has gained importance and popularity, due to its wide range of applications in varied fields of sciences and engineering as viscoelasticity, electrochemistry of corrosion, chemical physics, optics and signal processing, and so on. The main object of this paper is to provide sufficient conditions for the existence of mild solutions for a class of abstract partial neutral integrodifferential equations with state-dependent delay described in the form


where  ,
,  are closed linear operators defined on a common domain which is dense in a Banach space
are closed linear operators defined on a common domain which is dense in a Banach space  , and
, and  represent the Caputo derivative of
represent the Caputo derivative of  defined by
defined by

where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to  and
and  ,
,  ,
,  . The history
. The history  given by
given by  belongs to some abstract phase space
belongs to some abstract phase space  defined axiomatically, and
defined axiomatically, and  and
and  are appropriated functions.
are appropriated functions.
Functional differential equations with state-dependent delay appear frequently in applications as model of equations, and for this reason, the study of this type of equations has received great attention in the last years. The literature devoted to this subject is concerned fundamentally with first-order functional differential equations for which the state belong to some finite dimensional space, see among other works, [1–10]. The problem of the existence of solutions for partial functional differential equations with state-dependent delay has been recently treated in the literature in [11–15]. On the other hand, existence and uniqueness of solutions for fractional differential equations with delay was recently studied by Maraaba et al. in [16, 17]. In [18], the authors provide sufficient conditions for the existence of mild solutions for a class of fractional integrodifferential equations with state-dependent delay. However, the existence of mild solutions for the class of fractional integrodifferential equations with state-dependent delay of the form (1.1)-(1.2) seems to be an unread topic.
The plan of this paper is as follows. The second section provides the necessary definitions and preliminary results. In particular, we review some of the standard properties of the  -resolvent operators (see Theorem 2.11). We also employ an axiomatic definition for the phase space
-resolvent operators (see Theorem 2.11). We also employ an axiomatic definition for the phase space  which is similar to those introduced in [19]. In the third section, we use fixed-point theory to establish the existence of mild solutions for the problem (1.1). To show how easily our existence theory can be used in practice, in the fourth section, we illustrate an example.
which is similar to those introduced in [19]. In the third section, we use fixed-point theory to establish the existence of mild solutions for the problem (1.1). To show how easily our existence theory can be used in practice, in the fourth section, we illustrate an example.
2. Preliminaries
In what follows, we recall some definitions, notations, and results that we need in the sequel. Throughout this paper,  is a Banach space, and
is a Banach space, and  ,
,  , are closed linear operators defined on a common domain
, are closed linear operators defined on a common domain  which is dense in
which is dense in  ; the notations
; the notations  and
and  represent the resolvent set of the operator
represent the resolvent set of the operator  and the domain of
and the domain of  endowed with the graph norm, respectively. For
endowed with the graph norm, respectively. For  , we fix
, we fix  , and we represent by
, and we represent by  the norm of
the norm of  in
in  . Let
. Let  and
and  be Banach spaces. In this paper, the notation
be Banach spaces. In this paper, the notation  stands for the Banach space of bounded linear operators from
stands for the Banach space of bounded linear operators from  into
into  endowed with the uniform operator topology, and we abbreviate this notation to
endowed with the uniform operator topology, and we abbreviate this notation to  when
when  . Furthermore, for appropriate functions
. Furthermore, for appropriate functions  , the notation
, the notation  denotes the Laplace transform of
denotes the Laplace transform of  . The notation
. The notation  stands for the closed ball with center at
stands for the closed ball with center at  and radius
and radius  in
in  . On the other hand, for a bounded function
. On the other hand, for a bounded function  and
and  , the notation
, the notation  is given by
is given by

and we simplify this notation to  when no confusion about the space
when no confusion about the space  arises.
arises.
We will define the phase space  axiomatically, using ideas and notations developed in [19]. More precisely,
axiomatically, using ideas and notations developed in [19]. More precisely,  will denote the vector space of functions defined from
will denote the vector space of functions defined from  into
into  endowed with a seminorm denoted
endowed with a seminorm denoted  , and such that the following axioms hold.
, and such that the following axioms hold.
-
(A)
If
 ,
, 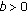 ,
, 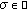 is continuous on
is continuous on  and
and  , then for every
, then for every  the following conditions hold:
the following conditions hold:-
(i)
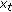 is in
is in  ,
, -
(ii)
 ,
, -
(iii)
 ,
,where
 is a constant;
is a constant; 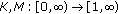 ,
, 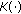 is continuous,
is continuous,  is locally bounded, and
is locally bounded, and 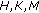 are independent of
are independent of 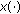 .
.
-
(i)
-
(A1)
For the function
 in (A), the function
in (A), the function  is continuous from
is continuous from  into
into 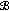 .
. -
(B)
The space
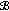 is complete.
is complete.
Example 2.1 (the phase space  ).
).
Let  , and let
, and let  be a nonnegative measurable function which satisfies the conditions (g-5), (g-6) in the terminology of [19]. Briefly, this means that
be a nonnegative measurable function which satisfies the conditions (g-5), (g-6) in the terminology of [19]. Briefly, this means that  is locally integrable and there exists a nonnegative, locally bounded function
is locally integrable and there exists a nonnegative, locally bounded function  on
on  , such that
, such that  , for all
, for all  and
and  , where
, where  is a set with Lebesgue measure zero. The space
is a set with Lebesgue measure zero. The space  consists of all classes of functions
consists of all classes of functions  , such that
, such that  is continuous on
is continuous on  , Lebesgue-measurable, and
, Lebesgue-measurable, and  is Lebesgue integrable on
is Lebesgue integrable on  . The seminorm in
. The seminorm in  is defined by
is defined by

The space  satisfies axioms (A), (A1), (B). Moreover, when
satisfies axioms (A), (A1), (B). Moreover, when  and
and  , we can take
, we can take  ,
,  , and
, and  , for
, for  (see [19, Theorem
(see [19, Theorem  ] for details).
] for details).
For additional details concerning phase space we refer the reader to [19].
To obtain our results, we assume that the integrodifferential abstract Cauchy problem


has an associated  -resolvent operator of bounded linear operators
-resolvent operator of bounded linear operators  on
on  .
.
Definition 2.2.
A one parameter family of bounded linear operators  on
on  is called a
is called a  -resolvent operator of (2.3)-(2.4) if the following conditions are verified.
-resolvent operator of (2.3)-(2.4) if the following conditions are verified.
-
(a)
The function
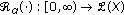 is strongly continuous and
is strongly continuous and 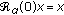 for all
for all  and
and 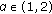 .
. -
(b)
For
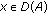 ,
, 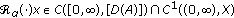 , and
, and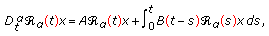 (2.5)
(2.5)

for every  .
.
The existence of a resolvent operator for problem (2.3)-(2.4) was studied in [20]. In this paper, we have considered the following conditions.
-
(P1)
The operator
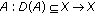 is a closed linear operator with
is a closed linear operator with 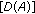 dense in
dense in 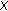 . There is positive constants
. There is positive constants 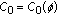 , such that
, such that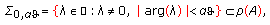 (2.7)
(2.7)where
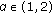 ,
, 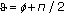 ,
, 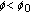 for some
for some 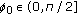 , and
, and 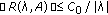 for all
for all  .
. -
(P2)
For all
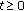 ,
, 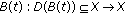 is a closed linear operator,
is a closed linear operator, 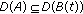 , and
, and 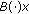 is strongly measurable on
is strongly measurable on  for each
for each  . There exists
. There exists 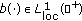 (the notation
(the notation  stands for the set of all locally integrable functions from
stands for the set of all locally integrable functions from 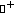 into
into 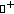 ) such that
) such that 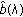 exists for
exists for 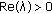 and
and 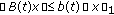 for all
for all 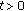 and
and 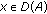 . Moreover, the operator-valued function
. Moreover, the operator-valued function  has an analytical extension (still denoted by
has an analytical extension (still denoted by 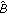 ) to
) to  such that
such that  for all
for all 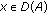 , and
, and 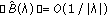 , as
, as 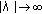 .
. -
(P3)
There exists a subspace
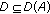 dense in
dense in 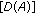 and positive constant
and positive constant 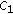 , such that
, such that 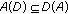 ,
,  ,
, 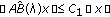 for every
for every 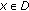 and all
and all 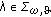 .
.
In the sequel, for  and
and  ,
,

for  ,
,  , are the paths
, are the paths

and  oriented counterclockwise. In addition,
oriented counterclockwise. In addition,  are the sets
are the sets

We now define the operator family  by
by

The following result has been established in [20, Theorem 2.1].
Theorem 2.3.
Assume that conditions (P1)–(P3) are fulfilled, then there is a unique  -resolvent operator for problem (2.3)-(2.4).
-resolvent operator for problem (2.3)-(2.4).
In what follows, we always assume that the conditions (P1)–(P3) are verified.
We consider now the nonhomogeneous problem.
In the rest of this section, we discuss existence and regularity of solutions of


where  and
and  . In the sequel,
. In the sequel,  is the operator function defined by (2.11). We begin by introducing the following concept of classical solution.
is the operator function defined by (2.11). We begin by introducing the following concept of classical solution.
Definition 2.4.
A function  ,
,  is called a classical solution of (2.12)-(2.13) on
is called a classical solution of (2.12)-(2.13) on  if
if  ; the condition (2.13) holds and (2.12) is verified on
; the condition (2.13) holds and (2.12) is verified on  .
.
Definition 2.5.
Let  , we define the family
, we define the family  by
by

for each  .
.
The proof of the next result is in [20]. For reader's convenience, we will give the proof.
Lemma 2.6.
If the function  is exponentially bounded in
is exponentially bounded in  , then
, then  is exponentially bounded in
is exponentially bounded in  .
.
Proof.
If there are constants,  such that
such that  , we obtain
, we obtain

where  .
.
The next result follows from Lemma 2.6. We will omit the proof.
Lemma 2.7.
If the function  is exponentially bounded in
is exponentially bounded in  , then
, then  is exponentially bounded in
is exponentially bounded in  .
.
We now establish a variation of constants formula for the solutions of (2.12)-(2.13). The proof of the next result is in [20]. For reader's convenience, we will give the proof.
Theorem 2.8.
Let  . Assume that
. Assume that  and
and  is a classical solution of (2.12)-(2.13) on
is a classical solution of (2.12)-(2.13) on  , then
, then

Proof.
The Cauchy problem (2.12)-(2.13) is equivalent to the Volterra equation

and the  -resolvent equation (2.6) is equivalent to
-resolvent equation (2.6) is equivalent to

To prove (2.16), we notice that

Therefore,

We obtain

It is clear from the preceding definition that  is a solution of problem (2.3)-(2.4) on
is a solution of problem (2.3)-(2.4) on  for
for  .
.
Definition 2.9.
Let  . A function
. A function  is called a mild solution of (2.12)-(2.13) if
is called a mild solution of (2.12)-(2.13) if

The proof of the next result is in [20]. For reader's convenience, we will give the proof.
Theorem 2.10.
Let  and
and  . If
. If  , then the mild solution of (2.12)-(2.13) is a classical solution.
, then the mild solution of (2.12)-(2.13) is a classical solution.
Proof.
To begin with, we study the case in which  . Let
. Let  be the mild solution of (2.12)-(2.13) and assume that
be the mild solution of (2.12)-(2.13) and assume that  . It is easy to see that
. It is easy to see that  and
and

where  is given by
is given by  . From [7, Lemma 3.12], we obtain that
. From [7, Lemma 3.12], we obtain that  is a classical solution and satisfies
is a classical solution and satisfies

Moreover, from (2.24) and taking into account that  for all
for all  and
and  , we deduce the existence of constants
, we deduce the existence of constants  ,
,  (which are independent from
(which are independent from  ) such that
) such that

Now, we assume that  . Let
. Let  be a sequence in
be a sequence in  such that
such that  in
in  . From [7, Lemma 3.12], we know that
. From [7, Lemma 3.12], we know that  ,
,  , is a classical solution of (2.12)-(2.13) with
, is a classical solution of (2.12)-(2.13) with  in the place of
in the place of  . By using the estimate (2.25), we deduce the existence of functions
. By using the estimate (2.25), we deduce the existence of functions  , such that
, such that  in
in  and
and  in
in  . These facts, jointly with our assumptions on
. These facts, jointly with our assumptions on  , permit to conclude that
, permit to conclude that  in
in  . On the other hand,
. On the other hand,

we obtain

Now, by making  on
on

we conclude that  is a classical solution of (2.12)-(2.13). The proof is finished.
is a classical solution of (2.12)-(2.13). The proof is finished.
The proof of the next result is in [20]. For reader's convenience, we will give the proof.
Theorem 2.11.
Let  and
and  . If
. If  , then the mild solution of (2.12)-(2.13) is a classical solution.
, then the mild solution of (2.12)-(2.13) is a classical solution.
Proof.
Let  , there is
, there is  on
on  such that
such that  on
on  and
and  on
on  . Put
. Put  proceeding as in the proof of Theorem 2.10. It follows that
proceeding as in the proof of Theorem 2.10. It follows that  is a classical solution of (2.12)-(2.13). Moreover, from [7, Lemma 3.13], we obtain
is a classical solution of (2.12)-(2.13). Moreover, from [7, Lemma 3.13], we obtain

from which we deduce the existence of positive constants  (independent from
(independent from  ) such that
) such that

With similar arguments as in the proof of Theorem 2.10, we conclude that  is a classical solution of (2.12)-(2.13). We omit additional details. The proof is completed.
is a classical solution of (2.12)-(2.13). We omit additional details. The proof is completed.
To establish our existence results, we need the following Lemma.
Lemma 2.12.
Let  . If
. If  is compact for some
is compact for some  , then
, then  and
and  are compact for all
are compact for all  .
.
Proof.
From the resolvent identity, it follows that  is compact for every
is compact for every  . We have from [20, Lemma 2.2] that
. We have from [20, Lemma 2.2] that  is a compact operator for
is a compact operator for  ; therefore,
; therefore,  is a compact operator for
is a compact operator for  .
.
From [20, Lemma 2.5], we have,  is uniformly continuous for
is uniformly continuous for  , for any
, for any  fixed, we can select points
fixed, we can select points  , such that if
, such that if  , we obtain
, we obtain  , for all
, for all  and
and  .
.
Therefore, for all  , we have that
, we have that

Noting now that

from (2.31), we find that

Thus,

where  is compact and
is compact and  , then we observe that
, then we observe that  as
as  . This permits us to conclude that
. This permits us to conclude that  is relatively compact in
is relatively compact in  . This proves that
. This proves that  is a compact operator for all
is a compact operator for all  .
.
For completeness, we include the following well-known result.
Theorem 2.13 (Leray-Schauder alternative, [21, Theorem  ]).
]).
Let  be a closed convex subset of a Banach space
be a closed convex subset of a Banach space  with
with  . Let
. Let  be a completely continuous map. Then,
be a completely continuous map. Then,  has a fixed point in
has a fixed point in  or the set
or the set  is unbounded.
is unbounded.
3. Existence Results
In this section, we study the existence of mild solutions for system (1.1)-(1.2). Along this section,  is a positive constant such that
is a positive constant such that  and
and  for every
for every  . We adopt the notion of mild solutions for (1.1)-(1.2) from the one given in [20].
. We adopt the notion of mild solutions for (1.1)-(1.2) from the one given in [20].
Definition 3.1.
A function  is called a mild solution of the neutral system (1.1)-(1.2) on
is called a mild solution of the neutral system (1.1)-(1.2) on  if
if  ,
,  , and
, and

To prove our results, we always assume that  is continuous and that
is continuous and that  . If
. If  , we define
, we define  as the extension of
as the extension of  to
to  such that
such that  . We define
. We define  such that
such that  where
where  is the extension of
is the extension of  , such that
, such that  for
for  .
.
In the sequel, we introduce the following conditions.
-
(H1)
The function
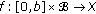 verifies the following conditions:
verifies the following conditions:-
(i)
the function
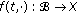 is continuous for every
is continuous for every 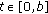 , and for every
, and for every  , the function
, the function 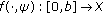 is strongly measurable,
is strongly measurable, -
(ii)
there exist
 and a continuous nondecreasing function
and a continuous nondecreasing function 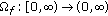 , such that
, such that 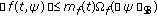 , for all
, for all 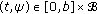 .
.
-
(i)
-
(H2)
For all
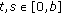 ,
, 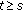 and
and 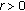 , the set
, the set  is bounded in
is bounded in  .
. -
(Hφ)
The function
 is well defined and continuous from the set
is well defined and continuous from the set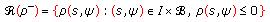 (3.2)
(3.2)into
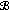 , and there exists a continuous and bounded function
, and there exists a continuous and bounded function  , such that
, such that  for every
for every  .
.
Remark 3.2.
The condition  is frequently verified by continuous and bounded functions.
is frequently verified by continuous and bounded functions.
Remark 3.3.
In the rest of this section,  and
and  are the constants
are the constants  and
and  .
.
Lemma 3.4 (see [13, Lemma 2.1]).
Let  be continuous on
be continuous on  and
and  . If
. If  holds, then
holds, then

 , where
, where  .
.
Theorem 3.5.
Let conditions  ,
,  , and
, and  hold, and assume that
hold, and assume that  . If
. If  , then there exists a mild solution of (1.1)-(1.2) on
, then there exists a mild solution of (1.1)-(1.2) on  .
.
Proof.
Let  be the extension of
be the extension of  to
to  such that
such that  on
on  . Consider the space
. Consider the space  endowed with the uniform convergence topology and define the operator
endowed with the uniform convergence topology and define the operator  by
by

for  . It is easy to see that
. It is easy to see that  . We prove that there exists
. We prove that there exists  such that
such that  . If this property is false, then for every
. If this property is false, then for every  there exist
there exist  and
and  such that
such that  . Then, from Lemma 3.4, we find that
. Then, from Lemma 3.4, we find that

and hence,

which contradicts our assumption.
Let  be such that
be such that  , in the sequel;
, in the sequel;  and
and  are the numbers defined by
are the numbers defined by  and
and  . To prove that
. To prove that  is a condensing operator, we introduce the decomposition
is a condensing operator, we introduce the decomposition  , where
, where

for  .
.
It is easy to see that  is continuous and a contraction on
is continuous and a contraction on  . Next, we prove that
. Next, we prove that  is completely continuous from
is completely continuous from  into
into  .
.
Step 1.
Let  , and let
, and let  be a positive real number such that
be a positive real number such that  . We can infer that
. We can infer that

where  ,
,  is the convex hull of the set
is the convex hull of the set  and
and  , since
, since

which proves that  is relatively compact in
is relatively compact in  .
.
Step 2.
The set  is equicontinuous on
is equicontinuous on  .
.
Let  and
and  such that
such that  for every
for every  with
with  . Under these conditions, for
. Under these conditions, for  and
and  with
with  , we get
, we get

which shows that the set of functions  is right equicontinuity at
is right equicontinuity at  . A similar procedure permits us to prove the right equicontinuity at zero and the left equicontinuity at
. A similar procedure permits us to prove the right equicontinuity at zero and the left equicontinuity at  . Thus,
. Thus,  is equicontinuous. By using a similar procedure to proof of the [13, Theorem 2.3], we prove that that
is equicontinuous. By using a similar procedure to proof of the [13, Theorem 2.3], we prove that that  is continuous on
is continuous on  , which completes the proof
, which completes the proof  is completely continuous.
is completely continuous.
The existence of a mild solution for (1.1)-(1.2) is now a consequence of [22, Theorem  ]. This completes the proof.
]. This completes the proof.
Theorem 3.6.
Let conditions  ,
,  ,
,  hold,
hold,  for every
for every  , and assume that
, and assume that  . If
. If

where  , then there exists a mild solution of (1.1)-(1.2) on
, then there exists a mild solution of (1.1)-(1.2) on  .
.
Proof.
Let  be the operator defined by (3.4). In the sequel we use Theorem 2.13. If
be the operator defined by (3.4). In the sequel we use Theorem 2.13. If  ,
,  , then from Lemma 3.4, we have that
, then from Lemma 3.4, we have that

since  for every
for every  . If
. If  , we obtain that
, we obtain that

Denoting by  the right-hand side of the last inequality, we obtain that
the right-hand side of the last inequality, we obtain that

and hence

This inequality and (3.11) permit us to conclude that the set of functions  is bounded, which in turn shows that
is bounded, which in turn shows that  is bounded.
is bounded.
By using a similar procedure allows to proof Theorem 3.5, we obtain that  is completely continuous. By Theorem 2.13, the proof is ended.
is completely continuous. By Theorem 2.13, the proof is ended.
4. Example
To finish this section, we apply our results to study an integrodifferential equation which arises in the theory of heat equation. Consider the system

In this system,  ,
,  ,
,  are positive numbers and
are positive numbers and  . To represent this system in the abstract form (1.1)-(1.2), we choose the spaces
. To represent this system in the abstract form (1.1)-(1.2), we choose the spaces  and
and  , see Example 2.1 for details. In the sequel,
, see Example 2.1 for details. In the sequel,  is the operator given by
is the operator given by  with domain
with domain  . It is well known that
. It is well known that  is the infinitesimal generator of an analytic semigroup
is the infinitesimal generator of an analytic semigroup  on
on  . Hence,
. Hence,  is sectorial of type and (P1) is satisfied. We also consider the operator
is sectorial of type and (P1) is satisfied. We also consider the operator  ,
,  ,
,  for
for  . Moreover, it is easy to see that conditions (P2)-(P3) in Section 2 are satisfied with
. Moreover, it is easy to see that conditions (P2)-(P3) in Section 2 are satisfied with  and
and  , where
, where  is the space of infinitely differentiable functions that vanish at
is the space of infinitely differentiable functions that vanish at  and
and  .
.
We next consider the problem of the existence of mild solutions for the system (4.1). To this end, we introduce the following functions:

Under the above conditions, we can represent the system (4.1) in the abstract form (2.12)-(2.13). The following result is a direct consequence of Theorem 3.5.
Proposition 4.1.
Let  be such that condition
be such that condition  holds, the functions
holds, the functions  are bounded, and assume that the above conditions are fulfilled, then there exists a mild solution of (4.1) on
are bounded, and assume that the above conditions are fulfilled, then there exists a mild solution of (4.1) on  .
.
References
Bartha M: Periodic solutions for differential equations with state-dependent delay and positive feedback. Nonlinear Analysis: Theory, Methods & Applications 2003,53(6):839-857. 10.1016/S0362-546X(03)00039-7
Cao Y, Fan J, Gard TC: The effects of state-dependent time delay on a stage-structured population growth model. Nonlinear Analysis: Theory, Methods & Applications 1992,19(2):95-105. 10.1016/0362-546X(92)90113-S
Domoshnitsky A, Drakhlin M, Litsyn E: On equations with delay depending on solution. Nonlinear Analysis: Theory, Methods & Applications 2002,49(5):689-701. 10.1016/S0362-546X(01)00132-8
Chen F, Sun D, Shi J: Periodicity in a food-limited population model with toxicants and state dependent delays. Journal of Mathematical Analysis and Applications 2003,288(1):136-146. 10.1016/S0022-247X(03)00586-9
Hartung F: Linearized stability in periodic functional differential equations with state-dependent delays. Journal of Computational and Applied Mathematics 2005,174(2):201-211. 10.1016/j.cam.2004.04.006
Hartung F: Parameter estimation by quasilinearization in functional differential equations with state-dependent delays: a numerical study. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4557-4566. 10.1016/S0362-546X(01)00569-7
Hartung F, Herdman TL, Turi J: Parameter identification in classes of neutral differential equations with state-dependent delays. Nonlinear Analysis: Theory, Methods & Applications 2000,39(3):305-325. 10.1016/S0362-546X(98)00169-2
Kuang Y, Smith HL: Slowly oscillating periodic solutions of autonomous state-dependent delay equations. Nonlinear Analysis: Theory, Methods & Applications 1992,19(9):855-872. 10.1016/0362-546X(92)90055-J
Torrejón R: Positive almost periodic solutions of a state-dependent delay nonlinear integral equation. Nonlinear Analysis: Theory, Methods & Applications 1993,20(12):1383-1416. 10.1016/0362-546X(93)90167-Q
Li Y: Periodic solutions for delay Lotka-Volterra competition systems. Journal of Mathematical Analysis and Applications 2000,246(1):230-244. 10.1006/jmaa.2000.6784
dos Santos JPC: On state-dependent delay partial neutral functional integro-differential equations. Applied Mathematics and Computation 2010,216(5):1637-1644. 10.1016/j.amc.2010.03.019
dos Santos JPC: Existence results for a partial neutral integro-differential equation with state-dependent delay. Electronic Journal of Qualitative Theory of Differential Equations 2010,2010(29):1-12.
Hernández E, Prokopczyk A, Ladeira L: A note on partial functional differential equations with state-dependent delay. Nonlinear Analysis: Real World Applications 2006,7(4):510-519. 10.1016/j.nonrwa.2005.03.014
Hernández M E, McKibben MA: On state-dependent delay partial neutral functional-differential equations. Applied Mathematics and Computation 2007,186(1):294-301. 10.1016/j.amc.2006.07.103
Hernández Morales E, McKibben MA, Henríquez HR: Existence results for partial neutral functional differential equations with state-dependent delay. Mathematical and Computer Modelling 2009,49(5-6):1260-1267. 10.1016/j.mcm.2008.07.011
Maraaba T, Baleanu D, Jarad F: Existence and uniqueness theorem for a class of delay differential equations with left and right Caputo fractional derivatives. Journal of Mathematical Physics 2008,49(8):-11.
Maraaba T, Jarad F, Baleanu D: On the existence and the uniqueness theorem for fractional differential equations with bounded delay within Caputo derivatives. Science in China Series A 2008,51(10):1775-1786. 10.1007/s11425-008-0068-1
Agarwal R, de Andrade B, Siracusa G: On fractional integro-differential equations with state-dependent delay. to appear in Computers & Mathematics with Applications
Hino Y, Murakami S, Naito T: Functional-Differential Equations with Infinite Delay, Lecture Notes in Mathematics. Volume 1473. Springer, Berlin, Germany; 1991:x+317.
Agarwal R, dos Santos JPC, Cuevas C: Analytic resolvent operator and existence results for fractional integro-differential equations. submitted
Granas A, Dugundji J: Fixed Point Theory, Springer Monographs in Mathematics. Springer, New York, NY, USA; 2003:xvi+690.
Martin RH Jr.: Nonlinear Operators and Differential Equations in Banach Spaces. Robert E. Krieger Publishing, Melbourne, Fla, USA; 1987:xiv+440.
Acknowledgments
The final version of this paper was finished while the third author was visiting the Universidade Federal de Pernambuco (Recife, Brasil) during Desember 2010-January 2011. The third author would like to thank the Functional Equations Group for their kind invitation and hospitality. The authors are grateful to the referees for pointing out omissions and misprints, and demanding vigorously details and clarifications. J. P. C. dos Santos is partially supported by FAPEMIG/Brazil under Grant no. CEX-APQ-00476-09. C. Cuevas is partially supported by CNPQ/Brazil under Grant no. 300365/2008-0. B. de Andrade is partially supported by CNPQ/Brazil under Grant no. 100994/2011-3.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
dos Santos, J.P.C., Cuevas, C. & de Andrade, B. Existence Results for a Fractional Equation with State-Dependent Delay. Adv Differ Equ 2011, 642013 (2011). https://doi.org/10.1155/2011/642013
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/642013
 ,
, 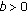 ,
, 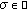 is continuous on
is continuous on  and
and  , then for every
, then for every  the following conditions hold:
the following conditions hold: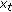 is in
is in  ,
, ,
, ,
, is a constant;
is a constant; 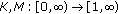 ,
, 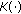 is continuous,
is continuous,  is locally bounded, and
is locally bounded, and 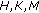 are independent of
are independent of 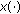 .
. in (A), the function
in (A), the function  is continuous from
is continuous from  into
into 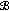 .
.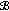 is complete.
is complete.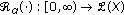 is strongly continuous and
is strongly continuous and 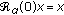 for all
for all  and
and 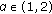 .
.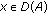 ,
, 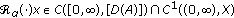 , and
, and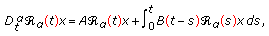
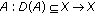 is a closed linear operator with
is a closed linear operator with 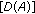 dense in
dense in 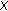 . There is positive constants
. There is positive constants 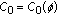 , such that
, such that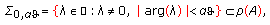
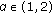 ,
, 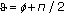 ,
, 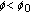 for some
for some 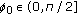 , and
, and 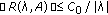 for all
for all  .
.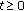 ,
, 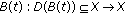 is a closed linear operator,
is a closed linear operator, 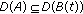 , and
, and 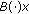 is strongly measurable on
is strongly measurable on  for each
for each  . There exists
. There exists 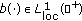 (the notation
(the notation  stands for the set of all locally integrable functions from
stands for the set of all locally integrable functions from 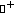 into
into 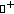 ) such that
) such that 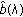 exists for
exists for 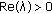 and
and 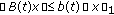 for all
for all 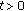 and
and 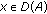 . Moreover, the operator-valued function
. Moreover, the operator-valued function  has an analytical extension (still denoted by
has an analytical extension (still denoted by 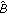 ) to
) to  such that
such that  for all
for all 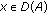 , and
, and 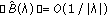 , as
, as 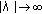 .
.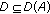 dense in
dense in 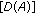 and positive constant
and positive constant 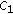 , such that
, such that 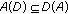 ,
,  ,
, 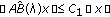 for every
for every 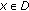 and all
and all 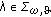 .
.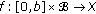 verifies the following conditions:
verifies the following conditions: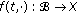 is continuous for every
is continuous for every 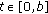 , and for every
, and for every  , the function
, the function 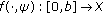 is strongly measurable,
is strongly measurable, and a continuous nondecreasing function
and a continuous nondecreasing function 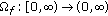 , such that
, such that 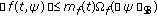 , for all
, for all 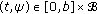 .
.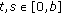 ,
, 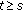 and
and 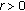 , the set
, the set  is bounded in
is bounded in  .
. is well defined and continuous from the set
is well defined and continuous from the set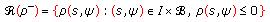
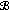 , and there exists a continuous and bounded function
, and there exists a continuous and bounded function  , such that
, such that  for every
for every  .
.