- Research Article
- Open access
- Published:
An Effective Numerical Method and Its Utilization to Solution of Fractional Models Used in Bioengineering Applications
Advances in Difference Equations volume 2011, Article number: 652789 (2011)
Abstract
This paper deals with the fractional-order linear and nonlinear models used in bioengineering applications and an effective method for their numerical solution. The proposed method is based on the power series expansion of a generating function. Numerical solution is in the form of the difference equation, which can be simply applied in the Matlab/Simulink to simulate the dynamics of system. Several illustrative examples are presented, which can be widely used in bioengineering as well as in the other disciplines, where the fractional calculus is often used.
1. Introduction
Recently, fractional calculus has played an increasing role in modeling complex phenomena in the fields of physics, chemistry, biology, and engineering (e.g., [1–4]). The main characteristic of fractional derivatives, or more precisely derivatives of positive real order, is so called the "memory effect". It is well known that the state of many systems (biological, electrochemical, viscoelastic, etc.) at a given time depends on their configuration at previous times. The fractional derivative takes into account this history in its definition as a convolution with a function whose amplitude decays at earlier times as a power-law. Thus, the fractional derivative is natural to use when modeling biological systems in various bioengineering applications.
In this paper, we offer applications of fractional calculus in bioengineering, which are described by the fractional differential equations. Paper is organized as follows: basic definitions of fractional calculus, fractional-order systems and numerical method are presented first in Section 2. Three representative fractional-order models often used in bioengineering are described and numerically solved in Section 3. In Section 4 the questions of numerical analysis are discussed. Some conclusion remarks are mentioned in Section 5.
2. Preliminaries
2.1. Fractional Calculus
Fractional calculus is a topic in mathematics that is more than 300 years old. The idea of fractional calculus was suggested early in the development of regular (integer-order) calculus, with the first literature reference being associated with a letter, from Leibniz to L'Hospital in 1695. In this letter the half-order derivative was first mentioned.
There are several definitions of the fractional derivative/integral as a one common operator known as "differintegral" (see, e.g., [4–6]):
The Riemann-Liouville (RL) definition is given as

for  and where
and where  is the Gamma function.
is the Gamma function.
The Caputo's definition of fractional derivatives can be written as

for  .
.
If we consider  , where
, where  is a real constant and
is a real constant and  means the integer part, we can write the Grünwald-Letnikov (GL) definition as
means the integer part, we can write the Grünwald-Letnikov (GL) definition as

where  and
and  are the bounds of operation for
are the bounds of operation for  . Usually, we assume lower boundary
. Usually, we assume lower boundary  .
.
For many engineering applications the Laplace transform methods are often used. The Laplace transform of the RL, the GL, and Caputo's fractional derivative/integral, under zero initial conditions for order  is given by [5]:
is given by [5]:

A function, which plays a very important role in the fractional calculus, was in fact introduced by Humbert and Agarwal [7]. It is a two-parameter function of the Mittag-Leffler type defined as [4]:

Note that fractional calculus holds many important and interesting properties, which were described for instance in [3–5].
2.2. Fractional-Order Systems
There are several possible interpretations of the fractional-order systems. Here are mentioned three of them.
A general fractional-order linear system can be described by a fractional differential equation of the form [4]:

where  denotes the Riemann-Liouville, Caputo's or Grünwald-Letnikov fractional derivative depending on initial conditions and their physical meaning or by the corresponding transfer function of incommensurate real orders of the following form [4]:
denotes the Riemann-Liouville, Caputo's or Grünwald-Letnikov fractional derivative depending on initial conditions and their physical meaning or by the corresponding transfer function of incommensurate real orders of the following form [4]:

where  ,
,  are constants, and
are constants, and  ,
,  are arbitrary real or rational numbers and without loss of generality they can be arranged as
are arbitrary real or rational numbers and without loss of generality they can be arranged as  , and
, and  .
.
The fractional-order linear time-invariant system can also be represented by the following state-space model:

where  ,
,  , and
, and  are the state, input and output vectors of the system and
are the state, input and output vectors of the system and  ,
,  ,
,  , and
, and  are the fractional orders. If
are the fractional orders. If  , system (2.8) is called a commensurate-order system, otherwise it is an incommensurate-order system.
, system (2.8) is called a commensurate-order system, otherwise it is an incommensurate-order system.
In this paper, we will also consider the general incommensurate fractional-order nonlinear system represented as follows:

where  are nonlinear functions and
are nonlinear functions and  are initial conditions. The vector representation of (2.9) is:
are initial conditions. The vector representation of (2.9) is:

where  for
for  ,
,  and
and  .
.
The equilibrium points of system (2.10) are calculated via solving the following equation

and we suppose that  is an equilibrium point of the fractional-order nonlinear system (2.10).
is an equilibrium point of the fractional-order nonlinear system (2.10).
2.3. Discrete Time Approximation of Fractional Calculus: Numerical Method
In general, if a function  is approximated by a grid function,
is approximated by a grid function,  , where
, where  is the grid size, the approximation for its fractional derivative of order
is the grid size, the approximation for its fractional derivative of order  can be expressed as [8]:
can be expressed as [8]:

where  is the backward shift operator and
is the backward shift operator and  is a generating function. This generating function and its expansion determine both the form of the approximation and the coefficients [9]. In this way, the discretization of continuous fractional-order differentiator/integrator
is a generating function. This generating function and its expansion determine both the form of the approximation and the coefficients [9]. In this way, the discretization of continuous fractional-order differentiator/integrator 
 can be expressed as
can be expressed as  . It is known that the forward difference rule is not suitable for applications to causal problems [8, 9].
. It is known that the forward difference rule is not suitable for applications to causal problems [8, 9].
As a generating function,  can be used in generally the following formula [10]:
can be used in generally the following formula [10]:

where  and
and  are denoted the gain and phase tuning parameters, respectively, and
are denoted the gain and phase tuning parameters, respectively, and  is sampling period. For example, when
is sampling period. For example, when  and
and  , the generating function (2.13) becomes the forward Euler, the Tustin, the Al-Alaoui, the backward Euler, the implicit Adams rules, respectively. In this sense the generating formula can be tuned more precisely.
, the generating function (2.13) becomes the forward Euler, the Tustin, the Al-Alaoui, the backward Euler, the implicit Adams rules, respectively. In this sense the generating formula can be tuned more precisely.
The expansion of the generating functions can be done by power series expansion (PSE). It is very important to note that PSE scheme leads to approximations in the form of polynomials of degree  , that is, the discretized fractional order derivative is in the form of finite impulse response (FIR) filters, which have only zeros [11].
, that is, the discretized fractional order derivative is in the form of finite impulse response (FIR) filters, which have only zeros [11].
In this paper, for directly discretizing  ,
,  , we will concentrate on the FIR form of discretization where as a generating function we will adopt a backward Euler rule. The mentioned operator, obtained from (2.13) for
, we will concentrate on the FIR form of discretization where as a generating function we will adopt a backward Euler rule. The mentioned operator, obtained from (2.13) for  , raised to power
, raised to power  , has the form
, has the form

Then, the resulting transfer function, approximating the fractional-order operators, can be obtained by applying the relationship [12]:

where  is the
is the  transform of the output sequence
transform of the output sequence  ,
,  is the
is the  transform of the input sequence
transform of the input sequence  , and
, and denotes the expression, which results from the power series expansion of the function
denotes the expression, which results from the power series expansion of the function  .
.
Doing so gives [13]:

where  denotes the discrete equivalent of the fractional-order operator, considered as processes, and
denotes the discrete equivalent of the fractional-order operator, considered as processes, and  is the polynomial with degree
is the polynomial with degree  of variable
of variable  .
.
By using the short memory principle [4], the discrete equivalent of the fractional-order integrodifferential operator,  , is given by
, is given by

where  is the memory length and
is the memory length and  are binomial coefficients
are binomial coefficients  where [14]
where [14]

For practical numerical calculation of the fractional derivative and integral we can derive the formula from relation (2.17), where the sampling period  is in numerical evaluation replaced by the time step of calculation
is in numerical evaluation replaced by the time step of calculation  , then we get
, then we get

where  for
for  or
or  for
for  in the relation (2.19). By using a relation (2.14) we obtained a first-order approximation
in the relation (2.19). By using a relation (2.14) we obtained a first-order approximation  of the fractional derivative of order
of the fractional derivative of order  . Another possibility for the approximation is use, the trapezoidal rule, that is, the use of the generating function (2.13) for
. Another possibility for the approximation is use, the trapezoidal rule, that is, the use of the generating function (2.13) for  and then the PSE, which is convergent of order 2. Other forms of generation functions for higher-order approximation of the fractional order derivative
and then the PSE, which is convergent of order 2. Other forms of generation functions for higher-order approximation of the fractional order derivative  are presented in [9].
are presented in [9].
Obviously, for this simplification we pay a penalty in the form of some inaccuracy. If  , we can easily establish the following estimate for determining the memory length
, we can easily establish the following estimate for determining the memory length  , providing the required accuracy
, providing the required accuracy  [4]:
[4]:

An evaluation of the short memory effect and convergence relation of the error between short and long memory were clearly described and also proved in [4].
For general numerical solution of the fractional differential equation, let us consider the following initial value problem

with initial conditions  , where
, where  . Using approximation (2.19), we obtain the numerical solution, which can be expressed as
. Using approximation (2.19), we obtain the numerical solution, which can be expressed as

where  . For the memory term expressed by sum, a "short memory" principle can be used or without using "short memory" principle, we put
. For the memory term expressed by sum, a "short memory" principle can be used or without using "short memory" principle, we put  for all
for all  in (2.22).
in (2.22).
3. Fractional-Order Models in Bioengineering Applications
There are many fractional-order models, which were already used in bioengineering applications as for example [3, 4, 15]: model of neuron, bioelectrode model, model of respiratory mechanics, compartmental model of pharmacokinetics, and so forth, In this section we mention and describe only three of them, namely model of the cells, nuclear magnetic resonance (NMR) model, and Lotka-Volterra (parasite-host or predator-prey) model.
3.1. Fractional-Order Viscoelastic Models of Cells
Cells have an essential biological roles and often change shape, attach and detach from surface, and sometimes divide. Such activities require the deformation in response to local stress. The rheological behavior of these cells can be modeled with the following fractional differential equation [3]:

where  is stress,
is stress,  is strain,
is strain,  is the static elastic modulus,
is the static elastic modulus,  is fractional relaxation time constant, and
is fractional relaxation time constant, and  is the viscosity.
is the viscosity.
If we apply the Laplace transform to system (3.1), assuming that the initial conditions are all zeros, we obtain

As it was mentioned in [3], the parameter  can be neglected. For a step function
can be neglected. For a step function  in applied stress,
in applied stress,  , the creep response can be written as
, the creep response can be written as

The inverse Laplace transform of this expression can be written by using a Laplace transform of the Mittag-Leffler function [4]:

and we obtain an analytical solution in the form

For numerical solution of the fractional differential equation (3.1) for  , we can use relations (2.18) and (2.19). The resulting difference equation has the form
, we can use relations (2.18) and (2.19). The resulting difference equation has the form

where  for
for  , where
, where  and
and  is time step of calculation, and
is time step of calculation, and  is obtained from initial condition, for example,
is obtained from initial condition, for example,  for zero initial condition.
for zero initial condition.
Let us assume the following model parameters:  , zero initial condition,
, zero initial condition,  sec,
sec,  , and
, and  .
.
Comparison of the analytical solution (3.5) and the numerical solution (3.6) of the fractional differential equation (3.1) for the parameters  ,
,  , zero initial condition,
, zero initial condition,  sec,
sec,  , and
, and  is depicted in Figure 1.
is depicted in Figure 1.
As we can observe in Figure 1, the numerical solution fits the analytical solution and we can say that both solutions are consistent.
3.2. Fractional-Order Bloch Equations in NMR
In physics and bioengineering, specifically in NMR or magnetic resonance imaging, the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization  as a function of time when relaxation times are
as a function of time when relaxation times are  (spin-lattice) and
(spin-lattice) and  (spin-spin). The physical basis for
(spin-spin). The physical basis for  relaxation involves the protons losing their energy to the surrounding lattice, hence the name spin-lattice relaxation.
relaxation involves the protons losing their energy to the surrounding lattice, hence the name spin-lattice relaxation.  involves the loss of phase coherence between the protons processing in the transverse plane. Different tissues in the body have different values of
involves the loss of phase coherence between the protons processing in the transverse plane. Different tissues in the body have different values of  and
and  . The values depend on the strength of the magnetic field.
. The values depend on the strength of the magnetic field.
Now, we consider the fractional-order Bloch equations, where integer-order derivatives are replaced by fractional-order ones. Mathematical description of the fractional-order system with Caputo's derivatives is expressed as [16]

where  ,
,  , and
, and  are the derivative orders. Here,
are the derivative orders. Here,  ,
,  , and
, and  have the units of
have the units of  to maintain a consistent set of units for the magnetization.
to maintain a consistent set of units for the magnetization.
Numerical solution of Bloch equations (3.7) was obtained by using the relationship (2.22), which leads to solution in the form [17]:

where  is the simulation time,
is the simulation time,  , for
, for  , and (
, and ( ,
,  ,
,  ) is the start point (initial conditions).
) is the start point (initial conditions).
Comparison of the proposed numerical solution (3.8) with an analytical solution has been done in [17] and obtained results show a good consistency of both solutions. In aforementioned work the Matlab function and the Matlab/Simulink model for solution of the fractional-order Bloch equations (3.7) have also been created, which can be widely used for simulations with various parameters  ,
,  ,
,  , and
, and  for desired simulation time
for desired simulation time  and initial conditions (
and initial conditions ( ,
,  ,
,  ).
).
Let us consider the following parameters for tissue—gray matter of brain—for a magnetic field strength of 1.5 T from [18]:  ,
,  ,
,  , equilibrium
, equilibrium  , orders
, orders  , and
, and  , respectively.
, respectively.
Numerical solution (state space trajectory) of the fractional-order Bloch equations (3.7) with parameters:  ,
,  ,
,  ,
,  ,
,  , and initial conditions
, and initial conditions  ,
,  ,
,  obtained by equations (3.8) for
obtained by equations (3.8) for  ,
,  , and
, and  is depicted in Figure 2. State space trajectory for the integer-order Bloch equations with the same parameters is depicted in Figure 3.
is depicted in Figure 2. State space trajectory for the integer-order Bloch equations with the same parameters is depicted in Figure 3.
We can observe in both figures that fractional orders in the Bloch equations provide expanded model with different behavior for describing a more general NMR, which can find applications in complex materials exhibiting memory.
3.3. Fractional-Order Lotka-Volterra System
The fractional-order Lotka-Volterra (or fractional-order predator-prey model or parasite-host) system was proposed and described as [19]:

where  are prey and predator densities, respectively, and all constants
are prey and predator densities, respectively, and all constants  ,
,  ,
,  ,
,  ,
,  are positive. For
are positive. For  and
and  we obtain a well-known model proposed by Alfred Lotka in 1910 and independently by Vito Volterra in 1926.
we obtain a well-known model proposed by Alfred Lotka in 1910 and independently by Vito Volterra in 1926.
The stability analysis and numerical solutions of such kind of system have been already studied in [19]. There are two equilibria, when the system (3.9) is solved for  and
and  . The above system of equations yields to
. The above system of equations yields to  and
and  if
if  . The stability of the equilibrium point
. The stability of the equilibrium point  is of importance. If it were stable, nonzero populations might be attracted towards it. However, as the fixed point at the origin is a saddle point, and hence unstable, we find that the extinction of both species is difficult in the model. The second fixed point
is of importance. If it were stable, nonzero populations might be attracted towards it. However, as the fixed point at the origin is a saddle point, and hence unstable, we find that the extinction of both species is difficult in the model. The second fixed point  is not hyperbolic, so no conclusions can be drawn from the linear analysis. However, the system admits a constant of motion and the level curves are closed trajectories surrounding the fixed point. Consequently, the levels of the predator and prey populations cycle and oscillate around this fixed point.
is not hyperbolic, so no conclusions can be drawn from the linear analysis. However, the system admits a constant of motion and the level curves are closed trajectories surrounding the fixed point. Consequently, the levels of the predator and prey populations cycle and oscillate around this fixed point.
Numerical solution of the fractional-order Lotka-Volterra system (3.9) is given by using a relation (2.22) as

where  is the simulation time,
is the simulation time,  , for
, for  , and (
, and ( ,
,  ) is the start point (initial conditions).
) is the start point (initial conditions).
Let us assume the following parameters of system (3.9):  and orders
and orders  and
and  , respectively.
, respectively.
Numerical solution (state plane trajectory) of the fractional-order Lotka-Volterra equations (3.9) with parameters:  , and initial conditions
, and initial conditions  ,
,  obtained by equations (3.10) for
obtained by equations (3.10) for  ,
,  , and
, and  is depicted in Figure 4. State plane trajectory for the integer-order Lotka-Volterra equations with the same parameters is depicted in Figure 5.
is depicted in Figure 4. State plane trajectory for the integer-order Lotka-Volterra equations with the same parameters is depicted in Figure 5.
Numerical solutions of fractional-order (
 ) Lotka-Volterra equations (
3.9) in state plane for simulation time 60 sec,
) Lotka-Volterra equations (
3.9) in state plane for simulation time 60 sec,  , and
, and  in (3.10).
in (3.10).
Numerical solutions of integer-order (
 ) Lotka-Volterra equations (
3.9
) in state plane for simulation time 60 sec,
) Lotka-Volterra equations (
3.9
) in state plane for simulation time 60 sec,  , and
, and  in (3.10).
in (3.10).
According to knowledge of author, there is no exact analytical solution of the fractional-order Lotka-Volterra equations, which could be compared with the numerical solution. The only possibility is to compare proposed numerical method with an approximate solution obtained via different numerical methods as for example homotopy perturbation method, variational iteration method, and so on.
4. Discussion
The proposed numerical method is also known as Euler method which is based on the Grünwald-Letnikov definition of the fractional derivative and can be used for numerical solution of the fractional differential equation even if the fractional-order derivative in differential equation is Caputo's or Riemann-Liouville type. It is based on the fact that for a wide class of functions, all three definitions of the fractional derivatives are equivalent [4].
Sometimes the Euler method is not accurate enough; it only has order one. We have to do a numerical analysis, which consists of not only the design of numerical methods, but also analysis of three main concepts.
-
(i)
Consistency and order. Tell us how well it approximates the solution, we can say, method is consistent if it has an order greater than 0. The method used in this article has order 1 and therefore it is consistent. Order is determined by generating function. Consistency is a necessary condition for convergence, but not sufficient.
-
(ii)
Convergence. It means whether the method approximates the solution, in other words, a numerical method is said to be convergent if the numerical solution
 approaches the exact solution
approaches the exact solution 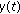 as the time step size
as the time step size  goes to 0. The method described in this article is convergent because the following condition is satisfied:
goes to 0. The method described in this article is convergent because the following condition is satisfied: (4.1)
(4.1)for
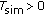 . For instance, we can observe a good result in comparison of exact solution and numerical solution shown in Figure 1. The time step was
. For instance, we can observe a good result in comparison of exact solution and numerical solution shown in Figure 1. The time step was  .
. -
(iii)
Stability and stiffness. It says whether errors are damped out. For some differential equations, application of standard methods exhibit instability in the solutions, though other methods may produce stable solutions. This behavior in the equation is described as stiffness. Method described in article provides a stable solution.
The numerical method (2.22) proposed for the initial value problem (2.21) holds all three above-mentioned conditions and can be used for solution of linear and nonlinear fractional differential equations. Based on performed experiments, we can consider what is the optimal choice of time step  in order to get maximum accuracy in the approximated solution for minimum computational cost. We have used the time steps
in order to get maximum accuracy in the approximated solution for minimum computational cost. We have used the time steps  ,
,  , and 0.0005. Numerical solutions show than we may accept the results obtained in this way. The size of the time step also depends on desired relative error in the solution.
, and 0.0005. Numerical solutions show than we may accept the results obtained in this way. The size of the time step also depends on desired relative error in the solution.
5. Conclusions
In this paper, we presented an effective numerical method and its application to solution of linear and nonlinear models of fractional order used in bioengineering applications. For some of them, Matlab functions [15, 17, 20] were also published. Here, three illustrative examples have been presented as well. It is worth to note that some other methods are also appropriate for solution of such kind of problem, for example predictor-corrector method [19], Podlubny's matrix approach [21, 22], quadrature formula approach [23], multistep method [24], and frequency (Oustaloup's) method [6], but it has some restrictions, especially for the fractional nonlinear models [25]. In further work, it is necessary to improve this method with proper mathematical analysis and exact determination of the time step size  .
.
References
Caponetto R, Dongola G, Fortuna L, Petráš I: Fractional Order Systems: Modeling and Control Applications. World Scientific, Singapore; 2010.
Hilfer R: Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Magin RL: Fractional Calculus in Bioengineering. Begell House; 2006.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York, NY, USA; 1974:xiii+234.
Oustaloup A: La Dérivation non Entière. Hermes, Paris, France; 1995.
Humbert P, Agarwal RP: Sur la fonction de Mittag-Leffler et quelques-unes de ses généralisations. Bulletin des Sciences Mathématiques 1953, 77: 180-185.
Gorenflo R: Fractional calculus: some numerical methods. In Fractals and Fractional Calculus in Continuum Mechanics, CISM Courses and Lectures. Volume 378. International Centre for Mechanical Sciences, Udine, Italy; 1996:277-290.
Lubich Ch: Discretized fractional calculus. SIAM Journal on Mathematical Analysis 1986,17(3):704-719. 10.1137/0517050
Barbosa RS, Tenreiro Machado JA, Silva MF: Time domain design of fractional differintegrators using least-squares. Signal Processing 2006,86(10):2567-2581. 10.1016/j.sigpro.2006.02.005
Dorčák L', Petráš I, Terpák J, Zborovjan M: Comparison of the methods for discrete approximation of the fractional-order operator. Acta Montanistica Slovaca 2003,8(4):236-239.
Vinagre BM, Podlubny I, Hernández A, Feliu V: Some approximations of fractional order operators used in control theory and applications. Fractional Calculus & Applied Analysis 2000,3(3):231-248.
Vinagre BM, Chen YQ, Petráš I: Two direct Tustin discretization methods for fractional-order differentiator/integrator. Journal of the Franklin Institute 2003,340(5):349-362. 10.1016/j.jfranklin.2003.08.001
Dorčák L': Numerical Models for the Simulation of the Fractional-Order Control Systems. The Academy of Science, Institute for Experimental Physics, Košice, Slovakia; 1994.
Petráš I, Magin RL: Numerical solution of two compartmental biological system model. In Proceedings of the 4th IFAC Workshop on Fractional Differentiation and Its Applications, October 2010, Badajoz, Spain. University of Extremadura;
Magin R, Feng X, Baleanu D: Solving the fractional order Bloch equation. Concepts in Magnetic Resonance A 2009,34(1):16-23.
Petráš I: Modeling and numerical analysis of fractional-order Bloch equations. Computers and Mathematics with Applications 2011,61(2):341-356. 10.1016/j.camwa.2010.11.009
Webb A: Introduction to Biomedical Imaging. John Wiley & Sons, New York, NY, USA; 2003.
Ahmed E, El-Sayed AMA, El-Saka HAA: Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. Journal of Mathematical Analysis and Applications 2007,325(1):542-553. 10.1016/j.jmaa.2006.01.087
Petráš I: Fractional Order Chaotic Systems (Matlab toolbox). MathWorks, Inc., FileExchange, 2010, http://www.mathworks.com/matlabcentral/fileexchange/27336
Podlubny I: Matrix approach to discrete fractional calculus. Fractional Calculus & Applied Analysis 2000,3(4):359-386.
Podlubny I, Chechkin A, Skovranek T, Chen Y, Vinagre Jara BM: Matrix approach to discrete fractional calculus. II. Partial fractional differential equations. Journal of Computational Physics 2009,228(8):3137-3153. 10.1016/j.jcp.2009.01.014
Diethelm K: An algorithm for the numerical solution of differential equations of fractional order. Electronic Transactions on Numerical Analysis 1997, 5: 1-6.
Lubich Ch: Fractional linear multistep methods for Abel-Volterra integral equations of the first kind. IMA Journal of Numerical Analysis 1987,7(1):97-106. 10.1093/imanum/7.1.97
Tavazoei MS, Haeri M: Limitations of frequency domain approximation for detecting chaos in fractional order systems. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1299-1320. 10.1016/j.na.2007.06.030
Acknowledgment
This work was supported in part by the Slovak Grant Agency for Science under Grants VEGA: 1/0390/10, 1/0497/11, 1/0746/11, Grants APVV-0040-07 and SK-PL-0052-09.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Petráš, I. An Effective Numerical Method and Its Utilization to Solution of Fractional Models Used in Bioengineering Applications. Adv Differ Equ 2011, 652789 (2011). https://doi.org/10.1155/2011/652789
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/652789

 , and
, and  in (3.6).
in (3.6).
 ) Bloch (3. 7) in state space for simulation time 1 sec
) Bloch (3. 7) in state space for simulation time 1 sec  , and
, and  in (3.8).
in (3.8).
 ) Bloch equations (3.7) in state space for simulation time
) Bloch equations (3.7) in state space for simulation time
 sec,
sec,
 , and
, and
 in (3.8).
in (3.8).


 approaches the exact solution
approaches the exact solution 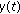 as the time step size
as the time step size  goes to 0. The method described in this article is convergent because the following condition is satisfied:
goes to 0. The method described in this article is convergent because the following condition is satisfied:
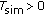 . For instance, we can observe a good result in comparison of exact solution and numerical solution shown in Figure
. For instance, we can observe a good result in comparison of exact solution and numerical solution shown in Figure  .
.