- Research Article
- Open access
- Published:
Existence of Solutions to Fractional Mixed Integrodifferential Equations with Nonlocal Initial Condition
Advances in Difference Equations volume 2011, Article number: 690653 (2011)
Abstract
We study the existence and uniqueness theorem for the nonlinear fractional mixed Volterra-Fredholm integrodifferential equation with nonlocal initial condition  , where
, where  ,
,  , and
, and  is a given function. We point out that such a kind of initial conditions or nonlocal restrictions could play an interesting role in the applications of the mentioned model. The results obtainded are applied to an example.
is a given function. We point out that such a kind of initial conditions or nonlocal restrictions could play an interesting role in the applications of the mentioned model. The results obtainded are applied to an example.
1. Introduction
Recently it have been proved that the differential models involving nonlocal derivatives of fractional order arise in many engineering and scientific disciplines as the mathematical modeling of systems and processes in many fields, for instance, physics, chemistry, aerodynamics, electrodynamics of complex medium, polymer rheology, and so forth (see [1–6]). In fact, such models can be considered as an efficient alternative to the classical nonlinear differential models to simulate many complex processes (see [7]). For instance, fractional differential equations are an excellent tool to describe hereditary properties of viscoelastic materials and, in general, to simulate the dynamics of many processes on anomalous media. Theory of fractional differential equations has been extensively studied by several authors as Delbosco and Rodino [8], Kilbas et al. [6], Lakshmikantham et al. [9–11], and also see [2, 12–16].
Recently Mophou and N'Guérékata [17], studied the Cauchy problem with nonlocal conditions

in general Banach space  with
with  , and
, and  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup of bounded linear operators. By means of the Krasnoselskii's Theorem, existence of solutions was also obtained.
-semigroup of bounded linear operators. By means of the Krasnoselskii's Theorem, existence of solutions was also obtained.
Subsequently several authors have investigated the problem for different types of nonlinear differential equations and integrodifferential equations including functional differential equations in Banach spaces.
Very recently N'Guérékata [2, 18] discussed the existence of solutions of fractional abstract differential equations with nonlocal initial condition. The nonlocal Cauchy problem is discussed by authors in [15] using the fixed-point concepts. Tidke [19] studied the nonfractional mixed Volterra-Fredholm integrodifferential equations with nonlocal conditions using Leray-Schauder Theorem.
Motivated by the above mentioned works in this manuscript we discuss the existence and the uniqueness of the solution for the following fractional integrodifferential equation with nonlocal integral initial condition in Banach Space:

where  ,
,  ,
,  ,
,  ,
,  is a continuous function on
is a continuous function on  with values in the Banach space
with values in the Banach space  and
and  , and
, and  ,
,  , and
, and  are continuous
are continuous  -valued functions. Here
-valued functions. Here  , and
, and  . The operator
. The operator  denotes the Caputo fractional derivative of order
denotes the Caputo fractional derivative of order  .
.
For the sake of the shortness let

The paper is organized as follows. In Section 2, some definitions, lemmas and preliminary results are introduced to be used in the sequel. Section 3 will involve the assumptions, main results and proofs of existence problem of (1.2), together with a nonlocal initial condition. Finally an example is presented.
2. Preliminaries
Let  be a real Banach space and
be a real Banach space and  the zero element of
the zero element of  . Let
. Let  be the Banach space of measurable functions
be the Banach space of measurable functions  which are Lebesgue integrable, equipped with the norm
which are Lebesgue integrable, equipped with the norm  . We will use the following notation
. We will use the following notation  and
and . A function
. A function  is called a solution of (1.2) if it satisfies (1.2).
is called a solution of (1.2) if it satisfies (1.2).
Definition 2.1.
A real function  is said to be in the space
is said to be in the space  if there exists a real number
if there exists a real number  , such that
, such that  , where
, where  , while
, while  is said to be in the space
is said to be in the space  if and only if
if and only if  .
.
Definition 2.2.
The fractional (arbitrary) order Riemann-Liouville integral (on the right and on the left) of the function  of order
of order  is defined by
is defined by

where  is the Gamma function of Euler.
is the Gamma function of Euler.
When  , we write
, we write  , where
, where  for
for  ,
,  for
for  , and
, and  represents the Convolution of Laplace. Then, it is well known that
represents the Convolution of Laplace. Then, it is well known that  as
as  , where
, where  is the Delta function.
is the Delta function.
Definition 2.3.
The Riemann-Liouville fractional integral operator of order  , of a function
, of a function  is defined as
is defined as

Definition 2.4.
The Caputo's derivative of fractional order  for a suitable function
for a suitable function  is defined by
is defined by

where  denotes the integer part of real number
denotes the integer part of real number  .
.
It is obvious that the Caputo's derivative of a constant is equal to 0.
Lemma 2.5.
Let  and
and  . Then
. Then

Lemma 2.6.
If  for
for  , and if
, and if  satisfies
satisfies  for
for  and
and  , then
, then

Proof.
A direct computation shows

Theorem 2.7 (Krasnoselkii).
Let  be a Banach space, let
be a Banach space, let  be a bounded closed convex subset of
be a bounded closed convex subset of  and let
and let  ,
,  be maps of
be maps of  into
into  such that
such that  for every pair
for every pair  . If A is completely continuous and B is a contraction then the equation
. If A is completely continuous and B is a contraction then the equation  has a solution on S.
has a solution on S.
3. Main Results
We assume the following.
-
(A1)
If
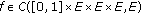 and a nonnegative, bounded
and a nonnegative, bounded 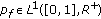 , there exist
, there exist 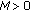 ,
, 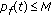 for
for  such that
such that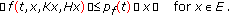 (3.1)
(3.1) -
(A2)
There exist positive constants
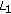 ,
, 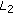 , and
, and 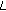 such that
such that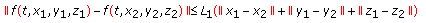 (3.2)
(3.2) -
for
all
 ,
,  , and
, and 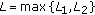 .
. -
(A3)
There exist positive constants
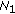 ,
, 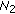 , and
, and  such that
such that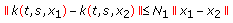 (3.3)
(3.3) -
for
all
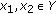 ,
,  , and
, and 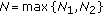 .
. -
(A4)
There exist positive constants
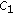 ,
, 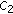 , and
, and  such that
such that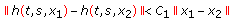 (3.4)
(3.4) -
for
all
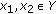 ,
, 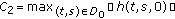 , and
, and 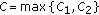 .
. -
(A5)
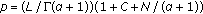 is such that
is such that 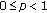 .
.
Firstly, we obtain the following lemmas to prove the main results on the existence of solutions to (1.2).
Lemma 3.1.
If (A1) holds with  , then the problem (1.2) is equivalent to the following equation:
, then the problem (1.2) is equivalent to the following equation:

Proof.
By Lemma 2.5 and (1.2), we have

Therefore,

So,

and then

Conversely, if  is a solution of (3.5), then for every
is a solution of (3.5), then for every  , according to Definition 2.4 we have
, according to Definition 2.4 we have

It is obvious that  . This completes the proof.
. This completes the proof.
Lemma 3.2.
If (A3) and (A4) are satisfied,  ,
,  are defined in (A), then the conditions
are defined in (A), then the conditions

are satisfied for any  , and
, and  .
.
Proof.
By (A3), we have

On the other hand,

Similarly, for the other conditions, we use assumption (A4), to get

Theorem 3.3.
If (A1)–(A5) are satisfied, then the fractional integrodifferential equation (1.2) has a unique solution continuous in  .
.
Proof.
We use the Banach contraction principle to prove the existence and uniqueness of the solution to (1.2). Let  , where
, where  and define the operator
and define the operator  on the Banach space
on the Banach space  by
by

Firstly, we show that the operator  maps
maps  into itself. By using (A1) and triangle inequality, we have
into itself. By using (A1) and triangle inequality, we have

Now, if (A2) is satisfied, then

Using Lemma 3.2 and (A3), we have

if  , we have
, we have

Thus  . Next, we prove that
. Next, we prove that  is a contraction mapping. For this, let
is a contraction mapping. For this, let  . Applying (A2), we have
. Applying (A2), we have

then using (A3), (A4) and Lemma 3.2, one gets

where  =
=  depends on the parameter of the problem. Therefore
depends on the parameter of the problem. Therefore  has a unique fixed-point
has a unique fixed-point  , which is a solution of (3.5), and hence is a solution of (1.2).
, which is a solution of (3.5), and hence is a solution of (1.2).
Theorem 3.4.
Assume (A1)–(A4) holds. If  , then (1.2) has at least one solution on
, then (1.2) has at least one solution on  .
.
Proof.
Choose  and consider
and consider  . Now define on
. Now define on  the operators
the operators  by
by

Let us observe that if  then
then  . Indeed it is easy to check the inequality
. Indeed it is easy to check the inequality

We can easily show that that  is a contraction mapping. Let
is a contraction mapping. Let  . Then
. Then

where  depends only on the parameter of the problem and hence
depends only on the parameter of the problem and hence  is contraction. Since
is contraction. Since  is continuous, then
is continuous, then  is continuous in view of (A1). Let us now note that
is continuous in view of (A1). Let us now note that  is uniformly bounded on
is uniformly bounded on  . This follows from the inequality
. This follows from the inequality

Now let us prove that  is equicontinuous.
is equicontinuous.
Let  and
and  . Using the fact that
. Using the fact that  is bounded on the compact set
is bounded on the compact set  (thus
(thus  , we will get
, we will get

which does not depend on  . So
. So  is relatively compact. By the Arzela-Ascoli Theorem,
is relatively compact. By the Arzela-Ascoli Theorem,  is compact. We now conclude the result of the theorem based on the Krasnoselkii's theorem above.
is compact. We now conclude the result of the theorem based on the Krasnoselkii's theorem above.
4. Example
Consider the following fractional integrodifferential equation:

where  . Take
. Take  . Set
. Set  ,
,  ,
,  ,
,  . Then it is clear that
. Then it is clear that

So, (A1) is satisfied. Let  and
and  . Then we have
. Then we have

Hence the conditions (A1)–(A4) hold with  ,
,  ,
,  ,
,  . Choose
. Choose  and
and  . Indeed
. Indeed

Further (A5) is satisfied by a suitable choice of  . Then by Lemma 3.2 the problem (1.2) has a unique solution on [0,1].
. Then by Lemma 3.2 the problem (1.2) has a unique solution on [0,1].
References
Caputo M: Linear models of dissipation whose q is almost frequently independent, part II. Journal of the Royal Astronomical Society 1967, 13: 529-539.
N'Guérékata GM: A Cauchy problem for some fractional abstract differential equation with non local conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1873-1876. 10.1016/j.na.2008.02.087
He J-H: Some applications of nonlinear fractional differential equations and their approximation. Bulletin of Science, Technology & Society 1999,15(2):86-90.
He J-H: Approximate analytical solution for seepage flow with fractional derivatives in porous media. Computer Methods in Applied Mechanics and Engineering 1998,167(1-2):57-68. 10.1016/S0045-7825(98)00108-X
Hilfer R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations. Volume 204. North-Holland Mathematics Studies; 2006.
Bonilla B, Rivero M, Rodríguez-Germá L, Trujillo JJ: Fractional differential equations as alternative models to nonlinear differential equations. Applied Mathematics and Computation 2007,187(1):79-88. 10.1016/j.amc.2006.08.105
Delbosco D, Rodino L: Existence and uniqueness for a nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 1996,204(2):609-625. 10.1006/jmaa.1996.0456
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Devi JV: Theory of fractional differential equations in a Banach space. European Journal of Pure and Applied Mathematics 2008,1(1):38-45.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Agarwal RP, Lakshmikantham V, Nieto JJ: On the concept of solution for fractional differential equations with uncertainty. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):2859-2862. 10.1016/j.na.2009.11.029
Anguraj A, Karthikeyan P, N'Guérékata GM: Nonlocal Cauchy problem for some fractional abstract integrodifferential equations in Banach space. Communications in Mathematical Analysis 2009,55(6):1-6.
Balachandran K, Park JY: Nonlocal Cauchy problem for abstract fractional semilinear evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4471-4475. 10.1016/j.na.2009.03.005
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. Journal of Mathematical Analysis and Applications 1991,162(2):494-505. 10.1016/0022-247X(91)90164-U
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
N'Guérékata GM: Existence and uniqueness of an integral solution to some Cauchy problem with nonlocal conditions. In Differential & Difference Equations and Applications. Hindawi, New York, NY, USA; 2006:843-849.
Tidke HL: Existence of global solutions to nonlinear mixed Volterra-Fredholm integrodifferential equations with nonlocal conditions. Electronic Journal of Differential Equations 2009,2009(55):-7.
Acknowledgment
This paper has been partially supported by MICINN (project MTM2010-16499) to which the authors are very thankful.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Anguraj, A., Karthikeyan, P. & Trujillo, J.J. Existence of Solutions to Fractional Mixed Integrodifferential Equations with Nonlocal Initial Condition. Adv Differ Equ 2011, 690653 (2011). https://doi.org/10.1155/2011/690653
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/690653
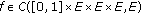 and a nonnegative, bounded
and a nonnegative, bounded 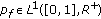 , there exist
, there exist 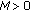 ,
, 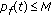 for
for  such that
such that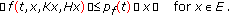
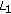 ,
, 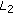 , and
, and 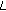 such that
such that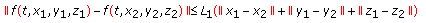
 ,
,  , and
, and 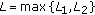 .
.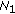 ,
, 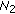 , and
, and  such that
such that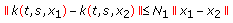
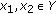 ,
,  , and
, and 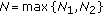 .
.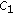 ,
, 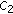 , and
, and  such that
such that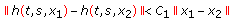
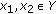 ,
, 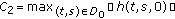 , and
, and 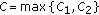 .
.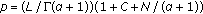 is such that
is such that 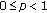 .
.