- Research Article
- Open access
- Published:
On the Existence of Equilibrium Points, Boundedness, Oscillating Behavior and Positivity of a SVEIRS Epidemic Model under Constant and Impulsive Vaccination
Advances in Difference Equations volume 2011, Article number: 748608 (2011)
Abstract
This paper discusses the disease-free and endemic equilibrium points of a SVEIRS propagation disease model which potentially involves a regular constant vaccination. The positivity of such a model is also discussed as well as the boundedness of the total and partial populations. The model takes also into consideration the natural population growing and the mortality associated to the disease as well as the lost of immunity of newborns. It is assumed that there are two finite delays affecting the susceptible, recovered, exposed, and infected population dynamics. Some extensions are given for the case when impulsive nonconstant vaccination is incorporated at, in general, an aperiodic sequence of time instants. Such an impulsive vaccination consists of a culling or a partial removal action on the susceptible population which is transferred to the vaccinated one. The oscillatory behavior under impulsive vaccination, performed in general, at nonperiodic time intervals, is also discussed.
1. Introduction
Important control problems nowadays related to Life Sciences are the control of ecological models like, for instance, those of population evolution (Beverton-Holt model, Hassell model, Ricker model, etc. [1–5]) via the online adjustment of the species environment carrying capacity, that of the population growth or that of the regulated harvesting quota as well as the disease propagation via vaccination control. In a set of papers, several variants and generalizations of the Beverton-Holt model (standard time-invariant, time-varying parameterized, generalized model or modified generalized model) have been investigated at the levels of stability, cycle-oscillatory behavior, permanence, and control through the manipulation of the carrying capacity (see, e.g., [1–5]). The design of related control actions has been proved to be important in those papers at the levels, for instance, of aquaculture exploitation or plague fighting. On the other hand, the literature about epidemic mathematical models is exhaustive in many books and papers. A nonexhaustive list of references is given in this manuscript, compare [6–14] (see also the references listed therein). The sets of models include the most basic ones, [6, 7].
-
(i)
SI-models where not removed-by-immunity population is assumed. In other words, only susceptible and infected populations are assumed.
-
(ii)
SIR-models, which include susceptible, infected, and removed-by-immunity populations.
-
(iii)
SEIR-models where the infected populations is split into two ones (i.e., the "infected" which incubate the disease but do not still have any disease symptoms and the "infectious" or "infective" which do exhibit the external disease symptoms).
The three above models have two possible major variants, namely, the so-called "pseudomass action models," where the total population is not taken into account as a relevant disease contagious factor or disease transmission power, and the so-called "true-mass action models", where the total population is more realistically considered as being an inverse factor of the disease transmission rates. There are other many variants of the above models, for instance, including vaccination of different kinds: constant [8], impulsive [12], discrete-time, and so forth, incorporating point or distributed delays [12, 13], oscillatory behaviors [14], and so forth. On the other hand, variants of such models become considerably simpler for the disease transmission among plants [6, 7]. Some generalizations involve the use of a mixed regular continuous-time/impulsive vaccination control strategies for generalized time-varying epidemic model which is subject to point and distributed time-varying delays, [12, 13, 15–17]. Other well-known types of epidemic models are the so-called SVEIRS epidemic models which incorporate the dynamics of a vaccinated population, and the "infected" population without external symptoms of the SEIR-type models is replaced with an "exposed" population subject to a certain dynamics, [18, 19]. Thus, in the context of SVEIRS models, the infected and infectious populations of the SEIR models are joined in a single "infected" population  while there is an exposed population
while there is an exposed population  present in the model. In this paper, we focus on the existence and some properties of disease-free and endemic equilibrium points of a SVEIRS model subject to an eventual constant regular vaccination rather than to an impulsive vaccination type. Some issues about boundedness and positivity of the model are also investigated. The following impulsive-free SVEIRS epidemic model, of a modified true-mass action type, with regular constant vaccination is being firstly considered
present in the model. In this paper, we focus on the existence and some properties of disease-free and endemic equilibrium points of a SVEIRS model subject to an eventual constant regular vaccination rather than to an impulsive vaccination type. Some issues about boundedness and positivity of the model are also investigated. The following impulsive-free SVEIRS epidemic model, of a modified true-mass action type, with regular constant vaccination is being firstly considered





where  , and
, and  are, respectively, the susceptible, vaccinated, exposed, infected (or infective or infectious), and recovered populations,
are, respectively, the susceptible, vaccinated, exposed, infected (or infective or infectious), and recovered populations,  is the total population being the sum of the above ones, and
is the total population being the sum of the above ones, and  is a constant vaccination action. There are potential latent and immune periods denoted by
is a constant vaccination action. There are potential latent and immune periods denoted by  and
and  , respectively, which are internal delays in the dynamic system (1.1)–(1.5), and
, respectively, which are internal delays in the dynamic system (1.1)–(1.5), and  is the natural birth rate and death rate of the population. The parameter
is the natural birth rate and death rate of the population. The parameter  takes into account a vaccination action on newborns which decreases the incremental susceptible population through time,
takes into account a vaccination action on newborns which decreases the incremental susceptible population through time,  is the average rate for vaccines to obtain immunity and move into recovered population, and
is the average rate for vaccines to obtain immunity and move into recovered population, and  (disease transmission constant) and
(disease transmission constant) and  are, respectively, average numbers for contacts of an infective with a susceptible and an infective with a vaccinated individual per unit of time, [18]. The periodic impulsive, rather than regular, vaccination action proposed in [18, 19], can be got from (1.1)–(1.5) with
are, respectively, average numbers for contacts of an infective with a susceptible and an infective with a vaccinated individual per unit of time, [18]. The periodic impulsive, rather than regular, vaccination action proposed in [18, 19], can be got from (1.1)–(1.5) with  while adding either corresponding "culling" action, or, alternatively, a less drastic "partial removal of susceptible from the habitat" action. This implies in practical terms to put in quarantine a part of the susceptible population so as to minimize the effects of the disease propagation what corresponds with a population decrease of the susceptible in the habitat under study and a parallel increase of the vaccinated populations at times being an integer multiple of some prefixed period
while adding either corresponding "culling" action, or, alternatively, a less drastic "partial removal of susceptible from the habitat" action. This implies in practical terms to put in quarantine a part of the susceptible population so as to minimize the effects of the disease propagation what corresponds with a population decrease of the susceptible in the habitat under study and a parallel increase of the vaccinated populations at times being an integer multiple of some prefixed period  . This paper investigate through Sections 2–4 the existence and uniqueness of the delay-free and endemic equilibrium points as well as the positivity and boundedness of the state-trajectory solutions under arbitrary nonnegative initial conditions and optional constant vaccination. Some generalized extensions concerning this model are given in Section 5 by using aperiodic impulsive vaccination with time-varying associated gains, in general, and investigating the state-trajectory solution properties. This impulsive vaccinations strategy will be performed as follows at a sequence of time instants
. This paper investigate through Sections 2–4 the existence and uniqueness of the delay-free and endemic equilibrium points as well as the positivity and boundedness of the state-trajectory solutions under arbitrary nonnegative initial conditions and optional constant vaccination. Some generalized extensions concerning this model are given in Section 5 by using aperiodic impulsive vaccination with time-varying associated gains, in general, and investigating the state-trajectory solution properties. This impulsive vaccinations strategy will be performed as follows at a sequence of time instants  ran in general at a nonperiodic "in-between" sampling interval sequence:
ran in general at a nonperiodic "in-between" sampling interval sequence:

Examples are provided in Section 6. It has to be pointed out that other variants of epidemic models have been recently investigated as follows. In [20], a mixed regular and impulsive vaccination action is proposed for a SEIR epidemic mode model which involves also mixed point and distributed delays. In [21], an impulsive vaccination strategy is discussed for a SVEIR epidemic model whose latent period is a point delay while the existence of an immune period is not assumed. In [22], a latent period is introduced in the susceptible population of a SIR epidemic model with saturated incidence rate. The disease-free equilibrium point results to be locally asymptotically stable if the reproduction number is less than unity while the endemic equilibrium point is locally asymptotically stable if such a number exceeds unity.
2. The Disease-Free Equilibrium Point
The potential existence of a disease-free equilibrium point is now discussed which asymptotically removes the disease if  .
.
Theorem 2.1.
Assume that  . Then, the disease-free equilibrium point
. Then, the disease-free equilibrium point  fulfils
fulfils

which imply the following further constraints:

Two particular disease-free equilibrium points are  ,
,  if
if  , and
, and  ,
,  ,
,  ,
,  if
if  .
.
If  , then there is no disease-free equilibrium points.
, then there is no disease-free equilibrium points.
Proof.
Any existing equilibrium points are calculated as follows by zeroing (1.1), (1.2), (1.4), and (1.5) and making (1.3) identical to an equilibrium value  what leads to:
what leads to:




The disease-free equilibrium point satisfies the constraints

The proof follows directly from the above equations.
Remark 2.2.
Note that if  , then
, then  . Note also that if
. Note also that if  , as in the particular case of impulsive-free SVEIRS model obtained from that discussed in [18, 19], then the disease-free equilibrium satisfies
, as in the particular case of impulsive-free SVEIRS model obtained from that discussed in [18, 19], then the disease-free equilibrium satisfies  ,
,  . In such a case, the model can be ran out with population normalized to unity.
. In such a case, the model can be ran out with population normalized to unity.
Assertion 1.
Assume that  . Then,
. Then,

where  .
.
Proof.
Note from Theorem 2.1 that the disease-free equilibrium point satisfies from simple direct calculations that

since  what also yields
what also yields  , that is,
, that is,  .
.
Note that the exposed population at the equilibrium defined by (1.3) can be equivalently described by a differential equation obtained by applying the Leibniz differentiation rule under the integral symbol to yield

The local asymptotic stability of the disease-free equilibrium point is guaranteed by that of the linearized incremental system about it. The linearized model about the equilibrium becomes to be defined from (1.1), (1.2), (2.10) and (1.4), (1.5) by the state vector  which satisfies the differential system
which satisfies the differential system

where, after using the identities in Theorem 2.1 related to the equilibrium point and provided that Assertion 1 holds, one gets

where  is a real constant, and
is a real constant, and


and the matrices  and
and  are entry-wise defined by
are entry-wise defined by

with all the remaining entries being zero. The following inequalities apply for equivalent norms of either vectors or vector-induced norms of matrices  of dimension or, respectively, order
of dimension or, respectively, order  :
:

Thus, one gets from the above inequalities (2.16) that

where

Note from (2.18) that  for a given
for a given  and any given positive real constant
and any given positive real constant  if
if  and
and  , if positive, are small enough such that, equivalently,
, if positive, are small enough such that, equivalently,

Thus, one gets from (2.17)–(2.19) that

On the other hand, we can use from L'Hopital rule the following limit relations in the entries  and
and  of the matrix
of the matrix  :
:

if the remaining parameters remain finite and then  and
and  from Theorem 2.1. By continuity with respect to parameters, for any sufficiently large
from Theorem 2.1. By continuity with respect to parameters, for any sufficiently large  , there exist
, there exist  with
with  as
as  such that for
such that for  ,
,

and, one gets from (2.14),

and for  being large enough such that it satisfies
being large enough such that it satisfies

with  being some existing real positive constant, depending on the vaccination constant
being some existing real positive constant, depending on the vaccination constant  , such that
, such that  , it follows from inspection of (2.22), (2.23) that
, it follows from inspection of (2.22), (2.23) that  . Using again (2.16), (2.17), it follows that the following close constraint to (2.19) for large enough
. Using again (2.16), (2.17), it follows that the following close constraint to (2.19) for large enough  :
:

guarantees

where

On the other hand, note that the linearized system (2.11)–(2.17) is asymptotically stable if and only if

which is guaranteed under the two conditions below:
-
(1)
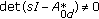 , for all
, for all  , equivalently,
, equivalently, 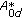 is a stability matrix
is a stability matrix -
(2)
the
 -matrix measure
-matrix measure  of
of 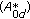 is negative, and, furthermore, the following constraint holds
is negative, and, furthermore, the following constraint holds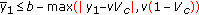 (2.29)
(2.29)which guarantees the above stability Condition 2 via (2.26), (2.27), and (2.13)
 (2.30)
(2.30)
The following result is proven from Theorem 2.1, by taking into account the above asymptotic stability conditions for the linearized incremental system about the disease-free equilibrium point, which imply that of the nonlinear one (1.1)–(1.5) about the equilibrium point, and the related former discussion.
Theorem 2.3.
Assume that  . Then, there is a sufficiently large
. Then, there is a sufficiently large  such that the disease-free equilibrium point is locally asymptotically stable for any constant vaccination
such that the disease-free equilibrium point is locally asymptotically stable for any constant vaccination  and a sufficiently small amount
and a sufficiently small amount  , a sufficiently small delay
, a sufficiently small delay  and a sufficiently small difference delay
and a sufficiently small difference delay  (this being applicable if
(this being applicable if  ) such that (2.30) holds.
) such that (2.30) holds.
Note that the statement of Theorem 2.3 guarantees the local stability of the disease-free equilibrium point under its existence condition of Theorem 2.1 requiring  .
.
3. The Existence of Endemic Equilibrium Points, Uniqueness Issues, and Some Related Characterizations
The existence of endemic equilibrium points which keep alive the disease propagation is now discussed. It is proven that there is a unique equilibrium point with physical meaning since all the partial populations are nonnegative.
Theorem 3.1.
Assume that  . Then, the following properties hold.
. Then, the following properties hold.
-
(i)
Assume that
 for
for  and
and  for
for 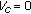 . Thus, there is at least one endemic equilibrium point at which the susceptible, vaccinated, infected, exposed, and recovered populations are positive and the vaccinated population is zero if and only if
. Thus, there is at least one endemic equilibrium point at which the susceptible, vaccinated, infected, exposed, and recovered populations are positive and the vaccinated population is zero if and only if 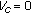 (i.e., in the absence of vaccination action). Furthermore, such an equilibrium point satisfies the constraints
(i.e., in the absence of vaccination action). Furthermore, such an equilibrium point satisfies the constraints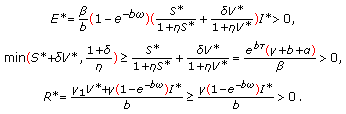 (3.1)
(3.1) -
(ii)
If the disease transmission constant is small enough satisfying
 for
for 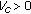 , and
, and  for
for 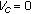 , then there is no reachable endemic equilibrium point.
, then there is no reachable endemic equilibrium point.
Proof.
The endemic equilibrium point is calculated as follows:


with


(since, otherwise, the above disease-free equilibrium point would be considered).
 since, otherwise, the following contradiction would follow:
since, otherwise, the following contradiction would follow:

 if and only if
if and only if  , since otherwise for
, since otherwise for  and
and  , it would follow that
, it would follow that  , what is only possible in the disease-free equilibrium if the total population is extinguished, is a contradiction at the endemic point
, what is only possible in the disease-free equilibrium if the total population is extinguished, is a contradiction at the endemic point

Remark 3.2.
Note that if  , then it follows from (1.3) and (2.4) that
, then it follows from (1.3) and (2.4) that  , for all
, for all so that the SVEIRS model (1.1)–(1.5) becomes a simpler SVIRS one without specification of the exposed population dynamics.
so that the SVEIRS model (1.1)–(1.5) becomes a simpler SVIRS one without specification of the exposed population dynamics.
Remark 3.3.
Note that, under the constraints in Theorem 3.1(ii) for  , if there is no reachable endemic equilibrium point because
, if there is no reachable endemic equilibrium point because  , then the solution trajectory of (1.1)–(1.5) can only either converge to the disease-free equilibrium point provided that it is at least locally asymptotically stable or to be bounded converging or not to an oscillatory solution or to diverge to an unbounded total population depending on the values of the parameterization of the model (1.1)–(1.5). Note that the endemic-free disease transmission constant upper-bound
, then the solution trajectory of (1.1)–(1.5) can only either converge to the disease-free equilibrium point provided that it is at least locally asymptotically stable or to be bounded converging or not to an oscillatory solution or to diverge to an unbounded total population depending on the values of the parameterization of the model (1.1)–(1.5). Note that the endemic-free disease transmission constant upper-bound  increases as
increases as  and
and  increase and also as
increase and also as  decreases.
decreases.
If  , then it follows from Theorem 3.1 that there exist positive constants
, then it follows from Theorem 3.1 that there exist positive constants  ,
,  ,
,  ,
,  , and
, and  satisfying
satisfying  such that the endemic equilibrium points, if any, satisfy the constraints
such that the endemic equilibrium points, if any, satisfy the constraints

so that one gets from (3.3)–(3.7) that


if  , otherwise, then only the upper-bounding constraint holds in (3.10)
, otherwise, then only the upper-bounding constraint holds in (3.10)


Equation (3.9) is equivalent, since  at the endemic equilibrium point, to
at the endemic equilibrium point, to

Equation (3.11) is equivalent to

Equation (3.14) is an algebraic equation of real coefficients of the form  with
with  . Such an equation has two positive real roots if
. Such an equation has two positive real roots if  ,
,  and
and  and one positive real root if
and one positive real root if  and
and  . Thus, since there is a nonzero susceptible population at an endemic equilibrium point, then either (3.15) below holds
. Thus, since there is a nonzero susceptible population at an endemic equilibrium point, then either (3.15) below holds

or, alternatively,

with  hold. On the other hand, (3.12) is equivalent to
hold. On the other hand, (3.12) is equivalent to

where  so that (3.17) is of the form specifically as follows:
so that (3.17) is of the form specifically as follows:

Now, the same reasoning as that used for the susceptible endemic equilibrium component is applied to (3.18) to conclude that, since there is a nonzero vaccinated population for at most two endemic equilibrium points with  , then
, then

which is obtained from (3.2), and either

or,  in (3.18). The uniqueness of the endemic equilibrium point with all partial populations being nonnegative for all time is now proven as follows. First, define auxiliary variables
in (3.18). The uniqueness of the endemic equilibrium point with all partial populations being nonnegative for all time is now proven as follows. First, define auxiliary variables

Thus, since  , (3.14) can be rewritten as follows:
, (3.14) can be rewritten as follows:

If such an equation has two positive real roots for the susceptible equilibrium (implicitly depending on  , then either
, then either  or
or  what is impossible and leads to a contradiction. Then, there is a unique nonnegative susceptible population
what is impossible and leads to a contradiction. Then, there is a unique nonnegative susceptible population  at the two potentially existing endemic equilibrium points provided that the total population
at the two potentially existing endemic equilibrium points provided that the total population  at the endemic equilibrium point is unique. Furthermore, simple inspection of the above equation implies strict positivity
at the endemic equilibrium point is unique. Furthermore, simple inspection of the above equation implies strict positivity  . On the other hand, it follows from Theorem 3.1, (3.5), that
. On the other hand, it follows from Theorem 3.1, (3.5), that  , which has a unique solution in
, which has a unique solution in  for a given
for a given  . Since there is a unique
. Since there is a unique  , then there is a unique
, then there is a unique  as a result. From (2.5) in the proof of Theorem 2.1, there is also a unique population at the infected population endemic equilibrium
as a result. From (2.5) in the proof of Theorem 2.1, there is also a unique population at the infected population endemic equilibrium  , then unique related exposed and recovered equilibrium populations
, then unique related exposed and recovered equilibrium populations  and
and  from (2.4) and (2.6), respectively. Thus, there is a unique endemic equilibrium point with all the partial populations being nonnegative. The above discussion concerning the existence of a unique endemic equilibrium point with all the partial populations being nonnegative is summarized as follows.
from (2.4) and (2.6), respectively. Thus, there is a unique endemic equilibrium point with all the partial populations being nonnegative. The above discussion concerning the existence of a unique endemic equilibrium point with all the partial populations being nonnegative is summarized as follows.
Theorem 3.4.
Assume that and that
and that  (the upper-bounding condition does not hold if
(the upper-bounding condition does not hold if  so that
so that  for some positive constants
for some positive constants  and
and  . If
. If  is unique at the endemic equilibrium then, there is a unique endemic equilibrium point with all the corresponding partial populations being positive, and the following parametrical constraints hold:
is unique at the endemic equilibrium then, there is a unique endemic equilibrium point with all the corresponding partial populations being positive, and the following parametrical constraints hold:

The constants  , and
, and  satisfy either (3.15), or (3.16), and the constraint
satisfy either (3.15), or (3.16), and the constraint  so that
so that  in (3.18).
in (3.18).
This result will be combined with some issues concerning the existence of limits of all the partial population at infinite time to conclude that there is a unique total population at the endemic equilibrium points so that, from Theorem 3.4, there is a unique endemic equilibrium point (see Remark 5.1 and Theorem 5.2 in Section 5).
4. About Infection Propagation and the Properties of Uniform Boundedness of the Total Population and Positivity of All the Partial Populations
This section discuses briefly the monotone increase of the infected population and the boundedness of the total population as well as the positivity of the model.
Theorem 4.1.
If the infection propagates through  with the infected population being monotone increasing, then
with the infected population being monotone increasing, then

Proof.
Note from (1.4) that for 

and if, furthermore,  for
for  , then
, then

Now, rewrite (1.3) in differential equivalent form by using Leibnitz's rule as follows:

Theorem 4.2.
Assume that  . Then, the following properties hold provided that the SVEIR epidemic model (1.1)–(1.5) has nonnegative solution trajectories of all the partial populations for all time:
. Then, the following properties hold provided that the SVEIR epidemic model (1.1)–(1.5) has nonnegative solution trajectories of all the partial populations for all time:
-
(i)
assume furthermore that
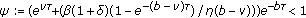 , then the total population is uniformly bounded for all time, irrespective of the susceptible and vaccinated populations, for any bounded initial conditions and
, then the total population is uniformly bounded for all time, irrespective of the susceptible and vaccinated populations, for any bounded initial conditions and (4.5)
(4.5) -
(ii)
assume that the disease transmission constant is large enough satisfying
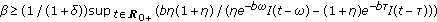 subject to
subject to  and
and 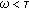 , then
, then 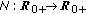 is monotone decreasing and of negative exponential order so that the total population exponentially extinguishes as a result.
is monotone decreasing and of negative exponential order so that the total population exponentially extinguishes as a result.
Proof.
Consider the SVEIRS model in differential form described by (1.1), (1.2), (1.4), (1.5), and (4.4). Summing up the five equations, one gets directly


since  ; for all
; for all  . Then,
. Then,

and Property (i) follows since  . Two cases are now discussed separately related to the proof of Property (ii).
. Two cases are now discussed separately related to the proof of Property (ii).
-
(a)
Note that if the solution trajectory is positive subject to
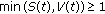 (equivalently if
(equivalently if  ), then
), then  (4.9)
(4.9)
so that one gets from (4.6)

with identically zero upper-bound in (4.10) holds for some  if and only if
if and only if  since
since  and
and

provided that  with
with  . Then,
. Then,  , for all
, for all  .
.
-
(b)
If
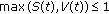 (equivalently, if
(equivalently, if  , then
, then  (4.12)
(4.12)
so that (4.10) still holds and the same conclusion arises. Thus, Property (ii) is proven.
A brief discussion about positivity is summarized in the next result.
Theorem 4.3.
Assume that  . Then, the SVEIRS epidemic model (1.1)–(1.5) is positive in the sense that no partial population is negative at any time if its initial conditions are nonnegative and the vaccinated population exceeds a certain minimum measurable threshold in the event that the recovered population is zero as follows:
. Then, the SVEIRS epidemic model (1.1)–(1.5) is positive in the sense that no partial population is negative at any time if its initial conditions are nonnegative and the vaccinated population exceeds a certain minimum measurable threshold in the event that the recovered population is zero as follows:  if
if  . The susceptible, vaccinated, exposed, and infected populations are nonnegative for all time irrespective of the above constraint. If, in addition, Theorem 4.2(i) holds, then all the partial populations of the SVEIRS model are uniformly bounded for all time.
. The susceptible, vaccinated, exposed, and infected populations are nonnegative for all time irrespective of the above constraint. If, in addition, Theorem 4.2(i) holds, then all the partial populations of the SVEIRS model are uniformly bounded for all time.
Proof.
First note that all the partial populations are defined by continuous-time differentiable functions from (1.1)–(1.5). Then, if any partial population is negative, it is zero at some previous time instant. Assume that  for
for  and
and  at some time instant
at some time instant  . Then, from (1.1)
. Then, from (1.1)

Thus,  . As a result,
. As a result,  cannot reach negative values at any time instant. Assume that
cannot reach negative values at any time instant. Assume that  for
for  and
and  at some time instant
at some time instant  . Then,
. Then,  from (1.2) so that
from (1.2) so that  . As a result,
. As a result,  cannot reach negative values at any time.
cannot reach negative values at any time.  for any time instant
for any time instant  from (1.3). Assume that
from (1.3). Assume that  for
for  and
and  at some time instant
at some time instant  . Then,
. Then,  from (1.4). As a result,
from (1.4). As a result,  cannot reach negative values at any time. Finally, assume that
cannot reach negative values at any time. Finally, assume that  for
for  and
and  at some time instant
at some time instant  . Thus,
. Thus,  from (1.5) if
from (1.5) if  . Thus, if
. Thus, if  when
when  , then all the partial populations are uniformly bounded, since they are nonnegative and the total population
, then all the partial populations are uniformly bounded, since they are nonnegative and the total population  is uniformly bounded from Theorem 4.2(i).
is uniformly bounded from Theorem 4.2(i).
It is discussed in the next section that if the two above theorems related to positivity and boundedness hold, then the solution trajectories converge to either the disease-free equilibrium point or to the endemic equilibrium point.
5. Solution Trajectory of the SVEIRS Model
The solution trajectories of the SVEIRS differential model (1.1)–(1.5) are given below.
Equation (1.1) yields

Equation (1.2) yields

Equation (1.3) is already in integral form. Equation (1.4) yields


Equation (1.5) yields

The asymptotic values of the partial populations can be calculated from (5.1)–(5.4) as time tends to infinity as follows provided that the involved right-hand-side integrals exist:

Remark 5.1.
If any of the above right-hand-side integrals with upper-limit  does not exist, then the corresponding limit of the involved partial population as time tends to infinity does not exist and, then, the limit value has to be replaced by the existing limit superior as time tends to infinity. Note that if Theorems 4.2 and 4.3 hold then all the limit values at infinity of the partial populations exist since the total population is uniformly bounded and all the partial populations are nonnegative for all time. A conclusion of this feature is that under positivity and boundedness of the solutions, all the partial populations of the impulsive-free SVEIRS model (1.1)–(1.5) have finite limits as time tends to infinity. As a result, all the trajectory solutions converge asymptotically either to the disease-free equilibrium point or to the endemic equilibrium point.
does not exist, then the corresponding limit of the involved partial population as time tends to infinity does not exist and, then, the limit value has to be replaced by the existing limit superior as time tends to infinity. Note that if Theorems 4.2 and 4.3 hold then all the limit values at infinity of the partial populations exist since the total population is uniformly bounded and all the partial populations are nonnegative for all time. A conclusion of this feature is that under positivity and boundedness of the solutions, all the partial populations of the impulsive-free SVEIRS model (1.1)–(1.5) have finite limits as time tends to infinity. As a result, all the trajectory solutions converge asymptotically either to the disease-free equilibrium point or to the endemic equilibrium point.
The considerations in Remark 5.1 are formally expressed as the subsequent important result by taking also into account the uniqueness of the infected population at any endemic equilibrium points, the uniqueness of the vaccinated population at such points (which follows from (3.12) and which implies the uniqueness of the total population at such an equilibrium endemic points (see Remark 5.1).
Theorem 5.2.
The following two properties hold.
-
(i)
The endemic equilibrium point is unique.
-
(ii)
Assume that Theorems 4.2 and 4.3 hold. Then, any solution trajectory of the SVEIRS impulsive-free vaccination model (1.1)–(1.5) generated for finite initial conditions converges asymptotically either to the disease-free equilibrium point or to the endemic equilibrium point as time tends to infinity.
Now, assume that the solution trajectory converges to some locally asymptotically stable equilibrium point  . The above equations ensure the existence of integrands
. The above equations ensure the existence of integrands  , being nonnegative, and
, being nonnegative, and  such that
such that  for some
for some  , for any initial conditions in some small neighbourhood of the equilibrium, such that
, for any initial conditions in some small neighbourhood of the equilibrium, such that

which leads to

Any equilibrium point also satisfies the following constraints from (5.1)–(5.4), and (1.3) after performing the replacements  (for the initial time instant),
(for the initial time instant),  for the final time instant, for any given
for the final time instant, for any given  , and taking limits as
, and taking limits as  ,
,  ,
,  ,
,  ,
,  , and
, and  . This leads to the following implicit relations being independent of
. This leads to the following implicit relations being independent of  and being applicable for any (disease-free or endemic) equilibrium point:
and being applicable for any (disease-free or endemic) equilibrium point:

Equation (1.2) yields


Equation (1.4) yields

which is identical to (2.5), that is, either  or
or  . Equation (1.5) yields
. Equation (1.5) yields

which is identical to (2.6).
Remark 5.3.
Some fast observations useful for the model interpretation follow by simple inspection of (5.1)–(5.4) and (5.10).
-
(1)
If
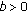 or
or  , then
, then 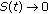 as
as 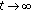 is impossible.
is impossible. -
(2)
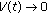 as
as 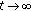 occurs if
occurs if 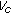 is eventually a function of time, rather than a real constant, subject to
is eventually a function of time, rather than a real constant, subject to  for some
for some 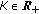 , for almost all
, for almost all  except possibly at a set of zero measure in the case that the total population does not extinguish.
except possibly at a set of zero measure in the case that the total population does not extinguish. -
(3)
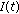 can converge to zero exponentially with time, for instance, to the disease-free equilibrium point, while being a function of exponential order
can converge to zero exponentially with time, for instance, to the disease-free equilibrium point, while being a function of exponential order  and, in such a case,
and, in such a case,  also converges to zero exponentially while being of exponential order
also converges to zero exponentially while being of exponential order 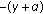 and satisfying
and satisfying  from (1.3).
from (1.3). -
(4)
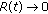 as
as  requires from (5.4) the two above corresponding conditions for the infective and vaccinated populations to converge to zero. In such a case, the convergence of the recovered population to zero is also at an exponential rate. An alternative condition for a convergence to zero of the recovered population, perhaps at a rate slower than exponential, is the convergence to zero of the function
requires from (5.4) the two above corresponding conditions for the infective and vaccinated populations to converge to zero. In such a case, the convergence of the recovered population to zero is also at an exponential rate. An alternative condition for a convergence to zero of the recovered population, perhaps at a rate slower than exponential, is the convergence to zero of the function (5.13)
(5.13)(see (5.4) with alternating sign on any two consecutive appropriate time intervals of finite lengths).
5.1. Incorporation of Impulsive Vaccination to the SVEIRS Model
Impulsive vaccination involving culling-type or removal actions on the susceptible population has being investigated recently in [18, 19]. It has also being investigated in [20] in the context of a very general SEIR model. Assume that the differential system (1.1)–(1.5) is used for modelling in open real  intervals for some given real sequence of time intervals
intervals for some given real sequence of time intervals  with
with  , for all
, for all  and an impulsive vaccination is used at time instants
and an impulsive vaccination is used at time instants  ,
,  in the sequence
in the sequence  which leads to a susceptible culling (or partial removal of susceptible from the habitat) and corresponding vaccinated increase as follows for some given real sequence
which leads to a susceptible culling (or partial removal of susceptible from the habitat) and corresponding vaccinated increase as follows for some given real sequence  , where
, where  :
:

so that  . The following simple result follows trivially.
. The following simple result follows trivially.
Theorem 5.4.
Let  and
and  be arbitrary except that the second one has all its elements in
be arbitrary except that the second one has all its elements in  for some
for some  . Then, there is no nonzero equilibrium point of the impulsive SVEIRS model (1.1)–(1.5), (5.14). If
. Then, there is no nonzero equilibrium point of the impulsive SVEIRS model (1.1)–(1.5), (5.14). If  as
as  , then the equilibrium points of the impulsive model are the same as those of the SVEIRS model (1.1)–(1.5).
, then the equilibrium points of the impulsive model are the same as those of the SVEIRS model (1.1)–(1.5).
Equations (5.1), (5.2) yield to the following recursive expressions:




The solutions in-between two consecutive impulsive vaccinations are obtained by slightly modifying (5.15)–(5.18) by replacing  by zero and
by zero and  by
by  for
for  . The following result about the oscillatory behaviour of the vaccinated population holds.
. The following result about the oscillatory behaviour of the vaccinated population holds.
Theorem 5.5.
Assume that  is a piecewise continuous function rather than a constant one with eventual bounded step discontinuities at the sequence of impulsive time instants. Define real sequences at impulsive time instants with general terms
is a piecewise continuous function rather than a constant one with eventual bounded step discontinuities at the sequence of impulsive time instants. Define real sequences at impulsive time instants with general terms

Then, the vaccinated population is an oscillating function if there is a culling sequence  of time instants for some given real sequence
of time instants for some given real sequence  with
with  , of impulsive gains if any two consecutive impulsive time instants satisfy some of the two conditions below.
, of impulsive gains if any two consecutive impulsive time instants satisfy some of the two conditions below.
Condition 1.
 and
and  with a regular piecewise continuous vaccination
with a regular piecewise continuous vaccination  and
and  .
.
Condition 2.
 and
and  with a regular piecewise continuous vaccination
with a regular piecewise continuous vaccination  and
and  .
.
Proof.
One gets directly by using lower and upper-bounds in (5.18) via  and
and  for
for 

so that as  and also for some sufficiently large
and also for some sufficiently large  ,
,

if  , and
, and

if  . Thus,
. Thus,  and
and  imply that
imply that  and
and  , and
, and  and
and  imply that
imply that  and
and  for some
for some  and some sufficiently large intervals in-between consecutive impulses
and some sufficiently large intervals in-between consecutive impulses  and
and  via the use of an admissible regular piecewise continuous vaccination
via the use of an admissible regular piecewise continuous vaccination  and
and  .
.
It turns out that Theorem 5.5 might be generalized by grouping a set of consecutive impulsive time instants such that  and
and  for some positive integers
for some positive integers  ,
,  .
.
A further property now described is that of the impulsive-free infection permanence in the sense that for sufficiently large initial conditions of the infected populations the infected population exceeds a, initial conditions dependent, positive lower-bound for all time if no impulsive vaccination is injected under any regular vaccination.
Theorem 5.6.
Assume that the SVEIRS model is positive (in the sense that no partial population reaches a negative value for any time under nonnegative initial conditions) and, furthermore, that the susceptible and vaccinated populations remain positive for all time. Assume also that the disease transmission constant is subject to the subsequent constraint

for some positive real constants dependent on the delay 

Then, the infection is permanent for all time if it strictly exceeds zero along the initialization interval.
Proof.
Note from the solution trajectories of the susceptible and vaccinated populations (5.1) and (5.2) that for some  and
and  for some real constants
for some real constants  and
and  , if
, if  and
and  . Then,
. Then,

so that, from (5.3a), since the SVEIR model is positive

The two last inequalities following from the fact that the former one stands, for all  (an "ad-hoc" complete induction reasoning will lead to an identical conclusion), and, furthermore,
(an "ad-hoc" complete induction reasoning will lead to an identical conclusion), and, furthermore,

Thus, the infection is permanent for all time if it is permanent for the initialization time interval  .
.
It is also obvious the following simplification of Theorem 5.6.
Theorem 5.7.
Theorem 5.6 still holds under (5.24) and the "ad-hoc" modified inequality (5.23) if either the susceptible or the vaccinated (but not both) population reaches zero in finite time or tends to zero asymptotically.
Proof.
It is similar to that of Theorem 5.6 by zeroing either  and
and  and removing the inverses from the corresponding conditions and proofs.
and removing the inverses from the corresponding conditions and proofs.
Close to the above results is the asymptotic permanence of the infection under sufficiently large disease constant.
Theorem 5.8.
The infection is asymptotically permanent for a positive initialization of the infected population on its initialization interval if the disease transmission constant is large enough.
Proof.
Note from (5.26) that for any given small  , there is a sufficiently large finite
, there is a sufficiently large finite  such that for any
such that for any  and any
and any  , one gets
, one gets

if the disease transmission constant is large enough to satisfy

If either  or
or  (but not both) is zero, then its inverse is removed from the above condition.
(but not both) is zero, then its inverse is removed from the above condition.
The above results suggest that the infection removal require periodic culling (or partial removal) of the susceptible population through impulsive vaccination so that both populations can become extinguished according to (5.8).
6. Simulation Results
This section contains some simulation examples illustrating the theoretical results introduced in Sections 2 and 5 concerning the existence and location of disease-free and endemic equilibrium points under regular and impulsive vaccination as well as the eventual oscillatory behavior. The objective of these examples is to numerically verify the theoretical expressions obtained there. The parameters of the model are:  (days)-1,
(days)-1,  (days)-1,
(days)-1,  days,
days,  (days)-1,
(days)-1,  ,
,  days,
days,  ,
,  (days)-1, and
(days)-1, and  days. The initial conditions are
days. The initial conditions are  ,
,  ,
,  ,
,  , and
, and  . Firstly, the disease-free case is considered in Section 6.1 while the endemic case will be treated in Sections 6.2 and 6.3.
. Firstly, the disease-free case is considered in Section 6.1 while the endemic case will be treated in Sections 6.2 and 6.3.
6.1. Disease-Free Equilibrium Point
Consider now  (days)-1,
(days)-1,  (days)-1 satisfying
(days)-1 satisfying  . The two particular cases corresponding to
. The two particular cases corresponding to  and
and  in Section 2 will be studied separately. Thus, the following simulations have been obtained for the SVEIR system (1.1)–(1.5) and
in Section 2 will be studied separately. Thus, the following simulations have been obtained for the SVEIR system (1.1)–(1.5) and  .
.
As it can be appreciated in Figure 1, the vaccinated, exposed, infected, and removed-by-immunity (or "immune" or "recovered") population converge to zero and cannot be distinguished in the figure. This situation corresponds to the case when the disease naturally vanishes. On the other hand, the susceptible population presents a different dynamics, reaching a maximum and then converging to a nonzero endemic equilibrium point. Figure 2 shows a zoom on the equilibrium point reached by the model in Figure 1.
It can be noted that the vaccinated, exposed, infectious, and removed populations are zero while the susceptible one converges to a number of 20 individuals. Furthermore, those values correspond to the ones stated in Theorem 2.1 for  , since all the populations vanish except the susceptible which converges to
, since all the populations vanish except the susceptible which converges to  . If
. If  , then the solution trajectories converge to the equilibrium point as depicted in Figure 3.
, then the solution trajectories converge to the equilibrium point as depicted in Figure 3.
In this case, only the exposed and infected tend to zero while the remaining populations tend to the values calculated in Theorem 2.1 when 

In the next example, the existence of an endemic equilibrium point is studied through a numerical simulation.
6.2. Endemic Equilibrium Point
In order to study the endemic equilibrium point, the value of  is changed now to a new value
is changed now to a new value  (days)-1 and
(days)-1 and  (days)-1 satisfying the condition
(days)-1 satisfying the condition  stated in Theorem 3.1(i) for
stated in Theorem 3.1(i) for  . Thus, the system's trajectories are showed in Figure 4.
. Thus, the system's trajectories are showed in Figure 4.
A zoom on Figure 4 will show the equilibrium point of the system as represented in Figure 5.
Figure 5 reveals that there is an endemic equilibrium point, associated to nonzero populations of the exposed and infectious, whose coordinates in view of (5.5) in Section 5 satisfy the constraints

As it can be verified in Figure 5, all the calculated values correspond to the ones obtained in the simulation example. Note that an endemic equilibrium point exists since the exposed and infected are different from zero. The endemic equilibrium point is lost when impulsive vaccination is applied on the system as the next section illustrates.
6.3. Effect of the Impulsive Vaccination on the Endemic Equilibrium Point
In this last simulation, the impulsive vaccination considered in Section 5 is introduced in the system. Thus, Equations (5.8) and (5.9) are used, at certain time instants, to remove population from susceptible while increasing the vaccinated. The impulsive vaccination is used once a week (i.e., every 7 days) with  . The following Figures 6 and 7 show the effect of the impulsive vaccination on the population of susceptible and vaccinated while Figures 8, 9, and 10 show the effect of impulses on the exposed, infected, and immune, respectively. Notice that the evolution of infected, exposed, and immune is continuous since the impulsive vaccination does not influence directly those populations.
. The following Figures 6 and 7 show the effect of the impulsive vaccination on the population of susceptible and vaccinated while Figures 8, 9, and 10 show the effect of impulses on the exposed, infected, and immune, respectively. Notice that the evolution of infected, exposed, and immune is continuous since the impulsive vaccination does not influence directly those populations.
It can be appreciated in Figure 6 that, as expected, the impulsive vaccination reduces the susceptible population in a 20%, that is, such a population is reduced drastically during the first applications of the impulse. On the other hand, Figure 7 depicts the steady-state behavior of the susceptible and vaccinated. In agreement with Theorems 5.4 and 5.5 in Section 5, the endemic equilibrium point is now lost while an oscillatory (periodic indeed) steady-state behavior is obtained. Figures 8, 9, and 10 show the effect of impulse vaccination on the exposed, infected, and immune populations, respectively. It can be observed that the impulse vaccination reduces the maximum peak of the exposed and infected populations while increases the maximum peak of the immune population. However, the solution trajectory solutions are very similar to the nonimpulsive case after the transient. The main reason for this feature relies on the fact that the susceptible population tends to a very small value during the transient and, afterwards, the influence of its variations on the exposed, susceptible, and immune populations is less relevant. Hence, the improvement on the epidemic model state-trajectory solution is concentrated on the transient. In this way, the theoretical results of the manuscript have been illustrated through simulation examples.
References
De la Sen M, Alonso-Quesada S: A control theory point of view on Beverton-Holt equation in population dynamics and some of its generalizations. Applied Mathematics and Computation 2008,199(2):464-481. 10.1016/j.amc.2007.10.021
De la Sen M, Alonso-Quesada S: Control issues for the Beverton-Holt equation in ecology by locally monitoring the environment carrying capacity: non-adaptive and adaptive cases. Applied Mathematics and Computation 2009,215(7):2616-2633. 10.1016/j.amc.2009.09.003
De la Sen M, Alonso-Quesada S: Model-matching-based control of the Beverton-Holt equation in ecology. Discrete Dynamics in Nature and Society 2008, 2008:-21.
De la Sen M: About the properties of a modified generalized Beverton-Holt equation in ecology models. Discrete Dynamics in Nature and Society 2008, 2008:-23.
De la Sen M: The generalized Beverton-Holt equation and the control of populations. Applied Mathematical Modelling 2008,32(11):2312-2328. 10.1016/j.apm.2007.09.007
Mollison D (Ed): Epidemic Models: Their Structure and Relation to Data. Publications of the Newton Institute, Cambridge University Press, Cambridge, UK; 1995. transferred to digital printing 2003
Keeling MJ, Rohani P: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton, NJ, USA; 2008:xvi+368.
Yildirim A, Cherruault Y: Analytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method. Kybernetes 2009,38(9):1566-1575. 10.1108/03684920910991540
Erturk VS, Momani S: Solutions to the problem of prey and predator and the epidemic model via differential transform method. Kybernetes 2008,37(8):1180-1188. 10.1108/03684920810884973
Ortega N, Barros LC, Massad E: Fuzzy gradual rules in epidemiology. Kybernetes 2003,32(3-4):460-477.
Khan H, Mohapatra RN, Vajravelu K, Liao SJ: The explicit series solution of SIR and SIS epidemic models. Applied Mathematics and Computation 2009,215(2):653-669. 10.1016/j.amc.2009.05.051
Song X, Jiang Y, Wei H: Analysis of a saturation incidence SVEIRS epidemic model with pulse and two time delays. Applied Mathematics and Computation 2009,214(2):381-390. 10.1016/j.amc.2009.04.005
Zhang T, Liu J, Teng Z: Dynamic behavior for a nonautonomous SIRS epidemic model with distributed delays. Applied Mathematics and Computation 2009,214(2):624-631. 10.1016/j.amc.2009.04.029
Mukhopadhyay B, Bhattacharyya R: Existence of epidemic waves in a disease transmission model with two-habitat population. International Journal of Systems Science. Principles and Applications of Systems and Integration 2007,38(9):699-707.
Barreiro A, Baños A: Delay-dependent stability of reset systems. Automatica 2010,46(1):216-221. 10.1016/j.automatica.2009.10.029
De la Sen M: On positivity of singular regular linear time-delay time-invariant systems subject to multiple internal and external incommensurate point delays. Applied Mathematics and Computation 2007,190(1):382-401. 10.1016/j.amc.2007.01.053
de la Sen M: Quadratic stability and stabilization of switched dynamic systems with uncommensurate internal point delays. Applied Mathematics and Computation 2007,185(1):508-526. 10.1016/j.amc.2006.07.048
Jiang Y, Wei H, Song X, Mei L, Su G, Qiu S: Global attractivity and permanence of a delayed SVEIR epidemic model with pulse vaccination and saturation incidence. Applied Mathematics and Computation 2009,213(2):312-321. 10.1016/j.amc.2009.03.024
Song X, Jiang Y, Wei H: Analysis of a saturation incidence SVEIRS epidemic model with pulse and two time delays. Applied Mathematics and Computation 2009,214(2):381-390. 10.1016/j.amc.2009.04.005
De la Sen M, Agarwal RP, Ibeas A, Alonso-Quesada S: On a generalized time-varying SEIR epidemic model with mixed point and distributed time-varying delays and combined regular and impulsive vaccination controls. Advances in Difference Equations 2010., 2010:
Wei H, Jiang Y, Song X, Su GH, Qiu SZ: Global attractivity and permanence of a SVEIR epidemic model with pulse vaccination and time delay. Journal of Computational and Applied Mathematics 2009,229(1):302-312. 10.1016/j.cam.2008.10.046
Kaddar A: Stability analysis in a delayed SIR epidemic model with a saturated incidence rate. Nonlinear Analysis: Modelling and Control 2010,15(3):299-306.
Acknowledgments
The authors thank the Spanish Ministry of Education for the Grant no. DPI2009-07197. They are also grateful to the Basque Government by its support through Grants nos. IT378-10, SAIOTEK S-PE08UN15, and SAIOTEK SPE07UN04 and SPE09UN12. The authors are also grateful to the reviewers for their suggestions to improve the former version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M., Agarwal, R.P., Ibeas, A. et al. On the Existence of Equilibrium Points, Boundedness, Oscillating Behavior and Positivity of a SVEIRS Epidemic Model under Constant and Impulsive Vaccination. Adv Differ Equ 2011, 748608 (2011). https://doi.org/10.1155/2011/748608
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/748608
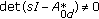 , for all
, for all  , equivalently,
, equivalently, 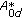 is a stability matrix
is a stability matrix -matrix measure
-matrix measure  of
of 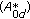 is negative, and, furthermore, the following constraint holds
is negative, and, furthermore, the following constraint holds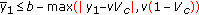

 for
for  and
and  for
for 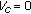 . Thus, there is at least one endemic equilibrium point at which the susceptible, vaccinated, infected, exposed, and recovered populations are positive and the vaccinated population is zero if and only if
. Thus, there is at least one endemic equilibrium point at which the susceptible, vaccinated, infected, exposed, and recovered populations are positive and the vaccinated population is zero if and only if 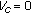 (i.e., in the absence of vaccination action). Furthermore, such an equilibrium point satisfies the constraints
(i.e., in the absence of vaccination action). Furthermore, such an equilibrium point satisfies the constraints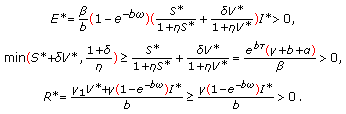
 for
for 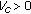 , and
, and  for
for 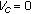 , then there is no reachable endemic equilibrium point.
, then there is no reachable endemic equilibrium point.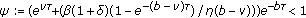 , then the total population is uniformly bounded for all time, irrespective of the susceptible and vaccinated populations, for any bounded initial conditions and
, then the total population is uniformly bounded for all time, irrespective of the susceptible and vaccinated populations, for any bounded initial conditions and
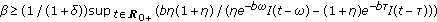 subject to
subject to  and
and 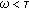 , then
, then 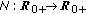 is monotone decreasing and of negative exponential order so that the total population exponentially extinguishes as a result.
is monotone decreasing and of negative exponential order so that the total population exponentially extinguishes as a result.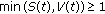 (equivalently if
(equivalently if  ), then
), then 
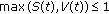 (equivalently, if
(equivalently, if  , then
, then 
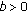 or
or  , then
, then 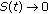 as
as 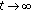 is impossible.
is impossible.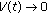 as
as 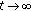 occurs if
occurs if 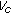 is eventually a function of time, rather than a real constant, subject to
is eventually a function of time, rather than a real constant, subject to  for some
for some 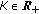 , for almost all
, for almost all  except possibly at a set of zero measure in the case that the total population does not extinguish.
except possibly at a set of zero measure in the case that the total population does not extinguish.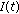 can converge to zero exponentially with time, for instance, to the disease-free equilibrium point, while being a function of exponential order
can converge to zero exponentially with time, for instance, to the disease-free equilibrium point, while being a function of exponential order  and, in such a case,
and, in such a case,  also converges to zero exponentially while being of exponential order
also converges to zero exponentially while being of exponential order 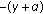 and satisfying
and satisfying  from (1.3).
from (1.3).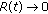 as
as  requires from (5.4) the two above corresponding conditions for the infective and vaccinated populations to converge to zero. In such a case, the convergence of the recovered population to zero is also at an exponential rate. An alternative condition for a convergence to zero of the recovered population, perhaps at a rate slower than exponential, is the convergence to zero of the function
requires from (5.4) the two above corresponding conditions for the infective and vaccinated populations to converge to zero. In such a case, the convergence of the recovered population to zero is also at an exponential rate. An alternative condition for a convergence to zero of the recovered population, perhaps at a rate slower than exponential, is the convergence to zero of the function

 .
.
 .
.
 .
.





