- Research Article
- Open access
- Published:
Annular Bounds for Polynomial Zeros and Schur Stability of Difference Equations
Advances in Difference Equations volume 2011, Article number: 782057 (2011)
Abstract
We investigate the monic complex-coefficient polynomial of degree  in the complex variable
in the complex variable  and obtain a new annular bound for the zeros of
and obtain a new annular bound for the zeros of  , which is sharper than the previous results and has clear advantages in judging the Schur stability of difference equations. In addition, examples are given to illustrate the theoretical result.
, which is sharper than the previous results and has clear advantages in judging the Schur stability of difference equations. In addition, examples are given to illustrate the theoretical result.
1. Introduction
It is well known that many discrete-time systems in engineering are described in terms of a difference equation, and the characteristic equation for the difference equation plays a key role in the study of the behaviors of the solutions, especially the stability of the solutions, to the discrete-time systems. Since the characteristic equations for difference equations are closely related to some complex polynomials, the estimates of the bound for the moduli of various complex polynomial zeros have been investigated by many researchers (cf. e.g., [1–8] and references therein). In the study on this issue, one of meaningful research ideas is to indicate such a common property of a lot of polynomials by a few very special polynomials. Using this idea, a good annular bound by estimating the largest nonnegative zeros of four specific polynomials is given in [8] recently. As a continuation of this work and our paper [4], in this paper we investigate further the location of the zeros of complex-coefficient polynomials on the basis of such a research idea and establish a new annular bound theorem (Theorem 3.1), which improves the previous corresponding result and has clear advantages in judging the Schur stability of difference equations. Examples are given to illustrate the advantages of the new result.
2. Preliminaries
Throughout this paper, we let

with  ,
,  , and
, and

Without losing the generality, we assume that  , or, equivalently,
, or, equivalently,  .
.
Basic notations are as follows.
: ,
,
: the modulus of a complex number  ,
,
: the set of all zeros of  ,
,
: with
with  ,
,
: the smallest positive integer such that  in
in  ,
,
: the largest positive integer such that  in
in  ,
,
: the smallest positive integer such that  in
in  ,
,
: the largest positive integer such that  in
in  ,
,
: the integer part of a real number  .
.
In order to simplify the expressions in our study, we define specially that

for any positive integers  ,
, 
 , and sequence
, and sequence  . This notation is logical and useful in the note.
. This notation is logical and useful in the note.
Moreover, we write

with  and
and  ,
,

with  ,
,

with  and
and  ,
,

with  ,
,

Remark 2.1.
By Descartes' rule of signs, it is easy to see that for each  , the polynomial
, the polynomial 
 ,
,  ,
,  has a unique positive zero.
has a unique positive zero.
We denote by  ,
,  ,
,  , and
, and  the unique positive zero of
the unique positive zero of  ,
,  ,
,  , and
, and  , respectively.
, respectively.
3. Main Result
The following result is established in [8].
Theorem A (see [8]).
 ,
,  and
and  .
.
Theorem 3.1.
Let  ,
,  , and
, and  ,
,  . Then
. Then
-
(i)
 (3.1)
(3.1)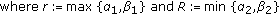
-
(ii)
 (3.2)
(3.2)where
 ,
,  are constants as in Theorem A;
are constants as in Theorem A; -
(iii)
the annular bound of original polynomial
 can be further improved by iterative procedure.
can be further improved by iterative procedure.
Proof.
Define



where  . Then it is not difficult to see that
. Then it is not difficult to see that

This implies that for every  we have
we have

that is,

Hence, by (3.8), one has

which imply that

In addition, it follows from (2.4)–(2.7) that

Therefore, for each  we have
we have

which imply that (3.1) is hold. So (i) is proved.
Next we prove that (ii) holds. Actually, we have

where  and
and  .
.
On the other hand, since the polynomial equation  has a unique positive root
has a unique positive root  and
and

we get  by combining(3.13) and (3.14).
by combining(3.13) and (3.14).
In addition, we have

Since

we have  .
.
In the same way, we can obtain  and
and  ; therefore,
; therefore,

Finally, we prove (iii). Set

with

and let  be the smallest positive integer such that
be the smallest positive integer such that  in
in  . If
. If  , in analogy to (3.3) and (2.4), we can define
, in analogy to (3.3) and (2.4), we can define

and  , respectively. It is not difficult to see that, the unique positive root of polynomial
, respectively. It is not difficult to see that, the unique positive root of polynomial  ,
,  . Similarly, we can define
. Similarly, we can define  ,
,  , and
, and  , respectively. Moreover, their respective positive roots
, respectively. Moreover, their respective positive roots  ,
,  , and
, and  satisfy that
satisfy that

Consequently, new annular bound of  , namely,
, namely,  with
with

is better than (3.1). This procedure can be applied iteratively.

can be further transformed into

respectively, and

into

until the last iteration brings no practical improvement. Obviously, when  increases,
increases,

will approach the smallest and largest modulus of polynomial zero, respectively, where

denotes the unique positive root of

This means that (iii) is true.
Remark 3.2.
-
(a)
When
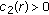 , it follows from (3.14) and (3.15) that for every
, it follows from (3.14) and (3.15) that for every  ,
, 
 , that is,
, that is, 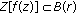 , that is,
, that is,  is
is  -stable. Similarly, we can draw the same conclusion when
-stable. Similarly, we can draw the same conclusion when 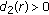 , and
, and 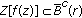 when
when  or
or 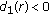 .(b) By the similar arguments in the proof of (iii) of Theorem 3.1, the results in (a) can be improved. This also provides an iterative algorithm to test the r-stability and Schur stability of polynomials. (c) The question "What happens to Theorem 3.1 when
.(b) By the similar arguments in the proof of (iii) of Theorem 3.1, the results in (a) can be improved. This also provides an iterative algorithm to test the r-stability and Schur stability of polynomials. (c) The question "What happens to Theorem 3.1 when  ,
, 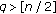 , and
, and 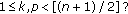 " is worth considering further.
" is worth considering further.
Example 3.3.
Let

where  . By Theorem 3.1, we obtain
. By Theorem 3.1, we obtain

If we start the iterative procedure given in the proof of (iii) of Theorem 3.1, after five iterations, we obtain

On the other hand, by Theorem A, one only can have

The following examples show the advantages of Theorems 3.1 over Theorem A in analyzing the Schur stability of difference equations (discrete-time systems).
Example 3.4.
Let the characteristic polynomial of a difference equation (discrete-time system) be given by

where  . Then by Theorem 3.1, we get
. Then by Theorem 3.1, we get  , which implies that all zeros of
, which implies that all zeros of  lie in the open unit disk, that is, this system is Schur stable. However, by Theorem A, one has
lie in the open unit disk, that is, this system is Schur stable. However, by Theorem A, one has

So Theorem A cannot guarantee the stability of such a system.
Example 3.5.
Suppose the characteristic polynomial of a difference equation (discrete-time system) is given by

where  . Then by Theorem 3.1, we have
. Then by Theorem 3.1, we have  , which implies that all zeros of
, which implies that all zeros of  are outside the open unit disk, namely, such a system is instable. By Theorem A, one has
are outside the open unit disk, namely, such a system is instable. By Theorem A, one has

which cannot determine the instability of this system.
Example 3.6.
Consider the following characteristic polynomial of a difference equation (discrete-time system):

In this example,

Consequently, such a difference equation (discrete-time system) is Schur stable.
References
Boese FG, Luther WJ: A note on a classical bound for the moduli of all zeros of a polynomial. IEEE Transactions on Automatic Control 1989,34(9):998-1001. 10.1109/9.35817
Cargo GT, Shisha O: Zeros of polynomials and fractional order differences of their coefficients. Journal of Mathematical Analysis and Applications 1963, 7: 176-182. 10.1016/0022-247X(63)90046-5
Gardner RB, Govil NK: On the location of the zeros of a polynomial. Journal of Approximation Theory 1994,78(2):286-292. 10.1006/jath.1994.1078
Liang J, Li K: A new stability criterion for polynomials with the quasi-critical condition. International Journal of Nonlinear Sciences and Numerical Simulation 2008,9(3):289-292. 10.1515/IJNSNS.2008.9.3.289
Marden M: Geometry of Polynomials, Mathematical Surveys, No. 3. 2nd edition. American Mathematical Society, Providence, RI, USA; 1966:xiii+243.
Milovanovic GV, Milovanovic DS, Rassias TM: Topics in Polynomials, Extremal Problems, Inequalities, Zeros. World Scientic, Singapore; 1994.
Rahman QI, Schmeisser G: Analytic Theory of Polynomials. Oxford University Press, Oxford, UK; 2005:xiv+742.
Sun Y-J: New result for the annular bounds of complex-coefficient polynomial zeros. IEEE Transactions on Automatic Control 2004,49(5):813-814. 10.1109/TAC.2004.828323
Acknowledgments
This work was supported partially by the NSF of China (10771202) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2007035805).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, K., Liang, J. Annular Bounds for Polynomial Zeros and Schur Stability of Difference Equations. Adv Differ Equ 2011, 782057 (2011). https://doi.org/10.1155/2011/782057
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/782057

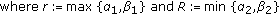

 ,
,  are constants as in Theorem A;
are constants as in Theorem A; can be further improved by iterative procedure.
can be further improved by iterative procedure.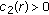 , it follows from (3.14) and (3.15) that for every
, it follows from (3.14) and (3.15) that for every  ,
, 
 , that is,
, that is, 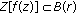 , that is,
, that is,  is
is  -stable. Similarly, we can draw the same conclusion when
-stable. Similarly, we can draw the same conclusion when 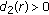 , and
, and 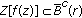 when
when  or
or 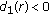 .(b) By the similar arguments in the proof of (iii) of Theorem 3.1, the results in (a) can be improved. This also provides an iterative algorithm to test the r-stability and Schur stability of polynomials. (c) The question "What happens to Theorem 3.1 when
.(b) By the similar arguments in the proof of (iii) of Theorem 3.1, the results in (a) can be improved. This also provides an iterative algorithm to test the r-stability and Schur stability of polynomials. (c) The question "What happens to Theorem 3.1 when  ,
, 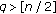 , and
, and 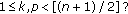 " is worth considering further.
" is worth considering further.