- Research Article
- Open access
- Published:
Multiple Periodic Solutions for Difference Equations with Double Resonance at Infinity
Advances in Difference Equations volume 2011, Article number: 806458 (2011)
Abstract
By using variational methods and Morse theory, we study the multiplicity of the periodic solutions for a class of difference equations with double resonance at infinity. To the best of our knowledge, investigations on double-resonant difference systems have not been seen in the literature.
1. Introduction
Denote by  the set of integers. For a given positive integer
the set of integers. For a given positive integer  , consider the following periodic problem on difference equation:
, consider the following periodic problem on difference equation:

where  is the forward difference operator defined by
is the forward difference operator defined by  and
and  for
for  . In this paper, we always assume that
. In this paper, we always assume that
(f1) is
is  -differentiable with respect to the second variable and satisfies
-differentiable with respect to the second variable and satisfies  for
for  and
and  for
for  .
.
As a natural phenomenon, resonance may take place in the real world such as machinery, construction, electrical engineering, and communication. In a system described by a mathematical model, the feature of resonance lies in the interaction between the linear spectrum and the nonlinearity. It is known (see [1]) that the eigenvalue problem

possess  distinct eigenvalues
distinct eigenvalues  , where
, where  , that is, the integer part of
, that is, the integer part of  .
.
For  with
with  , define
, define  . Now, we suppose that
. Now, we suppose that
(f2) , and there exists some
, and there exists some  such that
such that

Remark 1.1.
The assumption (f2) characterizes problem (1.1) as double resonant between two consecutive eigenvalues at infinity. Problem (1.1) is the discrete analogue of the differential equation with double resonance

whose solvability has been studied in [2], where  is a differentiable function satisfying
is a differentiable function satisfying

for some  and uniformly for a.e.
and uniformly for a.e.  .
.
Recently, many authors have studied the boundary value problems on nonlinear differential equations with double resonance(see [2–5]). It is well known that in different fields of research, such as computer science, mechanical engineering, control systems, artificial or biological neural networks, and economics, the mathematical modelling of important questions leads naturally to the consideration of nonlinear difference equations. For this reason, in recent years the solvability of nonlinear difference equations have been extensively investigated(see [1, 6–8] and the references cited therein). However, to the best of our knowledge, investigations on double resonant difference systems have not been seen in the literature.
In this paper, several theorems on the multiplicity of the periodic solutions to the double resonant system (1.1) are obtained via variational methods and Morse theory. The research here was mainly motivated by the works [2, 4].
We need the following assumptions  and
and  :
:
 , and there exists some
, and there exists some  such that
such that

(f4±)for some  ,
,

Remark 1.2.
The assumption  implies
implies  and will be employed to control the resonance at infinity. We will need
and will be employed to control the resonance at infinity. We will need  in the case that (1.1) is also resonant at the origin.
in the case that (1.1) is also resonant at the origin.
Now, the main results of this paper are stated as follows.
Theorem 1.3.
Assume that (f1) and (f3) hold. Then, problem (1.1) has at least two nontrivial  -periodic solutions in each of the following two cases:
-periodic solutions in each of the following two cases:
-
(i)
 and
and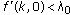 for
for  ,
, -
(ii)
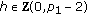 and
and for
for 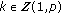 .
.
Theorem 1.4.
Assume that (f1) and (f3) hold. If there exists  with
with  such that
such that  , then problem (1.1) has at least two nontrivial
, then problem (1.1) has at least two nontrivial  -periodic solutions.
-periodic solutions.
Theorem 1.5.
Assume that (f1) and (f3) hold. If there exists  such that
such that  for
for  . Then problem (1.1) has at least two nontrivial
. Then problem (1.1) has at least two nontrivial  -periodic solutions in each of the following two cases:
-periodic solutions in each of the following two cases:
-
(i)
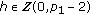 and
and with
with 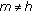 ,
, -
(ii)
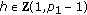 and
and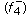 with
with 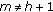 .
.
In Section 3, we will prove the main results, before which some preliminary results on Morse theory will be collected in Section 2. Some fundamental facts relative to (1.1) revealed here will benefit the further investigations in this direction, which will be remarked in Section 4.
2. Preliminary Results on Critical Groups
In this section, we recall some basic facts in Morse theory which will be used in the proof of the main results. For the systematic discussion on Morse theory, we refer the reader to the monograph [9] and the references cited therein. Let  be a Hilbert space and
be a Hilbert space and  be a functional satisfying the compactness condition (PS), that is, every sequence
be a functional satisfying the compactness condition (PS), that is, every sequence  such that
such that  is bounded and that
is bounded and that  as
as  contains a convergent subsequence. Denote by
contains a convergent subsequence. Denote by  the
the  th singular relative homology group of the topological pair
th singular relative homology group of the topological pair  with integer coefficients. Let
with integer coefficients. Let  be an isolated critical point of
be an isolated critical point of  with
with  ,
,  , and
, and  be a neighborhood of
be a neighborhood of  . For
. For  , the group
, the group

is called the  th critical group of
th critical group of  at
at  , where
, where  .
.
If the set of critical points of  , denoted by
, denoted by  , is finite and
, is finite and  , the critical groups of
, the critical groups of  at infinity are defined by (see [10])
at infinity are defined by (see [10])

For  , we call
, we call  the Betti numbers of
the Betti numbers of  and define the Morse-type numbers of the pair
and define the Morse-type numbers of the pair  by
by

The following facts  are derived from [6, Chapter 8].
are derived from [6, Chapter 8].
(2.a)If  for some
for some  , then there exists
, then there exists  such that
such that  ,
,
(2.b)If  , then
, then  ,
,
(2.c) ,
,
(2.d) .
.
If  and
and  is a Fredholm operator and the Morse index
is a Fredholm operator and the Morse index  and nullity
and nullity  of
of  are finite, then we have
are finite, then we have
(2.e) for
for  ,
,
(2.f)If  then
then  and if
and if  then
then  ,
,
(2.g) If  , then
, then  when
when  is local minimum of
is local minimum of  , while
, while  when
when  is the local maximum of
is the local maximum of  .
.
We say that  has a local linking at
has a local linking at  if there exist the direct sum decompositions
if there exist the direct sum decompositions  and
and  such that
such that

The following results were due to Su [5].
(2.h)Assume that  has a local linking at
has a local linking at  with respect to
with respect to  and
and  . Then,
. Then,

3. Proofs of Main Results
In this section, we will establish the variational structure relative to problem (1.1) and prove the main results via Morse theory.
Denote  and
and

Equipped with the inner product  and norm
and norm  as follows:
as follows:

 is linearly homeomorphic to
is linearly homeomorphic to  . Throughout this paper, we always identify
. Throughout this paper, we always identify  with
with  .
.
Define the operator  by
by  and denote
and denote  ,
,  , where
, where  is the identity operator. Set
is the identity operator. Set

then  has the decomposition
has the decomposition  . In the rest of this paper, the expression
. In the rest of this paper, the expression  for
for  always means
always means  ,
,  .
.
Remark 3.1.
From the discussion in [1, Section 2], we see that  ,
,  , for
, for  and
and  if
if  is even or
is even or  if
if  is odd.
is odd.
Define a family of functionals  ,
,  by
by

where  ,
,  . Then, the Fréchet derivative of
. Then, the Fréchet derivative of  at
at  , denoted by
, denoted by  , can be described as (see [1])
, can be described as (see [1])

where  and
and

Remark 3.2.
From (3.5) with  , we know by computation(or see [1]) that
, we know by computation(or see [1]) that  is a critical point of
is a critical point of  if and only if
if and only if  is a
is a  -periodic solution of problem (1.1). Moreover,
-periodic solution of problem (1.1). Moreover,  is
is  differentiable and
differentiable and

where  is the derivative of
is the derivative of  with respect to
with respect to  .
.
Let  ,
,  and
and  consist of
consist of  satisfying
satisfying

Remark 3.3.
 is the solution space of the system
is the solution space of the system  ,
,  , where
, where

Thus,  since
since  possesses of non-degenerate
possesses of non-degenerate  order submatrixes.
order submatrixes.
Lemma 3.4.
If  ,
,  and
and  satisfies (3.8), where
satisfies (3.8), where  and
and  , then either
, then either  or
or  .
.
Proof.
Setting  and
and  , respectively, in (3.8), we have
, respectively, in (3.8), we have

Comparing the above two equalities, we get

which, by  ,
,  , implies that
, implies that

On the other hand, by the definition of  and
and  , we have
, we have

where  . There are two cases to be considered.
. There are two cases to be considered.
Case 1.
 for
for  . Then by (3.12),
. Then by (3.12),  and
and  for
for  , that is,
, that is,  .
.
Case 2.
There exists  such that
such that  . By (3.13), we have
. By (3.13), we have

If  , then
, then  which, by (3.13), implies that
which, by (3.13), implies that  for
for  , that is,
, that is,  . If
. If  , then
, then  . This, by (3.12), implies
. This, by (3.12), implies  and
and  . Thus, by (3.13),
. Thus, by (3.13),  for
for  , that is
, that is  . The proof is complete.
. The proof is complete.
Set  and
and  . The following Lemmas 3.5–3.7 benefit from [4].
. The following Lemmas 3.5–3.7 benefit from [4].
Lemma 3.5.
Assume that (f1) and (f2) hold. Let  and
and  satisfy
satisfy  and
and 
 as
as  . Then,
. Then,

Proof.
From (f2), we have

where the limitation is uniformly in  . It follows that for any
. It follows that for any  , there exists
, there exists  such that
such that

Thus, there exists  such that
such that

By the assumption on  , we have
, we have  . It follows from (3.5) that
. It follows from (3.5) that

which, combining with (3.18), implies that

By using, Holder inequality on the above two summations, we get

which leads to

Note that  is arbitrarily small, we get (3.15), and the proof is complete.
is arbitrarily small, we get (3.15), and the proof is complete.
Lemma 3.6.
Under the conditions of Lemma 3.5, one further has

Proof.
Since  ,
,  , and
, and  are invariant with respect to
are invariant with respect to  , we have
, we have

If, for the contradiction, (3.23) is false, then there is a subsequence of  , called
, called  again, and a number
again, and a number  , such that
, such that  ,
,  . Then,
. Then,

where  .
.
By the fact that  and
and  are two consecutive eigenvalues of
are two consecutive eigenvalues of  with corresponding eigenspace
with corresponding eigenspace  and
and  , we have
, we have  and then, the function
and then, the function  is strictly decreasing on
is strictly decreasing on  with
with  as
as  . Besides,
. Besides,  . So, by (3.25),
. So, by (3.25),

This contradict to (3.15) and the proof is complete.
Lemma 3.7.
Under the assumption of Lemma 3.5, there exists a subsequence of  , still called
, still called  , such that
, such that

Proof.
Since  as
as  , we can assume (by passing to a subsequence if necessary) that
, we can assume (by passing to a subsequence if necessary) that

Thus, (3.16) implies

which implies that there exists a subsequence of  , still called
, still called  , and
, and  , such that
, such that

Let  , then
, then  , and, by Lemma 3.6, there is a convergent subsequence of
, and, by Lemma 3.6, there is a convergent subsequence of  , call it
, call it  again, such that
again, such that

To prove (3.27), we only need to show that  or
or  . For every
. For every  , we have
, we have  as
as  , that is,
, that is,

If  as
as  for
for  , then we can rewrite (3.32) as
, then we can rewrite (3.32) as

Letting  in (3.33) and using (3.30) and (3.31), we get
in (3.33) and using (3.30) and (3.31), we get

Since  for
for  , by setting
, by setting  for
for  , we rewrite (3.34) as
, we rewrite (3.34) as

Obviously, if  , (3.35) still holds. By Lemma 3.4,
, (3.35) still holds. By Lemma 3.4,  or
or  and the proof is complete.
and the proof is complete.
Lemma 3.8.
Assume that  and
and  hold. Let
hold. Let  and
and  satisfy
satisfy  and
and  as
as  . Then, there exists a subsequence of
. Then, there exists a subsequence of  , still called
, still called  , such that
, such that

Proof.
As that in the above proof, we can assume that  satisfies (3.28). Noticing that (f3) implies (f2) and by Lemma 3.7, we have two cases to be considered.
satisfies (3.28). Noticing that (f3) implies (f2) and by Lemma 3.7, we have two cases to be considered.
Case 1.
 as
as  . We have
. We have  as
as  and
and

If  , then
, then  and
and  are bounded for
are bounded for  and
and  . It follows that
. It follows that  as
as  for
for  and
and

By (f3(i)), there exist  and
and  such that
such that  and
and  for
for  and
and  . Then, for
. Then, for  ,
,  and
and  ,
,

Choose  such that
such that  for
for  and
and  . It follows that
. It follows that

where  . Since
. Since  is a finite dimensional vector space and possesses another norm defined by
is a finite dimensional vector space and possesses another norm defined by  ,
,  , which is equivalent to
, which is equivalent to  , there exists a positive constant
, there exists a positive constant  such that
such that  ,
,  . Thus, by (3.37)–(3.40),
. Thus, by (3.37)–(3.40),

Obviously, if  , the above inequality still holds.
, the above inequality still holds.
Case 2.
 as
as  . By using
. By using  , we can show that
, we can show that  in the same way. The proof is complete.
in the same way. The proof is complete.
In the rest of this section, we will use the facts ( )–(
)–( ) stated in Section 2 to complete the proofs.
) stated in Section 2 to complete the proofs.
Lemma 3.9.
Let  satisfy (f1) and (f3). Then, for every
satisfy (f1) and (f3). Then, for every  ,
,  satisfies the (PS) condition and
satisfies the (PS) condition and

Proof.
First we have the following claim:
Claim 1.
For any sequences  and
and if
if as
as , then
, then  is bounded.
is bounded.
In fact, if  is unbounded, there exists a subsequence, still called
is unbounded, there exists a subsequence, still called  , such that
, such that  as
as  . By Lemma 3.8, there exists a subsequence, still called
. By Lemma 3.8, there exists a subsequence, still called  , such that
, such that  or
or  .
.
On the other hand,  as
as , that is
, that is

Note that  ,
,  , it follows that
, it follows that  . This contradiction proves Claim 1.
. This contradiction proves Claim 1.
Setting  in Claim 1, we see that
in Claim 1, we see that  satisfies (PS) condition. Now, we start to prove (3.42). Define a functional
satisfies (PS) condition. Now, we start to prove (3.42). Define a functional  as
as

Claim 2.
There exist  such that
such that

In fact, if Claim 2 is not true, there exists  and
and  such that
such that  and
and  as
as  , which contradict Claim 1.
, which contradict Claim 1.
Noticing that  , we set
, we set  . Then,
. Then,  implies
implies  . Consider the flow
. Consider the flow  generated by
generated by

The chain rule for differentiation reads  . Thus,
. Thus,

and  ,
,  , which implies that
, which implies that  ,
,  . Then, the flow
. Then, the flow  is well defined on
is well defined on  and
and  is a homeomorphism of
is a homeomorphism of  to
to  and (see [11])
and (see [11])

On the other hand,

Note that  is the unique critical point of
is the unique critical point of  with Morse index
with Morse index  (see Remark 3.1) and nullity
(see Remark 3.1) and nullity  . Then, by (2.b), (2.f) and (3.48), we have
. Then, by (2.b), (2.f) and (3.48), we have

The proof is completed.
Proof of Theorem 1.3.
By lemma 3.9, we get (3.42) which, by  , implies that there exists
, implies that there exists  with
with

Since  , we have
, we have  . Denote by
. Denote by  and
and  the Morse index and nullity of
the Morse index and nullity of  . By
. By  , we get
, we get  .
.
Denote  . Then, from (3.7) and Remark 3.3, we see that
. Then, from (3.7) and Remark 3.3, we see that  .
.
In Case (i),  is a local minimum of
is a local minimum of  , hence, by (
, hence, by ( ),
),

which, by comparing with (3.51), implies that  . Besides,
. Besides,  since
since  . Assume, for the contradiction, that
. Assume, for the contradiction, that  is the unique nontrivial critical point of
is the unique nontrivial critical point of  , then
, then  . If
. If  or
or  , we have, by (
, we have, by ( ),
),

from which, ( ) reads
) reads  , a contradiction.
, a contradiction.
If  , then
, then  and
and  . Since
. Since  , we have
, we have  . Thus, (
. Thus, ( ) with
) with  reads
reads  , also a contradiction.
, also a contradiction.
In Case (ii),  is a local maximum of
is a local maximum of  , hence, by (
, hence, by ( ),
),

which, by comparing with (3.51), implies that  . Besides,
. Besides,  since
since  . Assume, for the contradiction, that
. Assume, for the contradiction, that  is the unique nontrivial critical point of
is the unique nontrivial critical point of  , then
, then  . If
. If  or
or  , then (3.53) holds, from which,
, then (3.53) holds, from which,  ) reads
) reads

a contradiction. If  , then
, then  and, by (
and, by ( ),
),

Note that  , we have
, we have  . Thus, (
. Thus, ( ) with
) with  and with
and with  reads
reads

respectively, which implies that  . Then, (
. Then, ( ) reads (3.55), also a contradiction. The proof is complete.
) reads (3.55), also a contradiction. The proof is complete.
Proof of Theorem 1.4.
As above, there exists  with the Morse index
with the Morse index  , and nullity
, and nullity  satisfying
satisfying  ,
,  , and (3.51) holds.
, and (3.51) holds.
On the other hand,  is a nondegenerate critical point of
is a nondegenerate critical point of  with Morse index, denoted by
with Morse index, denoted by  . Thus,
. Thus,  and
and  since
since  , which, by comparing with (3.51), implies that
, which, by comparing with (3.51), implies that  .
.
Assume for the contradiction, that  is unique nontrivial critical point of
is unique nontrivial critical point of  , then
, then  . If
. If  or
or  , then (3.53) holds and (
, then (3.53) holds and ( ) reads the contradicition
) reads the contradicition  .
.
Now, we consider the case  where we have
where we have  and
and  with (3.56). Since
with (3.56). Since  , we know that either
, we know that either  or
or  . If
. If  , (
, ( ) with
) with  reads contradiction
reads contradiction  . If
. If  , by similar argument, we can get (3.57). Thus
, by similar argument, we can get (3.57). Thus  and (
and ( ) reads the contradiction
) reads the contradiction  . The proof is complete.
. The proof is complete.
The proof of the following lemma is similar to that of ([12]) and is omitted.
Lemma 3.10.
Let  satisfy
satisfy 
 or
or  . Then
. Then  has a local linking at
has a local linking at  with respect to the decomposition
with respect to the decomposition  , where
, where  (or
(or  , respectively).
, respectively).
Proof of Theorem 1.5.
Now  . Thus,
. Thus,  is a degenerate critical point of
is a degenerate critical point of  . Let
. Let  and
and  denote the Morse index and nullity of 0. By Lemma 3.10 and (
denote the Morse index and nullity of 0. By Lemma 3.10 and ( ), we have
), we have

where  or
or  corresponding to the case (
corresponding to the case ( ) or the case (
) or the case ( ), respectively. The rest of the proof is similar and is omitted. The proof is complete.
), respectively. The rest of the proof is similar and is omitted. The proof is complete.
4. Conclusion and Future Directions
It is known that there have been many investigations on the solvability of elliptic equations with double-resonance via variational methods, where the so called unique continuation property of the Laplace operator, proved by Robinson [4], plays an important role in proving the compactness of the corresponding functional (see [2–5] and the references cited therein). In this paper, the solvability of the periodic problem on difference equations with double resonance is first studied and the "unique continuation property" of the second-order difference operator is derived by proving Lemma 3.4.
In addition, under the double resonance assumption  and
and  , some fundamental facts relative to (1.1) are revealed in Lemmas 3.5–3.7, on which, further investigations, employing new restrictions different from (f3) and (f4), may be based.
, some fundamental facts relative to (1.1) are revealed in Lemmas 3.5–3.7, on which, further investigations, employing new restrictions different from (f3) and (f4), may be based.
On the observations as above, it is reasonable to believe that the research in this paper will benefit the future study in this direction.
References
Yu J, Long Y, Guo Z: Subharmonic solutions with prescribed minimal period of a discrete forced pendulum equation. Journal of Dynamics and Differential Equations 2004,16(2):575-586. 10.1007/s10884-004-4292-2
Su J, Zhao L: Multiple periodic solutions of ordinary differential equations with double resonance. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1520-1527. 10.1016/j.na.2008.02.031
Fabry C, Fonda A: Periodic solutions of nonlinear differential equations with double resonance. Annali di Matematica Pura ed Applicata 1990, 157: 99-116. 10.1007/BF01765314
Robinson S: Double resonance in semilinear elliptic boundary value problems over bounded and unbounded domains. Nonlinear Analysis: Theory, Methods & Applications 1993,21(6):407-424. 10.1016/0362-546X(93)90125-C
Su J: Semilinear elliptic boundary value problems with double resonance between two consecutive eigenvalues. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):881-895. 10.1016/S0362-546X(00)00221-2
Guo Z, Yu J: The existence of periodic and subharmonic solutions of subquadratic second order difference equations. Journal of the London Mathematical Society 2003,68(2):419-430. 10.1112/S0024610703004563
Guo Z, Yu J: Existence of periodic and subharmonic solutions for second-order superlinear difference equations. Science in China A 2003,46(4):506-515.
Zhu B, Yu J: Multiple positive solutions for resonant difference equations. Mathematical and Computer Modelling 2009,49(9-10):1928-1936. 10.1016/j.mcm.2008.09.009
Mawhin J, Willem M: Critical Point Theory and Hamiltonian Systems, Applied Mathematical Sciences. Volume 74. Springer, New York, NY, USA; 1989:xiv+277.
Bartsch T, Li S: Critical point theory for asymptotically quadratic functionals and applications to problems with resonance. Nonlinear Analysis: Theory, Methods & Applications 1997,28(3):419-441. 10.1016/0362-546X(95)00167-T
Perera K, Schechter M: Nontrivial solutions of elliptic semilinear equations at resonance. Manuscripta Mathematica 2000,101(3):301-311. 10.1007/s002290050217
Li SJ, Liu JQ: Nontrivial critical points for asymptotically quadratic function. Journal of Mathematical Analysis and Applications 1992,165(2):333-345. 10.1016/0022-247X(92)90044-E
Acknowledgments
The authors are grateful for the referee's careful reviewing and helpful comments. Also the authors would like to thank Professor Su Jiabao for his helpful suggestions. This work is supported by NSFC(10871005) and BJJW(KM200610028001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, X., Wang, D. Multiple Periodic Solutions for Difference Equations with Double Resonance at Infinity. Adv Differ Equ 2011, 806458 (2011). https://doi.org/10.1155/2011/806458
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/806458
 and
and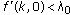 for
for  ,
,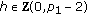 and
and for
for 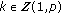 .
.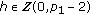 and
and with
with 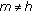 ,
,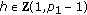 and
and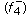 with
with 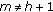 .
.