- Research Article
- Open access
- Published:
Existence of Pseudo-Almost Automorphic Mild Solutions to Some Nonautonomous Partial Evolution Equations
Advances in Difference Equations volume 2011, Article number: 895079 (2011)
Abstract
We use the Krasnoselskii fixed point principle to obtain the existence of pseudo almost automorphic mild solutions to some classes of nonautonomous partial evolutions equations in a Banach space.
1. Introduction
Let  be a Banach space. In the recent paper by Diagana [1], the existence of almost automorphic mild solutions to the nonautonomous abstract differential equations
be a Banach space. In the recent paper by Diagana [1], the existence of almost automorphic mild solutions to the nonautonomous abstract differential equations

where  for
for  is a family of closed linear operators with domains
is a family of closed linear operators with domains  satisfying Acquistapace-Terreni conditions, and the function
satisfying Acquistapace-Terreni conditions, and the function  is almost automorphic in
is almost automorphic in  uniformly in the second variable, was studied. For that, the author made extensive use of techniques utilized in [2], exponential dichotomy tools, and the Schauder fixed point theorem.
uniformly in the second variable, was studied. For that, the author made extensive use of techniques utilized in [2], exponential dichotomy tools, and the Schauder fixed point theorem.
In this paper we study the existence of pseudo-almost automorphic mild solutions to the nonautonomous partial evolution equations

where  for
for  is a family of linear operators satisfying Acquistpace-Terreni conditions and
is a family of linear operators satisfying Acquistpace-Terreni conditions and  are pseudo-almost automorphic functions. For that, we make use of exponential dichotomy tools as well as the well-known Krasnoselskii fixed point principle to obtain some reasonable sufficient conditions, which do guarantee the existence of pseudo-almost automorphic mild solutions to (1.2).
are pseudo-almost automorphic functions. For that, we make use of exponential dichotomy tools as well as the well-known Krasnoselskii fixed point principle to obtain some reasonable sufficient conditions, which do guarantee the existence of pseudo-almost automorphic mild solutions to (1.2).
The concept of pseudo-almost automorphy is a powerful generalization of both the notion of almost automorphy due to Bochner [3] and that of pseudo-almost periodicity due to Zhang (see [4]), which has recently been introduced in the literature by Liang et al. [5–7]. Such a concept, since its introduction in the literature, has recently generated several developments; see, for example, [8–12]. The question which consists of the existence of pseudo-almost automorphic solutions to abstract partial evolution equations has been made; see for instance [10, 11, 13]. However, the use of Krasnoselskii fixed point principle to establish the existence of pseudo-almost automorphic solutions to nonautonomous partial evolution equations in the form (1.2) is an original untreated problem, which is the main motivation of the paper.
The paper is organized as follows: Section 2 is devoted to preliminaries facts related to the existence of an evolution family. Some preliminary results on intermediate spaces are also stated there. Moreover, basic definitions and results on the concept of pseudo-almost automorphy are also given. Section 3 is devoted to the proof of the main result of the paper.
2. Preliminaries
Let  be a Banach space. If
be a Banach space. If  is a linear operator on the Banach space
is a linear operator on the Banach space  , then,
, then,  ,
,  ,
,  ,
,  , and
, and  stand, respectively, for its domain, resolvent, spectrum, null-space or kernel, and range. If
stand, respectively, for its domain, resolvent, spectrum, null-space or kernel, and range. If  is a linear operator, one sets
is a linear operator, one sets  for all
for all  .
.
If  are Banach spaces, then the space
are Banach spaces, then the space  denotes the collection of all bounded linear operators from
denotes the collection of all bounded linear operators from  into
into  equipped with its natural topology. This is simply denoted by
equipped with its natural topology. This is simply denoted by  when
when  . If
. If  is a projection, we set
is a projection, we set  .
.
2.1. Evolution Families
This section is devoted to the basic material on evolution equations as well the dichotomy tools. We follow the same setting as in the studies of Diagana [1].
Assumption (H.1) given below will be crucial throughout the paper.
(H.1)The family of closed linear operators  for
for  on
on  with domain
with domain  (possibly not densely defined) satisfy the so-called Acquistapace-Terreni conditions, that is, there exist constants
(possibly not densely defined) satisfy the so-called Acquistapace-Terreni conditions, that is, there exist constants  ,
,  ,
,  , and
, and  with
with  such that
such that

for  ,
,  .
.
It should mentioned that (H.1) was introduced in the literature by Acquistapace et al. in [14, 15] for  . Among other things, it ensures that there exists a unique evolution family
. Among other things, it ensures that there exists a unique evolution family

on  associated with
associated with  such that
such that  for all
for all  with
with  , and
, and
-
(a)
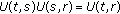 for
for  such that
such that  ;
; -
(b)
 for
for  where
where  is the identity operator of
is the identity operator of  ;
; -
(c)
 is continuous for
is continuous for 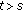 ;
; -
(d)
 ,
,  and
and (2.3)
(2.3)for
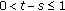 ,
, 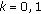 ;
; -
(e)
 for
for 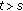 and
and 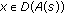 with
with 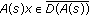 .
.
It should also be mentioned that the above-mentioned proprieties were mainly established in [16, Theorem 2.3] and [17, Theorem 2.1]; see also [15, 18]. In that case we say that  generates the evolution family
generates the evolution family  . For some nice works on evolution equations, which make use of evolution families, we refer the reader to, for example, [19–29].
. For some nice works on evolution equations, which make use of evolution families, we refer the reader to, for example, [19–29].
Definition 2.1.
One says that an evolution family  has an exponential dichotomy (or is hyperbolic) if there are projections
has an exponential dichotomy (or is hyperbolic) if there are projections  that are uniformly bounded and strongly continuous in
that are uniformly bounded and strongly continuous in  and constants
and constants  and
and  such that
such that
-
(f)
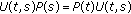 ;
; -
(g)
the restriction
 of
of 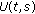 is invertible (we then set
is invertible (we then set 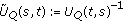 );
); -
(h)
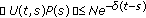 and
and 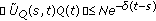 for
for  and
and 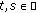 .
.
Under Acquistpace-Terreni conditions, the family of operators defined by

are called Green function corresponding to  and
and  .
.
This setting requires some estimates related to  . For that, we introduce the interpolation spaces for
. For that, we introduce the interpolation spaces for  . We refer the reader to the following excellent books [30–32] for proofs and further information on theses interpolation spaces.
. We refer the reader to the following excellent books [30–32] for proofs and further information on theses interpolation spaces.
Let  be a sectorial operator on
be a sectorial operator on  (for that, in assumption (H.1), replace
(for that, in assumption (H.1), replace  with
with  ) and let
) and let  . Define the real interpolation space
. Define the real interpolation space

which, by the way, is a Banach space when endowed with the norm  . For convenience we further write
. For convenience we further write

Moreover, let  of
of  . In particular, we have the following continuous embedding:
. In particular, we have the following continuous embedding:

for all  , where the fractional powers are defined in the usual way.
, where the fractional powers are defined in the usual way.
In general,  is not dense in the spaces
is not dense in the spaces  and
and  . However, we have the following continuous injection:
. However, we have the following continuous injection:

for  .
.
Given the family of linear operators  for
for  , satisfying (H.1), we set
, satisfying (H.1), we set

for  and
and  , with the corresponding norms.
, with the corresponding norms.
Now the embedding in (2.7) holds with constants independent of  . These interpolation spaces are of class
. These interpolation spaces are of class  [32, Definition 1.1.1], and hence there is a constant
[32, Definition 1.1.1], and hence there is a constant  such that
such that

We have the following fundamental estimates for the evolution family  .
.
Proposition 2.2 (see [33]).
Suppose that the evolution family  has exponential dichotomy. For
has exponential dichotomy. For  ,
,  , and
, and  , the following hold.
, the following hold.
-
(i)
There is a constant
 , such that
, such that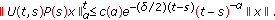 (2.11)
(2.11) -
(ii)
There is a constant
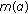 , such that
, such that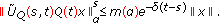 (2.12)
(2.12)
In addition to above, we also assume that the next assumption holds.
(H.2)The domain  is constant in
is constant in  . Moreover, the evolution family
. Moreover, the evolution family  generated by
generated by  has an exponential dichotomy with constants
has an exponential dichotomy with constants  and dichotomy projections
and dichotomy projections  for
for  .
.
2.2. Pseudo-Almost Automorphic Functions
Let  denote the collection of all
denote the collection of all  -valued bounded continuous functions. The space
-valued bounded continuous functions. The space  equipped with its natural norm, that is, the sup norm is a Banach space. Furthermore,
equipped with its natural norm, that is, the sup norm is a Banach space. Furthermore,  denotes the class of continuous functions from
denotes the class of continuous functions from  into
into  .
.
Definition 2.3.
A function  is said to be almost automorphic if, for every sequence of real numbers
is said to be almost automorphic if, for every sequence of real numbers  , there exists a subsequence
, there exists a subsequence  such that
such that

is well defined for each  , and
, and

for each  .
.
If the convergence above is uniform in  , then
, then  is almost periodic in the classical Bochner's sense. Denote by
is almost periodic in the classical Bochner's sense. Denote by  the collection of all almost automorphic functions
the collection of all almost automorphic functions  . Note that
. Note that  equipped with the sup-norm
equipped with the sup-norm  turns out to be a Banach space.
turns out to be a Banach space.
Among other things, almost automorphic functions satisfy the following properties.
Theorem 2.4 (see [34]).
If  , then
, then
-
(i)
 ,
, -
(ii)
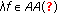 for any scalar
for any scalar  ,
, -
(iii)
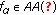 , where
, where  is defined by
is defined by 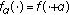 ,
, -
(iv)
the range
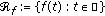 is relatively compact in
is relatively compact in  , thus
, thus  is bounded in norm,
is bounded in norm, -
(v)
if
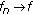 uniformly on
uniformly on  , where each
, where each 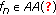 , then
, then 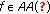 too.
too.
Let  be another Banach space.
be another Banach space.
Definition 2.5.
A jointly continuous function  is said to be almost automorphic in
is said to be almost automorphic in  if
if  is almost automorphic for all
is almost automorphic for all  (
( being any bounded subset). Equivalently, for every sequence of real numbers
being any bounded subset). Equivalently, for every sequence of real numbers  , there exists a subsequence
, there exists a subsequence  such that
such that

is well defined in  and for each
and for each  , and
, and

for all  and
and  .
.
The collection of such functions will be denoted by  .
.
For more on almost automorphic functions and related issues, we refer the reader to, for example, [1, 4, 9, 13, 34–39].
Define

Similarly,  will denote the collection of all bounded continuous functions
will denote the collection of all bounded continuous functions  such that
such that

uniformly in  , where
, where  is any bounded subset.
is any bounded subset.
Definition 2.6 (see Liang et al. [5, 6]).
A function  is called pseudo-almost automorphic if it can be expressed as
is called pseudo-almost automorphic if it can be expressed as  , where
, where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
The functions  and
and  appearing in Definition 2.6 are, respectively, called the almost automorphic and the ergodic perturbation components of
appearing in Definition 2.6 are, respectively, called the almost automorphic and the ergodic perturbation components of  .
.
Definition 2.7.
A bounded continuous function  belongs to
belongs to  whenever it can be expressed as
whenever it can be expressed as  , where
, where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
An important result is the next theorem, which is due to Xiao et al. [6].
Theorem 2.8 (see [6]).
The space  equipped with the sup norm
equipped with the sup norm  is a Banach space.
is a Banach space.
The next composition result, that is Theorem 2.9, is a consequence of [12, Theorem 2.4].
Theorem 2.9.
Suppose that  belongs to
belongs to  , with
, with  being uniformly continuous on any bounded subset
being uniformly continuous on any bounded subset  of
of  uniformly in
uniformly in  . Furthermore, one supposes that there exists
. Furthermore, one supposes that there exists  such that
such that

for all  and
and  .
.
Then the function defined by  belongs to
belongs to  provided
provided  .
.
We also have the following.
Theorem 2.10 (see [6]).
If  belongs to
belongs to  and if
and if  is uniformly continuous on any bounded subset
is uniformly continuous on any bounded subset  of
of  for each
for each  , then the function defined by
, then the function defined by  belongs to
belongs to  provided that
provided that  .
.
3. Main Results
Throughout the rest of the paper we fix  , real numbers, satisfying
, real numbers, satisfying  with
with  .
.
To study the existence of pseudo-almost automorphic solutions to (1.2), in addition to the previous assumptions, we suppose that the injection

is compact, and that the following additional assumptions hold:
(H.3) . Moreover, for any sequence of real numbers
. Moreover, for any sequence of real numbers  there exist a subsequence
there exist a subsequence  and a well-defined function
and a well-defined function  such that for each
such that for each  , one can find
, one can find  such that
such that

whenever  for
for  , and
, and

whenever  for all
for all  , where
, where  with
with  .
.
(H.4)
-
(a)
The function
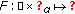 is pseudo-almost automorphic in the first variable uniformly in the second one. The function
is pseudo-almost automorphic in the first variable uniformly in the second one. The function 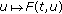 is uniformly continuous on any bounded subset
is uniformly continuous on any bounded subset 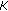 of
of  for each
for each 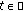 . Finally,
. Finally, 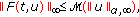 (3.4)
(3.4)
where  and
and  is a continuous, monotone increasing function satisfying
is a continuous, monotone increasing function satisfying

-
(b)
The function
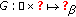 is pseudo-almost automorphic in the first variable uniformly in the second one. Moreover,
is pseudo-almost automorphic in the first variable uniformly in the second one. Moreover,  is globally Lipschitz in the following sense: there exists
is globally Lipschitz in the following sense: there exists  for which
for which  (3.6)
(3.6)
for all  and
and  .
.
(H.5)The operator  is invertible for each
is invertible for each  , that is,
, that is,  for each
for each  . Moreover, there exists
. Moreover, there exists  such that
such that

To study the existence and uniqueness of pseudo-almost automorphic solutions to (1.2) we first introduce the notion of a mild solution, which has been adapted to the one given in the studies of Diagana et al. [35, Definition 3.1].
Definition 3.1.
A continuous function  is said to be a mild solution to (1.2) provided that the function
is said to be a mild solution to (1.2) provided that the function  is integrable on
is integrable on  , the function
, the function  is integrable on
is integrable on  and
and

for  and for all
and for all  .
.
Under assumptions (H.1), (H.2), and (H.5), it can be readily shown that (1.2) has a mild solution given by

for each  .
.
We denote by  and
and  the nonlinear integral operators defined by
the nonlinear integral operators defined by

The main result of the present paper will be based upon the use of the well-known fixed point theorem of Krasnoselskii given as follows.
Theorem 3.2.
Let  be a closed bounded convex subset of a Banach space
be a closed bounded convex subset of a Banach space  . Suppose the (possibly nonlinear) operators
. Suppose the (possibly nonlinear) operators  and
and  map
map  into
into  satisfying
satisfying
-
(1)
for all
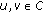 , then
, then 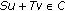 ;
; -
(2)
the operator
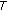 is a contraction;
is a contraction; -
(3)
the operator
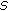 is continuous and
is continuous and  is contained in a compact set.
is contained in a compact set.
Then there exists  such that
such that  .
.
We need the following new technical lemma.
Lemma 3.3.
For each  , suppose that assumptions (H.1), (H.2) hold, and let
, suppose that assumptions (H.1), (H.2) hold, and let  be real numbers such that
be real numbers such that  with
with  . Then there are two constants
. Then there are two constants  such that
such that


Proof.
Let  . First of all, note that
. First of all, note that  for all
for all  ,
,  such that
such that  and
and  .
.
Letting  and using (H.2) and the above-mentioned approximate, we obtain
and using (H.2) and the above-mentioned approximate, we obtain

Now since  as
as  , it follows that there exists
, it follows that there exists  such that
such that

Now, let  . Using (2.11) and the fact
. Using (2.11) and the fact  , we obtain
, we obtain

In summary, there exists  such that
such that

for all  with
with  .
.
Let  . Since the restriction of
. Since the restriction of  to
to  is a bounded linear operator it follows that
is a bounded linear operator it follows that

for  by using (2.12).
by using (2.12).
A straightforward consequence of Lemma 3.3 is the following.
Corollary 3.4.
For each  , suppose that assumptions (H.1), (H.2), and (H.5) hold, and let
, suppose that assumptions (H.1), (H.2), and (H.5) hold, and let  be real numbers such that
be real numbers such that  with
with  . Then there are two constants
. Then there are two constants  such that
such that


Proof.
We make use of (H.5) and Lemma 3.3. Indeed, for each  ,
,

Equation (3.19) has already been proved (see the proof of (3.12)).
Lemma 3.5.
Under assumptions (H.1), (H.2), (H.3), and (H.4), the mapping  is well defined and continuous.
is well defined and continuous.
Proof.
We first show that  . For that, let
. For that, let  and
and  be the integral operators defined, respectively, by
be the integral operators defined, respectively, by

Now, using (2.11) it follows that for all  ,
,

and hence

where  .
.
It remains to prove that  is continuous. For that consider an arbitrary sequence of functions
is continuous. For that consider an arbitrary sequence of functions  which converges uniformly to some
which converges uniformly to some  , that is,
, that is,  .
.
Now

Now, using the continuity of  and the Lebesgue Dominated Convergence Theorem we conclude that
and the Lebesgue Dominated Convergence Theorem we conclude that

and hence  as
as  .
.
The proof for  is similar to that of
is similar to that of  and hence omitted. For
and hence omitted. For  , one makes use of (2.12) rather than (2.11).
, one makes use of (2.12) rather than (2.11).
Lemma 3.6.
Under assumptions (H.1), (H.2), (H.3), and (H.4), the integral operator  defined above maps
defined above maps  into itself.
into itself.
Proof.
Let  . Setting
. Setting  and using Theorem 2.10 it follows that
and using Theorem 2.10 it follows that  . Let
. Let  , where
, where  and
and  . Let us show that
. Let us show that  . Indeed, since
. Indeed, since  , for every sequence of real numbers
, for every sequence of real numbers  there exists a subsequence
there exists a subsequence  such that
such that

is well defined for each  and
and

for each  .
.
Set  and
and  for all
for all  .
.
Now

Using (2.11) and the Lebesgue Dominated Convergence Theorem, one can easily see that

Similarly, using (H.3) and [40] it follows that

Therefore,

Using similar ideas as the previous ones, one can easily see that

Again using (2.11) it follows that

Set

Since  is translation invariant it follows that
is translation invariant it follows that  belongs to
belongs to  for each
for each  , and hence
, and hence

for each  .
.
One completes the proof by using the well-known Lebesgue dominated convergence theorem and the fact  as
as  for each
for each  .
.
The proof for  is similar to that of
is similar to that of  and hence omitted. For
and hence omitted. For  , one makes use of (2.12) rather than (2.11).
, one makes use of (2.12) rather than (2.11).
Let  , and let
, and let  , where
, where

Clearly, the space  equipped with the norm
equipped with the norm  is a Banach space, which is the Banach space of all bounded continuous Hölder functions from
is a Banach space, which is the Banach space of all bounded continuous Hölder functions from  to
to  whose Hölder exponent is
whose Hölder exponent is  .
.
Lemma 3.7.
Under assumptions (H.1), (H.2), (H.3), (H.4), and (H.5),  maps bounded sets of
maps bounded sets of  into bounded sets of
into bounded sets of  for some
for some  , where
, where  ,
,  are the integral operators introduced previously.
are the integral operators introduced previously.
Proof.
Let  , and let
, and let  for each
for each  . Then we have
. Then we have

and hence

Similarly,

and hence

Let  . Clearly,
. Clearly,

Clearly,

Similarly,

Now

where  is a positive constant.
is a positive constant.
Consequently, letting  it follows that
it follows that

where  is a positive constant.
is a positive constant.
Therefore, for each  such that
such that

for all  , then
, then  belongs to
belongs to  with
with

for all  , where
, where  depends on
depends on  .
.
The proof of the next lemma follows along the same lines as that of Lemma 3.6 and hence omitted.
Lemma 3.8.
The integral operator  maps bounded sets of
maps bounded sets of  into bounded sets of
into bounded sets of  .
.
Similarly, the next lemma is a consequence of [2, Proposition 3.3].
Lemma 3.9.
The set  is compactly contained in
is compactly contained in  , that is, the canonical injection
, that is, the canonical injection  is compact, which yields
is compact, which yields

is compact, too.
Theorem 3.10.
Suppose that assumptions (H.1), (H.2), (H.3), (H.4), and (H.5) hold, then the operator  defined by
defined by  is compact.
is compact.
Proof.
The proof follows along the same lines as that of [2, Proposition 3.4]. Recalling that in view of Lemma 3.7, we have

for all  ,
,  with
with  , where
, where  are positive constants. Consequently,
are positive constants. Consequently,  and
and  yield
yield  and
and

where  .
.
Therefore, there exists  such that for all
such that for all  , the following hold:
, the following hold:

In view of the above, it follows that  is continuous and compact, where
is continuous and compact, where  is the ball in
is the ball in  of radius
of radius  with
with  .
.
Define

for all  .
.
Lemma 3.11.
Under assumptions (H.1), (H.2), (H.3), (H.4), and (H.5), the integral operators  and
and  defined above map
defined above map  into itself.
into itself.
Proof.
Let  . Again, using the composition of pseudo-almost automorphic functions (Theorem 2.10) it follows that
. Again, using the composition of pseudo-almost automorphic functions (Theorem 2.10) it follows that  is in
is in  whenever
whenever  . In particular,
. In particular,

Now write  , where
, where  and
and  , that is,
, that is,  where
where

Clearly,  . Indeed, since
. Indeed, since  , for every sequence of real numbers
, for every sequence of real numbers  there exists a subsequence
there exists a subsequence  such that
such that

is well defined for each  and
and

for each  .
.
Set  and
and  for all
for all  .
.
Now

Using (3.18) and the Lebesgue Dominated Convergence Theorem, one can easily see that

Similarly, using (H.3) it follows that

Therefore,

Using similar ideas as the previous ones, one can easily see that

Now, let  . Again from (3.18), we have
. Again from (3.18), we have

Now

as  for every
for every  . One completes the proof by using the Lebesgue's dominated convergence theorem.
. One completes the proof by using the Lebesgue's dominated convergence theorem.
The proof for  is similar to that of
is similar to that of  except that one makes use of (3.19) instead of (3.18).
except that one makes use of (3.19) instead of (3.18).
Theorem 3.12.
Under assumptions (H.1), (H.2), (H.3), (H.4), and (H.5) and if  is small enough, then (1.2) has at least one pseudo-almost automorphic solution.
is small enough, then (1.2) has at least one pseudo-almost automorphic solution.
Proof.
We have seen in the proof of Theorem 3.10 that  is continuous and compact, where
is continuous and compact, where  is the ball in
is the ball in  of radius
of radius  with
with  .
.
Now, if we set  it follows that
it follows that

for all  .
.
Choose  such that
such that

and let  be the closed ball in
be the closed ball in  of radius
of radius  . It is then clear that
. It is then clear that

for all  and hence
and hence  .
.
To complete the proof we have to show that  is a strict contraction. Indeed, for all
is a strict contraction. Indeed, for all 

and hence  is a strict contraction whenever
is a strict contraction whenever  is small enough.
is small enough.
Using the Krasnoselskii fixed point theorem (Theorem 3.2) it follows that there exists at least one pseudo-almost automorphic mild solution to (1.2).
References
Diagana T: Almost automorphic mild solutions to some classes of nonautonomous higher-order differential equations. Semigroup Forum. In press
Goldstein JA, N'Guérékata GM: Almost automorphic solutions of semilinear evolution equations. Proceedings of the American Mathematical Society 2005,133(8):2401-2408. 10.1090/S0002-9939-05-07790-7
Bochner S: Continuous mappings of almost automorphic and almost periodic functions. Proceedings of the National Academy of Sciences of the United States of America 1964, 52: 907-910. 10.1073/pnas.52.4.907
Diagana T: Pseudo Almost Periodic Functions in Banach Spaces. Nova Science, New York, NY, USA; 2007:xiv+132.
Liang J, Zhang J, Xiao T-J: Composition of pseudo almost automorphic and asymptotically almost automorphic functions. Journal of Mathematical Analysis and Applications 2008,340(2):1493-1499. 10.1016/j.jmaa.2007.09.065
Xiao T-J, Liang J, Zhang J: Pseudo almost automorphic solutions to semilinear differential equations in Banach spaces. Semigroup Forum 2008,76(3):518-524. 10.1007/s00233-007-9011-y
Xiao T-J, Zhu X-X, Liang J: Pseudo-almost automorphic mild solutions to nonautonomous differential equations and applications. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):4079-4085. 10.1016/j.na.2008.08.018
Cieutat P, Ezzinbi K: Existence, uniqueness and attractiveness of a pseudo almost automorphic solutions for some dissipative differential equations in Banach spaces. Journal of Mathematical Analysis and Applications 2009,354(2):494-506. 10.1016/j.jmaa.2009.01.016
Diagana T:Existence of pseudo-almost automorphic solutions to some abstract differential equations with
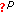 -pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034Ezzinbi K, Fatajou S, N'guérékata GM: Pseudo-almost-automorphic solutions to some neutral partial functional differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1641-1647. 10.1016/j.na.2008.02.039
Ezzinbi K, Fatajou S, N'Guérékata GM: Pseudo almost automorphic solutions for dissipative differential equations in Banach spaces. Journal of Mathematical Analysis and Applications 2009,351(2):765-772. 10.1016/j.jmaa.2008.11.017
Liang J, N'Guérékata GM, Xiao T-J, Zhang J: Some properties of pseudo-almost automorphic functions and applications to abstract differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009,70(7):2731-2735. 10.1016/j.na.2008.03.061
Diagana T: Pseudo-almost automorphic solutions to some classes of nonautonomous partial evolution equations. Differential Equations & Applications 2009,1(4):561-582.
Acquistapace P, Flandoli F, Terreni B: Initial-boundary value problems and optimal control for nonautonomous parabolic systems. SIAM Journal on Control and Optimization 1991,29(1):89-118. 10.1137/0329005
Acquistapace P, Terreni B: A unified approach to abstract linear nonautonomous parabolic equations. Rendiconti del Seminario Matematico della Università di Padova 1987, 78: 47-107.
Acquistapace P: Evolution operators and strong solutions of abstract linear parabolic equations. Differential and Integral Equations 1988,1(4):433-457.
Yagi A: Abstract quasilinear evolution equations of parabolic type in Banach spaces. Bollettino dell'Unione Matematica Italiana B 1991,5(2):341-368.
Yagi A: Parabolic evolution equations in which the coefficients are the generators of infinitely differentiable semigroups. II. Funkcialaj Ekvacioj 1990,33(1):139-150.
Arendt W, Chill R, Fornaro S, Poupaud C:
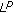 -maximal regularity for non-autonomous evolution equations. Journal of Differential Equations 2007,237(1):1-26. 10.1016/j.jde.2007.02.010
-maximal regularity for non-autonomous evolution equations. Journal of Differential Equations 2007,237(1):1-26. 10.1016/j.jde.2007.02.010Arendt W, Batty CJK: Almost periodic solutions of first- and second-order Cauchy problems. Journal of Differential Equations 1997,137(2):363-383. 10.1006/jdeq.1997.3266
Chicone C, Latushkin Y: Evolution Semigroups in Dynamical Systems and Differential Equations, Mathematical Surveys and Monographs. Volume 70. American Mathematical Society, Providence, RI, USA; 1999:x+361.
Ding H-S, Liang J, N'Guérékata GM, Xiao T-J: Pseudo-almost periodicity of some nonautonomous evolution equations with delay. Nonlinear Analysis: Theory, Methods & Applications 2007,67(5):1412-1418. 10.1016/j.na.2006.07.026
Liang J, Nagel R, Xiao T-J: Nonautonomous heat equations with generalized Wentzell boundary conditions. Journal of Evolution Equations 2003,3(2):321-331.
Liang J, Xiao T-J: Solutions to nonautonomous abstract functional equations with infinite delay. Taiwanese Journal of Mathematics 2006,10(1):163-172.
Maniar L, Schnaubelt R: Almost periodicity of inhomogeneous parabolic evolution equations. In Evolution Equations, Search ResultsLecture Notes in Pure and Applied Mathematics. Volume 234. Dekker, New York, NY, USA; 2003:299-318.
Schnaubelt R: Asymptotically autonomous parabolic evolution equations. Journal of Evolution Equations 2001,1(1):19-37. 10.1007/PL00001363
Schnaubelt R: Asymptotic behaviour of parabolic nonautonomous evolution equations. In Functional Analytic Methods for Evolution Equations, Lecture Notes in Mathematics. Volume 1855. Springer, Berlin, Germany; 2004:401-472.
Xiao T-J, Liang J: Existence of classical solutions to nonautonomous nonlocal parabolic problems. Nonlinear Analysis, Theory, Methods and Applications 2005,63(5–7):e225-e232.
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Amann H: Linear and Quasilinear Parabolic Problems, Monographs in Mathematics. Volume 89. Birkhäuser, Boston, Mass, USA; 1995:xxxvi+335.
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Lunardi A: Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and Their Applications. Volume 16. Birkhäuser, Basel, Switzerland; 1995:xviii+424.
Baroun M, Boulite S, Diagana T, Maniar L: Almost periodic solutions to some semilinear non-autonomous thermoelastic plate equations. Journal of Mathematical Analysis and Applications 2009,349(1):74-84. 10.1016/j.jmaa.2008.08.034
N'Guerekata GM: Almost Automorphic and Almost Periodic Functions in Abstract Spaces. Kluwer Academic/Plenum Publishers, New York, NY, USA; 2001:x+138.
Diagana T, Hernández E, Rabello M: Pseudo almost periodic solutions to some non-autonomous neutral functional differential equations with unbounded delay. Mathematical and Computer Modelling 2007,45(9-10):1241-1252. 10.1016/j.mcm.2006.10.006
Diagana T: Stepanov-like pseudo almost periodic functions and their applications to differential equations. Communications in Mathematical Analysis 2007,3(1):9-18.
Diagana T: Stepanov-like pseudo-almost periodicity and its applications to some nonautonomous differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4277-4285. 10.1016/j.na.2007.10.051
Diagana T: Existence of almost automorphic solutions to some classes of nonautonomous higher-order differential equations. Electronic Journal of Qualitative Theory of Differential Equations 2010, (22):1-26.
Diagana T:Existence of pseudo-almost automorphic solutions to some abstract differential equations with
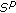 -pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034Baroun M, Boulite S, N'Guérékata GM, Maniar L: Almost automorphy of semilinear parabolic evolution equations. Electronic Journal of Differential Equations 2008,2008(60):1-9.
Acknowledgment
The author would like to express his thanks to the referees for careful reading of the paper and insightful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diagana, T. Existence of Pseudo-Almost Automorphic Mild Solutions to Some Nonautonomous Partial Evolution Equations. Adv Differ Equ 2011, 895079 (2011). https://doi.org/10.1155/2011/895079
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/895079
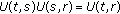 for
for  such that
such that  ;
; for
for  where
where  is the identity operator of
is the identity operator of  ;
; is continuous for
is continuous for 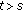 ;
; ,
,  and
and
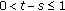 ,
, 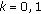 ;
; for
for 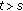 and
and 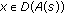 with
with 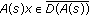 .
.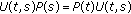 ;
; of
of 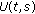 is invertible (we then set
is invertible (we then set 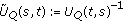 );
);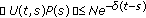 and
and 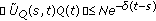 for
for  and
and 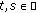 .
. , such that
, such that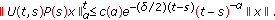
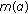 , such that
, such that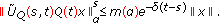
 ,
,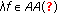 for any scalar
for any scalar  ,
,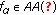 , where
, where  is defined by
is defined by 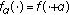 ,
,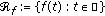 is relatively compact in
is relatively compact in  , thus
, thus  is bounded in norm,
is bounded in norm,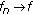 uniformly on
uniformly on  , where each
, where each 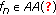 , then
, then 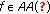 too.
too.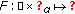 is pseudo-almost automorphic in the first variable uniformly in the second one. The function
is pseudo-almost automorphic in the first variable uniformly in the second one. The function 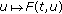 is uniformly continuous on any bounded subset
is uniformly continuous on any bounded subset 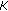 of
of  for each
for each 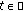 . Finally,
. Finally, 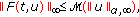
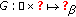 is pseudo-almost automorphic in the first variable uniformly in the second one. Moreover,
is pseudo-almost automorphic in the first variable uniformly in the second one. Moreover,  is globally Lipschitz in the following sense: there exists
is globally Lipschitz in the following sense: there exists  for which
for which 
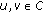 , then
, then 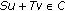 ;
;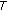 is a contraction;
is a contraction;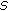 is continuous and
is continuous and  is contained in a compact set.
is contained in a compact set.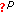 -pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034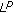 -maximal regularity for non-autonomous evolution equations. Journal of Differential Equations 2007,237(1):1-26. 10.1016/j.jde.2007.02.010
-maximal regularity for non-autonomous evolution equations. Journal of Differential Equations 2007,237(1):1-26. 10.1016/j.jde.2007.02.010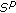 -pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034