- Research Article
- Open access
- Published:
Notes on Interpolation Inequalities
Advances in Difference Equations volume 2011, Article number: 913403 (2011)
Abstract
An easy proof of the John-Nirenberg inequality is provided by merely using the Calderón-Zygmund decomposition. Moreover, an interpolation inequality is presented with the help of the John-Nirenberg inequality.
1. Introduction
It is well known that various interpolation inequalities play an important role in the study of operational equations, partial differential equations, and variation problems (see, e.g., [1–6]). So, it is an issue worthy of deep investigation.
Let  be either
be either  or a fixed cube in
or a fixed cube in  . For
. For  , write
, write

where the supremum is taken over all cubes  and
and  .
.
Recall that  is the set consisting of all locally integrable functions on
is the set consisting of all locally integrable functions on  such that
such that  , which is a Banach space endowed with the norm
, which is a Banach space endowed with the norm  . It is clear that any bounded function on
. It is clear that any bounded function on  is in
is in  , but the converse is not true. On the other hand, the BMO space is regarded as a natural substitute for
, but the converse is not true. On the other hand, the BMO space is regarded as a natural substitute for  in many studies. One of the important features of the space is the John-Nirenberg inequality. There are several versions of its proof; see, for example, [2, 7–9]. Stimulated by these works, we give, in this paper, an easy proof of the John-Nirenberg inequality by using the Calderón-Zygmund decomposition only. Moreover, with the help of this inequality, an interpolation inequality is showed for
in many studies. One of the important features of the space is the John-Nirenberg inequality. There are several versions of its proof; see, for example, [2, 7–9]. Stimulated by these works, we give, in this paper, an easy proof of the John-Nirenberg inequality by using the Calderón-Zygmund decomposition only. Moreover, with the help of this inequality, an interpolation inequality is showed for  and BMO norms.
and BMO norms.
2. Results and Proofs
Lemma 2.1 (John-Nirenberg inequality).
If  , then there exist positive constants
, then there exist positive constants  ,
,  such that, for each cube
such that, for each cube  ,
,

Proof.
Without loss of generality, we can and do assume that  .
.
For each  , let
, let  denote the least number for which we have
denote the least number for which we have

for any cube  . It is easy to see that
. It is easy to see that 
 and
and  is decreasing.
is decreasing.
Fix a cube  . Applying the Calderón-Zygmund decomposition (cf., e.g., [2, 9]) to
. Applying the Calderón-Zygmund decomposition (cf., e.g., [2, 9]) to  on
on  , with
, with  as the separating number, we get a sequence of disjoint cubes
as the separating number, we get a sequence of disjoint cubes  and
and  such that
such that



Using (2.5), we have

From (2.3), (2.4), and (2.6), we deduce that for  ,
,

This yields that

Let  ,
,  . Then
. Then  . By iterating, we get
. By iterating, we get

Thus, letting

gives that

since

This completes the proof.
Remark 2.2.
-
(1)
As we have seen, the recursive estimation (2.8) justifies the desired exponential decay of
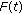 .
. -
(2)
There exists a gap in the proof of the John-Nirenberg inequality given in [2]. Actually, for a decreasing function
 , the following estimate:
, the following estimate:  (2.13)
(2.13)
does not generally imply such a property, that is, the existence of constants  such that
such that

We present the following function as a counter example:

In fact, it is easy to see that there are no constants  such that (2.14) holds. On the other hand, we have
such that (2.14) holds. On the other hand, we have

Integrating both sides of the above equation from  to
to  , we obtain
, we obtain

where the fact that

is used to get the first inequality above. This means that

Next, we make use of the John-Nirenberg inequality to obtain an interpolation inequality for  and BMO norms.
and BMO norms.
Theorem 2.3.
Suppose that  and
and  . Then we have
. Then we have

Proof.
If  , the proof is trivial; so we assume that
, the proof is trivial; so we assume that  . In view of the Calderón-Zygmund decomposition theorem, there exists a sequence of disjoint cubes
. In view of the Calderón-Zygmund decomposition theorem, there exists a sequence of disjoint cubes  and
and  such that
such that



From (2.23), we get

Using (2.21)–(2.24), together with Lemma 2.1, yields that, for  ,
,

From (2.25), we obtain

Hence, the proof is complete.
References
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Classics in Mathematics. Springer, Berlin, Germany; 2001:xiv+517.
Han YS: Mordern Harmonic Analysis Methods and Applications. Science Press, Beijing, China; 1997.
Triebel H: Interpolation Theory, Function Spaces, Differential Operators, North-Holland Mathematical Library. Volume 18. North-Holland, Amsterdam, The Netherlands; 1978:528.
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Complete second order differential equations in Banach spaces with dynamic boundary conditions. Journal of Differential Equations 2004,200(1):105-136. 10.1016/j.jde.2004.01.011
Xiao T-J, Liang J: Second order parabolic equations in Banach spaces with dynamic boundary conditions. Transactions of the American Mathematical Society 2004,356(12):4787-4809. 10.1090/S0002-9947-04-03704-3
George C: Exercises in Integration. Springer, New York, NY, USA; 1984:x+550.
John F, Nirenberg L: On functions of bounded mean oscillation. Communications on Pure and Applied Mathematics 1961, 14: 415-426. 10.1002/cpa.3160140317
Stein EliasM: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series. Volume 43. Princeton University Press, Princeton, NJ, NY, USA; 1993:xiv+695.
Acknowledgments
The authors would like to thank the referees for helpful comments and suggestions. The work was supported partly by the NSF of China (11071042) and the Research Fund for Shanghai Key Laboratory for Contemporary Applied Mathematics (08DZ2271900).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dong, JG., Xiao, TJ. Notes on Interpolation Inequalities. Adv Differ Equ 2011, 913403 (2011). https://doi.org/10.1155/2011/913403
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/913403
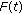 .
. , the following estimate:
, the following estimate: 