- Research Article
- Open access
- Published:
Existence of Solutions to Anti-Periodic Boundary Value Problem for Nonlinear Fractional Differential Equations with Impulses
Advances in Difference Equations volume 2011, Article number: 915689 (2011)
Abstract
This paper discusses the existence of solutions to antiperiodic boundary value problem for nonlinear impulsive fractional differential equations. By using Banach fixed point theorem, Schaefer fixed point theorem, and nonlinear alternative of Leray-Schauder type theorem, some existence results of solutions are obtained. An example is given to illustrate the main result.
1. Introduction
In this paper, we consider an antiperiodic boundary value problem for nonlinear fractional differential equations with impulses

where  is a positive constant,
is a positive constant,  ,
,  denotes the Caputo fractional derivative of order
denotes the Caputo fractional derivative of order  ,
,  ,
,  ,
,  and
and  satisfy that
satisfy that  ,
,  ,
,  ,
,  and
and  represent the right and left limits of
represent the right and left limits of  at
at  .
.
Fractional differential equations have proved to be an excellent tool in the mathematic modeling of many systems and processes in various fields of science and engineering. Indeed, we can find numerous applications in viscoelasticity, electrochemistry, control, electromagnetic, porous media, and so forth. In consequence, the subject of fractional differential equations is gaining much importance and attention (see [1–6] and the references therein).
The theory of impulsive differential equations has found its extensive applications in realistic mathematic modeling of a wide variety of practical situations and has emerged as an important area of investigation in recent years. For the general theory of impulsive differential equations, we refer the reader to [7, 8]. Recently, many authors are devoted to the study of boundary value problems for impulsive differential equations of integer order, see [9–12].
Very recently, there are only a few papers about the nonlinear impulsive differential equations and delayed differential equations of fractional order.
Agarwal et al. in [13] have established some sufficient conditions for the existence of solutions for a class of initial value problems for impulsive fractional differential equations involving the Caputo farctional derivative. Ahmad et al. in [14] have discussed some existence results for the two-point boundary value problem involving nonlinear impulsive hybrid differential equation of fractional order by means of contraction mapping principle and Krasnoselskii's fixed point theorem. By the similar way, they have also obtained the existence results for integral boundary value problem of nonlinear impulsive fractional differential equations (see [15]). Tian et al. in [16] have obtained some existence results for the three-point impulsive boundary value problem involving fractional differential equations by the means of fixed points method. Maraaba et al. in [17, 18] have established the existence and uniqueness theorem for the delay differential equations with Caputo fractional derivatives. Wang et al. in [19] have studied the existence and uniqueness of the mild solution for a class of impulsive fractional differential equations with time-varying generating operators and nonlocal conditions.
To the best of our knowledge, few papers exist in the literature devoted to the antiperiodic boundary value problem for fractional differential equations with impulses. This paper studies the existence of solutions of antiperiodic boundary value problem for fractional differential equations with impulses.
The organization of this paper is as follows. In Section 2, we recall some definitions of fractional integral and derivative and preliminary results which will be used in this paper. In Section 3, we will consider the existence results for problem (1.1). We give three results, the first one is based on Banach fixed theorem, the second one is based on Schaefer fixed point theorem, and the third one is based on the nonlinear alternative of Leray-Schauder type. In Section 4, we will give an example to illustrate the main result.
2. Preliminaries
In this section, we present some basic notations, definitions, and preliminary results which will be used throughout this paper.
Definition 2.1 (see [4]).
The Caputo fractional derivative of order  of a function
of a function  is defined as
is defined as

where  denotes the integer part of the real number
denotes the integer part of the real number  .
.
Definition 2.2 (see [4]).
The Riemann-Liouville fractional integral of order  of a function
of a function  ,
,  , is defined as
, is defined as

provided that the right side is pointwise defined on  .
.
Definition 2.3 (see [4]).
The Riemann-Liouville fractional derivative of order  of a continuous function
of a continuous function  is given by
is given by

where  and
and  denotes the integer part of real number
denotes the integer part of real number  , provided that the right side is pointwise defined on
, provided that the right side is pointwise defined on  .
.
For the sake of convenience, we introduce the following notation.
Let  .
.  . We define
. We define  and
and  exists, and
exists, and  . Obviously,
. Obviously,  is a Banach space with the norm
is a Banach space with the norm  .
.
Definition 2.4.
A function  is said to be a solution of (1.1) if
is said to be a solution of (1.1) if  satisfies the equation
satisfies the equation  for
for  , the equations
, the equations  ,
,  , and the condition
, and the condition  .
.
Lemma 2.5 (see [20]).
Let  ; then
; then

for some  ,
,  .
.
Lemma 2.6 (nonlinear alternative of Leray-Schauder type [21]).
Let  be a Banach space with
be a Banach space with  closed and convex. Assume that
closed and convex. Assume that  is a relatively open subset of
is a relatively open subset of  with
with  and
and  is continuous, compact map. Then either
is continuous, compact map. Then either
-
(1)
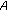 has a fixed point in
has a fixed point in 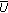 , or
, or -
(2)
there exists
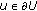 and
and  with
with 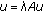 .
.
Lemma 2.7 (Schaefer fixed point theorem [22]).
Let  be a convex subset of a normed linear space
be a convex subset of a normed linear space  and
and  . Let
. Let  be a completely continuous operator, and let
be a completely continuous operator, and let

Then either  is unbounded or
is unbounded or  has a fixed point.
has a fixed point.
Lemma 2.8.
Assume that  . A function
. A function  is a solution of the antiperiodic boundary value problem
is a solution of the antiperiodic boundary value problem

if and only if  is a solution of the integral equation
is a solution of the integral equation

Proof.
Assume that  satisfies (2.6). Using Lemma 2.5, for some constants
satisfies (2.6). Using Lemma 2.5, for some constants  , we have
, we have

Then, we obtain

If  , then we have
, then we have

where  are arbitrary constants. Thus, we find that
are arbitrary constants. Thus, we find that

In view of  and
and  , we have
, we have

Hence, we obtain

Repeating the process in this way, the solution  for
for  can be written as
can be written as

On the other hand, by (2.14), we have

By the boundary conditions  , we obtain
, we obtain

Substituting the values of  and
and  into (2.8), (2.14), respectively, we obtain (2.7).
into (2.8), (2.14), respectively, we obtain (2.7).
Conversely, we assume that  is a solution of the integral equation (2.7). By a direct computation, it follows that the solution given by (2.7) satisfies (2.6). The proof is completed.
is a solution of the integral equation (2.7). By a direct computation, it follows that the solution given by (2.7) satisfies (2.6). The proof is completed.
3. Main Result
In this section, our aim is to discuss the existence and uniqueness of solutions to the problem (1.1).
Theorem 3.1.
Assume that
there exists a constant  such that
such that  , for each
, for each  and all
and all  ;
;
there exist constants  such that
such that  ,
,  , for each
, for each  and all
and all  .
.
If

then problem (1.1) has a unique solution on  .
.
Proof.
We transform the problem (1.1) into a fixed point problem. Define an operator  by
by

where  is with the norm
is with the norm  . Let
. Let  ; then for each
; then for each  , we have
, we have

Therefore,

Since

consequently  is a contraction; as a consequence of Banach fixed point theorem, we deduce that
is a contraction; as a consequence of Banach fixed point theorem, we deduce that  has a fixed point which is a solution of the problem (1.1).
has a fixed point which is a solution of the problem (1.1).
Theorem 3.2.
Assume that
the function  is continuous and there exists a constant
is continuous and there exists a constant  such that
such that  for each
for each  and all
and all  ;
;
the functions  are continuous and there exist constants
are continuous and there exist constants  such that
such that  ,
,  , for all
, for all  ,
,  .
.
Then the problem (1.1) has at least one solution on  .
.
Proof.
We will use Schaefer fixed-point theorem to prove  has a fixed point. The proof will be given in several steps.
has a fixed point. The proof will be given in several steps.
Step 1.
 is continuous.
is continuous.
Let  be a sequence such that
be a sequence such that  in
in  ; we have
; we have

Since  are continuous functions, then we have
are continuous functions, then we have

Step 2.
 maps bounded sets into bounded sets in
maps bounded sets into bounded sets in  .
.
Indeed, it is enough to show that for any  , there exists a positive constant
, there exists a positive constant  such that, for each
such that, for each  , we have
, we have  . By
. By  and
and  , for each
, for each  , we can obtain
, we can obtain

Therefore,

Step 3.
 maps bounded sets into equicontinuous sets in
maps bounded sets into equicontinuous sets in  .
.
Let  be a bounded set of
be a bounded set of  as in Step 2, and let
as in Step 2, and let  . For each
. For each  , we can estimate the derivative
, we can estimate the derivative  :
:

Hence, let  ; we have
; we have

So  is equicontinuous in
is equicontinuous in  . As a consequence of Steps 1 to 3 together with the Arzela-Ascoli theorem, we can conclude that
. As a consequence of Steps 1 to 3 together with the Arzela-Ascoli theorem, we can conclude that  is completely continuous.
is completely continuous.
Step 4.
A priori bounds.
Now it remains to show that the set

is bounded. Let  for some
for some  . Thus, for each
. Thus, for each  , we have
, we have

For each  , by
, by  and
and  , we have
, we have

This shows that the set  is bounded. As a consequence of Schaefer fixed-point theorem, we deduce that
is bounded. As a consequence of Schaefer fixed-point theorem, we deduce that  has a fixed point which is a solution of the problem (1.1).
has a fixed point which is a solution of the problem (1.1).
In the following theorem we give an existence result for the problem (1.1) by applying the nonlinear alternative of Leray-Schauder type and by which the conditions  and
and  are weakened.
are weakened.
Theorem 3.3.
Assume that  and the following conditions hold.
and the following conditions hold.
There exists  and
and  continuous and nondecreasing such that
continuous and nondecreasing such that

There exist  continuous and nondecreasing such that
continuous and nondecreasing such that

There exists a number  such that
such that

where  .
.
Then (1.1) has at least one solution on  .
.
Proof.
Consider the operator  defined in Theorem 3.1. It can be easily shown that
defined in Theorem 3.1. It can be easily shown that  is continuous and completely continuous. For
is continuous and completely continuous. For  and each
and each  , let
, let  . Then from
. Then from  and
and  , and we have
, and we have

Thus,

Then by  , there exists
, there exists  such that
such that  . Let
. Let

The operator  is a continuous and completely continuous. From the choice of
is a continuous and completely continuous. From the choice of  , there is no
, there is no  such that
such that  for some
for some  . As a consequence of the nonlinear alternative of Leray-Schauder type, we deduce that
. As a consequence of the nonlinear alternative of Leray-Schauder type, we deduce that  has a fixed point
has a fixed point  in
in  which is a solution of the problem (1.1). This completes the proof.
which is a solution of the problem (1.1). This completes the proof.
4. Example
Let  ,
,  ,
,  . We consider the following boundary value problem:
. We consider the following boundary value problem:

where

Obviously  . Further,
. Further,

Thus, all the assumptions of Theorem 3.1 are satisfied. Hence, by the conclusion of Theorem 3.1, the impulsive fractional antiperiodic boundary value problem has a unique solution on  .
.
References
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005,311(2):495-505. 10.1016/j.jmaa.2005.02.052
Kosmatov N: A singular boundary value problem for nonlinear differential equations of fractional order. Journal of Applied Mathematics and Computing 2009,29(1-2):125-135. 10.1007/s12190-008-0104-x
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Computers & Mathematics with Applications 2010,59(3):1363-1375.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Tian Y, Chen A: The existence of positive solution to three-point singular boundary value problem of fractional differential equation. Abstract and Applied Analysis 2009, 2009:-18.
Zhang SQ: Positive solutions for boundary value problems of nonlinear fractional differential equtions. Electronic Journal of Differential Equations 2006, 2006: 1-12.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 14. World Scientific, River Edge, NJ, USA; 1995:x+462.
Lin X, Jiang D: Multiple positive solutions of Dirichlet boundary value problems for second order impulsive differential equations. Journal of Mathematical Analysis and Applications 2006,321(2):501-514. 10.1016/j.jmaa.2005.07.076
Nieto JJ, Rodríguez-López R: Boundary value problems for a class of impulsive functional equations. Computers & Mathematics with Applications 2008,55(12):2715-2731. 10.1016/j.camwa.2007.10.019
Shen J, Wang W: Impulsive boundary value problems with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):4055-4062. 10.1016/j.na.2007.10.036
Xiao J, Nieto JJ, Luo Z: Multiple positive solutions of the singular boundary value problem for second-order impulsive differential equations on the half-line. Boundary Value Problems 2010, 2010:-13.
Agarwal RP, Benchohra M, Slimani BA: Existence results for differential equations with fractional order and impulses. Memoirs on Differential Equations and Mathematical Physics 2008, 44: 1-21.
Ahmad B, Sivasundaram S: Existence results for nonlinear impulsive hybrid boundary value problems involving fractional differential equations. Nonlinear Analysis: Hybrid Systems 2009,3(3):251-258. 10.1016/j.nahs.2009.01.008
Ahmad B, Sivasundaram S: Existence of solutions for impulsive integral boundary value problems of fractional order. Nonlinear Analysis: Hybrid Systems 2010,4(1):134-141. 10.1016/j.nahs.2009.09.002
Tian Y, Bai Z: Existence results for the three-point impulsive boundary value problem involving fractional differential equations. Computers & Mathematics with Applications 2010,59(8):2601-2609. 10.1016/j.camwa.2010.01.028
Maraaba T, Baleanu D, Jarad F: Existence and uniqueness theorem for a class of delay differential equations with left and right Caputo fractional derivatives. Journal of Mathematical Physics 2008,49(8):-11.
Maraaba TA, Jarad F, Baleanu D: On the existence and the uniqueness theorem for fractional differential equations with bounded delay within Caputo derivatives. Science in China. Series A 2008,51(10):1775-1786. 10.1007/s11425-008-0068-1
Wang JR, Yang YL, Wei W: Nonlocal impulsive problems for fractional differential equations with time-varying generating operators in Banach spaces. Opuscula Mathematica 2010,30(3):361-381.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Granas A, Guenther RB, Lee JW: Some general existence principles in the Carathéodory theory of nonlinear differential systems. Journal de Mathématiques Pures et Appliquées 1991,70(2):153-196.
Schaefer H: Über die Methode der a priori-Schranken. Mathematische Annalen 1955, 129: 415-416. 10.1007/BF01362380
Acknowledgments
This work was supported by the Natural Science Foundation of China (10971173), the Natural Science Foundation of Hunan Province (10JJ3096), the Aid Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province, and the Construct Program of the Key Discipline in Hunan Province.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, A., Chen, Y. Existence of Solutions to Anti-Periodic Boundary Value Problem for Nonlinear Fractional Differential Equations with Impulses. Adv Differ Equ 2011, 915689 (2011). https://doi.org/10.1155/2011/915689
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/915689
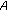 has a fixed point in
has a fixed point in 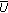 , or
, or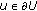 and
and  with
with 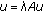 .
.