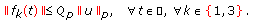- Research Article
- Open access
- Published:
Integral Equations and Exponential Trichotomy of Skew-Product Flows
Advances in Difference Equations volume 2011, Article number: 918274 (2011)
Abstract
We are interested in an open problem concerning the integral characterizations of the uniform exponential trichotomy of skew-product flows. We introduce a new admissibility concept which relies on a double solvability of an associated integral equation and prove that this provides several interesting asymptotic properties. The main results will establish the connections between this new admissibility concept and the existence of the most general case of exponential trichotomy. We obtain for the first time necessary and sufficient characterizations for the uniform exponential trichotomy of skew-product flows in infinite-dimensional spaces, using integral equations. Our techniques also provide a nice link between the asymptotic methods in the theory of difference equations, the qualitative theory of dynamical systems in continuous time, and certain related control problems.
1. Introduction
Exponential trichotomy is the most complex asymptotic property of evolution equations, being firmly rooted in bifurcation theory of dynamical systems. The concept proceeds from the central manifold theorem and mainly relies on the decomposition of the state space into a direct sum of three invariant closed subspaces: the stable subspace, the unstable subspace, and the neutral subspace such that the behavior of the solution on the stable and unstable subspaces is described by exponential decay backward and forward in time and, respectively, the solution is bounded on the neutral subspace. The concept of exponential trichotomy for differential equations has the origin in the remarkable works of Elaydi and Hájek (see [1, 2]). Elaydi and Hájek introduced the concept of exponential trichotomy for linear and nonlinear differential systems and proved a number of notable properties in these cases (see [1, 2]). These works were the starting points for the development of this subject in various directions (see [3–8], and the references therein). In [5] the author gave necessary and sufficient conditions for exponential trichotomy of difference equations by examining the existence of a bounded solution of the corresponding inhomogeneous system. Paper [4] brings a valuable contribution to the study of the exponential trichotomy. In this paper Elaydi and Janglajew obtained the first input-output characterization for exponential trichotomy (see Theorem 4, page 423). More precisely, the authors proved that a system  of difference equations with
of difference equations with  a
a  invertible matrix on
invertible matrix on  , has an (E-H)-trichotomy if and only if the associated inhomogeneous system
, has an (E-H)-trichotomy if and only if the associated inhomogeneous system  has at least one bounded solution on
has at least one bounded solution on  for every bounded input
for every bounded input  . In [4] the applicability area of exponential trichotomy was extended, by introducing new concepts of exponential dichotomy and exponential trichotomy. The authors proposed two different methods: in the first approach the authors used the tracking method and in the second approach they introduced a discrete analogue of dichotomy and trichotomy in variation.
. In [4] the applicability area of exponential trichotomy was extended, by introducing new concepts of exponential dichotomy and exponential trichotomy. The authors proposed two different methods: in the first approach the authors used the tracking method and in the second approach they introduced a discrete analogue of dichotomy and trichotomy in variation.
A new step in the study of the exponential trichotomy of difference equations was made in [3], where Cuevas and Vidal obtained the structure of the range of each trichotomy projection associated with a system of difference equations which has weighted exponential trichotomy. This approach allows them to deduce the connections between weighted exponential trichotomy and the  trichotomy on
trichotomy on  and
and  as well as to present some applications to the case of nonhomogeneous linear systems. In [8] the authors deduce the explicit formula in terms of the trichotomy projections for the solution of the nonlinear system associated with a system of difference equations which has weighted exponential trichotomy. The first study for exponential trichotomy of variational difference equations was presented in [6], the methods being provided directly for the infinite-dimensional case. There we obtained necessary and sufficient conditions for uniform exponential trichotomy of variational difference equations in terms of the solvability of an associated discrete-time control system.
as well as to present some applications to the case of nonhomogeneous linear systems. In [8] the authors deduce the explicit formula in terms of the trichotomy projections for the solution of the nonlinear system associated with a system of difference equations which has weighted exponential trichotomy. The first study for exponential trichotomy of variational difference equations was presented in [6], the methods being provided directly for the infinite-dimensional case. There we obtained necessary and sufficient conditions for uniform exponential trichotomy of variational difference equations in terms of the solvability of an associated discrete-time control system.
Starting with the ideas delineated by the pioneering work of Perron (see [9]) and developed later in remarkable works by Coppel (see [10]), Daleckii and Krein (see [11]), Massera and Schäffer (see [12]) one of the most operational tool in the study of the asymptotic behavior of an evolution equation is represented by the input-output conditions. These methods arise from control theory and often provide characterizations of the asymptotic properties of dynamical systems in terms of the solvability of some associated control systems (see [4, 6, 13–21]). According to our knowledge, in the existent literature, there are no input-output integral characterizations for uniform exponential trichotomy of skew-product flows. Moreover, the territory of integral admissibility for exponential trichotomy of skew-product flows was not explored yet. These facts led to a collection of open questions concerning this topic and, respectively, concerning the operational connotations and consequences in the framework of general variational systems.
The aim of the present paper is to present for the first time a study of exponential trichotomy of skew-product flows from the new perspective of the integral admissibility. We treat the most general case of exponential trichotomy of skew-product flows (see Definition 2.4) which is a direct generalization of the exponential dichotomy (see [13, 14, 19–22]) and is tightly related to the behavior described by the central manifold theorem. Our methods will be based on the connections between the asymptotic properties of variational difference equations, the qualitative behavior of skew-product flows, and control type techniques, providing an interesting interference between the discrete-time and the continuous-time behavior of variational systems. We also emphasize that our central purpose is to deduce a characterization for uniform exponential trichotomy without assuming a priori the existence of the projection families, without supposing the invariance with respect to the projection families or the invertibility on the unstable subspace or on the bounded subspace.
We will introduce a new concept of admissibility which relies on a double solvability of an associated integral equation and on the uniform boundedness of the norm of solution relative to the norm of the input function. Using detailed and constructive methods we will prove that this assures the existence of the uniform exponential trichotomy (with all its properties), without any additional hypothesis on the skew-product flow. Moreover, we will show that the admissibility is also a necessary condition for uniform exponential trichotomy. Thus, we deduce the premiere characterization of the uniform exponential trichotomy of skew-product flows in terms of the solvability of an associated integral equation. The results are obtained in the most general case, being applicable to any class of variational equations described by skew-product flows.
2. Basic Definitions and Preliminaries
In this section, for the sake of clarity, we will give some basic definitions and notations and we will present some auxiliary results.
Let  be a real or a complex Banach space. The norm on
be a real or a complex Banach space. The norm on  and on
and on  , the Banach algebra of all bounded linear operators on
, the Banach algebra of all bounded linear operators on  , will be denoted by
, will be denoted by  . The identity operator on
. The identity operator on  will be denoted by
will be denoted by  .
.
Throughout the paper  denotes the set of real numbers and
denotes the set of real numbers and  denotes the set of real integers. If
denotes the set of real integers. If  then we denote
then we denote  and
and  .
.
Notations
-
(i)
We consider the spaces
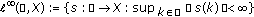 ,
, 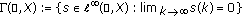 ,
, 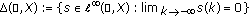 and
and 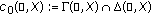 , which are Banach spaces with respect to the norm
, which are Banach spaces with respect to the norm 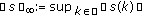 .
. -
(ii)
If
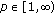 then
then 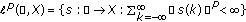 is a Banach space with respect to the norm
is a Banach space with respect to the norm 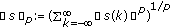 .
. -
(iii)
Let
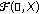 be the linear space of all
be the linear space of all 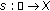 with the property that
with the property that 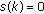 , for all
, for all 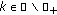 and the set
and the set  is finite.
is finite.
Let  be a metric space and let
be a metric space and let  .
.
Definition 2.1.
A continuous mapping  is called a flow on
is called a flow on  if
if  and
and  , for all
, for all  .
.
Definition 2.2.
A pair  is called (linear) skew-product flow on
is called (linear) skew-product flow on  if
if  is a flow on
is a flow on  and the mapping
and the mapping  , called cocycle, satisfies the following conditions:
, called cocycle, satisfies the following conditions:
-
(i)
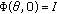 , for all
, for all  ;
; -
(ii)
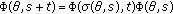 , for all
, for all 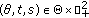 (the cocycle identity);
(the cocycle identity); -
(iii)
there are
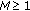 and
and 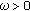 such that
such that 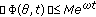 , for all
, for all 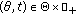 ;
; -
(iv)
for every
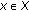 the mapping
the mapping 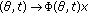 is continuous.
is continuous.
Example 2.3.
Let  be a continuous increasing function with
be a continuous increasing function with  and let
and let  . We denote by
. We denote by  the closure of
the closure of  in
in  , where
, where  denotes the space of all continuous functions
denotes the space of all continuous functions  and
and

where  .
.
Let  be a Banach space and let
be a Banach space and let  be a
be a  -semigroup on
-semigroup on  with the infinitesimal generator
with the infinitesimal generator  . For every
. For every  let
let  . We define
. We define  and we consider the system
and we consider the system

If  , then
, then  is a skew-product flow on
is a skew-product flow on  . For every
. For every  , we note that
, we note that  , for all
, for all  , is the strong solution of the system ( ).
, is the strong solution of the system ( ).
For other examples which illustrate the modeling of solutions of variational equations by means of skew-product flows as well as the existence of the perturbed skew-product flow we refer to [21] (see Examples 2.2 and 2.4). Interesting examples of skew-product flows which often proceed from the linearization of nonlinear equations can be found in [7, 13, 14, 22, 23], motivating the usual appellation of linear skew-product flows.
The most complex description of the asymptotic property of a dynamical system is given by the exponential trichotomy, which provides a complete chart of the qualitative behaviors of the solutions on each fundamental manifold: the stable manifold, the central manifold, and the unstable manifold. This means that the state space is decomposed at every point of the flow's domain—the base space—into a direct sum of three invariant closed subspaces such that the solution on the first and on the third subspace exponentially decays forward and backward in time, while on the central subspace the solution had a uniform upper and lower bound (see [1–6, 8]).
Definition 2.4.
A skew-product flow  is said to be uniformly exponentially trichotomic if there are three families of projections
is said to be uniformly exponentially trichotomic if there are three families of projections  ,
,  and two constants
and two constants  and
and  such that
such that
-
(i)
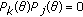 , for all
, for all 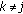 and all
and all  ,
, -
(ii)
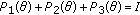 , for all
, for all 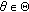 ,
, -
(iii)
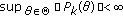 , for all
, for all 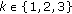 ,
, -
(iv)
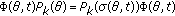 , for all
, for all 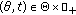 and all
and all 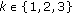 ,
, -
(v)
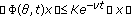 , for all
, for all 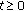 ,
, 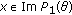 and all
and all  ,
, -
(vi)
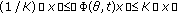 , for all
, for all  ,
,  and all
and all 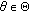 ,
, -
(vii)
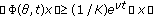 , for all
, for all  ,
, 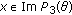 and all
and all  ,
, -
(viii)
the restriction
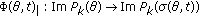 is an isomorphism, for all
is an isomorphism, for all 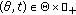 and all
and all 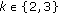 .
.
Remark 2.5.
We note that this is a direct generalization of the classical concept of uniform exponential dichotomy (see [13, 14, 19–22, 24, 25]) and expresses the behavior described by the central manifold theorem. It is easily seen that for  , for all
, for all  , one obtains the uniform exponential dichotomy concept and the condition (iii) is redundant (see, e.g., [19, Lemma 2.8]).
, one obtains the uniform exponential dichotomy concept and the condition (iii) is redundant (see, e.g., [19, Lemma 2.8]).
Remark 2.6.
If a skew-product flow is uniformly exponentially trichotomic with respect to the families of projections  ,
,  , then
, then
-
(i)
 , for all
, for all  ;
; -
(ii)
 , for all
, for all  and all
and all 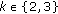 .
.
Let  be a skew-product flow on
be a skew-product flow on  . At every point
. At every point  we associate with
we associate with  three fundamental subspaces, which will have a crucial role in the study of the uniform exponential trichotomy.
three fundamental subspaces, which will have a crucial role in the study of the uniform exponential trichotomy.
Notation
For every  we denote by
we denote by  the linear space of all functions
the linear space of all functions  with
with

For every  we consider the linear space:
we consider the linear space:

called the stable subspace. We also define

called the bounded subspace and, respectively,

called the unstable subspace.
Lemma 2.7.
-
(i)
If for every
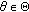 ,
, 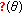 denotes one of the subspaces
denotes one of the subspaces 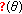 ,
,  or
or 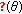 , then
, then 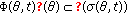 , for all
, for all 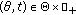 .
. -
(ii)
If the skew-product flow
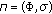 is uniformly exponentially trichotomic with respect to three families of projections
is uniformly exponentially trichotomic with respect to three families of projections  ,
, 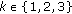 , then these families are uniquely determined by the conditions in Definition 2.4. Moreover one has that
, then these families are uniquely determined by the conditions in Definition 2.4. Moreover one has that  (2.6)
(2.6)
Proof.
See [6, Lemma 5.4, Proposition 5.5, and Remark 5.3].
We will start our investigation by recalling a recent result obtained for the discrete-time case. Precisely, the discrete case was treated in [6], where we formulated a first resolution concerning the characterization of the uniform exponential trichotomy in terms of the solvability of a system of variational difference equations. Indeed, we associated with the skew-product flow  the discrete input-output system
the discrete input-output system  , where for every
, where for every 

with  and
and  .
.
Definition 2.8.
The pair  is said to be uniformly admissible for the skew-product flow
is said to be uniformly admissible for the skew-product flow  if there are
if there are  and
and  such that for every
such that for every  the following properties hold:
the following properties hold:
-
(i)
for every
 there are
there are 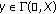 and
and 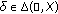 such that the pairs
such that the pairs 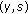 and
and 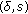 satisfy ( );
satisfy ( ); -
(ii)
if
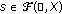 and
and 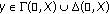 is such that the pair
is such that the pair 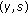 satisfies ( ) then
satisfies ( ) then 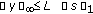 ;
; -
(iii)
if
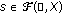 is such that
is such that 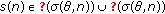 , for all
, for all 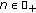 , and
, and 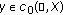 is such that the pair
is such that the pair  satisfies ( ), then
satisfies ( ), then 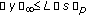 .
.
The first connection between an input-output discrete admissibility and the uniform exponential trichotomy of skew-product flows was obtained in [6] (see Theorem 5.8) and this is given by what follows.
Theorem 2.9.
Let  be a skew-product flow on
be a skew-product flow on  .
.  is uniformly exponentially trichotomic if and only if the pair
is uniformly exponentially trichotomic if and only if the pair  is uniformly admissible for
is uniformly admissible for  .
.
The proof of this result relies completely on discrete-time arguments and essentially uses the properties of the associated system of variational difference equations. The natural question is whether we may study the uniform exponential trichotomy property of skew-product flows from a "continuous" point of view. On the other hand, in the spirit of the classical admissibility theory (see [10–12, 14, 15, 21]) it would be interesting to see if the uniform exponential trichotomy can be expressed in terms of the solvability of an integral equation. The aim of the next section will be to give a complete resolution to these questions. Thus, we are interested in solving for the first time the problem of characterizing the exponential trichotomy of skew-product flows in terms of the solvability of an integral equation and also in establishing the connections between the qualitative theory of difference equations and the continuous-time behavior of dynamical systems, pointing out how the discrete-time arguments provide interesting information in control problems related with the existence of the exponential trichotomy.
3. Main Results
Let  be a real or a complex Banach space. In this section, we will present a complete study concerning the characterization of uniform exponential trichotomy using a special solvability of an associated integral equation. We introduce a new and natural admissibility concept and we show that the trichotomic behavior of skew-product flows can be studied in the most general case, without any additional assumptions.
be a real or a complex Banach space. In this section, we will present a complete study concerning the characterization of uniform exponential trichotomy using a special solvability of an associated integral equation. We introduce a new and natural admissibility concept and we show that the trichotomic behavior of skew-product flows can be studied in the most general case, without any additional assumptions.
Notations
Let  , which is a Banach space with respect to the norm
, which is a Banach space with respect to the norm  . We consider the spaces
. We consider the spaces  ,
,  and let
and let  . Then
. Then  and
and  are closed linear subspaces of
are closed linear subspaces of  . Let
. Let  be the space of all continuous functions
be the space of all continuous functions  with compact support and
with compact support and  .
.
Let  and let
and let  be the linear space of all Bochner measurable functions
be the linear space of all Bochner measurable functions  with the property that
with the property that  , which is a Banach space with respect to the norm
, which is a Banach space with respect to the norm

Let  be a metric space and let
be a metric space and let  be a skew-product flow. For every
be a skew-product flow. For every  we consider the integral equation
we consider the integral equation

with  and
and  .
.
Definition 3.1.
The pair  is said to beuniformly admissible for the skew-product flow
is said to beuniformly admissible for the skew-product flow  if there are
if there are  and
and  such that for every
such that for every  the following properties hold:
the following properties hold:
-
(i)
for every
 there are
there are 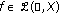 and
and 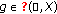 such that the pairs
such that the pairs  and
and 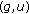 satisfy ( );
satisfy ( ); -
(ii)
if
 and
and 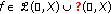 are such that the pair
are such that the pair 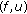 satisfies ( ), then
satisfies ( ), then 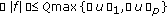 ;
; -
(iii)
if
 is such that
is such that 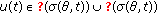 , for all
, for all  and
and 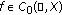 has the property that the pair
has the property that the pair 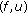 satisfies ( ), then
satisfies ( ), then 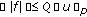 .
.
Remark 3.2.
In the above admissibility concept, the input space is a minimal one, because all the test functions  belong to the space
belong to the space  .
.
In what follows we will establish the connections between the admissibility and the existence of uniform exponential trichotomy.
The first main result of this paper is as follows.
Theorem 3.3.
Let  be a skew-product flow on
be a skew-product flow on  . If the pair
. If the pair  ,
,  is uniformly admissible for
is uniformly admissible for  , then
, then  is uniformly exponentially trichotomic.
is uniformly exponentially trichotomic.
Proof.
We prove that the pair  is uniformly admissible for
is uniformly admissible for  .
.
Indeed, let  and
and  be given by Definition 3.1. We consider a continuous function
be given by Definition 3.1. We consider a continuous function  with the support contained in
with the support contained in  and
and

Let  be such that
be such that  , for all
, for all  . Since
. Since  there is
there is  such that
such that



Let  .
.
Step 1.
Let  . We consider the function
. We consider the function

Then  is continuous and
is continuous and

Since  there is
there is  such that
such that  . Then, from (3.7) it follows that
. Then, from (3.7) it follows that  , so
, so  . According to our hypothesis it follows that there are
. According to our hypothesis it follows that there are  and
and  such that the pairs
such that the pairs  and
and  satisfy ( ).
satisfy ( ).
Then, for every  we obtain that
we obtain that

Let

From (3.8) we have that

so the pair  satisfies ( ). Moreover, since
satisfies ( ). Moreover, since  and
and  , we deduce that
, we deduce that  . Since the pair
. Since the pair  satisfies ( ) we obtain that
satisfies ( ) we obtain that

Taking

we analogously obtain that  and the pair
and the pair  satisfies ( ).
satisfies ( ).
Step 2.
Let  and let
and let  be such that the pair
be such that the pair  satisfies ( ). We consider the functions
satisfies ( ). We consider the functions  , given by
, given by

Since  we have that
we have that  . Observing that for every
. Observing that for every 

we deduce that  is continuous. Moreover, since
is continuous. Moreover, since  and
and  , from
, from

we obtain that  .
.
Let  . We prove that
. We prove that

We set  . If
. If  , then, taking into account the way how
, then, taking into account the way how  was defined, the relation (3.16) obviously holds. If
was defined, the relation (3.16) obviously holds. If  then there is
then there is  ,
,  such that
such that  . Then, we deduce that
. Then, we deduce that

If  then
then  and
and

If  then
then

From relations (3.18) and (3.19) we have that

Then, from (3.17) and (3.20) it follows that

Since the pair  satisfies ( ) we have that
satisfies ( ) we have that

From (3.21) and (3.22) we obtain that the relation (3.16) holds for all  . Since
. Since  was arbitrary we deduce that the pair
was arbitrary we deduce that the pair  satisfies ( ). Then according to our hypothesis we have that
satisfies ( ). Then according to our hypothesis we have that

In addition, we have that

and that

Taking  , from relations (3.23)–(3.25) and (3.3) it follows that
, from relations (3.23)–(3.25) and (3.3) it follows that

Observing that  , for all
, for all  , from (3.26) and (3.4) we successively deduce that
, from (3.26) and (3.4) we successively deduce that

Setting  , from relation (3.27) we deduce that
, from relation (3.27) we deduce that

Step 3.
Let  be such that
be such that  , for all
, for all  and let
and let  be such that the pair
be such that the pair  satisfies ( ). We consider the functions
satisfies ( ). We consider the functions  , given by
, given by

Using analogous arguments with those used in the Step 2 we obtain that  and the pair
and the pair  satisfies ( ). Moreover, using Lemma 2.7 we have that
satisfies ( ). Moreover, using Lemma 2.7 we have that  , for all
, for all  . Then, according to our hypothesis we deduce that
. Then, according to our hypothesis we deduce that

Since  , for all
, for all  , using (3.30) and (3.5) we obtain that
, using (3.30) and (3.5) we obtain that

Observing that

from (3.31) and (3.32) we deduce that

where  .
.
Finally, from Steps 1–3 and relations (3.28) and (3.33) we deduce that the pair  is uniformly admissible for the skew-product flow
is uniformly admissible for the skew-product flow  . By applying Theorem 2.9 we conclude that
. By applying Theorem 2.9 we conclude that  is uniformly exponentially trichotomic.
is uniformly exponentially trichotomic.
The natural question arises whether the integral admissibility given by Definition 3.1 is also a necessary condition for the existence of the uniform exponential trichotomy. To answer this question, in what follows, our attention will focus on the converse implication of the result given by Theorem 3.3. Specifically, our study will motivate the admissibility concept introduced in this paper and will point out several qualitative aspects. First of all, we prove a technical result.
Proposition 3.4.
Let  be a skew-product flow which is uniformly exponentially trichotomic with respect to the families of projections
be a skew-product flow which is uniformly exponentially trichotomic with respect to the families of projections  . Let
. Let  , let
, let  , and let
, and let  be such that the pair
be such that the pair  satisfies ( ). We denote
satisfies ( ). We denote

and let  denote the inverse of the operator
denote the inverse of the operator 
 , for all
, for all  . The following assertions hold:
. The following assertions hold:
-
(i)
the functions
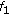 and
and 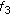 have the following representations
have the following representations 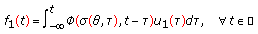 (3.35)
(3.35) (3.36)
(3.36) -
(ii)
for every
 there is
there is  which does not depend on
which does not depend on 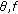 or
or  such that
such that (3.37)
(3.37)
Proof.
Since  there is
there is  such that
such that  . Let
. Let  be given by Definition 2.4 and let
be given by Definition 2.4 and let  .
.
-
(i)
Since the pair
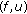 satisfies ( ) we have that
satisfies ( ) we have that  (3.38)
(3.38)
Since  from (3.38) we have that
from (3.38) we have that  , for all
, for all  . Let
. Let  . Then we deduce that
. Then we deduce that

For  in (3.39) we obtain that
in (3.39) we obtain that  , for all
, for all  . This shows that relation (3.35) holds for all
. This shows that relation (3.35) holds for all  . For
. For  from (3.38) we have that
from (3.38) we have that

so relation (3.35) holds for every  .
.
For every  from (3.38) we have that
from (3.38) we have that  . This implies that
. This implies that

so we deduce that

From relation (3.42) it follows that  , for all
, for all  . In particular, we have that relation (3.36) holds for
. In particular, we have that relation (3.36) holds for  . For
. For  from (3.38) we obtain that
from (3.38) we obtain that

which implies that

for all  . Thus, we conclude that relation (3.36) holds for every
. Thus, we conclude that relation (3.36) holds for every  .
.
-
(ii)
Let
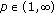 and let
and let 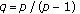 . Setting
. Setting 
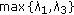 and using Hölder's inequality we deduce that
and using Hölder's inequality we deduce that 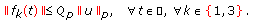 (3.45)
(3.45)
The second main result of the paper is as follows.
Theorem 3.5.
Let  be a skew-product flow. If
be a skew-product flow. If  is uniformly exponentially trichotomic, then the pair
is uniformly exponentially trichotomic, then the pair  ,
, is uniformly admissible for
is uniformly admissible for  .
.
Proof.
Let  be two constants and let
be two constants and let  ,
,  be the families of projections given by Definition 2.4. We set
be the families of projections given by Definition 2.4. We set  . For every
. For every  and every
and every  we denote by
we denote by  the inverse of the operator
the inverse of the operator  .
.
For every  and every
and every  we denote by
we denote by

Then  , for all
, for all  and all
and all  and
and  , for all
, for all  .
.
Let  and let
and let  be given by Proposition 3.4. We prove that all the properties from Definition 3.1 are fulfilled.
be given by Proposition 3.4. We prove that all the properties from Definition 3.1 are fulfilled.
Let  .
.
Step 1.
Let  ,
,  . We consider the functions
. We consider the functions  defined by
defined by

Since  we have that
we have that  and
and  are correctly defined and continuous. Let
are correctly defined and continuous. Let  be such that
be such that  . Setting
. Setting  ,
,  and
and  , we have that
, we have that  and
and  , for
, for  .
.
We observe that  , for all
, for all  , which implies that
, which implies that

In addition, we have that  , for all
, for all  . This implies that
. This implies that

Since  is continuous from relations (3.48) and (3.49) it follows that
is continuous from relations (3.48) and (3.49) it follows that  . Using similar arguments we deduce that
. Using similar arguments we deduce that  . An easy computation shows that the pairs
. An easy computation shows that the pairs  and
and  satisfy ( ).
satisfy ( ).
If  , then we take
, then we take  .
.
Step 2.
Let  and let
and let  be such that the pair
be such that the pair  satisfies ( ).
satisfies ( ).
Suppose that  . From Proposition 3.4 we have that
. From Proposition 3.4 we have that

Let  be such that
be such that  . Since
. Since

for  we deduce that
we deduce that  . Since
. Since  we obtain that
we obtain that

so  . This implies that
. This implies that  , for all
, for all  . Moreover, using (3.51), for
. Moreover, using (3.51), for  we have that
we have that

which implies that

Then, we obtain that

Setting  from relations (3.50) and (3.55) it follows that
from relations (3.50) and (3.55) it follows that

The case  can be treated using similar arguments with those used above.
can be treated using similar arguments with those used above.
Step 3.
Let  be such that
be such that  , for all
, for all  and let
and let  be such that the pair
be such that the pair  satisfies ( ).
satisfies ( ).
Since  and
and  , for all
, for all  , using Lemma 2.7 we deduce that
, using Lemma 2.7 we deduce that  , for all
, for all  . Since the pair
. Since the pair  satisfies ( ) we obtain that
satisfies ( ) we obtain that

Let  . Since
. Since  , using relation (3.57) we have that
, using relation (3.57) we have that

so  , for all
, for all  . This shows that, in this case,
. This shows that, in this case,  .
.
If  is given by Step 2, we deduce that
is given by Step 2, we deduce that

and the proof is complete.
The central result of this paper is as follows.
Theorem 3.6.
A skew-product flow  is uniformly exponentially trichotomic if and only if the pair
is uniformly exponentially trichotomic if and only if the pair  is uniformly admissible for
is uniformly admissible for  .
.
Proof.
This follows from Theorems 3.3 and 3.5.
Remark 3.7.
The above result establishes for the first time in the literature a necessary and sufficient condition for the existence of the uniform exponential trichotomy of skew-product flows, based on an input-output admissibility with respect to the associated integral equation. The chart described by our method allows a direct analysis of the asymptotic behavior of skew-product flows, without assuming a priori the existence of a projection families, invariance properties or any reversibility properties. Moreover, the study is done in the most general case, without any additional assumptions concerning the flow or the cocycle.
References
Elaydi S, Hájek O: Exponential trichotomy of differential systems. Journal of Mathematical Analysis and Applications 1988,129(2):362-374. 10.1016/0022-247X(88)90255-7
Elaydi S, Hájek O: Exponential dichotomy and trichotomy of nonlinear differential equations. Differential and Integral Equations 1990,3(6):1201-1224.
Cuevas C, Vidal C: Weighted exponential trichotomy of linear difference equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(3):353-379.
Elaydi S, Janglajew K: Dichotomy and trichotomy of difference equations. Journal of Difference Equations and Applications 1998,3(5-6):417-448.
Papaschinopoulos G: On exponential trichotomy of linear difference equations. Applicable Analysis 1991,40(2-3):89-109. 10.1080/00036819108839996
Sasu AL, Sasu B: Exponential trichotomy for variational difference equations. Journal of Difference Equations and Applications 2009,15(7):693-718. 10.1080/10236190802285118
Wang B-G, Li W-T: Limit set trichotomy and dichotomy for skew-product semiflows with applications. Nonlinear Analysis 2009, 71: 2834-2839. 10.1016/j.na.2009.01.135
Vidal C, Cuevas C, del Campo L: Weighted exponential trichotomy of difference equations. In Dynamic Systems and Applications. Vol. 5. Dynamic, Atlanta, Ga, USA; 2008:489-495.
Perron O: Die Stabilitätsfrage bei Differentialgleichungen. Mathematische Zeitschrift 1930,32(1):703-728. 10.1007/BF01194662
Coppel WA: Dichotomies in Stability Theory, Lecture Notes in Mathematics. Volume 629. Springer, Berlin, Germany; 1978:ii+98.
Daleckii JL, Krein MG: Stability of Solutions of Differential Equations in Banach Space, Translations of Mathematical Monographs. Volume 43. American Mathematical Society, Providence, RI, USA; 1974:vi+386.
Massera JL, Schäffer JJ: Linear Differential Equations and Function Spaces, Pure and Applied Mathematics. Volume 21. Academic Press, New York, NY, USA; 1966:xx+404.
Chow S-N, Leiva H: Existence and roughness of the exponential dichotomy for skew-product semiflow in Banach spaces. Journal of Differential Equations 1995,120(2):429-477. 10.1006/jdeq.1995.1117
Megan M, Sasu AL, Sasu B: Perron conditions for pointwise and global exponential dichotomy of linear skew-product flows. Integral Equations and Operator Theory 2004,50(4):489-504. 10.1007/s00020-003-1234-z
Van Minh N, Räbiger F, Schnaubelt R: Exponential stability, exponential expansiveness, and exponential dichotomy of evolution equations on the half-line. Integral Equations and Operator Theory 1998,32(3):332-353. 10.1007/BF01203774
Minh NV, N'Guérékata GM, Yuan R: Lectures on the Asymptotic Behavior of Solutions of Differential Equations. Nova Science, New York, NY, USA; 2008:viii+65.
Sasu B: New criteria for exponential expansiveness of variational difference equations. Journal of Mathematical Analysis and Applications 2007,327(1):287-297. 10.1016/j.jmaa.2006.04.024
Sasu B: Robust stability and stability radius for variational control systems. Abstract and Applied Analysis 2008, 2008:-29.
Sasu B: On dichotomous behavior of variational difference equations and applications. Discrete Dynamics in Nature and Society 2009, 2009:-16.
Sasu B: Input-output control systems and dichotomy of variational difference equations. Journal of Difference Equations and Applications. In press
Sasu AL, Sasu B: Integral equations in the study of the asymptotic behavior of skew-product flows. Asymptotic Analysis 2010,68(3):135-153.
Chow S-N, Leiva H: Unbounded perturbation of the exponential dichotomy for evolution equations. Journal of Differential Equations 1996,129(2):509-531. 10.1006/jdeq.1996.0125
Foiaş C, Sell GR, Temam R: Inertial manifolds for nonlinear evolutionary equations. Journal of Differential Equations 1988,73(2):309-353. 10.1016/0022-0396(88)90110-6
Diagana T: Existence of pseudo-almost automorphic mild solutions to some nonautonomous partial evolution equations. Advances in Difference Equations 2011, 2011:-23.
Diagana T: Existence of weighted pseudo-almost periodic solutions to some classes of nonautonomous partial evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2011,74(2):600-615. 10.1016/j.na.2010.09.015
Acknowledgments
The first author is supported by CNCSIS-UEFISCDI, project PN II-IDEI code 1081/2008 no. 550/2009 and the second author is supported by CNCSIS-UEFISCDI, project PN II-IDEI code 1080/2008 no. 508/2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sasu, A.L., Sasu, B. Integral Equations and Exponential Trichotomy of Skew-Product Flows. Adv Differ Equ 2011, 918274 (2011). https://doi.org/10.1155/2011/918274
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/918274
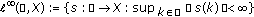 ,
, 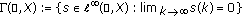 ,
, 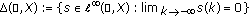 and
and 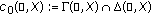 , which are Banach spaces with respect to the norm
, which are Banach spaces with respect to the norm 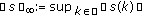 .
.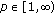 then
then 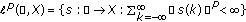 is a Banach space with respect to the norm
is a Banach space with respect to the norm 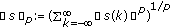 .
. be the linear space of all
be the linear space of all 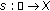 with the property that
with the property that 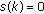 , for all
, for all 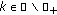 and the set
and the set  is finite.
is finite.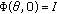 , for all
, for all  ;
;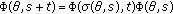 , for all
, for all 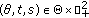 (the cocycle identity);
(the cocycle identity);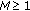 and
and 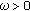 such that
such that 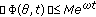 , for all
, for all 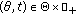 ;
;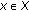 the mapping
the mapping 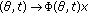 is continuous.
is continuous.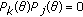 , for all
, for all 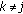 and all
and all  ,
,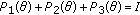 , for all
, for all 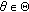 ,
,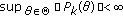 , for all
, for all 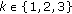 ,
,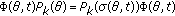 , for all
, for all 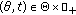 and all
and all 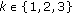 ,
,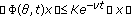 , for all
, for all 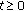 ,
, 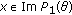 and all
and all  ,
,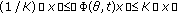 , for all
, for all  ,
,  and all
and all 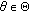 ,
,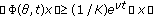 , for all
, for all  ,
, 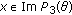 and all
and all  ,
,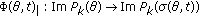 is an isomorphism, for all
is an isomorphism, for all 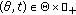 and all
and all 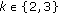 .
. , for all
, for all  ;
; , for all
, for all  and all
and all 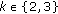 .
.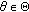 ,
, 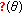 denotes one of the subspaces
denotes one of the subspaces 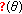 ,
,  or
or 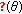 , then
, then 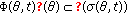 , for all
, for all 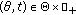 .
.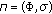 is uniformly exponentially trichotomic with respect to three families of projections
is uniformly exponentially trichotomic with respect to three families of projections  ,
, 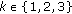 , then these families are uniquely determined by the conditions in Definition 2.4. Moreover one has that
, then these families are uniquely determined by the conditions in Definition 2.4. Moreover one has that 
 there are
there are 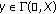 and
and 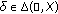 such that the pairs
such that the pairs 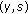 and
and 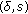 satisfy ( );
satisfy ( );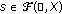 and
and 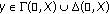 is such that the pair
is such that the pair 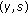 satisfies ( ) then
satisfies ( ) then 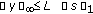 ;
;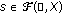 is such that
is such that 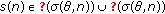 , for all
, for all 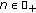 , and
, and 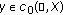 is such that the pair
is such that the pair  satisfies ( ), then
satisfies ( ), then 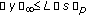 .
. there are
there are 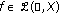 and
and 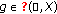 such that the pairs
such that the pairs  and
and 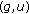 satisfy ( );
satisfy ( ); and
and 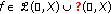 are such that the pair
are such that the pair 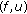 satisfies ( ), then
satisfies ( ), then 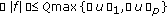 ;
; is such that
is such that 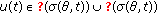 , for all
, for all  and
and 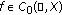 has the property that the pair
has the property that the pair 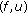 satisfies ( ), then
satisfies ( ), then 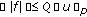 .
.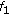 and
and 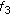 have the following representations
have the following representations 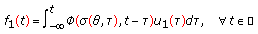

 there is
there is  which does not depend on
which does not depend on 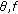 or
or  such that
such that
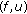 satisfies ( ) we have that
satisfies ( ) we have that 
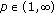 and let
and let 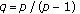 . Setting
. Setting 
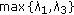 and using Hölder's inequality we deduce that
and using Hölder's inequality we deduce that