- Research Article
- Open access
- Published:
Existence of Mild Solutions to Fractional Integrodifferential Equations of Neutral Type with Infinite Delay
Advances in Difference Equations volume 2011, Article number: 963463 (2011)
Abstract
We study the solvability of the fractional integrodifferential equations of neutral type with infinite delay in a Banach space  . An existence result of mild solutions to such problems is obtained under the conditions in respect of Kuratowski's measure of noncompactness. As an application of the abstract result, we show the existence of solutions for an integrodifferential equation.
. An existence result of mild solutions to such problems is obtained under the conditions in respect of Kuratowski's measure of noncompactness. As an application of the abstract result, we show the existence of solutions for an integrodifferential equation.
1. Introduction
The fractional differential equations are valuable tools in the modeling of many phenomena in various fields of science and engineering; so, they attracted many researchers (cf., e.g., [1–6] and references therein). On the other hand, the integrodifferential equations arise in various applications such as viscoelasticity, heat equations, and many other physical phenomena (cf., e.g., [7–10] and references therein). Moreover, the Cauchy problem for various delay equations in Banach spaces has been receiving more and more attention during the past decades (cf., e.g., [7, 10–15] and references therein).
Neutral functional differential equations arise in many areas of applied mathematics and for this reason, the study of this type of equations has received great attention in the last few years (cf., e.g., [12, 14–16] and references therein). In [12, 16], Hernández and Henríquez studied neutral functional differential equations with infinite delay. In the following, we will extend such results to fractional-order functional differential equations of neutral type with infinite delay. To the authors' knowledge, few papers can be found in the literature for the solvability of the fractional-order functional integrodifferential equations of neutral type with infinite delay.
In the present paper, we will consider the following fractional integrodifferential equation of neutral type with infinite delay in Banach space  :
:

where  ,
,  ,
,  is a phase space that will be defined later (see Definition 2.5).
is a phase space that will be defined later (see Definition 2.5).  is a generator of an analytic semigroup
is a generator of an analytic semigroup  of uniformly bounded linear operators on
of uniformly bounded linear operators on  . Then, there exists
. Then, there exists  such that
such that  .
.  ,
,  ,
,  (
( ), and
), and  defined by
defined by  , for
, for  ,
,  belongs to
belongs to  and
and  . The fractional derivative is understood here in the Caputo sense.
. The fractional derivative is understood here in the Caputo sense.
The aim of our paper is to study the solvability of (1.1) and present the existence of mild solution of (1.1) based on Kuratowski's measures of noncompactness. Moreover, an example is presented to show an application of the abstract results.
2. Preliminaries
Throughout this paper, we set  and denote by
and denote by  a real Banach space, by
a real Banach space, by  the Banach space of all linear and bounded operators on
the Banach space of all linear and bounded operators on  , and by
, and by  the Banach space of all
the Banach space of all  -valued continuous functions on
-valued continuous functions on  with the uniform norm topology.
with the uniform norm topology.
Let us recall the definition of Kuratowski's measure of noncompactness.
Definition 2.1.
Let  be a bounded subset of a seminormed linear space
be a bounded subset of a seminormed linear space  . Kuratowski's measure of noncompactness of
. Kuratowski's measure of noncompactness of  is defined as
is defined as

This measure of noncompactness satisfies some important properties.
Lemma 2.2 (see [17]).
Let  and
and  be bounded subsets of
be bounded subsets of  . Then,
. Then,
-
(1)
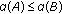 if
if 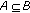 ,
, -
(2)
 , where
, where 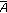 denotes the closure of
denotes the closure of 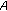 ,
, -
(3)
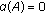 if and only if
if and only if 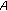 is precompact,
is precompact, -
(4)
 ,
, 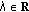 ,
, -
(5)
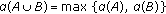 ,
, -
(6)
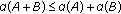 , where
, where  ,
, -
(7)
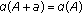 for any
for any 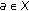 ,
, -
(8)
 , where
, where 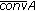 is the closed convex hull of
is the closed convex hull of 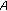 .
.
For  , we define
, we define

where  .
.
The following lemmas will be needed.
Lemma 2.3 (see [17]).
If  is a bounded, equicontinuous set, then
is a bounded, equicontinuous set, then

Lemma 2.4 (see [18]).
If  and there exists an
and there exists an  such that
such that  , a.e.
, a.e.  , then
, then  is integrable and
is integrable and

The following definition about the phase space is due to Hale and Kato [11].
Definition 2.5.
A linear space  consisting of functions from
consisting of functions from  into
into  with semi-norm
with semi-norm  is called an admissible phase space if
is called an admissible phase space if  has the following properties.
has the following properties.
-
(1)
If
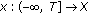 is continuous on
is continuous on 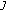 and
and 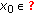 , then
, then  and
and 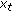 is continuous in
is continuous in 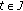 and
and (2.5)
(2.5)where
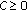 is a constant.
is a constant. -
(2)
There exist a continuous function
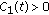 and a locally bounded function
and a locally bounded function 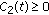 in
in 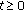 such that
such that (2.6)
(2.6)for
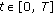 and
and  as in (1).
as in (1). -
(3)
The space
 is complete.
is complete.
Remark 2.6.
(2.5) in (1) is equivalent to  , for all
, for all  .
.
The following result will be used later.
Let  be a bounded, closed, and convex subset of a Banach space
be a bounded, closed, and convex subset of a Banach space  such that
such that  , and let
, and let  be a continuous mapping of
be a continuous mapping of  into itself. If the implication
into itself. If the implication

holds for every subset  of
of  , then
, then  has a fixed point.
has a fixed point.
Let  be a set defined by
be a set defined by

Motivated by [4, 5, 21], we give the following definition of mild solution of (1.1).
Definition 2.8.
A function  satisfying the equation
satisfying the equation

is called a mild solution of (1.1), where

and  is a probability density function defined on
is a probability density function defined on  such that
such that

where

Remark 2.9.
According to [22], direct calculation gives that

where  .
.
We list the following basic assumptions of this paper.
(H1) satisfies
satisfies  is measurable, for all
is measurable, for all  and
and  is continuous for a.e.
is continuous for a.e.  , and there exist two positive functions
, and there exist two positive functions  such that
such that

(H2) For any bounded sets  ,
,  , and
, and  , there exists an integrable positive function
, there exists an integrable positive function  such that
such that

where  and
and  .
.
(H3) There exists a constant  such that
such that

(H4) For each  ,
,  is measurable on
is measurable on  and
and  is bounded on
is bounded on  . The map
. The map  is continuous from
is continuous from  to
to  , here,
, here,  .
.
(H5) There exists  such that
such that

where  ,
,  .
.
3. Main Result
In this section, we will apply Lemma 2.7 to show the existence of mild solution of (1.1). To this end, we consider the operator  defined by
defined by

It follows from (H1), (H3), and (H4) that  is well defined.
is well defined.
It will be shown that  has a fixed point, and this fixed point is then a mild solution of (1.1).
has a fixed point, and this fixed point is then a mild solution of (1.1).
Let  be the function defined by
be the function defined by

Set  ,
,  .
.
It is clear to see that  satisfies (2.9) if and only if
satisfies (2.9) if and only if  satisfies
satisfies  and for
and for  ,
,

Let  . For any
. For any  ,
,

Thus,  is a Banach space. Set
is a Banach space. Set

Then, for  , from(2.6), we have
, from(2.6), we have

where  .
.
In order to apply Lemma 2.7 to show that  has a fixed point, we let
has a fixed point, we let  be an operator defined by
be an operator defined by  and for
and for  ,
,

Clearly, the operator  has a fixed point is equivalent to
has a fixed point is equivalent to  has one. So, it turns out to prove that
has one. So, it turns out to prove that  has a fixed point.
has a fixed point.
Now, we present and prove our main result.
Theorem 3.1.
Assume that (H1)–(H5) are satisfied, then there exists a mild solution of (1.1) on  provided that
provided that  .
.
Proof.
For  ,
,  , from (3.6), we have
, from (3.6), we have

In view of (H3),

where  .
.
Next, we show that there exists some  such that
such that  . If this is not true, then for each positive number
. If this is not true, then for each positive number  , there exist a function
, there exist a function  and some
and some  such that
such that  . However, on the other hand, we have from (3.8), (3.9), and (H4)
. However, on the other hand, we have from (3.8), (3.9), and (H4)

Dividing both sides of (3.10) by  , and taking
, and taking  , we have
, we have

This contradicts (2.17). Hence, for some positive number  ,
,  .
.
Let  with
with  in
in  as
as  . Since
. Since  satisfies (H1), for almost every
satisfies (H1), for almost every  , we get
, we get

In view of (3.6), we have

Noting that

we have by the Lebesgue Dominated Convergence Theorem that

Therefore, we obtain

This shows that  is continuous.
is continuous.
Set

Let  and
and  , then we can see
, then we can see

where

It follows the continuity of  in the uniform operator topology for
in the uniform operator topology for  that
that  tends to 0, as
tends to 0, as  . The continuity of
. The continuity of  ensures that
ensures that  tends to 0, as
tends to 0, as  .
.
For  , we have
, we have

Clearly, the first term on the right-hand side of (3.20) tends to 0 as  . The second term on the right-hand side of (3.20) tends to 0 as
. The second term on the right-hand side of (3.20) tends to 0 as  as a consequence of the continuity of
as a consequence of the continuity of  in the uniform operator topology for
in the uniform operator topology for  .
.
In view of the assumption of  and (3.8), we see that
and (3.8), we see that

Thus,  is equicontinuous.
is equicontinuous.
Now, let  be an arbitrary subset of
be an arbitrary subset of  such that
such that  .
.
Set  ,
,

Noting that for  , we have
, we have

Thus,

where  . Therefore,
. Therefore,  .
.
Moreover, for any  and bounded set
and bounded set  , we can take a sequence
, we can take a sequence  such that
such that  (see [23], P125). Thus, for
(see [23], P125). Thus, for  , noting that the choice of
, noting that the choice of  , and from Lemmas 2.2–2.4 and (H2), we have
, and from Lemmas 2.2–2.4 and (H2), we have

It follows from Lemma 2.2 that

since  is arbitrary, we can obtain
is arbitrary, we can obtain

Hence,  . Applying now Lemma 2.7, we conclude that
. Applying now Lemma 2.7, we conclude that  has a fixed point
has a fixed point  in
in  . Let
. Let  , then
, then  is a fixed point of the operator
is a fixed point of the operator  which is a mild solution of (1.1).
which is a mild solution of (1.1).
4. Application
In this section, we consider the following integrodifferential model:

where  ,
,  ,
,  ,
,  ,
,  are continuous functions, and
are continuous functions, and  .
.
Set  and define
and define  by
by

Then,  generates a compact, analytic semigroup
generates a compact, analytic semigroup  of uniformly bounded, linear operators, and
of uniformly bounded, linear operators, and  .
.
Let the phase space  be
be  , the space of bounded uniformly continuous functions endowed with the following norm:
, the space of bounded uniformly continuous functions endowed with the following norm:

then we can see that  in (2.6).
in (2.6).
For  ,
,  and
and  , we set
, we set

Then (4.1) can be reformulated as the abstract (1.1).
Moreover, for  , we can see
, we can see

where  ,
,  .
.
For  ,
,  , we have
, we have

where  .
.
Suppose further that there exists a constant  such that
such that

then (4.1) has a mild solution by Theorem 3.1.
For example, if we put

then  ,
,  ,
,  . Thus, we see
. Thus, we see

References
Agarwal RP, de Andrade B, Cuevas C: On type of periodicity and ergodicity to a class of fractional order differential equations. Advances in Difference Equations 2010, 2010:-25.
Ahmed HM: Boundary controllability of nonlinear fractional integrodifferential systems. Advances in Difference Equations 2010, 2010:-9.
Alsaedi A, Ahmad B: Existence of solutions for nonlinear fractional integro-differential equations with three-point nonlocal fractional boundary conditions. Advances in Difference Equations 2010, 2010:-10.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons and Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: On some stochastic fractional integro-differential equations. Advances in Dynamical Systems and Applications 2006,1(1):49-57.
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Liang J, Xiao T-J, van Casteren J: A note on semilinear abstract functional differential and integrodifferential equations with infinite delay. Applied Mathematics Letters 2004,17(4):473-477. 10.1016/S0893-9659(04)90092-4
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Xiao T-J, Liang J: Blow-up and global existence of solutions to integral equations with infinite delay in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e1442-e1447. 10.1016/j.na.2009.01.204
Hale JK, Kato J: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 1978,21(1):11-41.
Hernández E, Henríquez HR: Existence results for partial neutral functional-differential equations with unbounded delay. Journal of Mathematical Analysis and Applications 1998,221(2):452-475. 10.1006/jmaa.1997.5875
Liang J, Xiao TJ: Functional-differential equations with infinite delay in Banach spaces. International Journal of Mathematics and Mathematical Sciences 1991,14(3):497-508. 10.1155/S0161171291000686
Mophou GM, N'Guérékata GM: Existence of mild solutions of some semilinear neutral fractional functional evolution equations with infinite delay. Applied Mathematics and Computation 2010,216(1):61-69. 10.1016/j.amc.2009.12.062
Mophou GM, N'Guérékata GM: A note on a semilinear fractional differential equation of neutral type with infinite delay. Advances in Difference Equations 2010, 2010:-8.
Hernández E, Henríquez HR: Existence of periodic solutions of partial neutral functional-differential equations with unbounded delay. Journal of Mathematical Analysis and Applications 1998,221(2):499-522. 10.1006/jmaa.1997.5899
Banaś J, Goebel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980:vi+97.
Heinz H-P: On the behaviour of measures of noncompactness with respect to differentiation and integration of vector-valued functions. Nonlinear Analysis: Theory, Methods & Applications 1983,7(12):1351-1371. 10.1016/0362-546X(83)90006-8
Agarwal RP, Meehan M, O'Regan D: Fixed Point Theory and Applications, Cambridge Tracts in Mathematics. Volume 141. Cambridge University Press, Cambridge, UK; 2001:x+170.
Szufla S: On the application of measure of noncompactness to existence theorems. Rendiconti del Seminario Matematico della Università di Padova 1986, 75: 1-14.
Zhou Y, Jiao F: Nonlocal Cauchy problem for fractional evolution equations. Nonlinear Analysis: Real World Applications 2010,11(5):4465-4475. 10.1016/j.nonrwa.2010.05.029
Mainardi F, Paradisi P, Gorenflo R: Probability distributions generated by fractional diffusion equations. In Econophysics: An Emerging Science. Edited by: Kertesz J, Kondor I. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000.
Bothe D: Multivalued perturbations of m -accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044
Acknowledgments
The authors are grateful to the referees for their valuable suggestions. F. Li is supported by the NSF of Yunnan Province (2009ZC054M). J. Zhang is supported by Tianyuan Fund of Mathematics in China (11026100).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, F., Zhang, J. Existence of Mild Solutions to Fractional Integrodifferential Equations of Neutral Type with Infinite Delay. Adv Differ Equ 2011, 963463 (2011). https://doi.org/10.1155/2011/963463
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/963463
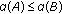 if
if 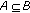 ,
, , where
, where 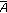 denotes the closure of
denotes the closure of 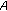 ,
,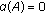 if and only if
if and only if 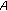 is precompact,
is precompact, ,
, 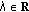 ,
,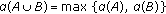 ,
,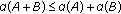 , where
, where  ,
,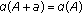 for any
for any 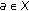 ,
, , where
, where 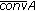 is the closed convex hull of
is the closed convex hull of 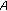 .
.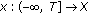 is continuous on
is continuous on 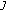 and
and 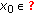 , then
, then  and
and 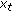 is continuous in
is continuous in 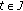 and
and
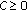 is a constant.
is a constant.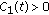 and a locally bounded function
and a locally bounded function 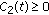 in
in 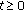 such that
such that
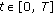 and
and  as in (1).
as in (1). is complete.
is complete.