Existence on positive solutions for boundary value problems of nonlinear fractional differential equations with p-Laplacian

Abstract

In this paper, we study the existence of positive solutions for the nonlinear fractional boundary value problem with a p-Laplacian operator

$$\begin{array}{c}{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)=f(t,u(t)),0<t<1,\hfill \\ u(0)=u^{\prime }(0)=u^{\prime }(1)=0,D_{0+}^{\alpha }u(0)=D_{0+}^{\alpha }u(1)=0,\hfill \end{array}$$

where $2<\alpha ⩽3$, $1<\beta ⩽2$, $D_{0+}^{\alpha }$, $D_{0+}^{\beta }$ are the standard Riemann-Liouville fractional derivatives, ${\varphi }_p(s)={|s|}^{p-2}s$, $p>1$, ${\varphi }_p^{-1}={\varphi }_q$, $1/p+1/q=1$, and $f(t,u)\in C([0,1]\times [0,+\mathrm{\infty }),[0,+\mathrm{\infty }))$. By the properties of Green’s function, the Guo-Krasnosel’skii fixed-point theorem, the Leggett-Williams fixed-point theorem, and the upper and lower solutions method, some new results on the existence of positive solutions are obtained. As applications, examples are presented to illustrate the main results.

MSC:34A08, 34B18, 35J05.

1 Introduction

Recently, fractional differential equations have been of great interest. The motivation for those works stems from both the intensive development of the theory of fractional calculus itself and the applications such as economics, engineering and other fields [1–7]. Many people pay attention to the existence and multiplicity of solutions or positive solutions for boundary value problems of nonlinear fractional differential equations by means of some fixed-point theorems [8–24] (such as the Schauder fixed-point theorem, the Guo-Krasnosel’skii fixed-point theorem, the Leggett-Williams fixed-point theorem) and the upper and lower solutions method [25–27].

To the best of our knowledge, there are few papers devoted to the study of fractional differential equations with a p-Laplacian operator [22–24, 26–29]. Its theories and applications seem to be just being initiated.

Wang et al.[26] considered the following p-Laplacian fractional differential equations boundary value problems:

$$\begin{array}{c}{D}_{0+}^{\gamma }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)=f(t,u(t)),0<t<1,\hfill \\ u(0)=0,u(1)=au(\xi ),D_{0+}^{\alpha }u(0)=0,D_{0+}^{\alpha }u(1)=b{D}_{0+}^{\alpha }u(\eta ),\hfill \end{array}$$

where $1<\alpha ,\gamma ⩽2$, $0⩽a,b⩽1$, $0<\xi ,\eta <1$, and $D_{0+}^{\alpha }$ is the standard Riemann-Liouville fractional derivative. ${\varphi }_p(s)={|s|}^{p-2}s$, $p>1$, ${\varphi }_p^{-1}={\varphi }_q$, $1/p+1/q=1$. They obtained the existence of at least one positive solution by means of the upper and lower solutions method.

Wang et al.[24] investigated the existence and multiplicity of concave positive solutions of a boundary value problem of a fractional differential equation with a p-Laplacian operator as follows:

$$\begin{array}{c}{D}_{0+}^{\gamma }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)+f(t,u(t),D_{0+}^{\rho }u(t))=0,0<t<1,\hfill \\ u(0)=u^{\prime }(1)=0,u^{″}(0)=0,D_{0+}^{\alpha }u(0)=0,\hfill \end{array}$$

where $2<\alpha <3$, $0<\gamma <1$, $0<\rho ⩽1$, $D_{0+}^{\alpha }$ is the Caputo derivative. By using a fixed-point theorem, some results for multiplicity of concave positive solutions are obtained.

Chen et al.[28] considered the boundary value problem for a fractional differential equation with a p-Laplacian operator at resonance

$$\begin{array}{c}{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }x(t))\right)=f(t,x(t),D_{0+}^{\alpha }x(t)),t\in [0,1],\hfill \\ D_{0+}^{\alpha }x(0)=D_{0+}^{\alpha }x(1)=0,\hfill \end{array}$$

where $0<\alpha ,\beta ⩽1$, $1<\alpha +\beta ⩽2$, and $D_{0+}^{\alpha }$ is the Caputo fractional derivative. By using the coincidence degree theory, a new result on the existence of solutions is obtained.

Guoqing Chai [29] investigated the existence and multiplicity of positive solutions for a class of boundary value problems of fractional differential equations with a p-Laplacian operator

$$\begin{array}{c}{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)+f(t,u(t))=0,0<t<1,\hfill \\ u(0)=0,u(1)+\sigma D_{0+}^{\gamma }u(1)=0,D_{0+}^{\alpha }u(0)=0,\hfill \end{array}$$

where $1<\alpha \le 2$, $0<\beta \le 1$, $0<\gamma \le 1$, $0\le \alpha -\gamma -1$, σ is a positive constant number, $D_{0+}^{\alpha }$, $D_{0+}^{\beta }$, $D_{0+}^{\gamma }$ are the standard Riemann-Liouville derivatives. By means of the fixed-point theorem on cones, some existence and multiplicity results of positive solutions are obtained.

Motivated by all the works above, in this paper, we deal with the following p-Laplacian fractional differential equation boundary value problem:

(1.1)

(1.2)

where $2<\alpha ⩽3$, $1<\beta ⩽2$, $D_{0+}^{\alpha }$, $D_{0+}^{\beta }$ are the standard Riemann-Liouville fractional derivatives and $f(t,u)\in C([0,1]\times [0,+\mathrm{\infty }),[0,+\mathrm{\infty }))$. By the properties of Green’s function, the Guo-Krasnosel’skii fixed-point theorem, the Leggett-Williams fixed-point theorem, and the upper and lower solutions method, some new results on the existence of positive solutions are obtained for the fractional differential equation boundary value problem (1.1) and (1.2).

The rest of this paper is organized as follows. In Section 2.7, we introduce some definitions and lemmas to prove our main results. In Section 3, we investigate the existence of a single positive solution for boundary value problems (1.1) and (1.2) by the upper and lower solutions method. In Section 4, we establish the existence of single and multiple positive solutions for boundary value problems (1.1) and (1.2) by fixed-point theorems. As applications, examples are presented to illustrate our main results in Section 3 and Section 4, respectively.

2 Preliminaries and lemmas

For the convenience of the reader, we give some background material from fractional calculus theory to facilitate the analysis of problem (1.1) and (1.2). These materials can be found in the recent literature, see [7, 8, 26, 27, 30–33].

Definition 2.1[7]

The fractional integral of order $\alpha >0$ of a function $y:(0,+\mathrm{\infty })\to \mathbb{R}$ is given by

$$I_{0+}^{\alpha }y(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-s)}^{\alpha -1}y(s)ds$$

provided the right-hand side is pointwise defined on $(0,+\mathrm{\infty })$.

Definition 2.2[7]

The fractional derivative of order $\alpha >0$ of a continuous function $y:(0,+\mathrm{\infty })\to \mathbb{R}$ is given by

$$D_{0+}^{\alpha }y(t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\left(\frac{d}{dt}\right)}^n{\int }_0^t\frac{y(s)}{{(t-s)}^{\alpha -n+1}}ds,$$

where n is the smallest integer greater than or equal to α, provided that the right-hand side is pointwise defined on $(0,+\mathrm{\infty })$.

Lemma 2.1[7]

Let$\alpha >0$. If we assume$u\in D_{0+}^{\alpha }u\in L^1(0,1)$, then the fractional differential equation

$$D_{0+}^{\alpha }u(t)=0$$

has

$$u(t)=c_1{t}^{\alpha -1}+c_2{t}^{\alpha -2}+\cdots +c_n{t}^{\alpha -n},c_i\in \mathbb{R},i=1,2,\dots ,n\mathit{\text{ as a unique solution}},$$

where n is the smallest integer greater than or equal to α.

Lemma 2.2[7]

Assume that$D_{0+}^{\alpha }u\in L^1(0,1)$with a fractional derivative of order$\alpha >0$. Then

$$I_{0+}^{\alpha }{D}_{0+}^{\alpha }u(t)=u(t)+c_1{t}^{\alpha -1}+c_2{t}^{\alpha -2}+\cdots +c_n{t}^{\alpha -n}$$

for some$c_i\in \mathbb{R}$, $i=1,2,\dots ,n$, where n is the smallest integer greater than or equal to α.

Lemma 2.3[27]

Let$y\in C[0,1]$and$2<\alpha ⩽3$. Then fractional differential equation boundary value problem

(2.1)

(2.2)

has a unique solution

$$u(t)={\int }_0^{1}G(t,s)y(s)ds,$$

where

$$G(t,s)=\{\begin{array}{cc}\frac{t^{\alpha -1}{(1-s)}^{\alpha -2}-{(t-s)}^{\alpha -1}}{\mathrm{\Gamma }(\alpha )},\hfill & s⩽t,\hfill \\ \frac{t^{\alpha -1}{(1-s)}^{\alpha -2}}{\mathrm{\Gamma }(\alpha )},\hfill & t⩽s.\hfill \end{array}$$

(2.3)

Lemma 2.4 Let$y\in C[0,1]$and$2<\alpha ⩽3$, $1<\beta ⩽2$. Then the fractional differential equation boundary value problem

(2.4)

(2.5)

has a unique solution

$$u(t)={\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )y(\tau )d\tau )ds,$$

where

$$H(t,s)=\{\begin{array}{cc}\frac{{[t(1-s)]}^{\beta -1}-{(t-s)}^{\beta -1}}{\mathrm{\Gamma }(\beta )},\hfill & s⩽t,\hfill \\ \frac{{[t(1-s)]}^{\beta -1}}{\mathrm{\Gamma }(\beta )},\hfill & t⩽s,\hfill \end{array}$$

(2.6)

$G(t,s)$is defined as (2.3).

Proof From Lemma 2.2 and $1<\beta ⩽2$, we have

$$I_{0+}^{\beta }{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)={\varphi }_p(D_{0+}^{\alpha }u(t))+c_1{t}^{\beta -1}+c_2{t}^{\beta -2}\text{for some }{c}_1,c_2\in \mathbb{R}.$$

In view of (2.4), we obtain

$$I_{0+}^{\beta }{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }u(t))\right)=I_{0+}^{\beta }y(t).$$

Therefore,

$${\varphi }_p(D_{0+}^{\alpha }u(t))=I_{0+}^{\beta }y(t)+C_1{t}^{\beta -1}+C_2{t}^{\beta -2}\text{for some }{C}_1,C_2\in \mathbb{R},$$

that is,

$${\varphi }_p(D_{0+}^{\alpha }u(t))={\int }_0^t\frac{{(t-\tau )}^{\beta -1}}{\mathrm{\Gamma }(\beta )}y(\tau )d\tau +C_1{t}^{\beta -1}+C_2{t}^{\beta -2}.$$

By the boundary conditions $D_{0+}^{\alpha }u(0)=D_{0+}^{\alpha }u(1)=0$, we have

$$C_2=0,C_1=-{\int }_0^1\frac{{(1-\tau )}^{\beta -1}}{\mathrm{\Gamma }(\beta )}y(\tau )d\tau .$$

Therefore, the solution $u(t)$ of fractional differential equation boundary value problem (2.4) and (2.5) satisfies

$$\begin{array}{rcl}{\varphi }_p(D_{0+}^{\alpha }u(t))& =& {\int }_0^t\frac{{(t-\tau )}^{\beta -1}}{\mathrm{\Gamma }(\beta )}y(\tau )d\tau -{\int }_0^1\frac{{[t(1-\tau )]}^{\beta -1}}{\mathrm{\Gamma }(\beta )}y(\tau )d\tau \\ =& -{\int }_0^{1}H(t,\tau )y(\tau )d\tau .\end{array}$$

Consequently, $D_{0+}^{\alpha }u(t)+{\varphi }_q({\int }_0^{1}H(t,\tau )y(\tau )d\tau )=0$. Thus, fractional differential equation boundary value problem (2.4) and (2.5) is equivalent to the following problem:

$$\begin{array}{c}{D}_{0+}^{\alpha }u(t)+{\varphi }_q({\int }_0^{1}H(t,\tau )y(\tau )d\tau )=0,0<t<1,\hfill \\ u(0)=u^{\prime }(0)=u^{\prime }(1)=0.\hfill \end{array}$$

Lemma 2.3 implies that fractional differential equation boundary value problem (2.4) and (2.5) has a unique solution

$$u(t)={\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )y(\tau )d\tau )ds.$$

The proof is complete. □

Lemma 2.5 Let$2<\alpha ⩽3$, $1<\beta ⩽2$. The functions$G(t,s)$and$H(t,s)$defined by (2.3) and (2.6), respectively, are continuous on$[0,1]\times [0,1]$and satisfy

• (1) $G(t,s)⩾0$, $H(t,s)⩾0$ for $t,s\in [0,1]$;

• (2) $G(t,s)⩽G(1,s)$, $H(t,s)⩽H(s,s)$ for $t,s\in [0,1]$;

• (3) $G(t,s)⩾t^{\alpha -1}G(1,s)$ for $t,s\in (0,1)$;

• (4) there exist two positive functions ${\delta }_1,{\delta }_2\in C[0,1]$ such that

  

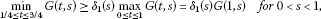  (2.7)
  

  (2.8)

Proof Observing the expression of $G(t,s)$ and $H(t,s)$, it is easy to see that $G(t,s)⩾0$ and $H(t,s)⩾0$ for $s,t\in [0,1]$.

From Lemma 3.1 in [27] and Lemma 2.4 in [8], we obtain (2) and (3).

In the following, we consider the existence of ${\delta }_1(s)$ and ${\delta }_2(s)$. Firstly, for given $s\in (0,1)$, $G(t,s)$ is increasing with respect to t for $t\in (0,1)$. Consequently, setting

$$g_1(t,s)=\frac{t^{\alpha -1}{(1-s)}^{\alpha -2}-{(t-s)}^{\alpha -1}}{\mathrm{\Gamma }(\alpha )},g_2(t,s)=\frac{t^{\alpha -1}{(1-s)}^{\alpha -2}}{\mathrm{\Gamma }(\alpha )},$$

we have

$$\begin{array}{rcl}\underset{1/4⩽t⩽3/4}{min}G(t,s)& =& \{\begin{array}{cc}{g}_1(\frac{1}{4},s),\hfill & s\in (0,\frac{1}{4}],\hfill \\ g_2(\frac{1}{4},s),\hfill & s\in [\frac{1}{4},1),\hfill \end{array}\\ =& \{\begin{array}{cc}\frac{1}{\mathrm{\Gamma }(\alpha )}[{(\frac{1}{4})}^{\alpha -1}{(1-s)}^{\alpha -2}-{(\frac{1}{4}-s)}^{\alpha -1}],\hfill & s\in (0,\frac{1}{4}],\hfill \\ \frac{1}{\mathrm{\Gamma }(\alpha )}{(\frac{1}{4})}^{\alpha -1}{(1-s)}^{\alpha -2},\hfill & s\in [\frac{1}{4},1).\hfill \end{array}\end{array}$$

Secondly, with the use of the monotonicity of $G(t,s)$, we have

$$\underset{0⩽t⩽1}{max}G(t,s)=G(1,s)=\frac{1}{\mathrm{\Gamma }(\alpha )}[{(1-s)}^{\alpha -2}-{(1-s)}^{\alpha -1}].$$

Thus, setting

$${\delta }_1(s)=\{\begin{array}{cc}\frac{{(\frac{1}{4})}^{\alpha -1}{(1-s)}^{\alpha -2}-{(\frac{1}{4}-s)}^{\alpha -1}}{{(1-s)}^{\alpha -2}-{(1-s)}^{\alpha -1}},\hfill & s\in (0,\frac{1}{4}],\hfill \\ \frac{{(\frac{1}{4})}^{\alpha -1}{(1-s)}^{\alpha -2}}{{(1-s)}^{\alpha -2}-{(1-s)}^{\alpha -1}},\hfill & s\in [\frac{1}{4},1),\hfill \end{array}$$

then (2.7) holds.

Similar to Lemma 2.4 in [8], we choose

$${\delta }_2(s)=\{\begin{array}{cc}\frac{{[\frac{3}{4}(1-s)]}^{\beta -1}-{(\frac{3}{4}-s)}^{\beta -1}}{{[s(1-s)]}^{\beta -1}},\hfill & s\in (0,r],\hfill \\ {(\frac{1}{4s})}^{\beta -1},\hfill & s\in [r,1).\hfill \end{array}$$

The proof is complete. □

Lemma 2.6 Let$2<\alpha ⩽3$. If$y(t)\in C[0,1]$and$y(t)⩾0$, then fractional differential equation boundary value problem (2.1) and (2.2) has a unique solution$u(t)⩾0$, $t\in [0,1]$.

Proof From Lemma 2.3, the fractional differential equation boundary value problem (2.1) and (2.2) has a unique solution

$$u(t)={\int }_0^{1}G(t,s)y(s)ds.$$

In view of Lemma 2.5, we know $G(t,s)$ is continuous on $[0,1]\times [0,1]$ and $G(t,s)⩾0$ for $t,s\in [0,1]$. If $y(t)\in C[0,1]$ and $y(t)⩾0$, we obtain $u(t)⩾0$. The proof is complete. □

Let $E_0=\{u:u\in C^3[0,1],{\varphi }_p(D_{0+}^{\alpha }u)\in C^2[0,1]\}$. Now, we introduce definitions about the upper and lower solutions of fractional differential equation boundary value problem (1.1) and (1.2).

Definition 2.3[26]

A function $\eta (t)$ is called an upper solution of fractional differential equation boundary value problem (1.1) and (1.2) if $\eta (t)\in E_0$ and $\eta (t)$ satisfies

$$\begin{array}{c}{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }\eta (t))\right)⩾f(t,\eta (t)),0<t<1,2<\alpha ⩽3,1<\beta ⩽2,\hfill \\ \eta (0)⩾0,{\eta }^{\prime }(0)⩾0,{\eta }^{\prime }(1)⩾0,\hfill \\ D_{0+}^{\alpha }\eta (0)⩽0,D_{0+}^{\alpha }\eta (1)⩽0.\hfill \end{array}$$

Definition 2.4[26]

A function $\xi (t)$ is called a lower solution of fractional differential equation boundary value problem (1.1) and (1.2) if $\xi (t)\in E_0$ and $\xi (t)$ satisfies

$$\begin{array}{c}{D}_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }\xi (t))\right)⩽f(t,\xi (t)),0<t<1,2<\alpha ⩽3,1<\beta ⩽2,\hfill \\ \xi (0)⩽0,{\xi }^{\prime }(0)⩽0,{\xi }^{\prime }(1)⩽0,\hfill \\ D_{0+}^{\alpha }\xi (0)⩾0,D_{0+}^{\alpha }\xi (1)⩾0.\hfill \end{array}$$

Definition 2.5[8]

The map θ is said to be a nonnegative continuous concave functional on a cone P of a real Banach space E provided that $\theta :P\to [0,+\mathrm{\infty })$ is continuous and

$$\theta (tx+(1-t)y)⩾t\theta (x)+(1-t)\theta (y)$$

for all $x,y\in P$ and $0⩽t⩽1$.

Lemma 2.7[8]

Let E be a Banach space, $P\subseteq E$be a cone, and${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$be two bounded open balls of E centered at the origin with${\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$. Suppose that$\mathcal{A}:P\cap ({\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1)\to P$is a completely continuous operator such that either

• (i) $\parallel \mathcal{A}x\parallel ⩽\parallel x\parallel$, $x\in P\cap \partial {\mathrm{\Omega }}_1$ and $\parallel \mathcal{A}x\parallel ⩾\parallel x\parallel$, $x\in P\cap \partial {\mathrm{\Omega }}_2$ or

• (ii) $\parallel \mathcal{A}x\parallel ⩾\parallel x\parallel$, $x\in P\cap \partial {\mathrm{\Omega }}_1$ and $\parallel \mathcal{A}x\parallel ⩽\parallel x\parallel$, $x\in P\cap \partial {\mathrm{\Omega }}_2$

holds. Then$\mathcal{A}$has a fixed point in$P\cap ({\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1)$.

Let $a,b,c>0$ be constants, $P_c=\{u\in P:\parallel u\parallel <c\}$, $P(\theta ,b,d)=\{u\in P:b⩽\theta (u),\parallel u\parallel ⩽d\}$.

Lemma 2.8[8]

Let P be a cone in a real Banach space E, $P_c=\{x\in P\mid \parallel x\parallel ⩽c\}$, θ be a nonnegative continuous concave functional on P such that$\theta (x)⩽\parallel x\parallel$for all$x\in {\overline{P}}_c$, and$P(\theta ,b,d)=\{x\in P\mid b⩽\theta (x),\parallel x\parallel ⩽d\}$. Suppose$\mathcal{B}:{\overline{P}}_c\to {\overline{P}}_c$is completely continuous and there exist constants$0<a<b<d⩽c$such that

(C1) $\{x\in P(\theta ,b,d)\mid \theta (x)>b\}\ne \mathrm{\varnothing }$and$\theta (\mathcal{B}x)>b$for$x\in P(\theta ,b,d)$;

(C2) $\parallel \mathcal{B}x\parallel <a$for$x⩽a$;

(C3) $\theta (\mathcal{B}x)>b$for$x\in P(\theta ,b,c)$with$\parallel \mathcal{B}x\parallel >d$.

Then ℬ has at least three fixed points$x_1$, $x_2$, and$x_3$with

$$\parallel x_1\parallel <a,b<\theta (x_2),a<\parallel x_3\parallel \mathit{\text{with}}\theta (x_3)<b.$$

Let $E=C[0,1]$ be endowed with $\parallel u\parallel ={max}_{0⩽t⩽1}|u(t)|$. Define the cone $P\subset E$ by

$$P=\{u\in E\mid u(t)⩾0\}.$$

Let the nonnegative continuous concave functional θ on the cone P be defined by

$$\theta (u)=\underset{1/4⩽t⩽3/4}{min}|u(t)|.$$

Lemma 2.9 Let $T:P\to E$ be the operator defined by

$$Tu(t):={\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds.$$

Then$T:P\to P$is completely continuous.

Proof Let $u\in P$, in view of the nonnegativeness and continuity of $G(t,s)$, $H(t,s)$, and $f(t,u(t))$, we have $T:P\to P$ is continuous.

Let $\mathrm{\Omega }\subset P$ be bounded, i.e., there exists a positive constant $M>0$ such that $\parallel u\parallel ⩽M$ for all $u\in \mathrm{\Omega }$. Let $L={max}_{0⩽t⩽1,0⩽u⩽M}|f(t,u)|+1$, then for $u\in \mathrm{\Omega }$, we have

$$\begin{array}{rcl}|Tu(t)|& =& |{\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds|\\ ⩽& L^{q-1}{\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )d\tau )ds\\ ⩽& L^{q-1}{\int }_0^{1}G(1,s){\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )ds\\ <& +\mathrm{\infty }.\end{array}$$

Hence, $T(\mathrm{\Omega })$ is uniformly bounded.

On the other hand, since $G(t,s)$ is continuous on $[0,1]\times [0,1]$, it is uniformly continuous on $[0,1]\times [0,1]$. Thus, for fixed $s\in [0,1]$ and for any $\epsilon >0$, there exists a constant $\delta >0$ such that any $t_1,t_2\in [0,1]$ and $|t_1-t_2|<\delta$,

$$|G(t_1,s)-G(t_2,s)|<\frac{\epsilon }{L^{q-1}{\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )}.$$

Then, for all $u\in \mathrm{\Omega }$,

$$\begin{array}{c}|Tu(t_2)-Tu(t_1)|\hfill \\ ⩽{\int }_0^1|G(t_2,s)-G(t_1,s)|{\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds\hfill \\ ⩽L^{q-1}{\int }_0^1|G(t_2,s)-G(t_1,s)|{\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )ds\hfill \\ =L^{q-1}{\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau ){\int }_0^1|G(t_2,s)-G(t_1,s)|ds\hfill \\ <\epsilon ,\hfill \end{array}$$

that is to say, $T(\mathrm{\Omega })$ is equicontinuous. By the Arzela-Ascoli theorem, we have $T:P\to P$ is completely continuous. The proof is complete. □

3 Existence of a single positive solution

In this section, for the sake of simplicity, we assume that

(H₁) $f(t,u)$ is nonincreasing to u;

(H₂) There exists a continuous function $p(t)⩾0$, $t\in [0,1]$ such that

(3.1)

(3.2)

Theorem 3.1 Assume that (H₁) and (H₂) hold. Then the fractional differential equation boundary value problem (1.1) and (1.2) has at least one positive solution$\gamma (t)$.

Proof From Lemma 2.9, we obtain $T(P)\subseteq P$. By direct computations, we have

(3.3)

(3.4)

Now, we prove that the functions $\eta (t)=Tp(t)$, $\xi (t)=Tq(t)$ are upper and lower solutions of fractional differential equation boundary value problem (1.1) and (1.2), respectively.

From (H₁) and (H₂), we have

$$p(t)⩽q(t)=Tp(t),Tq(t)⩽q(t)=Tp(t),t\in [0,1].$$

(3.5)

Hence, $\xi (t)⩽\eta (t)$. By $T(P)\subseteq P$, we know $\xi (t),\eta (t)\in P$. From (3.3)-(3.5) we have

(3.6)

(3.7)

that is, $\eta (t)$ and $\xi (t)$ are upper and lower solutions of fractional differential equation boundary value problem (1.1) and (1.2), respectively.

Next, we show that the fractional differential equation boundary value problem

(3.8)

(3.9)

has a positive solution, where

$$g(t,u(t))=\{\begin{array}{cc}f(t,\xi (t)),\hfill & \text{if }u(t)⩽\xi (t),\hfill \\ f(t,u(t)),\hfill & \text{if }\xi (t)⩽u(t)⩽\eta (t),\hfill \\ f(t,\eta (t)),\hfill & \text{if }\eta (t)⩽u(t).\hfill \end{array}$$

(3.10)

Thus, we consider the operator $B:P\to E$ defined as follows:

$$Bu(t):={\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )g(\tau ,u(\tau ))d\tau )ds,$$

where $G(t,s)$ and $H(t,s)$ are defined as (2.3) and (2.6), respectively. It is clear that $Bu(t)⩾0$ for all $u\in P$ and a fixed point of the operator B is a solution of the fractional differential equation boundary value problem (3.8) and (3.9).

Similar to Lemma 2.9, we know that B is a compact operator. By the Schauder fixed-point theorem, the operator B has a fixed point, that is, the fractional differential equation boundary value problem (3.8) and (3.9) has a positive solution.

Finally, we will prove that fractional differential equation boundary value problem (1.1) and (1.2) has at least one positive solution.

Suppose that $\gamma (t)$ is a solution of (3.8) and (3.9). Now, to complete the proof, it suffices to show that $\xi (t)⩽\gamma (t)⩽\eta (t)$, $t\in [0,1]$.

Let $\gamma (t)$ be a solution of (3.8) and (3.9). We have

$$\gamma (0)={\gamma }^{\prime }(0)={\gamma }^{\prime }(1)=0,D_{0+}^{\alpha }\gamma (0)=D_{0+}^{\alpha }\gamma (1)=0.$$

(3.11)

From (H₁), we have

$$f(t,\eta (t))⩽g(t,\gamma (t))⩽f(t,\xi (t)),t\in [0,1].$$

(3.12)

By (H₂) and (3.5), we obtain

$$f(t,q(t))⩽g(t,\gamma (t))⩽f(t,p(t)),t\in [0,1].$$

(3.13)

By $p(t)\in P$ and (3.3), we can get

$$D_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }\eta (t))\right)=D_{0+}^{\beta }\left({\varphi }_p(D_{0+}^{\alpha }(Tp)(t))\right)=f(t,p(t)),t\in [0,1].$$

(3.14)

Combining (3.4), (3.11)-(3.14), we have

(3.15)

(3.16)

Let $x(t)={\varphi }_p(D_{0+}^{\alpha }\eta (t))-{\varphi }_p(D_{0+}^{\alpha }\gamma (t))$. By (3.16), we obtain $x(0)=x(1)=0$.

By Lemma 2.6, we know $x(t)⩽0$, $t\in [0,1]$, which implies that

$${\varphi }_p(D_{0+}^{\alpha }\eta (t))⩽{\varphi }_p(D_{0+}^{\alpha }\gamma (t)),t\in [0,1].$$

Since ${\varphi }_p$ is monotone increasing, we obtain $D_{0+}^{\alpha }\eta (t)⩽D_{0+}^{\alpha }\gamma (t)$, that is, $D_{0+}^{\alpha }(\eta -\gamma )(t)⩽0$. By Lemma 2.6, (3.15) and (3.16), we have $(\eta -\gamma )(t)⩾0$. Therefore, $\eta (t)⩾\gamma (t)$, $t\in [0,1]$.

In a similar way, we can prove that $\xi (t)⩽\gamma (t)$, $t\in [0,1]$. Consequently, $\gamma (t)$ is a positive solution of fractional differential equation boundary value problem (1.1) and (1.2). This completes the proof. □

Example 3.1

We consider the following fractional differential equation boundary value problem:

(3.17)

(3.18)

Clearly, $f(t,u)=t^2+\frac{1}{\sqrt{u}}$ is nonincreasing relative to u. This shows that (H₁) holds.

Let $m(t)=t^{3/2}$. From Lemma 2.5, we have

$$\begin{array}{rcl}n(t)& :=& Tm(t)={\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,m(\tau ))d\tau )ds\\ =& {\int }_0^1\frac{G(t,s)}{G(1,s)}G(1,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,m(\tau ))d\tau )ds\\ ⩾& t^{\alpha -1}{\int }_0^{1}G(1,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,m(\tau ))d\tau )ds\end{array}$$

and $Tn(t)=T^{2}m(t)\in P$, there exist positive numbers $d_1$ and $d_2$ such that $Tm(t)⩾d_{1}m(t)$ and $T^{2}m(t)⩾d_{2}m(t)$.

Choosing a positive number $d_0⩽\{1,d_1\}$ and combining the monotonicity of T, we have

$$T(d_{0}m(t))⩾Tm(t)⩾d_{1}m(t)⩾d_{0}m(t),T^2(d_{0}m(t))⩾T(d_{0}m(t))⩾d_{0}m(t).$$

Taking $p(t)=d_0{t}^{3/2}$, then we have

That is, the condition (H₂) holds. By Theorem 3.1, the fractional differential equation boundary value problem (3.17) and (3.18) has at least one positive solution.

4 Existence of single and multiple positive solutions

In this section, for convenience, we denote

$$\begin{array}{c}M={({\int }_0^{1}G(1,s){\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )ds)}^{-1},\hfill \\ N={({\int }_{1/4}^{3/4}{\delta }_1(s)G(1,s){\varphi }_q({\int }_{1/4}^{3/4}{\delta }_2(\tau )H(\tau ,\tau )d\tau )ds)}^{-1}.\hfill \end{array}$$

Theorem 4.1 Let$f(t,u)$be continuous on$[0,1]\times [0,+\mathrm{\infty })$. Assume that there exist two positive constants$a_2>a_1>0$such that

(A1) $f(t,u)⩾{\varphi }_p(N{a}_1)$for$(t,u)\in [0,1]\times [0,a_1]$;

(A2) $f(t,u)⩽{\varphi }_p(M{a}_2)$for$(t,u)\in [0,1]\times [0,a_2]$.

Then the fractional differential equation boundary value problem (1.1) and (1.2) has at least one positive solution u such that$a_1⩽\parallel u\parallel ⩽a_2$.

Proof From Lemmas 2.3, 2.4, and 2.9, we get that $T:P\to P$ is completely continuous and fractional differential equation boundary value problem (1.1) and (1.2) has a solution $u=u(t)$ if and only if u solves the operator equation $u=Tu(t)$. In order to apply Lemma 2.7, we divide our proof into two steps.

Step 1. Let ${\mathrm{\Omega }}_1:=\{u\in P\mid \parallel u\parallel <a_1\}$. For $u\in \partial {\mathrm{\Omega }}_1$, we have $0⩽u(t)⩽a_1$ for all $t\in [0,1]$. It follows from (A1) that for $t\in [1/4,3/4]$,

$$\begin{array}{rcl}Tu(t)& =& {\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds\\ ⩾& {\int }_0^1{\delta }_1(s)G(1,s){\varphi }_q({\int }_0^1{\delta }_2(\tau )H(\tau ,\tau )f(\tau ,u(\tau ))d\tau )ds\\ ⩾& N{a}_1{\int }_{1/4}^{3/4}{\delta }_1(s)G(1,s){\varphi }_q({\int }_{1/4}^{3/4}{\delta }_2(\tau )H(\tau ,\tau )d\tau )ds\\ =& a_1=\parallel u\parallel .\end{array}$$

So,

$$\parallel Tu\parallel ⩾\parallel u\parallel \text{for }u\in \partial {\mathrm{\Omega }}_1.$$

Step 2. Let ${\mathrm{\Omega }}_2:=\{u\in P\mid \parallel u\parallel <a_2\}$. For $u\in \partial {\mathrm{\Omega }}_2$, we have $0⩽u(t)⩽a_2$ for all $t\in [0,1]$. It follows from (A2) that for $t\in [0,1]$,

$$\begin{array}{rcl}\parallel Tu(t)\parallel & =& \underset{0⩽t⩽1}{max}{\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds\\ ⩽& M{a}_2{\int }_0^{1}G(1,s){\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )ds\\ =& a_2=\parallel u\parallel .\end{array}$$

Therefore,

$$\parallel Tu\parallel ⩽\parallel u\parallel \text{for }u\in \partial {\mathrm{\Omega }}_2.$$

Then, by (ii) of Lemma 2.7, we complete the proof. □

Example 4.1

We consider the following fractional differential equation boundary value problem:

(4.1)

(4.2)

Let $p=2$. By a simple computation, we obtain $M=11.25$, $N\approx 736.6099$. Choosing $a_1=0.003$, $a_2=0.25$, therefore

$$\begin{array}{c}f(t,u)=\frac{5}{2}+\frac{\sqrt{u}}{10}+\frac{t^2}{4}⩾2.5>{\varphi }_p(N{a}_1)\approx 2.2098\text{for }(t,u)\in [0,1]\times [0,0.003],\hfill \\ f(t,u)=\frac{5}{2}+\frac{\sqrt{u}}{10}+\frac{t^2}{4}⩽2.8<{\varphi }_p(M{a}_2)=2.8125\text{for }(t,u)\in [0,1]\times [0,0.25].\hfill \end{array}$$

With the use of Theorem 4.1, the fractional differential equation boundary value problem (4.1) and (4.2) has at least one solution u such that $0.003⩽\parallel u\parallel ⩽0.25$.

Theorem 4.2 Let$f(t,u)$be continuous on$[0,1]\times [0,+\mathrm{\infty })$. Assume that there exist constants$0<a<b<c$such that the following assumptions hold:

(B1) $f(t,u)<{\varphi }_p(Ma)$for$(t,u)\in [0,1]\times [0,a]$;

(B2) $f(t,u)⩾{\varphi }_p(Nb)$for$(t,u)\in [1/4,3/4]\times [b,c]$;

(B3) $f(t,u)⩽{\varphi }_p(Mc)$for$(t,u)\in [0,1]\times [0,c]$.

Then the fractional differential equation boundary value problem (1.1) and (1.2) has at least three positive solutions$u_1$, $u_2$, and$u_3$with

$$\begin{array}{c}\underset{0⩽t⩽1}{max}|u_1(t)|<a,b<\underset{1/4⩽t⩽3/4}{min}|u_2(t)|<\underset{0⩽t⩽1}{max}|u_2(t)|⩽c,\hfill \\ a<\underset{0⩽t⩽1}{max}|u_3(t)|⩽c,\underset{1/4⩽t⩽3/4}{min}|u_3(t)|<b.\hfill \end{array}$$

Proof From Lemmas 2.3, 2.4, and 2.9, we have $T:P\to P$ is completely continuous and fractional differential equation boundary value problem (1.1) and (1.2) has a solution $u=u(t)$ if and only if u satisfies the operator equation $u=Tu(t)$.

We show that all the conditions of Lemma 2.8 are satisfied. If $u\in {\overline{P}}_c$, then $\parallel u\parallel ⩽c$. By (B3), we have

$$\begin{array}{rcl}\parallel Tu(t)\parallel & =& \underset{0⩽t⩽1}{max}|{\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds|\\ ⩽& Mc{\int }_0^{1}G(1,s){\varphi }_q({\int }_0^{1}H(\tau ,\tau )d\tau )ds\\ ⩽& c.\end{array}$$

Hence, $T:{\overline{P}}_c\to {\overline{P}}_c$. In the same way, if $u\in {\overline{P}}_a$, then assumption (B1) yields $\parallel Tu\parallel <a$. Therefore, condition (C2) of Lemma 2.8 is satisfied.

To check condition (C1) of Lemma 2.6, we choose $u(t)=(b+c)/2$, $0⩽t⩽1$. It is easy to see that $u(t)=(b+c)/2\in P(\theta ,b,c)$, $\theta (u)=\theta ((b+c)/2)>b$; consequently, $\{u\in P(\theta ,b,c)\mid \theta (u)>b\}\ne \mathrm{\varnothing }$. Hence, if $u\in P(\theta ,b,c)$, then $b⩽u(t)⩽c$ for $1/4⩽t⩽3/4$. From assumption (B2), we have $f(t,u(t))⩾{\varphi }_p(Nb)$ for $1/4⩽t⩽3/4$. So,

$$\begin{array}{rcl}\theta (Tu)& =& \underset{1/4⩽t⩽3/4}{min}|(Tu)(t)|⩾\underset{1/4⩽t⩽3/4}{min}{\int }_0^{1}G(t,s){\varphi }_q({\int }_0^{1}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds\\ >& {\int }_{1/4}^{3/4}\underset{1/4⩽t⩽3/4}{min}G(t,s){\varphi }_q({\int }_{1/4}^{3/4}\underset{1/4⩽t⩽3/4}{min}H(s,\tau )f(\tau ,u(\tau ))d\tau )ds\\ ⩾& Nb{\int }_{1/4}^{3/4}{\delta }_1(s)G(1,s){\varphi }_q({\int }_{1/4}^{3/4}{\delta }_2(\tau )H(\tau ,\tau )d\tau )ds\\ =& b,\end{array}$$

i.e., $\theta (Tu)>b$ for all $u\in P(\theta ,b,c)$. Choosing $d=c$, this shows that condition (C1) of Lemma 2.8 is also satisfied.

In the same way, if $u\in P(\theta ,b,c)$ and $\parallel Tu\parallel >c=d$, we also obtain $\theta (Tu)>b$. Then condition (C3) of Lemma 2.8 is also satisfied.

By Lemma 2.8, the fractional differential equation boundary value problem (1.1) and (1.2) has at least three positive solutions $u_1$, $u_2$, and $u_3$, satisfying

$$\begin{array}{c}\underset{0⩽t⩽1}{max}|u_1(t)|<a,b<\underset{1/4⩽t⩽3/4}{min}|u_2(t)|,\hfill \\ a<\underset{0⩽t⩽1}{max}|u_3(t)|,\underset{1/4⩽t⩽3/4}{min}|u_3(t)|<b.\hfill \end{array}$$

The proof is complete. □

Example 4.2

We consider the following fractional differential equation boundary value problem:

(4.3)

(4.4)

where

$$f(t,u)=\{\begin{array}{cc}\frac{t}{100}+737u^2\hfill & \text{for }u⩽1,\hfill \\ \frac{t}{100}+u+736\hfill & \text{for }u>1.\hfill \end{array}$$

Let $p=2$. We obtain $M=11.25$, $N\approx 736.6099$. Choosing $a=0.01$, $b=1$, $c=72$, therefore

With the use of Theorem 4.2, the fractional differential equation boundary value problem (4.3) and (4.4) has at least three positive solutions $u_1$, $u_2$, and $u_3$ with

$$\begin{array}{c}\underset{0⩽t⩽1}{max}|u_1(t)|<0.01,1<\underset{1/4⩽t⩽3/4}{min}|u_2(t)|<\underset{0⩽t⩽1}{max}|u_2(t)|⩽72,\hfill \\ 0.01<\underset{0⩽t⩽1}{max}|u_3(t)|⩽72,\underset{1/4⩽t⩽3/4}{min}|u_3(t)|<1.\hfill \end{array}$$