- Research
- Open access
- Published:
Ulam–Hyers stability analysis to a class of nonlinear implicit impulsive fractional differential equations with three point boundary conditions
Advances in Difference Equations volume 2019, Article number: 7 (2019)
Abstract
In this article, we discuss the sufficient conditions for the existence, uniqueness and stability of solutions to a class of nonlinear impulsive boundary value problem of fractional order differential equations. Using classical fixed point theorems, we develop the required conditions. Further, using the techniques of nonlinear functional analysis, we investigate Ulam–Hyers stability results to the proposed problem. For applications of our derived results, we present two numerical examples.
1 Introduction
The concept of fractional calculus has been introduced in 1695, when in a letter to Leibnitz, L’Hospital asked a question about the derivative of order \(q=1/2\). This question was proved a base for the generalization of classical calculus to fractional calculus. Later on, for the first time Lacroix [23] introduced the fractional derivative. In 19th and 20th century, Abel, Riemman and Liouvilli formally developed the concepts of fractional derivatives and integrals. Recently the fractional calculus has become an attractive area of research. One can see its enormous number of applications in different fields of science and engineering like physics, chemistry, finance, diffusion processes, modeling of mechanical properties of materials, signal processing, image processing, modeling of the behavior of viscoelastic and visco-plastic materials under external influences, bioengineering, description of mechanical systems, control theory, psychology phenomenons, etc. For more about this area and its applications, we refer to [1,2,3,4,5, 8, 9, 11,12,13,14, 21, 22, 25, 26] and the references therein.
The impulsive differential equations constitute an important class of differential equations. These equations arise as a result of modeling the processes subject to abrupt (sudden) changes and discontinuous jumps occur in their states with respect to different intervals of time. Such a phenomenon is naturally seen in various subjects of science like physics, dynamics, geology, geography, biology, engineering and management sciences, etc. Due to the significant applications of impulsive differential equations, this area has got much importance and attention. For its general study and applications, we refer to [10, 27, 30,31,32, 35, 39, 41] and the references therein.
On the research side of both classical and fractional calculus, fixed point theory and mathematical inequalities play an important role. Researchers use different techniques to investigate the existence and uniqueness of solutions to various systems of differential equations, we refer to [6, 7, 29].
On other hand, stability analysis has got too much importance on research side. It is very important from numerical and optimization point of view in investigating various problems of physics, mathematical biology, biophysics, economics, where the actual solution is almost difficult. In literature, we come across different approaches towards stability analysis. However, in this paper we discuss the Ulam–Hyers (UH) stability approach which is comparatively the most simple and easy way of investigation the stability of systems. Its history goes back to the middle of the 19th century. In 1940 Ulam posed the question in a seminar held at Wisconsin University “Under what conditions does there exist an additive mapping near an approximately additive mapping?” (see [33, 34]). In 1941, Hyers [18] found the solution to Ulam’s question in the case of Banach spaces. In the year 1978, Rassias investigated the UH stability for linear and nonlinear mappings. In 1988, Jung (see [19, 20]) established the UH stability of more general mappings on restricted domains. In 1993, Obloza [24] established the UH stability of linear differential equations. Later on many researchers generalized these results in many directions.
Impulsive boundary value problems (BVPs) corresponding to integer order differential equations with impulsive conditions have been considered extensively in the literature, but in the case of non-integer order differential equations the problems still need further investigation under impulsive conditions. The aforesaid stability has been investigated for a class of linear fractional order differential equations (FDEs) [38]. Also the above results have been recently extended to semilinear differential equations, impulsive differential equations and partial differential equations, for detail see [16, 36]. Wang et al. [37], studied the above results for a fractional order differential switched systems with coupled nonlocal initial and impulsive conditions.
Recently, Benchohra et al. [15], studied the existence and uniqueness of solution for a class of initial value problems with impulsive conditions given by

where  is the Caputo fractional derivative, \(f : J\times \mathbf{R}\times \mathbf{R}\rightarrow \mathbf{R}\) is a given continuous function.
is the Caputo fractional derivative, \(f : J\times \mathbf{R}\times \mathbf{R}\rightarrow \mathbf{R}\) is a given continuous function.
The aim of this paper is to study existence, uniqueness of solution and UH stability analysis to the following BVP of implicit impulsive fractional differential equations:

where \(f:J\times \mathbf{R}\times \mathbf{R}\rightarrow \mathbf{R}\) and  , are nonlinear continuous functions for
, are nonlinear continuous functions for  . Further
. Further  ,
,  , where
, where  and
and  denote the right and left-hand limit of the function \(\theta (t)\), respectively, at
denote the right and left-hand limit of the function \(\theta (t)\), respectively, at  . Similarly
. Similarly  and
and  denote the right and left-hand limit of the function \(\theta '(t)\), respectively, at
denote the right and left-hand limit of the function \(\theta '(t)\), respectively, at  . Also, \(0=t_{0}< t_{1}<\cdots <t_{ \mathbf{b}}<t_{\mathbf{b}+1}=1\); b is a positive integer.
. Also, \(0=t_{0}< t_{1}<\cdots <t_{ \mathbf{b}}<t_{\mathbf{b}+1}=1\); b is a positive integer.
For existence of solution, we use Schaefer’s fixed point theorem while for investigation of uniqueness result, we use Banach’s fixed point theorem. For applications of our obtained results, we give two numerical examples.
2 Preliminaries and background materials
In this section, we introduce some notations, spaces and definitions and previous results which are used throughout this manuscript. We divide the interval \(J=[0,1]\) into sub intervals \([0,t_{1}], (t_{1},t_{2}], (t _{2},t_{3}],\ldots ,(t_{\mathbf{b}-1},t_{\mathbf{b}}], (t_{ \mathbf{b}},1]\), and denote these sub intervals by \(J_{0}\), \(J_{1}\), \(J_{2}\), …, \(J_{\mathbf{b}-1}\), \(J_{\mathbf{b}}\), respectively. Let \(\acute{J}=J\setminus \{t_{1},t_{2},t_{3},\dots ,t_{\mathbf{b}} \}\). Define the space by

Obviously \((\operatorname{PC}(J,\mathbf{R}),\|\theta \|_{\operatorname{PC}(J,\mathbf{R})})\) with the norm \(\|\theta \|_{\operatorname{PC}}=\sup_{t\in J}|\theta (t)|\) is a Banach space.
Definition 2.1
([26])
The fractional integral of order \(q\in \mathbf{R_{+}}\) for a function \(h:(0, \infty )\rightarrow \mathbf{R}\) is defined by
where Γ is the Euler gamma function defined by \(\varGamma (q)= \int _{0}^{\infty }t^{q-1}e^{-t}\,dt\), with \(q>0\). Further the integral on the right side is pointwise defined on \((0, \infty )\).
Definition 2.2
([21])
The Caputo derivative of fractional order \(q>0\) of a function \(h:(0, \infty )\rightarrow \mathbf{R}\) is defined by
Here \(n=[q]+1\) and \([q]\) represents the integer part of the real number q, and the integral on the right side is pointwise defined on \((0, \infty )\).
Lemma 2.3
([21])
For \(q>0\), we have the following result:
Lemma 2.4
([40])
The given FDE
has a solution given by
where \(c_{i}\in \mathbf{R}\), \(i=0\), \(1,2,3,\dots ,n-1\), \(n=[q]+1\).
For the UH’s type stability concepts to the concerned problem, we need the following inequalities. Let \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\), and there exist a constant \(\varphi >0\), \(\epsilon >0\) and nondecreasing function \(\vartheta \in C(J, \mathbf{R})\), such that the following inequalities exist:


and

Definition 2.5
([28])
The problem (1) is UH stable if there exists a real number \(c_{f,\mathbf{b}}>0\), such that, for each \(\epsilon >0\) and to each solution \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) of the inequality (2), there exists a unique solution \(\theta \in \operatorname{PC}(J, \mathbf{R})\) of the problem (1) such that
holds.
Definition 2.6
([28])
The problem (1) is GUH stable if there exists \(\psi _{f,\mathbf{b}}\in C(\mathbf{R_{+}},\mathbf{R_{+}})\), \(\psi _{f,\mathbf{b}}(0)=0\), such that, for each solution \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) of the inequality (2), there exists a unique solution \(\theta \in \operatorname{PC}(J,\mathbf{R})\) to the problem (1) such that
holds.
Definition 2.7
([28])
The problem (1) is UHR stable with respect to \((\vartheta ,\varphi )\), if there exists a real number \(c_{f, \mathbf{b},\vartheta }>0\), such that, for each \(\epsilon >0\) and every solution \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) of the inequality (3), there exists a unique solution \(\theta \in \operatorname{PC}(J,\mathbf{R})\) of the problem (1) such that
holds.
Definition 2.8
([28])
The problem (1) is GUHR stable with respect to \((\vartheta ,\varphi )\), if there exists a real number \(c_{f, \mathbf{b},\vartheta }>0\), such that, for each solution \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) of the inequality (4), there exists a unique solution \(\theta \in \operatorname{PC}(J,\mathbf{R})\) to the problem (1) such that
holds.
Remark 2.9
A function \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) is a solution of the inequality (2), if there exist a function \(\phi \in \operatorname{PC}(J,\mathbf{R})\) and a sequence  ,
,  (which depend on Θ only) such that
(which depend on Θ only) such that
-
(i)
\(|\phi (t)|\leq \epsilon \),
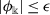 ,
,  ,
, 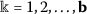 ;
; -
(ii)
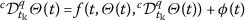 ,
,  ,
, 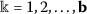 ;
; -
(iii)
 ,
, 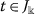 ,
, 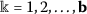 ;
; -
(iv)
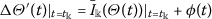 ,
, 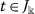 ,
, 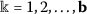 .
.
Remark 2.10
A function \(\varTheta \in \operatorname{PC}(J,\mathbf{R})\) is a solution of the inequality (4), if there exist a function \(\phi \in \operatorname{PC}(J,\mathbf{R})\) and a sequence  ,
,  (which depend on Θ only) such that
(which depend on Θ only) such that
-
(i)
\(|\phi (t)|\leq \epsilon \vartheta (t)\),
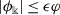 ,
, 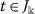 ,
, 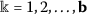 ;
; -
(ii)
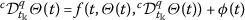 ,
, 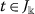 ,
, 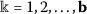 ;
; -
(iii)
 ,
, 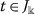 ,
, 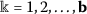 ;
; -
(iv)
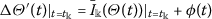 ,
, 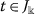 ,
, 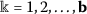 .
.
Similarly, one can state the remark for the inequality (3) in the same way.
Theorem 2.11
((Banach’s fixed point theorem) [17])
Let C be a non-empty closed subset of a Banach space E. Then any contraction mapping \(\mathcal{F}\) from C into itself has a unique fixed point.
Theorem 2.12
((Schaefer’s fixed point theorem) [17])
Let E be a Banach space and \(\mathcal{F} : \mathbf{E}\rightarrow \mathbf{E}\) is a completely continuous operator and the set \(\mathbf{D} = \{\theta \in \mathbf{E} :\theta = \mu \mathcal{F}\theta , 0<\mu <1\}\) is bounded. Then \(\mathcal{F}\) has a fixed point in E.
3 Main results
In this section, we study the existence and uniqueness of solution to the proposed class of impulsive BVP of implicit FDEs.
Lemma 3.1
Let \(1< q\leq 2\) and assume that \(\sigma : J\rightarrow \mathbf{R}\) be a continuous function. Then the solution \(\theta \in \operatorname{PC}(J, \mathbf{R})\) of the following implicit impulsive BVP:

is given by fractional integral equation as

where
and \(\delta =1-\lambda \eta \), \(\lambda \eta <1\).
Proof
Assume that θ is a solution of problem (5), then, for any \(t\in J_{0}\), there exist constants \(c_{1},c_{2}\in \mathbf{R}\) such that
Similarly for \(t\in J_{1}\), there exist constants \(d_{1},d_{2}\in \mathbf{R}\), such that
In view of
we get
Consequently,
By a similar way repeating the same process, we get

Applying the given boundary conditions \(\theta (0)=0\) and \(\theta (1)= \lambda \theta (\eta )\), we get \(c_{1}=0\) and

Substituting these values of \(c_{1}\) and \(c_{2}\) in (7) and (9), we get (6). □
Assume that, for any \(v, \bar{v}, x, \bar{x}\in \mathbf{R}\), \(t\in J\), the following hypotheses hold:
- \((H_{1})\) :
-
The function \(f : J\times \mathbf{R}\times \mathbf{R}\rightarrow \mathbf{R}\) is continuous;
- \((H_{2})\) :
-
there exists a constant \(0< L<1\), such that
$$ \bigl\vert f(t,v,x)-f(t,\bar{v},\bar{x}) \bigr\vert \leq L\bigl( \vert v- \bar{v} \vert + \vert x-\bar{x} \vert \bigr); $$ - \((H_{3})\) :
-
there exists a constant \(m>0\) such that
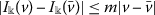 ;
; - \((H_{4})\) :
-
there exists a constant \(l>0\) such that
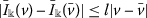 .
.
Note: For simplicity we shall use  .
.
Theorem 3.2
Under the hypotheses \((H_{1})\)–\((H_{4})\), and if the inequality
holds, then problem (1) has a unique solution.
Proof
We define an operator \(\mathcal{F}:\operatorname{PC}(J,\mathbf{R})\rightarrow \operatorname{PC}(J, \mathbf{R})\) by

We look for the fixed points. For this purpose we take \(\theta ,\bar{ \theta }\in \operatorname{PC}(J,\mathbf{R})\) and, for each \(t \in J\), we consider

Here
By \((H_{2})\), we get
Then
Using (13),  , \(t\leq 1\), and taking the maximum on both sides of (12), we have
, \(t\leq 1\), and taking the maximum on both sides of (12), we have
We use
Hence, by Banach’s fixed point theorem \(\mathcal{F}\) is a contraction and hence it has a unique fixed point, that is the unique solution of our considered problem (1). □
Introduce the following hypotheses:
- \((H_{5})\) :
-
There exist constants \(\alpha , \beta , \gamma \in C(J,\mathbb{R_{+}})\), such that
$$ \bigl\vert f\bigl(t, \theta (t), \sigma _{\theta }(t)\bigr) \bigr\vert \leq \alpha (t)+\beta (t) \vert \theta \vert +\gamma (t) \vert \sigma _{\theta } \vert ,\quad \mbox{for } t \in J, \theta , \bar{ \theta } \in \mathbf{R}, $$with \(\alpha ^{*}=\sup_{t\in J}\alpha (t)\), \(\beta ^{*}=\sup_{t\in J} \beta (t)\) and \(\gamma ^{*}=\sup_{t\in J}\gamma (t)<1\);
- \((H_{6})\) :
-
the functions \(I_{i}:\mathbf{R}\rightarrow \mathbf{R}\) are continuous and there exist constants \(M^{*}, N^{*}>0\), such that
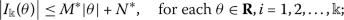
- \((H_{7})\) :
-
the functions \(\bar{I}_{i}:\mathbf{R}\rightarrow \mathbf{R}\) are continuous and there exist constants \(F^{*}, G^{*}>0\), such that
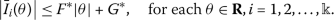
Theorem 3.3
Assume \((H_{1})\), \((H_{2})\), \((H_{5})\)–\((H_{7})\) hold, then problem (1) has at leat one solution.
Proof
Consider the operator \(\mathcal{F}\) defined in theorem 3.2. Via Schaefer’s fixed point theorem we prove that \(\mathcal{F}\) has a fixed point. The proof completes in four steps.
Step 1: \(\mathcal{F}\) is continuous. Let \(\{\theta _{n}\}\) be a sequence such that \(\theta _{n}\rightarrow \theta \in \operatorname{PC}(J, \mathbf{R})\). Then, for each \(t\in J\), we have

where
and
In view of \((H_{2})\), we have
Thus
Since \(\theta _{n}\rightarrow \theta \), consequently \(\sigma ^{(n)}_{ \theta }(t)\rightarrow \sigma _{\theta }(t)\) as \(n\rightarrow \infty \), for each \(t\in J\). Applying the Lebesgue dominated convergent theorem, the right hand side of (15) goes to zero as \(n\rightarrow \infty \). Hence
Thus
Hence \(\mathcal{F}\) is continuous.
Step 2: \(\mathcal{F}\) maps bounded set into bounded set in \(\operatorname{PC}(J,\mathbf{R})\). We need to show that, for any \(\mu ^{*}>0\), there exists a positive constant ρ such that, for each \(\theta \in \varOmega _{\mu ^{*}}=\{\theta \in \operatorname{PC}(J,\mathbf{R}) : \|\theta \|_{\operatorname{PC}} \leq \mu *\}\), we have \(\|\mathcal{F}(\theta )\|_{\operatorname{PC}}\leq \rho \). Therefore, for each \(t\in J\), we have

Using \((H_{5})\), we have for each \(t\in J\)
where \(\alpha ^{*}\), \(\beta ^{*}\), \(\gamma ^{*}\) are defined in \((H_{5})\).
The last result implies that

Thus, we have
Step 3: \(\mathcal{F}\) maps bounded set into equi-continuous set. Take \(t_{1}\), \(t_{2}\in J\) with \(t_{1}< t_{2}\) and let \(\varOmega _{\mu ^{*}}\) be a bounded set of \(\operatorname{PC}(J,\mathbf{R})\) as in the previous Step 2, then, for \(\theta \in \varOmega _{\mu ^{*}}\), we have

Using inequality (17) and hypotheses \((H_{6})\), \((H_{7})\), we have

The right hand side of (18) goes to zero as \(t_{1}\rightarrow t_{2}\), consequently
As a result of Steps 1 to 3 together with the Arzela–Ascoli theorem, we see that \(\mathcal{F}\) is completely continuous.
Step 4: A priori bound.
Finally, we show that the set \(\varOmega _{\mu ^{*}}=\{\theta \in \operatorname{PC}(J, \mathbf{R}) : \theta = \mu \mathcal{F}(\theta ) \text{ for some } 0< \mu <1\}\) is bounded. Let \(\theta \in \varOmega _{\mu ^{*}}\), then \(\theta = \mu \mathcal{F}(\theta )\), for some \(0<\mu <1\), we have for each \(t \in J\)

Using (17) and \((H_{5})\)–\((H_{7})\), we have

After rearranging the terms, we get
Taking the maximum on both sides and using for simplicity the notion
and
we get
From this we have
This implies that the set \(\varOmega _{\mu ^{*}}\) is bounded, hence by Schaefer’s fixed point theorem, we can say that \(\mathcal{F}\) has at least one fixed point which is a solution of our problem (5). □
4 UH stability analysis of IBVP (5)
In this section, we develop some adequate conditions under which the proposed problem (5) satisfies the assumptions of various kinds of UH stability.
Lemma 4.1
Let \(1 < q \leq 2\), if \(\theta \in \operatorname{PC}(J,\mathbf{R})\) is the solution of the inequality (2), then θ is a solution of the following inequality:
Proof
Since Θ is a solution of inequality (2) and in view of remark 2.9, we have

Obviously, the solution of (20) will be

where \(\delta =1-\eta \).
For the sake of simplicity, let us denote the sum of terms free of ϕ by \(F(t)\), that is,

Then we have from the above

This upon simplification yields
From which it implies that
□
- \((H_{8})\) :
-
There exists \(\varpi _{\vartheta }>0\) for the nondecreasing function \(\vartheta \in C(J,\mathbf{R})\), such that, for any \(t\in J\), the inequality
$$ I^{q}\vartheta (t)\leq \varpi _{\vartheta }\vartheta (t)\quad \text{and consequently } I^{q-1}\vartheta (t)\leq \varpi _{\vartheta } \vartheta (t) $$hold.
Lemma 4.2
If \(\theta \in \operatorname{PC}(J,\mathbf{R})\) is the solution of the inequality (4), then θ satisfies the following inequality:
Proof
From the proof of Lemma 4.1, we have the following inequality:

By Remark 2.10 and hypothesis \((H_{8})\), we get
This implies that
□
Theorem 4.3
Assume that the hypotheses \((H_{1})\)–\((H_{4})\) hold and if
then the IBVP (5) is UH stable and consequently GUH stable.
Proof
Let \(\theta \in \operatorname{PC}(J,\mathbf{R})\) be any solution of inequality (2) and θ̄ be a unique solution of problem (5), then we have
In view of Lemma 4.1, from (21) one has

Using \((H_{2})\) we have
From this we have
Using \((H_{3})\), \((H_{4})\) and (23), for each \(t\in J\), (22) implies that
Simplifying, we have
Therefore, we have
From this we conclude that the problem (5) is UH stable. Further if we set \(\psi (\epsilon )=c_{f,\mathbf{b}}(\epsilon )\); \(\psi (0)=0\), then the problem is GUH stable. □
Theorem 4.4
Under the hypotheses \((H_{1})\)–\((H_{4})\), \((H_{8})\) and if
is satisfied, then the IBVP (5) is UHR stable with respect to \((\vartheta ,\varphi )\), consequently GUHR stable.
Proof
Let \(\theta \in \operatorname{PC}(J,\mathbf{R})\) be the solution of inequality (4) and let θ be the unique solution of the IBVP (5), then, for each \(t\in J\), we have
By Lemma 4.2, we have
and from the proof of Theorem 4.3, we get
Hence the inequality (24) becomes
This implies that
Hence
where
This shows that the problem (5) is UHR stable.
Consequently, it can easily be shown that the problem (5) is GUHR stable. □
5 Example
To demonstrate our main results, we provide the following examples.
Example 5.1
Consider the BVP given by
From (25), we see that \(q=\frac{3}{2}\), \(\lambda =\frac{1}{2}\), \(\eta =\frac{1}{2}\), \(\mathbf{b}=1\). Set
Obviously, the function f is continuous.
Now for any \(v, \bar{v}, x, \bar{x}\in \mathbf{R}\), we have
Hence \((H_{2})\) satisfied with \(L=\frac{1}{20}\). For \((H_{3})\) and \((H_{4})\), let
For each \(\theta , \bar{\theta }\in \operatorname{PC}(J,\mathbf{R})\), \(t\in J\), we have
and
Hence \((H_{3})\) and \((H_{4})\) are satisfied with \(m=\frac{1}{40}\), \(l= \frac{1}{20}\). Also \(\delta =1-\eta =\frac{1}{2}\). Therefore, we have
Hence in view of Theorem 3.2, the given impulsive BVP (25) has a unique solution. From the conditions of Theorem 4.3 it follows that the given IBVP (25) is UH stable and consequently GUH stable.
For \(\vartheta (t)=t\), \(\varphi =1 \) we have
consequently
hence condition \((H_{8})\) is satisfied with \(\omega _{\vartheta }=\frac{2}{\sqrt{ \pi }}\), therefore, all the conditions of Theorem 4.4 are satisfied, thus the given IBVP (25) is UHR stable with respect to \((\vartheta ,\varphi )\). Further it is also obvious that the given IBVP (25) is GUHR stable.
Example 5.2
For the verification we take another example:
Here \(q=\frac{3}{2}\), \(\lambda =\frac{1}{3}\), \(\eta =\frac{1}{5}\), \(\mathbf{b}=1\). We set
The continuity of f is obvious.
For any \(v, x\in \mathbf{R}\), we have
We see that \(\alpha (t)=\frac{1}{13e^{t+20}}\), \(\beta (t)=\gamma (t)=\frac{1}{130e ^{t+20}}\). We see that \(\alpha ^{*}=\sup_{t\in J}\alpha (t)=\frac{1}{13e ^{20}}\), \(\beta ^{*}=\sup_{t\in J}\beta (t)=\frac{1}{130e^{20}}\) and \(\gamma ^{*}=\sup_{t\in J}\gamma (t)=\frac{1}{130e^{20}}<1\). This satisfies \((H_{5})\). Let
Then, for any \(\theta \in \operatorname{PC}(J,\mathbf{R})\), \(t\in J\), we have
and
The first inequality satisfies \((H_{6})\) with \(M^{*}=\frac{1}{25}>0\), \(N^{*}=1>0\) and the second inequality satisfies \((H_{7})\) with \(F^{*}=\frac{1}{25}>0\), \(G^{*}=1>0\). Therefore, by Theorem 3.3, problem (26) has at least one solution.
Also for any \(v, \bar{v}, x, \bar{x}\in \mathbf{R}\), we have
Hence \((H_{2})\) satisfied with \(L=\frac{1}{130e^{20}}\).
And for any \(\theta , \bar{\theta }\in \operatorname{PC}(J,\mathbf{R})\), \(t\in J\), we have
Similarly
The last two inequalities imply that \(m=\frac{1}{25}\) and \(l= \frac{1}{50}\) and hence \((H_{3})\) and \((H_{4})\) are satisfied as well. To find δ, we have \(\delta =1-\eta =1-\frac{1}{5}=\frac{4}{5}\). For these values of L, b, m, l, λ, δ, η and q, the inequality
holds. Therefore, by Theorem 3.2, the impulsive BVP (26) has a unique solution. From the conditions of Theorem 4.3 it follows that the given IBVP (26) is UH stable and consequently GUH stable.
6 Conclusion
In this paper we have studied a class of three point BVP of nonlinear implicit FDEs with impulsive conditions. Using fixed point theory and nonlinear functional analysis, we have obtained sufficient conditions under which the given problem has at least one solution. Also in Theorem 3.2, we have obtained sufficient conditions which guarantee the uniqueness of solution of the given problem. Similarly in Theorem 4.3 and Theorem 4.4, we have derived some sufficient conditions under which the solutions of the concerned problem is UH stable and UHR stable, respectively. In the last section we have given two numerical examples to verify our results.
Abbreviations
- FDEs, IBVP, BVP, UH:
-
stability
- GUH:
-
stability
- GUHR:
-
stability
References
Abbas, S., Benchohra, M., N’Guerekata, G.M.: Advanced Fractional Differential and Integral Equations. Nova Science Publishers, New York (2015)
Abbas, S., Benchohra, M., N’Guerekata, G.M.N.: Topics in Fractional Differential Equations. Springer, Berlin (2012)
Agarwal, P., Al-Mdallal, Q., Cho, Y.J., Jain, S.: Fractional differential equations for the generalized Mittag–Leffler function. Adv. Differ. Equ. 2018, 58 (2018)
Agarwal, P., Choi, J.: Fractional calculus operators and their image formulas. J. Korean Math. Soc. 53, 1183–1210 (2016)
Agarwal, P., Choi, J., Paris, R.B.: Extended Riemann–Liouville fractional derivative operator and its applications. J. Nonlinear Sci. Appl. 8, 451–466 (2015)
Agarwal, P., Dragomir, S.S., Jleli, M., Samet, B.: Advances in Mathematical Inequalities and Applications (Trends in Mathematics) (2019)
Agarwal, P., Jleli, M., Samet, B.: Fixed Point Theory in Metric Spaces. Recent Advances and Applications (2018)
Agarwal, R.P., Belmekki, M., Benchohra, M.: A survey on semilinear differential equations and inclusions involving Riemann-Liouville fractional derivative. Adv. Differ. Equ. 2009, 981728 (2009)
Agarwal, R.P., Benchohra, M., Hamani, S.: A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Appl. Math. 109, 973–1033 (2010)
Ali, A., Rabiei, F., Shah, K.: On Ulam’s type stability for a class of impulsive fractional differential equations with nonlinear integral boundary conditions. J. Nonlinear Sci. Appl. 10, 4760–4775 (2017)
Anastassiou, G.A.: Advances on Fractional Inequalities. Springer, New York (2011)
Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus Models and Numerical Methods. World Scientific, New York (2012)
Baleanu, D., Guvenc, Z.B., Machado, J.A.T.: New Trends in Nanotechnology and Fractional Calculus Applications. Springer, New York (2010)
Benchohra, M., Lazreg, J.E.: Nonlinear fractional implicit differential equations. Commun. Appl. Anal. 17, 471–482 (2013)
Benchohra, M., Lazreg, J.E.: Existence results for nonlinear implicit fractional deferential equations with impulses. Commun. Appl. Anal. 19, 413–426 (2015)
Fečkan, M., Wang, J.: A general class of impulsive evolution equations. Topol. Methods Nonlinear Anal. 46, 915–933 (2015)
Granas, A., Dugundji, J.: Fixed Point Theory. Springer, New York (2003)
Hyers, D.H.: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 27, 222–224 (1941)
Jung, S.M.: On the Hyers–Ulam stability of the functional equations that have the quadratic property. J. Math. Anal. Appl. 222, 126–137 (1998)
Jung, S.M.: Hyers–Ulam stability of linear differential equations of first order. Appl. Math. Lett. 19, 854–858 (2006)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier, Amsterdam (2006)
Kiymaz, I.O., Cetinkaya, A., Agarwal, P.: An extension of Caputo fractional derivative operator and its applications. J. Nonlinear Sci. Appl. 9, 3611–3621 (2016)
Machado, J.T., Kiryakova, V., Mainardi, F.: Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. (2010)
Obloza, M.: Hyers stability of the linear differential equation. Rocznik Nauk.-Dydakt. Prace Mat. 13, 259–270 (1993)
Otigueira, M.D.: Fractional Calculus for Scientists and Engineers. Lecture Notes in Electrical Engineering. Springer, Dordrecht (2011)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Rogovchenko, Y.V.: Impulsive evolution systems: main results and new trends. Dyn. Contin. Discrete Impuls. Syst. 3, 57–88 (1997)
Rus, I.A.: Ulam stabilities of ordinary differential equations in a Banach space. Carpath. J. Math. 26, 103–107 (2010)
Ruzhansky, M., Cho, Y.J., Agarwal, P., Area, I.: Advances in Real and Complex Analysis with Applications. Springer, Singapore (2017)
Shah, K., Ali, A., Bushnaq, S.: Hyers–Ulam stability analysis to implicit Cauchy problem of fractional differential equations with impulsive conditions. Math. Methods Appl. Sci. 41, 1–15 (2018)
Shah, K., Khalil, H., Khan, R.A.: Investigation of positive solution to a coupled system of impulsive boundary value problems for nonlinear fractional order differential equations. Chaos Solitons Fractals 77, 240–246 (2015)
Sun, J.X.: Nonlinear Functional Analysis and Its Application. Science Press, Beijing (2008)
Ulam, S.M.: Problems in Modern Mathematics. Wiley, New York (1940)
Ulam, S.M.: A Collection of Mathematical Problems. Interscience, New York (1960)
Wang, G., Zhang, L., Song, G.: Extremal solutions for the first order impulsive functional differential equations with upper and lower solutions in reversed order. J. Comput. Appl. Math. 235, 325–333 (2010)
Wang, J.R., Fečkan, M., Tian, Y.: Stability analysis for a general class of non-instantaneous impulsive differential equations. Mediterr. J. Math. 14, 1–21 (2017)
Wang, J.R., Fečkan, M., Zhou, Y.: Fractional order differential switched systems with coupled nonlocal initial and impulsive conditions. Bull. Sci. Math. 141, 727–746 (2017)
Wang, J.R., Xuezhu, L.: A uniform method to Ulam–Hyers stability for some linear fractional equations. Mediterr. J. Math. 13, 625–635 (2016)
Zavalishchin, S.T., Sesekin, A.N.: Dynamic Impulse Systems. Theory and Applications. Kluwer Academic, Dordrecht (1997)
Zhang, S.: Positive solutions for boundary value problem of nonlinear fractional differential equations. Electron. J. Differ. Equ. 2006, 36 (2006)
Zhang, X., Agarwal, P., Liu, Z., Peng, H.: The general solution for impulsive differential equations with Riemann–Liouville fractional-order \(q\in (1, 2)\). Open Mathematics 13 (2015)
Acknowledgements
We are very thankful to the anonymous referees for their useful corrections.
Funding
This research work has been financially supported by Higher Education Commission (HEC) of Pakistan under the grant number 21-1657/SRGP/R&D/HEC/2017.
Author information
Authors and Affiliations
Contributions
All authors have equal contribution in this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
There does not exist any competing interest regarding this manuscript.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Asma, Ali, A., Shah, K. et al. Ulam–Hyers stability analysis to a class of nonlinear implicit impulsive fractional differential equations with three point boundary conditions. Adv Differ Equ 2019, 7 (2019). https://doi.org/10.1186/s13662-018-1943-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1943-x
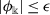 ,
,  ,
,  ;
;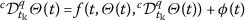 ,
,  ,
, 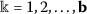 ;
; ,
, 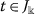 ,
, 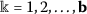 ;
;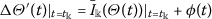 ,
, 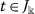 ,
, 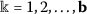 .
.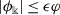 ,
, 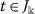 ,
, 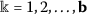 ;
;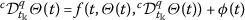 ,
, 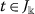 ,
, 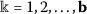 ;
; ,
, 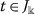 ,
, 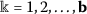 ;
;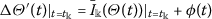 ,
, 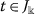 ,
, 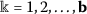 .
.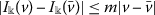 ;
;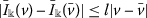 .
.