- Research
- Open access
- Published:
Existence and stability analysis to a coupled system of implicit type impulsive boundary value problems of fractional-order differential equations
Advances in Difference Equations volume 2019, Article number: 101 (2019)
Abstract
In this paper, we study a coupled system of implicit impulsive boundary value problems (IBVPs) of fractional differential equations (FODEs). We use the Schaefer fixed point and Banach contraction theorems to obtain conditions for the existence and uniqueness of positive solutions. We discuss Hyers–Ulam (HU) type stability of the concerned solutions and provide an example for illustration of the obtained results.
1 Introduction
The fractional calculus is one of the most emerging areas of investigation. The fractional differential operators are used to model many physical phenomena in a much better form as compared to ordinary differential operators, which are local. Results derived by FDEs are much better and more accurate. For applications and details on fractional calculus, we refer the readers to [1,2,3,4,5,6,7]. Our work is concerned with implicit-type coupled systems of FODEs with impulsive conditions. The IFODEs are of high worth. Such equations arise in management sciences, business mathematics and other managerial sciences, and so on. Some physical phenomena have sudden changes and discontinuous jumps. To model such problems, we impose impulsive conditions on the differential equations at discontinuity points. For applications and recent work, we refer the readers to [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Coupled systems of FODEs have been studied extensively in the last few decades because in applied sciences, we deal with many physical problems that can be modeled via these systems. We would like to refer the readers to [30,31,32,33,34,35,36] and references therein.
Since in many situations, such as nonlinear analysis and optimization, finding the exact solution of differential equations is almost difficult or impossible, we consider approximate solutions. It is important to note that only stable approximate solutions are acceptable. Various approaches of stability analysis are adopted for this purpose. The HU-type stability concept has been considered in the numerous literature. The said stability analysis is an easy and simple way in this regard. This type concept of stability was formulated for the first time by Ulam [37], and then the next year it was elaborated by Hyers [38]. In the beginning, this concept was applied to ordinary differential equations and then extended to FODEs. We refer the readers to [39,40,41,42,43,44]. Very recently, Ali et al. [45], studied the Ulam-type stability for coupled systems of nonlinear implicit fractional differential equations.
Motivated by the aforesaid work, in this paper, we investigate the following coupled system with impulsive and \((m+2)\)-point boundary conditions:
where \(1<\alpha ,\beta \leq 2\), Φ, \(\varPsi :[0,1]\times \mathrm{R} \times \mathrm{R}\rightarrow \mathrm{R}\), and \(g, h; f, \kappa : C( \mathrm{J}, \mathrm{R})\rightarrow \mathrm{R}\) are continuous functions defined as
\(\xi _{i},\eta _{i},\xi _{j},\eta _{j} \in (0,1) \) for \(i=1,2,\ldots, \mathbf{q}\), \(j=1,2,\ldots,\mathbf{p}\), and
The notations \(\xi (t_{j}^{+})\), \(\mu (t_{i}^{+})\) are right limits, and \(\xi (t_{j}^{-})\), \(\mu (t_{i}^{-})\) are left limits; \(I_{j},\bar{I} _{j},I_{i},\bar{I}_{i} :\mathrm{R}\rightarrow \mathrm{R}\) are continuous functions; and \(\mathrm{D}_{0+}^{\alpha }\), \(\mathrm{D}_{0+}^{\beta }\) are the Caputo-type fractional differential operators of order α and β, respectively.
For system (1), we discuss necessary and sufficient conditions for the existence and uniqueness of a positive solution by using the Schaefer fixed point and Banach contraction theorems. Further, we investigate various kinds of HU and GHU stability.
2 Background materials and some auxiliary results
In this section, we give some basic definitions and results, which are used in the proof of our results.
We define the spaces of all piecewise continuous functions
Clearly, \(\mathrm{B}_{1}\) and \(\mathrm{B}_{2}\) are Banach spaces under the norms \(\|\xi \|_{\mathrm{B}_{1}}=\max_{t\in \mathrm{J}}|\xi (t)|\) and \(\|\mu \|_{\mathrm{B}_{2}}=\max_{t\in \mathrm{J}}|\mu (t)|\), respectively. Their product \(\mathbf{B}=\mathrm{B}_{1}\times \mathrm{B}_{2}\) is also a Banach space with norm \(\|(\xi ,\mu )\|_{\mathbf{B}}=\|\xi \|_{\mathrm{B}_{1}}+\|\mu \|_{\mathrm{B}_{2}}\).
Definition 1
([1])
The Caputo fractional derivative of a function \(\xi :(0, \infty )\rightarrow \mathrm{R}\) is defined by
where \(l=[\alpha ]+1\), and \([\alpha ]\) denotes the integer part of a real number α.
Definition 2
([4])
The Riemann–Liouville fractional integral of order \(\alpha \in \mathbb{R_{+}}\) of a function \(\xi \in C ((0,\infty ),\mathrm{R} )\) is defined as
where \(\alpha >0\), and Γ is the gamma function, provided that the right-hand side is pointwise defined on \((0,\infty )\).
Lemma 1
([46])
For \(\alpha >0\), we have
Lemma 2
([46])
For \(\alpha >0\), the differential equation \({^{C} \mathrm{D}_{t}^{\alpha }} \xi (t)=x(t)\) has the following solution:
where \(l=[\alpha ]+1\).
Theorem 1
(Schaefer’s fixed point theorem [47])
Let \(\mathfrak{B}\) be a Banach space, and let \(\mathscr{T} : \mathfrak{B}\rightarrow \mathfrak{B}\) be a completely continuous operator. If the set \(\mathrm{W} = \{\xi \in \mathfrak{B} :\ \xi = \eta \mathscr{T}\xi ,\ 0< \eta <1\}\) is bounded, then \(\mathscr{T}\) has a fixed point in \(\mathfrak{B}\).
Definition 3
([48])
The coupled system (1) is said to be HU stable if there exists \(\mathbf{K}_{\alpha ,\beta }=\max \{\mathbf{K}_{\alpha }, \mathbf{K}_{\beta }\}>0\) such that, for \(\epsilon =\max \{ \epsilon _{\alpha },\epsilon _{\beta }\}>0\) and for every solution \((\xi ,\mu )\in \mathbf{B}\) of the inequality
there exists a unique solution \((\vartheta ,\sigma )\in \mathbf{B}\) with
Definition 4
([48])
The coupled system (1) is said to be GHU stable if there exists \(\varphi \in \mathcal{C}(\mathrm{R}^{+},\mathrm{R}^{+})\) with \(\varphi (0)=0\) such that, for any approximate solution \((\xi ,\mu )\in \mathbf{B}\) of inequality (2), there exists a unique solution \((\vartheta ,\sigma )\in \mathbf{B}\) of (1) satisfying
Denote \(\varPhi _{\alpha ,\beta }=\max \{\varPhi _{\alpha },\varPhi _{\beta }\} \in \mathcal{C}(\mathrm{J},\mathrm{R})>0\) and \(\mathbf{K}_{\varPhi _{ \alpha },\varPhi _{\beta }}=\max \{\mathbf{K}_{\varPhi _{\alpha }},\mathbf{K} _{\varPhi _{\alpha }}\}>0\).
Definition 5
([48])
The coupled system (1) is said to be HU-Rassias stable with respect to \(\varPhi _{\alpha ,\beta }\) if there exists a constant \(\mathbf{K}_{\varPhi _{\alpha },\varPhi _{\beta }}\) such that, for some \(\epsilon >0\) and for any approximate solution \((\xi ,\mu )\in \mathbf{B}\) of the inequalities
there exists a unique solution \((\vartheta ,\sigma )\in \mathbf{B}\) with
Definition 6
([48])
The coupled system (1) is said to be GHU-Rassias stable with respect to \(\varPhi _{\alpha ,\beta }\) if there exists a constant \(\mathbf{K}_{\varPhi _{\alpha },\varPhi _{\beta }}\) such that, for any approximate solution \((\xi ,\mu )\in \mathbf{B}\) of inequality (5), there exists a unique solution \((\vartheta ,\sigma ) \in \mathbf{B}\) of (1) satisfying
Remark 1
We say that \((\xi ,\mu )\in \mathbf{B}\) is a solution of the system of inequalities (2) if there exist functions \(\varTheta ,\theta \in \mathcal{C}(\mathrm{J},\mathrm{R})\) depending upon ξ, μ, respectively, such that
-
(i)
\(|\varTheta (t) |\leq \epsilon _{\alpha }\), \(| \theta (t) |\leq \epsilon _{\beta }\), \(t\in \mathrm{J}\);
-
(ii)
and
$$ \textstyle\begin{cases} {}_{0}^{C}\mathrm{D}_{t_{j}}^{\alpha } \xi (t)=\varPhi (t,\mu (t),{}_{0} ^{C} \mathrm{D}_{t_{j}}^{\alpha }\xi (t) )+\varTheta (t), \quad t\in\mathrm{J}, \\ \Delta \xi (t_{j})=I_{j} (\xi (t_{j}) )+\varTheta _{j}, \\ \Delta \xi '(t_{j})=\bar{I}_{j} (\xi (t_{j}) )+\varTheta _{j}, \\ {}_{0}^{C}\mathrm{D}_{t_{i}}^{\beta }\mu (t)= \varPsi (t,\xi (t),{}_{0}^{C} \mathrm{D}_{t_{i}}^{\beta } \mu (t) )+\theta (t),\quad t\in \mathrm{J}, \\ \Delta \mu (t_{i})=I_{i} (\mu (t_{i}) )+\theta _{i}, \\ \Delta \mu '(t_{i})=\bar{I}_{i} (\mu (t_{i}) )+\theta _{i}. \end{cases} $$
3 Main results
In this section, we present our main results.
Theorem 2
The solution \((\xi ,\mu )\in \mathbf{B}\) of the coupled system
is given by the integral equations
Proof
The proof can be obtained as in [14, 34]. □
Corollary 1
In view of Theorem 2, our coupled system (1) has the following solution:
For simplicity, we use use the notations \(u_{\mu ,\xi }(t)=\varPhi (t, \mu (t),{}_{0}^{C}\mathrm{D}_{t_{j}}^{\beta }\xi (t))\) and \(v_{\xi , \mu }(t)=\varPhi (t,\xi (t),{}_{0}^{C}\mathrm{D}_{t_{i}}^{\beta }\mu (t))\). To convert the considered problem into a fixed point problem, we define the operator \(T:\mathbf{B}\rightarrow \mathbf{B}\) by such that
We obtain our results under the following assumptions:
- \((H_{1})\) :
-
for any \(\xi ,\mu \in C([0,1],\mathrm{R})\), there exist \(K_{g},K_{h},K_{f},K_{\kappa }>0\) such that
$$\begin{aligned}& \bigl\Vert g(\xi )-g(\mu ) \bigr\Vert _{PC}\leq K_{g} \Vert \xi -\mu \Vert _{PC}, \qquad \bigl\Vert f(\xi )-f(\mu ) \bigr\Vert _{PC}\leq K_{f} \Vert \xi -\mu \Vert _{PC}, \\& \bigl\Vert h(\xi )-h(\mu ) \bigr\Vert _{PC}\leq K_{h} \Vert \xi -\mu \Vert _{PC}, \qquad \bigl\Vert \kappa (\xi )-\kappa ( \mu ) \bigr\Vert _{PC}\leq K_{\kappa } \Vert \xi -\mu \Vert _{PC}; \end{aligned}$$ - \((H_{2})\) :
-
for all \(\xi ,\bar{\xi },\mu ,\bar{\mu }\in \mathrm{R}\) and \(t\in [0,1]\) there exist \({L_{\varPhi }}_{1}>0\), \(0<{L_{ \varPhi }}_{2}<1\), \({L_{\varPsi }}_{1}>0\), and \(0<{L_{\varPsi }}_{2}<1 \) such that
$$\begin{aligned}& \bigl\vert \varPhi (t,\xi ,\mu )-\varPhi (t,\bar{\xi },\bar{\mu }) \bigr\vert \leq {L_{\varPhi }} _{1} \vert \xi -\bar{\xi } \vert +{L_{\varPhi }}_{2} \vert \mu -\bar{\mu } \vert , \\& \bigl\vert \varPsi (t,\xi ,\mu )-\varPsi (t,\bar{\xi },\bar{\mu }) \bigr\vert \leq {L_{\varPsi }} _{1} \vert \xi -\bar{\xi } \vert +{L_{\varPsi }}_{2} \vert \mu -\bar{\mu } \vert ; \end{aligned}$$ - \((H_{3})\) :
-
there exist constants \(A_{1}\), \(A_{2}\), \(A_{3}\) and \(A_{4}>0\) such that, for \(\xi ,\bar{\xi }, \mu , \bar{\mu } \in \mathrm{R}\),
$$\begin{aligned}& \bigl\vert I_{j}(\xi )-I_{j}(\bar{\xi }) \bigr\vert \leq A_{1} \vert \xi -\bar{\xi } \vert ,\qquad \bigl\vert \bar{I} _{j}(\xi )-\bar{I}_{j}(\bar{\xi } \bigr\vert \leq A_{2} \vert \xi -\bar{\xi } \vert ,\quad j=1,2,\ldots,m, \\& \bigl\vert I_{i}(\mu )-I_{i}(\bar{\mu }) \bigr\vert \leq A_{3} \vert \mu -\bar{\mu } \vert ,\qquad \bigl\vert \bar{I} _{i}(\mu )-\bar{I}_{i}(\bar{\mu } \bigr\vert \leq A_{4} \vert \mu -\bar{\mu } \vert ,\quad i=1,2,\ldots,n; \end{aligned}$$ - \((H_{4})\) :
-
there exist constants
 such that
such that

and
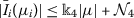 , \(i=1,2,\ldots,n\);
, \(i=1,2,\ldots,n\); - \((H_{5})\) :
-
there exist constants
 ,
, 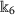 ,
,  ,
,  such that
such that

for all \(\mu \in C([0,1],\mathrm{R})\);
- \((H_{6})\) :
-
there exist some functions \(p_{1}\), \(q_{1}\), \(r_{1}\) and \(p_{2},q_{2},r_{2} \in C(\mathrm{J},\mathrm{R}^{+})\) such that, for \(t\in \mathrm{J}\) and \((\mu ,\xi )\in \mathbf{B}\), we have
$$ \bigl\vert \varPhi \bigl(t,\mu (t),{}_{0}^{C} \mathrm{D}_{t_{j}}^{\alpha }\xi (t) \bigr) \bigr\vert \leq p _{1}(t)+q_{1}(t) \vert \mu \vert +r_{1}(t) \bigl\vert {}_{0}^{C}\mathrm{D}_{t_{j}}^{\alpha } \xi (t) \bigr\vert $$with \({p_{1}}^{*}=\sup_{t\in \mathrm{J}}|p_{1}(t)|\), \({q_{1}}^{*}= \sup_{t\in \mathrm{J}}|q_{1}(t)|\), and \({r_{1}}^{*}=\sup_{t\in \mathrm{J}}|r_{1}(t)|<1 \) and
$$ \bigl\vert \varPsi \bigl(t,\xi (t),{}_{0}^{C} \mathrm{D}_{t_{j}}^{\alpha }\mu (t) \bigr) \bigr\vert \leq p _{2}(t)+q_{2}(t) \vert \mu \vert +r_{2}(t) \bigl\vert {}_{0}^{C}\mathrm{D}_{t_{j}}^{\alpha } \xi (t) \bigr\vert , $$with \({p_{2}}^{*}=\sup_{t\in \mathrm{J}}|p_{2}(t)|\), \({q_{2}}^{*}= \sup_{t\in \mathrm{J}}|q_{2}(t)|\), and \({r_{2}}^{*}=\sup_{t\in \mathrm{J}}|r_{2}(t)|<1\).
Theorem 3
If assumptions \((H_{1})\), \((H_{2})\), \((H_{3})\) and the inequality
are satisfied, where
and
then the coupled system (1) has a unique solution.
Proof
Take \((\xi ,\mu ), (\bar{\xi },\bar{\mu })\in \mathbf{B}\) and consider
which further means that
By assumption \((H_{2})\) we have
By assumptions \((H_{1})\) and \((H_{3})\) and inequality (14), taking the maximum over the interval J, from inequality (13) we have
where
Similarly, we have
where
from which we have
where \(\aleph =\max \{\aleph _{1},\aleph _{2}\}\). Hence T is a contraction, and therefore, by the Banach contraction principle, T has a unique fixed point. □
Theorem 4
If assumptions \((H_{1})\)–\((H_{6})\) hold, then the coupled system (1) has at least one solution.
Proof
Here we use the Schaefer fixed point theorem. We need to show that the operator T has at least one fixed point. There are several steps involved in this method.
Step 1: We will show that the operator T is continuous. Take a sequence \((\xi _{n},\mu _{n})\rightarrow (\xi ,\mu )\in \mathbf{B}\). For any \(t\in \mathrm{J}\), we consider
By assumption \((H_{2})\) we have
Since \(\mu _{n}\rightarrow \mu \) as \(n\rightarrow \infty \), we have that, for each \(t\in \mathrm{J}\), \(u_{\mu ,\xi ,n}(t)\rightarrow u_{\mu , \xi }(t)\) as \(n\rightarrow \infty \). Also, for each \(t\in \mathrm{J}\), \(\xi _{n}(t)\rightarrow \xi (t)\) as \(n\rightarrow \infty \). Since every convergent sequence is bounded, there exists a constant b such that \(|u_{\mu ,\xi ,n}(t)|\leq \mathbf{b}\) and \(|u_{\mu ,\xi }(t)| \leq \mathbf{b}\) for each \(t\in \mathrm{J}\). We have
Clearly, the functions \(s\rightarrow 2\mathbf{b}(t-s)^{\alpha -1}\), \(s\rightarrow 2\mathbf{b}(t_{j}-s)^{\alpha -1}\), and \(s\rightarrow 2 \mathbf{b}(t_{j}-s)^{\alpha -2}\) are integrable on the interval [0, t]. Thus, by assumptions \((H_{1})\)–\((H_{3})\), inequality (16), and the Lebesgue dominated convergence theorem, the right-hand side of inequality (15) goes to zero, that is,
and thus
This implies that the operator \(T_{\alpha }\) is continuous. Similarly, we can show that the operator \(T_{\beta }\) is continuous, so that the operator is continuous.
Step 2: We define the set \(\varOmega _{\varrho }=\{(\xi , \mu )\in \mathbf{B}:|(\xi ,\mu )|\leq \varrho \mbox{ with } |\xi |\leq \varrho _{1} \mbox{ and } |\mu |\leq \varrho _{2}\}\), where \(\max \{\varrho _{1}, \varrho _{2}\}=\varrho \). For \(t\in \mathrm{J}\), we consider
By \((H_{6})\) we have
Thus by \((H_{4})\), \((H_{5})\), and \((H_{6})\) from (17) we obtain the following result:

Similarly, we can show that
Now if \(\max (\varsigma _{1},\varsigma _{2})=\varsigma \), then we have
This shows that bounded sets are mapped into bounded sets under T.
Step 3: W will show that T is equicontinuous. Let \(\mathbb{D}\subseteq \mathbf{B}\). Then for \((\xi , \mu )\in \mathbb{D}\) and \(t_{1},t_{2}\in \mathrm{J}\) such that \(t_{1}< t_{2}\), we consider
We can see that the right-hand side of inequality (21) approaches to zero as \(t_{1}\rightarrow t_{2}\). Hence
Similarly, we can show that
Therefore by the Ascoli–Arzelà theorem the operators \(T_{\alpha }\), \(T_{\beta }\) are completely continuous, and consequently T is completely continuous.
Step 4: Define the set \(\mathcal{Z}=\{(\xi , \mu )\in \mathbf{B}:(\xi ,\mu )=\delta T(\xi ,\mu ), 0<\delta <1\}\). We will show that \(\mathcal{Z}\) is bounded. If \((\xi ,\mu )\in \mathcal{Z}\), then by definition \((\xi ,\mu )=\delta T(\xi ,\mu )\). Hence for any \(t\in \mathrm{J}\), we can write
Taking the absolute values of both sides of (22) and using \(0<\delta <1\), we have
From inequalities (18) and (19) we have

Similarly, we can obtain
where \(\varsigma =\max (\varsigma _{1},\varsigma _{2})\). Thus the set \(\mathcal{S}\) is bounded, and hence, by the Schaefer fixed point Theorem, T has at least one fixed point. Consequently, the considered coupled system (1) has at least one solution. □
4 Stability analysis
Theorem 5
If assumptions \((H_{1})\)–\((H_{3})\) and inequalities (11) are satisfied and if \(\varpi =1-\frac{\aleph _{1}\aleph _{2}}{(1-\aleph _{1})(1- \aleph _{2})}>0\), then the unique solution of the coupled system (1) is HU stable and consequently GHU stable.
Proof
Let \((\xi ,\mu )\in \varLambda \) be an approximate solution of inequality (2), and let \((\vartheta ,\sigma )\in \varLambda \) be the unique solution of the coupled system given by
By Remark 1 we have
By Corollary 1 the solution of problem (27) is
We consider
As in Theorem 3, we get
and
and
respectively. Let \(\frac{2(4m+1)}{1-\aleph _{1}}=\mathbf{C}_{\alpha }\) and \(\frac{2(4n+1)}{1-\aleph _{2}}=\mathbf{C}_{\beta }\). Then the last two inequalities can be written in matrix form as
which yields
where
From system (31) we have
which imply that
If \(\max \{\epsilon _{\alpha },\epsilon _{\beta }\}=\epsilon \) and \(\frac{\mathbf{C}_{\alpha }}{\varpi }+\frac{\mathbf{C}_{\beta }}{ \varpi }+\frac{\aleph _{1}\mathbf{C}_{\beta }}{\varpi (1-\aleph _{1})}+\frac{ \aleph _{2}\mathbf{C}_{\alpha }}{\varpi (1-\aleph _{2})}=\mathbf{C}_{ \alpha ,\beta }\), then
This shows that system (1) is HU stable. Also, if
with \(\varphi (0)=0\), then the solution of system (1) is GHU stable. □
For the next result, we assume that
- \((H_{7})\) :
-
There exist two nondecreasing functions \(\gamma _{ \alpha },\gamma _{\beta }\in C(\mathrm{J},\mathrm{R}^{+})\) such that
$$ {}_{0}\mathrm{I}_{t}^{\alpha }\gamma _{\alpha }(t) \leq \mathcal{L}_{1} \gamma _{\alpha }(t) \quad \mbox{and}\quad {}_{0}\mathrm{I}_{t}^{\beta }\gamma _{\beta }(t)\leq \mathcal{L}_{2} \gamma _{\beta }(t),\quad \mbox{where } \mathcal{L}_{1},\mathcal{L}_{2}>0. $$
Theorem 6
If assumptions \((H_{1})\)–\((H_{3})\) and \((H_{7})\) and inequalities (11) are satisfied and if \(\varpi =1-\frac{\aleph _{1}\aleph _{2}}{(1-\aleph _{1})(1-\aleph _{2})}>0\), then the unique solution of the coupled system (1) is HU-Rassias stable, and consequently it is GHU-Rassias stable.
Proof
We can obtain the result by using Definition 5 and performing the same procedure as in Theorem 5. □
5 Example
To testify our results established in the previous section, we provide an adequate problem.
Example 1
In system (32), we see that \(\alpha =\beta =\frac{3}{2}\), and \(t_{j}\neq \frac{1}{4}\) for \(j=1,2,\dots ,50\). For \(t\in [0,1]\) and \(\xi ,\bar{\xi },\mu ,\bar{\mu }\in \mathrm{R}\), we obtain
and
From this we get \({L_{\varPhi }}_{1}={L_{\varPhi }}_{2}=\frac{1}{40}\) and \({L_{\varPsi }}_{1}={L_{\varPsi }}_{2}=\frac{1}{30}\). Also,
From this we obtain that \(K_{g}=\frac{1}{75}\), \(K_{h}=\frac{1}{25}\), \(K_{f}= \frac{1}{90}\), \(K_{\kappa }=\frac{1}{45}\), \(A_{1}=\frac{1}{60}\), \(A_{2}= \frac{1}{120}\), \(A_{3}=\frac{1}{40}\), \(A_{4}=\frac{1}{80}\), and \(m=1\). Calculating
and
we have \(\aleph _{1}=0.407<1\) and \(\aleph _{2}=0.467<1\), that is, \(\max (\aleph _{1},\aleph _{2})<1\). Therefore by Theorem 3 the coupled system (32) has a unique solution. Also, \(\varpi =1-\frac{ \aleph _{1}\aleph _{2}}{(1-\aleph _{1})(1-\aleph _{2})}=0.8096104>0\), and hence by Theorem 5 the coupled system (32) is HU stable and thus GHU stable. Similarly, we can verify the conditions of Theorems 6 and 4. Next, we take the initial values for the required solution \(\xi =1\), \(\mu =2\), and at the given fractional order the stability graph is given in Fig. 1 corresponding to the parametric values computed.
Graphical representation of HU-stability results for Example 1
6 Conclusion
We successfully applied the Schaefer and Banach fixed point theorems to develop sufficient conditions for the existence of at least one solution and its uniqueness, respectively. Then we obtained some results for different kinds of HU stability. The whole analysis was demonstrated by an example.
Abbreviations
- IBVP:
-
implicit boundary value problem
- FODEs:
-
fractional-order differential equations
- IFODEs:
-
implicit fractional-order differential equations
- HU:
-
Hyers Ulam
- GHU:
-
generalized Hyers Ulam
- GHUR:
-
generalized Hyers Ulam Rassias
References
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier, Amsterdam (2006)
Kilbas, A.A., Marichev, O.I., Samko, S.G.: Fractional Integrals and Derivatives (Theory and Applications). Gordon and Breach, Switzerland (1993)
Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1993)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Rossikhin, Y.A., Shitikova, M.V.: Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 50, 15–67 (1997)
Agarwal, R.P., Asma, Lupulescu, V., O’Regan, D.: Fractional semilinear equations with causal operators. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111, 257–269 (2017)
Ali, A., Rabieib, F., Shah, K.: On Ulam’s type stability for a class of impulsive fractional differential equations with nonlinear integral boundary conditions. J. Nonlinear Sci. Appl. 10, 4760–4775 (2017)
Shah, K., Ali, A., Bushnaq, S.: Hyers–Ulam stability analysis to implicit Cauchy problem of fractional differential equations with impulsive conditions. Math. Methods Appl. Sci. 41, 1–15 (2018)
Ali, A., Shah, K., Baleanu, D.: Ulam stability results to a class of nonlinear implicit boundary value problems of impulsive fractional differential equations. Adv. Differ. Equ. 2019(5), 1 (2019)
Asma, Ali, A., Shah, K., Jarad, F.: Ulam–Hyers stability analysis to a class of nonlinear implicit impulsive fractional differential equations with three point boundary conditions. Adv. Differ. Equ. 2019(7), 1 (2019)
Wang, J., Zhou, Y., Fec, M.: Nonlinear impulsive problems for fractional differential equations and Ulam stability. Comput. Math. Appl. 64(10), 3389–3405 (2012)
Wang, J., Feckan, M., Tian, Y.: Stability analysis for a general class of non-instantaneous impulsive differential equations. Mediterr. J. Math. 14(2), 1–21 (2017)
Yang, D., Wang, J., O’Regan, D.: On the orbital Hausdorff dependence of differential equations with non-instantaneous impulses. C. R. Acad. Sci. Paris, Ser. I 356(2), 150–171 (2018)
Wang, J., Feckan, M., Zhou, Y.: Fractional order differential switched systems with coupled nonlocal initial and impulsive conditions. Bull. Sci. Math. 141(7), 727–746 (2017)
Andronov, A., Witt, A., Haykin, S.: Oscillation Theory. Nauka, Moskow (1981)
Babitskii, V., Krupenin, V.: Vibration in Strongly Nonlinear Systems. Nauka, Moskow (1985)
Chua, L.O., Yang, L.: Cellular neural networks: applications. IEEE Trans. Circuits Syst. 35, 1273–1290 (1988)
Chernousko, F., Akulenko, L., Sokolov, B.: Control of Oscillations. Nauka, Moskow (1980)
Popov, E.: The Dynamics of Automatic Control Systems. Gostehizdat, Moskow (1964)
Zavalishchin, S., Sesekin, A.: Impulsive Processes: Models and Applications. Nauka, Moskow (1991)
Abdeljawad, T., Jarad, F., Baleanu, D.: On the existence and the uniqueness theorem for fractional differential equations with bounded delay within Caputo derivatives. Sci. China Ser. A, Math. 51(10), 1775–1786 (2008)
Abdeljawad (Maraaba), T., Baleanu, D., Jarad, F.: Existence and uniqueness theorem for a class of delay differential equations with left and right Caputo fractional derivatives. J. Math. Phys. 49(8) (2008)
Alzabut, J., Abdeljawad, T.: A generalized discrete fractional Gronwall inequality and its application on the uniqueness of solution and its application on the uniqueness of solutions for nonlinear delay fractional difference system. Appl. Anal. Discrete Math. 12, 036 (2018)
Abdeljawad, T., Alzabut, J., Baleanu, D.: A generalized q-fractional Gronwall inequality and its applications to nonlinear delay q-fractional difference systems. J. Inequal. Appl. 2016, 240 (2016)
Abdeljawad, T.: A Lyapunov type inequality for fractional operators with nonsingular Mittag-Leffler kernel. J. Inequal. Appl. 2017, 130 (2017)
Abdeljawad, T., Alzabut, J.: On Riemann–Liouville fractional q-difference equations and their application to retarded logistic type model. Math. Methods Appl. Sci. 41(18), 8953–8962 (2018)
Abdeljawad, T., Al-Mdallal, Q.M.: Discrete Mittag-Leffler kernel type fractional difference initial value problems and Gronwall’s inequality. J. Comput. Appl. Math. 339, 218–230 (2018)
Alzabut, J., Abdeljawad, T., Baleanu, D.: Nonlinear delay fractional difference equations with application on discrete fractional Lotka–Volterra model. J. Comput. Anal. Appl. 25(5), 889–898 (2018)
Shah, K., Wang, J., Khalil, H., Khan, R.A.: Existence and numerical solutions of a coupled system of integral BVP for fractional differential equations. Adv. Differ. Equ. 2018, 149 (2018)
Ahmad, B., Nieto, J.J.: Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions. Comput. Math. Appl. 58, 1838–1843 (2009)
Shah, K., Khan, R.A.: Existence and uniqueness of positive solutions to a coupled system of nonlinear fractional order differential equations with anti periodic boundary conditions. Differ. Equ. Appl. 7(2), 245–262 (2015)
Shah, K., Khan, R.A.: Multiple positive solutions to a coupled systems of nonlinear fractional differential equations. SpringerPlus 5(1), 1–20 (2016)
Shah, K., Khalil, H., Khan, R.A.: Investigation of positive solution to a coupled system of impulsive boundary value problems for nonlinear fractional order differential equations. Chaos Solitons Fractals 77, 240–246 (2015)
Su, X.: Boundary value problem for a coupled system of nonlinear fractional differential equations. Appl. Math. Lett. 22, 64–69 (2009)
Rehman, M., Khan, R.: A note on boundary value problems for a coupled system of fractional differential equations. Comput. Math. Appl. 61, 2630–2637 (2011)
Ulam, S.M.: A Collection of the Mathematical Problems. Interscience, New York (1960)
Hyers, D.H.: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 27(4), 222–224 (1941)
Hyers, D.H., Isac, G., Rassias, T.M.: Stability of Functional Equations in Several Variables. Birkhäuser, Boston (1998)
Ibrahim, R.W.: Generalized Ulam–Hyers stability for fractional differential equations. Int. J. Math. 23(5) (2012) 9 pages
Jung, S.M.: Hyers–Ulam stability of linear differential equations of first order. Appl. Math. Lett. 19, 854–858 (2006)
Jung, S.M.: On the Hyers–Ulam stability of functional equations that have the quadratic property. J. Math. Appl. 222, 126–137 (1998)
Li, T., Zada, A.: Connections between Hyers–Ulam stability and uniform exponential stability of discrete evolution families of bounded linear operators over Banach spaces. Adv. Differ. Equ. 2016(1), 1 (2016)
Li, T., Zada, A., Faisal, S.: Hyers–Ulam stability of nth order linear differential equations. J. Nonlinear Sci. Appl. 9, 2070–2075 (2016)
Ali, Z., Zada, A., Shah, K.: On Ulam’s Stability for a Coupled Systems of Nonlinear Implicit Fractional Differential Equations. Bull. Malays. Math. Sci. Soc. https://doi.org/10.1007/s40840-018-0625-x
Cabada, A., Wang, G.: Positive solutions of nonlinear fractional differential equations with integral boundary value conditions. J. Math. Anal. Appl. 389(1), 403–411 (2013)
Granas, A., Dugundji, J.: Fixed Point Theory. Springer, New York (2003)
Rus, I.A.: Ulam stabilities of ordinary differential equations in a Banach space. Carpath. J. Math. 26, 103–107 (2010)
Funding
The fifth author would like to thank Prince Sultan University for funding this work through research group Nonlinear Analysis Methods in Applied Mathematics (NAMAM) group number RG-DES-2017-01-17.
Author information
Authors and Affiliations
Contributions
All authors equally contributed to this paper and approved the final version.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ali, A., Shah, K., Jarad, F. et al. Existence and stability analysis to a coupled system of implicit type impulsive boundary value problems of fractional-order differential equations. Adv Differ Equ 2019, 101 (2019). https://doi.org/10.1186/s13662-019-2047-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2047-y
 such that
such that

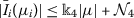 ,
,  ,
, 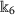 ,
,  ,
,  such that
such that

