- Research
- Open access
- Published:
A tripled fixed point technique for solving a tripled-system of integral equations and Markov process in CCbMS
Advances in Difference Equations volume 2020, Article number: 567 (2020)
Abstract
We prove the existence of tripled fixed points (TFPs) of a new generalized nonlinear contraction mapping in complete cone b-metric spaces (CCbMSs). Also, we present some exciting consequences as corollaries and three nontrivial examples. Finally, we find a solution for a tripled-system of integral equations (TSIE) and discussed a unique stationary distribution for the Markov process (SDMP).
1 Introduction and elementary discussion
Not knowing mathematics in a mathematically-driven world is like walking around a museum without looking at its walls. Learning and appreciating mathematics can help you appreciate certain things you would not otherwise focus on in your surrounding world. Mathematics is everywhere in nature. A typical example is the celebrated Fibonacci sequence of numbers, which is present in reproduction of species in nature. Mathematics is also useful to formulate epidemic models via differential or difference systems of equations that describe the couplings of the dynamics among subpopulations like susceptible, exposed, infectious, or recovered with immunity.
One of important branches of mathematics is functional analysis. The development of this field progressed in parallel to the development of modern theoretical physics. The formal framework of functional analysis adjusts closely the laws of both quantum mechanics and quantum field theory. At the same time, these physics theoretical frameworks have very relevant influence and links substantiating the body of problems and solution methodology of functional analysis.
A drop was taken from this branch and was called fixed point theory. Fixed-point technologies offer a focal concept with many diverse utilizations. It has been and still is an important theoretical tool in many fields and various disciplines such as topology, game theory, optimal control, artificial intelligence, logic programming, dynamical systems (and chaos), functional analysis, differential equations, and economics. For example, the fixed-point technique is applied to finding the solution of the equilibrium troubles in economics and game theory. In nonlinear integral equations, it used to find analytical and numerical solutions to Fredholm integral equations [1–5], and so on.
The idea of a coupled fixed point was initiated in [6]. Under this idea, some main results in partially ordered metric spaces were obtained by the same authors. For relevant properties in coupled fixed point consequences and related topics in abstract spaces, the reader can shed light from [7–21].
Pivotal results related to a TFP (established in 2011 by Berinde and Borcut [22]) were presented in partially ordered metric spaces. For more topics of this notion, we refer to [23–30].
As a generalization of ordinary metric space (OMC), a b-metric space (bMS) was presented by Bakhtin [31]. Under certain contraction conditions, he showed some important sequences in b-metric spaces. After his paper, a lot of authors discussed fixed point theory or various principles for operators (single- or multivalued) in the mentioned space as an extension of Banach’s principle in OMC; see [32–34].
Another extension of OMC, a cone metric space (CMS), was introduced by Huang and Zhang [35]. They discussed some fixed point theorems, which expanded certain results of this type to CMS.
Great papers incorporate bMS with CMS clarified by Hussain and Shah [36] under the name a cone b-metric space (CbMS), where some topological properties in such spaces and recent results about KKM mappings in a CbMS were established.
As an extension of this work, this paper was written to give some new TFPs under generalized nonlinear contraction mapping in CCbMS, We also give some important examples and corollaries to corroborate our theoretical results. Finally, we discuss contributions of TFPs to finding a solution of TSIE and a unique SDMP.
Now we present important notions of CbMS used in our paper.
Definition 1.1
([35])
Let B be a real Banach space, and let Q be a subset B. By ϑ we denote the zero element of B. The subset Q is called a cone if the following stipulations are fulfilled:
-
(i)
\(Q\neq \varnothing \) is closed, and \(Q\neq \{\vartheta \}\);
-
(ii)
\(\omega ,\hslash \in \mathbb{R} \), \(\omega ,\hslash \geq 0\), and \(p,q\in Q\Rightarrow \omega p+\hslash q\in Q \);
-
(iii)
\(Q\cap (-Q)=\{\vartheta \}\).
For a given cone \(Q\subset B\), we define a partial ordering ≾ with respect to Q by \(p\precsim q\) iff \(q-p\in Q\). We write \(p\prec q\) to indicate that \(p\precsim q\) but \(p\neq q\), whereas \(p\ll q\) stands for \(p-q\in Q^{\circ }\), where \(Q^{\circ }\) is the interior of Q.
Let \(\Vert \cdot \Vert \) be a norm on B. The cone Q is called normal if there is a number \(\Pi >0\) such that for all \(p,q\in B\), \(\vartheta \leq p\leq q\Rightarrow \Vert p \Vert \leq \Pi \Vert q \Vert \). The least positive number satisfying this inequality is called the normal constant of Q.
Definition 1.2
([35])
Let \(\chi \neq \varnothing \), and let \(\xi :\chi \times \chi \rightarrow B\) be a mapping such that for all \(p,q,r\in \chi \),
- \((c_{1})\):
-
\(\vartheta \leq \xi (p,q)\), and \(\xi (p,q)=\vartheta \Leftrightarrow p=q\);
- \((c_{2})\):
-
\(\xi (p,q)=\xi (q,p)\);
- \((c_{3})\):
-
\(\xi (p,q)\leq \xi (p,r)+\xi (r,q)\).
The pair \((\chi ,\xi )\) is called a CMS.
Definition 1.3
([36])
Let \(\chi \neq \varnothing \), and let \(s\geq 1\). A mapping \(\xi :\chi \times \chi \rightarrow B\) is called a CbM for all \(p,q,r\in \chi \) iff the following conditions are fulfilled:
- \((cb_{1})\):
-
\(\vartheta \leq \xi (p,q)\), and \(\xi (p,q)=\vartheta \Leftrightarrow p=q\);
- \((cb_{2})\):
-
\(\xi (p,q)=\xi (q,p)\);
- \((cb_{3})\):
-
\(\xi (p,q)\leq s ( \xi (p,r)+\xi (r,q) ) \).
The pair \((\chi ,\xi )\) is called a CbMS.
From these two definitions we have that any CMS is a CbMS. So the class CbMSs is larger than the class of CMSs. Here we can confirm that CbMS generalizes bMS and CMS.
We strongly refer to paper [37], which gives some important examples that show that a CbMS \((\chi ,\xi )\) is not necessarily a CMS.
Definition 1.4
([36])
Let \((\chi ,\xi )\) be a CbMS, and let \(\{p_{n}\}\) be a sequence in χ. Then for all \(p\in \chi \),
-
(1)
\(\{p_{n}\}\) converges to p if for every ε in B with \(\vartheta \ll \varepsilon \), there is \(\mathbb{N} \) such that for all \(n>\mathbb{N} \), \(\xi (p_{n},p)\ll \varepsilon \), and we write \(\lim_{n\rightarrow \infty }p_{n}=p\) or \(p_{n}\rightarrow p\) as \(n\rightarrow \infty \);
-
(2)
\(\{p_{n}\}\) is a Cauchy sequence if for every ε in B with \(\vartheta \ll \varepsilon \), there is \(\mathbb{N} \) such that \(\xi (p_{n},p_{m})\ll \varepsilon \) for all \(n,m>\mathbb{N}\);
-
(3)
the pair \((\chi ,\xi )\) is a CCbMS if every Cauchy sequence is convergent.
The following lemma is very important, especially when dealing with CMS.
Lemma 1.5
([38])
If \(\hbar \in \operatorname{int}(Y)\) and \(\vartheta \precsim p_{n} \overset{n\rightarrow \infty }{\rightarrow }\vartheta \), where Y is a cone, and \(\{p_{n}\}\) is a sequence in B, then for an arbitrary fixed N and all \(n\in N\), \(p_{n}\ll \hbar \).
Lemma 1.6
([38])
If \(p\precsim q\) and \(q\ll r\) for all \(p,q,r\in B\), then \(p\ll r\).
Lemma 1.7
([39])
Let Q be a cone. If \(\nu \in Q\) and \(\nu \leq \tau \nu \) for some \(\tau \in {}[ 0,1)\), then \(\nu =\vartheta \).
Definition 1.8
([40])
A triple \((\wp ,\hbar ,\eth )\in \chi ^{3}\) is a TFP of a self-mapping \(\Re :\chi ^{3}\rightarrow \chi \) if \(\wp =\Re (\wp ,\hbar ,\eth )\), \(\hbar =\Re (\hbar ,\wp ,\hbar )\), and \(\eth =\Re (\eth ,\hbar ,\wp )\).
Definition 1.9
([41])
Let \((\chi ,\xi )\) be a CMS, Q be a solid cone and \(\Im :\chi \rightarrow \chi \). Then
-
(1)
ℑ is said to be continuous if \(\lim_{n\rightarrow \infty }p_{n}=p\) implies that \(\lim_{n\rightarrow \infty }fx_{n}=fx\) for all \(\{x_{n}\}\) in X;
-
(2)
ℑ is said to be sequentially convergent if for every sequence \(\{x_{n}\}\) such that \(\{\Im x_{n}\}\) is convergent, \(\{x_{n}\}\) is also convergent.
-
(3)
ℑ is said to be subsequentially convergent if for every sequence \(\{x_{n}\}\) such that \(\{\Im x_{n}\}\) is convergent, \(\{x_{n}\}\) has a convergent subsequence.
2 Main results
We begin this section with a new definition and an example that supports it.
Definition 2.1
Let \((\chi ,\xi )\) be a CbMS with the coefficient \(s\geq 1\), let \(Q\cup (-Q)=B\) (i.e., Q is a total ordering cone), and let \(\Im :\chi \rightarrow \chi \). We will say that a mapping \(\Re :\chi ^{3}\rightarrow \chi \) is a \(\Im _{\theta }\)-contraction if there is \(\theta \in {}[ 0,1)\) such that
for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \).
Example 2.2
Let \(B=\mathbb{R} ^{2}\) and \(Q=\{(p,q)\in B: p,q\geq 0\}\subset B\). Define the distance \(\xi :\chi ^{2}\rightarrow B\) by \(\xi (a,b)= ( \vert a-b \vert ^{i},\gamma \vert a-b \vert ^{i} ) \), where \(\gamma \geq 0\) and \(i>1\) are constants. Define the mappings \(\Im :\chi \rightarrow \chi \) and \(\Re :\chi ^{3}\rightarrow \chi \) by
It is clear that the pair \((B,\xi )\) is a CbMS. If \(p\leq q+r\) for all \(p,q,r\in \chi \), then ℜ is an \(\Im _{\theta }\)-contraction.
On the other hand, take \(p>q+r\), \(q>q^{\ast }\), \(r>r^{\ast }\), and \(\theta =\frac{1}{4^{i}}<1\). Then for all \(p,q,r\in \chi \), we get
Hence the mapping ℜ is an \(\Im _{\theta }\)-contraction, and \((0,0,0)\) is a TFP of ℜ.
The following theorem is the first main result of this paper.
Theorem 2.3
Let the mapping ℜ be an \(\Im _{\theta }\)-contraction (1) defined on CCbMS \((\chi ,\xi )\) with the coefficient \(s\geq 1\) such that B is a solid cone with \(Q\cup (-Q)=B\) and \(\Im :\chi \rightarrow \chi \) is a continuous and one-to-one. Then for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \),
-
(a)
there exist \(\upsilon _{p_{\circ }},\upsilon _{q_{\circ }},\upsilon _{r_{\circ }} \in \chi \) and iterative sequences \(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })=p_{n}\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })=q_{n}\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })=r_{n}\) such that
$$\begin{aligned}& \lim_{n\rightarrow \infty }\Im \Re ^{n}(p_{\circ },q_{\circ },r_{ \circ })= \upsilon _{p_{\circ }}, \qquad \lim_{n\rightarrow \infty } \Im \Re ^{n}(q_{\circ },p_{\circ },q_{\circ })=\upsilon _{q_{\circ }}, \quad \textit{and} \\& \lim_{n\rightarrow \infty }\Im \Re ^{n}(r_{\circ },q_{\circ },p_{ \circ })= \upsilon _{r_{\circ }}; \end{aligned}$$ -
(b)
\(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })\) have a convergent subsequence whenever ℑ is subsequentially convergent;
-
(c)
there are unique \(\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }}\in \chi \) such that \(\Re (\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }})= \sigma _{p_{\circ }}\), \(\Re (\sigma _{q_{\circ }},\sigma _{p_{\circ }},\sigma _{q_{\circ }})= \sigma _{q_{\circ }} \), and \(\Re (\sigma _{r_{\circ }},\sigma _{q_{\circ }},\sigma _{p_{\circ }})= \sigma _{r_{\circ }}\);
-
(d)
for all \(p_{\circ },q_{\circ },r_{\circ }\in \chi \), the sequences \(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })\) converge to \(\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }}\in \chi \), respectively, provided that ℑ is subsequentially convergent.
Proof
For arbitrary \(p_{\circ },q_{\circ },r_{\circ }\in \chi \), we define three sequences as follows:
Applying condition (1), we get
and
Set \(\eta _{n}=\max \{ \xi ( \Im p_{n},\Im p_{n+1} ) , \xi ( \Im q_{n},\Im q_{n+1} ) ,\xi ( \Im r_{n},\Im r_{n+1} ) \} \). By (2)–(4) we have
where \(\theta \in {}[ 0,1)\). Continuing this technique, we can write
If we appoint \(\eta _{\circ }=\vartheta \), then the triple \((p_{\circ },q_{\circ },r_{\circ })\) is a tripled fixed point of ℜ. Assuming that \(\eta _{\circ }>\vartheta \), for all \(m\geq 1\) and \(i\geq 1\), we get
In a similar way, we get
and
Suppose that \(\vartheta \ll \hbar \) is given. Observe that \(\frac{s^{i}\theta ^{m+1}}{s-\theta }\eta _{\circ }+s^{i-1}\theta ^{m}\eta _{ \circ }\rightarrow \vartheta \) as \(m\rightarrow \infty \). By Lemma 1.5 there is \(m_{\circ }\in N\) such that
for each \(m>m_{\circ }\). Hence
for all \(m>m_{\circ }\) and i. Hence Lemma 1.6 implies that \(\{\Im p_{n}\}\), \(\{\Im q_{n}\}\), and \(\{\Im r_{n}\}\) are Cauchy sequences in χ. Since \((\chi ,\xi )\) is complete, there exist \(\upsilon _{p_{\circ }},\upsilon _{q_{\circ }},\upsilon _{r_{\circ }} \in \chi \) such that
Since \(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })\) have convergent subsequences when ℑ is subsequentially convergent, there are \(\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }}\in \chi \) and sequences \(\{p_{n_{w}}\}\), \(\{q_{n_{w}}\}\), and \(\{r_{n_{w}}\}\) such that
Since ℑ is continuous, we have
From another trend, using (10) and (11), we can write
Letting \(w\rightarrow \infty \) in (12) and using (10), we have
which implies that \((1-s)\xi ( \Im \Re (\sigma _{p_{\circ }},\sigma _{q_{\circ }}, \sigma _{r_{\circ }}),\Im \sigma _{p_{\circ }} ) \precsim \vartheta \). Since \(1-s\neq \vartheta \), we have \(\xi ( \Im \Re (\sigma _{p_{\circ }}, \sigma _{q_{\circ }}, \sigma _{r_{\circ }}),\Im \sigma _{p_{\circ }} ) =\vartheta \), that is, \(\Im \Re (\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{ \circ }})=\Im \sigma _{p_{\circ }}\). Similarly, we obtain \(\Im \Re (\sigma _{q_{\circ }},\sigma _{p_{\circ }},\sigma _{q_{ \circ }})=\Im \sigma _{q_{\circ }}\) and \(\Im \Re (\sigma _{r_{\circ }},\sigma _{q_{\circ }},\sigma _{p_{ \circ }})=\Im \sigma _{r_{\circ }}\). Since ℑ is one-to-one, we have \(\Re (\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }})= \sigma _{p_{\circ }}\), \(\Re (\sigma _{q_{\circ }},\sigma _{p_{\circ }},\sigma _{q_{\circ }})= \sigma _{q_{\circ }}\), and \(\Re (\sigma _{r_{\circ }},\sigma _{q_{\circ }},\sigma _{p_{\circ }})= \sigma _{r_{\circ }}\). Therefore there is a tripled fixed point \((\sigma _{p_{\circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }})\) of ℜ.
Let us assume that there is another TFP of ℜ of the form \((\eth _{p_{\circ }},\eth _{q_{\circ }},\eth _{r_{\circ }})\). Then
and
By Lemma 1.7 we get
Hence \(\Im \sigma _{p_{\circ }}=\Im \eth _{p_{\circ }}\), \(\Im \sigma _{q_{\circ }}=\Im \eth _{q_{\circ }}\), and \(\Im \sigma _{r_{\circ }}=\Im \eth _{r_{\circ }}\). Since ℑ is one-to-one, we can write \((\eth _{p_{\circ }},\eth _{q_{\circ }},\eth _{r_{\circ }})=(\sigma _{p_{ \circ }},\sigma _{q_{\circ }},\sigma _{r_{\circ }})\). Finally, if ℑ is subsequentially convergent, then substituting \(n_{w}\) with n into (9), we can get
This ends the proof. □
Example 2.4
Let \(\chi =[0,1]\), \(B=\mathbb{R} ^{2}\), and \(i>1\). Specify \(Q=\{(p,q)\in B: p,q\geq 0\}\). Realize the function \(\xi :\chi ^{2}\rightarrow B\) as
Assuming that \(\Im :\chi \rightarrow \chi \) and \(\Re :\chi ^{3}\rightarrow \chi \) are defined as
It is obvious that \((B,\xi )\) is a CCbMS and ℑ is continuous and one-to-one. To fulfill (11), we take \(\theta =\frac{1}{8^{i}}\), \(i>1\). Then for all \(p,q,r\in \chi \), we have
Therefore ℜ is an \(\Im _{\theta }\)-contraction. Now we verify the remaining conditions as follows:
-
(a)
let \((\frac{1}{6},\frac{1}{6},\frac{1}{6})\in \chi \), and consider the iterative sequences \(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })=\{\frac{1}{n}\}_{n\in N}=p_{n}\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })=\{\frac{n^{2}}{n+7}\}_{n\in N}=q_{n}\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })=\{\frac{1}{e^{n}}\}_{n\in N}=r_{n}\). Then
$$\begin{aligned}& \lim_{n\rightarrow \infty }\Im \Re ^{n}(p_{\circ },q_{\circ },r_{ \circ }) = \Im \Bigl( \lim_{n\rightarrow \infty }\Re ^{n}(p_{ \circ },q_{\circ },r_{\circ }) \Bigr) =\Im \biggl( \lim_{n \rightarrow \infty }\frac{1}{n} \biggr) =\Im ( 0 ) =\frac{1}{6},\text{ } \\& \lim_{n\rightarrow \infty }\Im \Re ^{n}(q_{\circ },p_{\circ },q_{ \circ }) = \Im \biggl( \lim_{n\rightarrow \infty }\frac{n^{2}}{n+7} \biggr) =\Im ( 0 ) =\frac{1}{6}, \\& \lim_{n\rightarrow \infty }\Im \Re ^{n}(r_{\circ },q_{\circ },p_{ \circ }) = \Im \biggl( \lim_{n\rightarrow \infty }\frac{1}{e^{n}} \biggr) =\Im ( 0 ) =\frac{1}{6}; \end{aligned}$$ -
(b)
intuitively achieved;
-
(c)
there is a unique point \((0,0,0)\in \chi \), as required;
-
(d)
if ℑ is subsequentially convergent, then the sequences \(\Re ^{n}(p_{\circ },q_{\circ },r_{\circ })\), \(\Re ^{n}(q_{\circ },p_{\circ },q_{\circ })\), and \(\Re ^{n}(r_{\circ },q_{\circ },p_{\circ })\) converge to \((0,0,0)\in \chi \).
Hence all the conditions of Theorem 2.3 are fulfilled, and \((0,0,0)\) is a unique TFP of the mapping ℜ.
Theorem 2.5
Suppose that \((\chi ,\xi )\) is a CCbMS with coefficient \(s\geq 1\), B is a solid cone with \(Q\cup (-Q)=B\), \(\Im :\chi \rightarrow \chi \) is a continuous one-to-one mapping, and \(\Re :\chi ^{3}\rightarrow \chi \) is a mapping such that
for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \), where \(\theta \in {}[ 0,1)\). Then the conclusion of Theorem 2.3is achieved.
Proof
The proof immediately follows from Theorem 2.3. □
Theorem 2.6
Suppose that \((\chi ,\xi )\) is a CCbMS with coefficient \(s\geq 1\), B is a solid cone with \(Q\cup (-Q)=B\), \(\Im :\chi \rightarrow \chi \) is a continuous one-to-one mapping, and \(\Re :\chi ^{3}\rightarrow \chi \) is a mapping such that
for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \), where \(\theta \in {}[ 0,1)\). Then the conclusion of Theorem 2.3is achieved.
Proof
The proof immediately follows from Theorem 2.3. □
The following corollary contains some contractive terms inspired by Theorem 2.3.
Corollary 2.7
Suppose that \((\chi ,\xi )\) is a CCbMS with coefficient \(s\geq 1\), B is a solid cone with \(Q\cup (-Q)=B\), \(\Im :\chi \rightarrow \chi \) is a continuous one-to-one mapping, and \(\Re :\chi ^{3}\rightarrow \chi \) is a mapping such that one of the following conditions holds:
- \((\spadesuit _{1})\):
-
$$ \xi \bigl( \Im \Re (p,q,r),\Im \Re \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr) \bigr) \precsim \theta \xi \bigl( \Im p,\Im p^{\ast } \bigr), $$
- \((\spadesuit _{2})\):
-
$$\begin{aligned}& \xi \bigl( \Im \Re (p,q,r),\Im \Re \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr) \bigr) \\& \quad \precsim \theta \max \left\{ \begin{aligned} &\xi \bigl( \Im p,\Im p^{\ast } \bigr) ,\xi \bigl( \Im q,\Im q^{ \ast } \bigr) ,\xi \bigl( \Im r,\Im r^{\ast } \bigr) , \\ &\frac{\xi ( \Im p,\Im p^{\ast } ) +\xi ( \Im q,\Im q^{\ast } ) +\xi ( \Im r,\Im r^{\ast } ) }{3}\end{aligned} \right\} , \end{aligned}$$
- \((\spadesuit _{3})\):
-
$$\begin{aligned}& \xi \bigl( \Im \Re (p,q,r),\Im \Re \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr) \bigr) \\& \quad \precsim \theta \max \left\{ \begin{aligned} &\xi \bigl( \Im \Re (p,q,r),\Im p \bigr) ,\xi \bigl( \Im \Re \bigl(p^{ \ast },q^{\ast },r^{\ast } \bigr),\Im p \bigr) , \\ & \frac{\xi ( \Im \Re (p,q,r),\Im p^{\ast } ) +\xi ( \Im \Re (p^{\ast },q^{\ast },r^{\ast }),\Im p ) }{2}\end{aligned} \right\} , \end{aligned}$$
- \((\spadesuit _{4})\):
-
$$\begin{aligned}& \xi \bigl( \Im \Re (p,q,r),\Im \Re \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr) \bigr) \\& \quad \precsim \theta \max \left\{ \begin{aligned} &\xi \bigl( \Im \Re (p,q,r),\Im p^{\ast } \bigr) ,\xi \bigl( \Im \Re \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr),\Im p \bigr) , \\ & \frac{\xi ( \Im \Re (p,q,r),\Im p^{\ast } ) +\xi ( \Im \Re (p^{\ast },q^{\ast },r^{\ast }),\Im p ) }{2}\end{aligned} \right\} \end{aligned}$$
for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \), where \(\theta \in {}[ 0,1)\). Then the conclusion of Theorem 2.3is achieved.
Now we can discuss another generalization of our results.
Lemma 2.8
Let \((\chi ,\xi )\) be a CCbMS with coefficient \(s\geq 1\). Then we have the following two properties:
- \((\heartsuit _{1})\):
-
\((\chi \times \chi \times \chi ,\xi _{1})\) is a CCbMS equipped with
$$ \xi _{1} \bigl((p,q,r), \bigl(p^{\ast },q^{\ast },r^{\ast } \bigr) \bigr)=\max \bigl\{ \xi \bigl(p,p^{ \ast } \bigr),\xi \bigl(q,q^{\ast } \bigr),\xi \bigl(r,r^{\ast } \bigr) \bigr\} ; $$ - \((\heartsuit _{2})\):
-
If the mapping \(\Gamma _{\Re }:\chi ^{3}\rightarrow \chi ^{3}\) defined by the relation \(\Gamma _{\Re }(p,q,r)= ( \Re (p,q,r), \Re (q,p,q),\Re (r,q,p) ) \) has a fixed point in \(\chi ^{3}\), then the mapping \(\Re :\chi ^{3}\rightarrow \chi \) has a tripled fixed point, and the opposite is generally true.
Proof
\((\heartsuit _{1})\) Hypotheses \((cb_{1})\) and \((cb_{1})\) of Definition 1.3 are fulfilled. Just check the triangle inequality. Since \((\chi ,\xi )\) is a CbMS, we have
for all \((p,q,r),(p^{\ast },q^{\ast },r^{\ast }),(\wp ,\partial ,\hbar )\in \chi ^{3}\). Again, the completeness of \((\chi ,\xi )\) leads to the completeness of \((\chi ^{3},\xi _{1})\). Therefore \((\chi ^{3},\xi _{1})\) is a CCbMS.
\((\heartsuit _{2})\) Let there is a tripled fixed point \((p,q,r)\) of ℜ, that is, \(\Re (p,q,r)=p\), \(\Re (q,p,q)=q\), and \(\Re (r,q,p)=r\). Hence
that is, a triple \((p,q,r)\) is a fixed point of \(\Gamma _{\Re }\). Vice versa, Let \((p,q,r)\in \chi ^{3}\) be a fixed point of the mapping \(\Gamma _{\Re }\). Then \(\Gamma _{\Re }(p,q,r)=(p,q,r)\), which yields, \(\Re (p,q,r)=p \), \(\Re (q,p,q)=q\), and \(\Re (r,q,p)=r\). □
Theorem 2.9
Assume that \((\chi ,\xi )\) is a CCbMS with coefficient \(s\geq 1\), B is a total ordering solid cone, \(\Im :\chi \rightarrow \chi \) is a continuous one-to-one mapping, and \(\Re :\chi ^{3}\rightarrow \chi \) is a mapping such that the following hypothesis are satisfied:
for all \(p,q,r,p^{\ast },q^{\ast },r^{\ast }\in \chi \), where \(\theta \in {}[ 0,1)\). Then the conclusion of Theorem 2.3is achieved.
Proof
We begin by defining the mapping  as
as  . Note that
. Note that  is one-to-one and continuous. Allocate \(\aleph =(p,q,r)\) and \(\gimel =(p^{\ast },q^{\ast },r^{\ast })\in \chi ^{3}\) and apply the hypotheses of Lemma 2.8. Then condition (16) reduces to
is one-to-one and continuous. Allocate \(\aleph =(p,q,r)\) and \(\gimel =(p^{\ast },q^{\ast },r^{\ast })\in \chi ^{3}\) and apply the hypotheses of Lemma 2.8. Then condition (16) reduces to

So, the proof is finished by condition \((\spadesuit _{1})\) of Corollary 2.7. □
Example 2.10
Let \(\chi =[0,1]\), and let \(B=C_{\mathbb{R} }^{1}[0,1]\) be a family of real-valued functions on χ with continuous derivatives on χ. Define the distance \(\xi (p,q)= \vert p-q \vert ^{i}e^{\kappa }\), where \(i\geq 1\) is a constant, and \(e^{\kappa }\in B\) on \(Q= \{ \psi \in B:\psi \geq 0 \} \). Hence \((\chi ,\xi )\) is a CCbMS with coefficient \(s=2^{i}\). Define two mappings \(\Im :\chi \rightarrow \chi \) and \(\Re :\chi ^{3}\rightarrow \chi \) by
It is easy to write
Similarly, we have
Therefore relations (17)–(19) demonstrate verification of stipulation (16) for all \(p,q,r, p^{\ast },q^{\ast },r^{\ast }\in \chi \) and \(\theta =\frac{3}{7^{i}}\). As in Example 2.4, we find that the remaining conditions of Theorem 2.3 are fulfilled. Thus a triple \((0,0,0)\) is a unique tripled fixed point of ℜ.
3 Solve a tripled system of integral equations
In this part, we use the theoretical results obtained in the previous section to clarify the existence and uniqueness of the solution for the following system:

for all \(\gimel \in {}[ 0,\wp ]\). Postulate the following assumptions:
- \(\blacktriangledown _{1}\):
-
\(\aleph :[0,\wp ]\rightarrow \mathbb{R} \) and
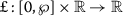 are continuous;
are continuous; - \(\blacktriangledown _{2}\):
-
\(\Game _{l}:[0,\wp ]\times \mathbb{R} \rightarrow \mathbb{R} \) (\(l=1,2,3\)) are continuous;
- \(\blacktriangledown _{3}\):
-
there is a constant \(\amalg >0\) such that for all \(p,q\in \mathbb{R} \),
$$\begin{aligned}& 0 \precsim \Game _{1}(\mho ,p)-\Game _{1}(\mho ,q) \precsim \amalg (p-q), \\& 0 \precsim \Game _{2}(\mho ,p)-\Game _{2}(\mho ,q) \precsim \amalg (p-q), \\& 0 \precsim \Game _{3}(\mho ,p)-\Game _{3}(\mho ,q) \precsim \amalg (p-q); \end{aligned}$$ - \(\blacktriangledown _{4}\):
-
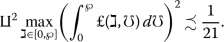
Let \(\chi =C([0,\wp ],\mathbb{R} )\) be the set of all continuous real-valued functions on \([0,\wp ]\) taking values in \(\mathbb{R}\), and let \(Q=\{\pi \in B:\pi \geq 0\}\). Set \(\xi :\chi \times \chi \rightarrow B\) as \(\xi (o,O)=e^{\gimel }\max_{\gimel \in {}[ 0,\wp ]} \vert o( \gimel )-O(\gimel ) \vert ^{2}\). It is obvious that \((\chi ,\xi )\) is a CCbMS.
Our main theorem is the following:
Theorem 3.1
Under hypotheses \((\blacktriangledown _{1})\)–\((\blacktriangledown _{4})\), problem (20) has a solution in \(\chi ^{3}\), where \(\chi =C([0,\wp ],\mathbb{R} )\).
Proof
Define the operators \(\Re :\chi ^{3}\rightarrow \chi \) and \(\Im :\chi \rightarrow \chi \) by

and \(\Im (\zeta )=\zeta \) for all \(\gimel \in {}[ 0,\wp ]\) and \(\zeta _{1},\zeta _{2},\zeta _{3}\in \chi \). The triple \((\zeta _{1},\zeta _{2},\zeta _{3})\) is a solution of system (20) if and only if \((\zeta _{1},\zeta _{2},\zeta _{3})\) is a tripled fixed point of ℜ. The existence of this triple follows from Theorem 2.3, since ℑ is the identity mapping. Therefore it is necessary to fulfill the remaining conditions of Theorem 2.3. For all \(\zeta _{1},\zeta _{2},\zeta _{3}\in \chi \) and \(\gimel \in {}[ 0,\wp ]\), setting \(\theta =\frac{3}{7}\), we get

This means that condition (1) of Theorem 2.3 is fulfilled. Thus ℜ has a tripled fixed point \((\zeta _{1},\zeta _{2},\zeta _{3})\in C([0,\wp ],\mathbb{R} )\times C([0,\wp ],\mathbb{R} )\times C([0,\wp ],\mathbb{R} )\), which, at the same time, is a solution to problem (20). □
4 A stationary distribution of the Markov process
Suppose that \(\mathbb{R} _{+}^{n}=\{(\delta _{1},\delta _{2},\ldots,\delta _{n})= \delta :\delta _{\ell }\geq 0, \ell \geq 1\}\) and \(\Omega _{n-1}^{3}=\{\sigma =(p,q,r)\in \mathbb{R} _{+}^{n}\times \mathbb{R} _{+}^{n}\times \mathbb{R} _{+}^{n}:\sum_{\ell =1}^{n}\sigma _{\ell }=\sum_{\ell =1}^{n} ( p_{\ell }+q_{\ell }+r_{\ell } ) =1 \}\) refer to the \(3(n-1)\)-dimensional unit simplex and \(\sigma \in \Omega _{n-1}^{3}\) is considered as a possibility over 3n possible statuses. Here the Markov process is a stochastic process such that 3n statuses are realized in each period \(\gimel =1,2,\ldots \) with probability contingent on the current achieved status. Assume that \(a_{\ell \kappa }\) refer to the probability contingent that status ℓ is achieved in the subsequent period beginning in status κ. Hence in periods ℷ and \(\gimel +1\) the prior probability vector \(\sigma ^{\gimel }\) and the posterior probability \(\sigma ^{\gimel +1}\) are given by \(\sigma _{\ell }^{\gimel +1}=\sum_{\ell }a_{\ell \kappa } \sigma _{\kappa }^{\gimel }\) for each \(\ell \geq 1\). To write this in matrix form, we consider \(\sigma ^{\gimel }\) as a column vector, and then \(\sigma ^{\gimel +1}=\Theta \sigma ^{\gimel }\). Note that \(a_{\ell \kappa }\geq 0\) and \(\sum_{\ell =1}^{n}a_{\ell \kappa }=1\), which is required for conditional probability. The vector \(\sigma ^{\gimel }\) is called a stationary distribution of the Markov process at any period if \(\sigma ^{\gimel }=\sigma ^{\gimel +1}\). This mean that the problem of finding a stationary distribution is equivalent to the fixed point problem \(\Theta \sigma ^{\gimel }=\sigma ^{\gimel }\).
Suppose that \(\delta _{\ell }=\min_{\kappa }a_{\ell \kappa }\) and define \(\delta =\sum_{\ell =1}^{n}\delta _{\ell }\).
Before presenting our main theorem of this section, we need the following inequality.
Minkowski’s Inequality
(Theorem 6, [42], p. 25)
For \(p_{i},q_{i}\geq 0\) and \(\alpha >1\), we have
Theorem 4.1
There exists a unique stationary distribution for the Markov process whenever \(a_{\ell \kappa }\geq 0\).
Proof
Let \(\xi :\Omega _{n-1}^{3}\times \Omega _{n-1}^{3}\rightarrow \mathbb{R} ^{2}\) be defined by
for all \(\Phi ,\Psi \in \Omega _{n-1}^{3}\), with \(\alpha \geq 1\).
It is obvious that \(\xi ( \Phi ,\Psi ) \geq (0,0)\) for all \(\Phi ,\Psi \in \Omega _{n-1}^{3}\), and if \(\xi ( \Phi ,\Psi ) =(0,0)\), then this leads to \(( \{ \sum_{\ell =1}^{n} ( \vert p_{ \ell }-p_{\ell }^{\ast } \vert + \vert q_{\ell }-q_{\ell }^{ \ast } \vert + \vert r_{\ell }-r_{\ell }^{\ast } \vert ) ^{\alpha } \} ^{\frac{1}{\alpha }}, \{ \sum_{\ell =1}^{n} ( \vert p_{\ell }-p_{\ell }^{ \ast } \vert + \vert q_{\ell }-q_{\ell }^{\ast } \vert + \vert r_{\ell }-r_{\ell }^{\ast } \vert ) ^{ \alpha } \} ^{\frac{1}{\alpha }} ) =(0,0)\), and thus \(\vert p_{\ell }-p_{\ell }^{\ast } \vert + \vert q_{ \ell }-q_{\ell }^{\ast } \vert + \vert r_{\ell }-r_{\ell }^{ \ast } \vert =0\) for all ℓ, which leads to \(p=p^{\ast }\), \(q=q^{\ast }\), and \(r=r^{\ast }\), that is, \(\Phi =\Psi \). On the other hand, if \(\Phi =\Psi \), then \(p_{\ell }=p_{\ell }^{\ast }\), \(q_{\ell }=q_{\ell }^{\ast }\), and \(r_{\ell }=r_{\ell }^{\ast }\) for all ℓ, and thus \(\vert p_{\ell }-p_{\ell }^{\ast } \vert = \vert q_{ \ell }-q_{\ell }^{\ast } \vert = \vert r_{\ell }-r_{\ell }^{ \ast } \vert =0\), which yields \(( \{ \sum_{\ell =1}^{n} ( \vert p_{ \ell }-p_{\ell }^{\ast } \vert + \vert q_{\ell }-q_{\ell }^{ \ast } \vert + \vert r_{\ell }-r_{\ell }^{\ast } \vert ) ^{\alpha } \} ^{\frac{1}{\alpha }}, \{ \sum_{\ell =1}^{n} ( \vert p_{\ell }-p_{\ell }^{ \ast } \vert + \vert q_{\ell }-q_{\ell }^{\ast } \vert + \vert r_{\ell }-r_{\ell }^{\ast } \vert ) ^{ \alpha } \} ^{\frac{1}{\alpha }} ) =0\Rightarrow \xi ( \Phi ,\Psi ) =0\).
We also have
Now we can write
for \(\Xi = ( \tau ,\eta ,\omega ) \in \Omega _{n-1}^{3}\). Thus \((\Omega _{n-1}^{3},\xi )\) is a CbMS with \(s=2^{\alpha }\) and \(Q=\{(\delta _{1},\delta _{2},\ldots,\delta _{n}):\delta _{\ell }\geq 0, \ell \geq 1\}\).
Let \(\Psi =\Theta \sigma \) for all \(\Psi \in \Omega _{n-1}^{3}\). Therefore each \(\rho _{\ell }=\sum_{\kappa =1}^{n}a_{\ell \kappa }\sigma _{ \kappa }\geq 0\). Moreover, since each \(\sum_{\kappa =1}^{n}a_{\ell \kappa }=1\), we get
which shows that \(\Psi \in \Omega _{n-1}^{3}\). Thus we can write \(\Theta :\Omega _{n-1}^{3}\rightarrow \Omega _{n-1}^{3}\). Now we will prove that Θ is a contraction.
Let \(\Theta _{\ell }\) refer to the ℓth row of Θ. So for any \(( p,q,r ) ,(p^{\ast },q^{\ast },r^{\ast })\in \Omega _{n-1}^{3}\) and all \(\alpha \geq 1\), we get (note that \(\sum_{\kappa =1}^{n} ( p_{\kappa }+q_{\kappa }+r_{ \kappa } ) =1\))
which proves that Θ is a contraction. Hence if the mapping \(\Im =I_{\chi }\) is the identity mapping in Theorem 2.3, then the Markov process has a unique stationary distribution, and the sequence \(\{ \Theta ^{n}\sigma ^{\dagger } \} \) converges to this distribution for any \(\sigma ^{\dagger }\in \Omega _{n-1}^{3}\). □
References
Fredholm, E.I.: Sur une classe d’équations fonctionnelles. Acta Math. 27, 365–390 (1903)
Rus, M.D.: A note on the existence of positive solution of Fredholm integral equations. Fixed Point Theory 5, 369–377 (2004)
Berenguer, M.I., Munoz, M.V.F., Guillem, A.I.G., Galan, M.R.: Numerical treatment of fixed point applied to the nonlinear Fredholm integral equation. Fixed Point Theory Appl. 2009, Article ID 735638 (2009)
Hammad, H.A., De la Sen, M.: A solution of Fredholm integral equation by using the cyclic \(\eta _{s}^{q}\)-rational contractive mappings technique in b-metric-like spaces. Symmetry 11, 1184 (2019)
Hammad, H.A., De la Sen, M.: Solution of nonlinear integral equation via fixed point of cyclic \(\alpha _{s}^{q}\)-rational contraction mappings in metric-like spaces. Bull. Braz. Math. Soc. 51, 81–105 (2020)
Bhaskar, T.G., Lakshmikantham, V.: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. TMA 65, 1379–1393 (2006)
Abbas, M., Khan, M.A., Radenović, S.: Common coupled fixed point theorems in cone metric spaces for w-compatible mappings. Appl. Math. Comput. 217, 195–202 (2010)
Aydi, H., Postolache, M., Shatanawi, W.: Coupled fixed point results for \((\psi ,\phi )\)-weakly contractive mappings in ordered G-metric spaces. Comput. Math. Appl. 63, 298–309 (2012)
Berinde, V.: Coupled fixed point theorems for contractive mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 75, 3218–3228 (2012)
Choudhury, B.S., Maity, P.: Coupled fixed point results in generalized metric spaces. Math. Comput. Model. 54, 73–79 (2011)
Cirić, L., Damjanović, B., Jleli, M., Samet, B.: Coupled fixed point theorems for generalized Mizoguchi–Takahashi contraction and applications to ordinary differential equations. Fixed Point Theory Appl. 2012, Article ID 51 (2012)
Ding, H.S., Li, L., Radenovic, S.: Coupled coincidence point theorems for generalized nonlinear contraction in partially ordered metric spaces. Fixed Point Theory Appl. 2012, Article ID 96 (2012)
Hammad, H.A., De la Sen, M.: A coupled fixed point technique for solving coupled systems of functional and nonlinear integral equations. Mathematics 7, 634 (2019)
Luong, N.V., Thuan, N.X.: Coupled fixed points in partially ordered metric spaces and application. Nonlinear Anal. 74, 983–992 (2011)
Razani, A., Parvaneh, V.: Coupled coincidence point results for \((\psi ,\alpha ,\beta )\)-weak contractions in partially ordered metric spaces. J. Appl. Math. 2012, Article ID 496103 (2012)
Shatanawi, W.: Coupled fixed point theorems in generalized metric spaces. Hacet. J. Math. Stat. 40, 441–447 (2011)
Sintunavarat, W., Cho, Y.J., Kumam, P.: Coupled coincidence point theorems for contractions without commutative condition in intuitionistic fuzzy normed spaces. Fixed Point Theory Appl. 2011, Article ID 81 (2011)
Sintunavarat, W., Cho, Y.J., Kumam, P.: Coupled fixed point theorems for weak contraction mapping under F-invariant set. Abstr. Appl. Anal. 2012, Article ID 324874 (2012)
Karapınar, E., Kumam, P., Sintunavarat, W.: Coupled fixed point theorems in cone metric spaces with a c-distance and applications. Fixed Point Theory Appl. 2012, Article ID 194 (2012)
Agarwal, R.P., Sintunavarat, W., Kumam, P.: Coupled coincidence point and common coupled fixed point theorems lacking the mixed monotone property. Fixed Point Theory Appl. 2013, Article ID 22 (2013)
Hammad, H.A., Albaqeri, D.M., Rashwan, R.A.: Coupled coincidence point technique and its application for solving nonlinear integral equations in RPOCbML spaces. J. Egypt. Math. Soc. 28, Article ID 8 (2020). https://doi.org/10.1186/s42787-019-0064-3
Berinde, V., Borcut, M.: Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces. Nonlinear Anal. 74, 4889–4897 (2011)
Borcut, M.: Tripled coincidence theorems for contractive type mappings in partially ordered metric spaces. Appl. Math. Comput. 218, 7339–7346 (2012)
Borcut, M., Berinde, V.: Tripled coincidence theorems for contractive type mappings in partially ordered metric spaces. Appl. Math. Comput. 218, 5929–5936 (2012)
Choudhury, B.S., Karapınar, E., Kundu, A.: Tripled coincidence point theorems for nonlinear contractions in partially ordered metric spaces. Int. J. Math. Math. Sci. 2012, Article ID 329298 (2012)
Aydi, H., Abbas, M., Sintunavarat, W., Kumam, P.: Tripled fixed point of W-compatible mappings in abstract metric spaces. Fixed Point Theory Appl. 2012, Article ID 134 (2012)
Mustafa, Z., Roshan, J.R., Parvaneh, V.: Existence of a tripled coincidence point in ordered \(G_{b}\)-metric spaces and applications to a system of integral equations. J. Inequal. Appl. 2013, 453 (2013)
Aydi, H., Karapinar, E., Postolache, M.: Tripled coincidence point theorems for weak φ-contractions in partially ordered metric spaces. Fixed Point Theory Appl. 2012, 44 (2012)
Hammad, H.A., De la Sen, M.: A technique of tripled coincidence points for solving a system of nonlinear integral equations in POCML spaces. J. Inequal. Appl. 2020, 211 (2020). https://doi.org/10.1186/s13660-020-02477-8
Shatanawi, W., Postolache, M., Mustafa, Z.: Tripled and coincidence fixed point theorems for contractive mappings satisfying Φ-maps in partially ordered metric spaces. An. Ştiinţ. Univ. ‘Ovidius’ Constanţa 22(3), 179–203 (2014)
Bakhtin, I.A.: The contraction mapping principle in almost metric spaces. Funct. Anal. Gos. Ped. Inst. Ulyanovsk. 30, 26–37 (1989)
Czerwik, S.: Nonlinear set-valued contraction mappings in b-metric spaces. Atti Semin. Mat. Fis. Univ. Modena 46, 263–276 (1998)
Boriceanu, M., Bota, M., Petrusel, A.: Multivalued fractals in b-metric spaces. Cent. Eur. J. Math. 8(2), 367–377 (2010)
Bota, M., Molnar, A., Csaba, V.: On Ekeland’s variational principle in b-metric spaces. Fixed Point Theory 12, 21–28 (2011)
Huang, L.G., Zhang, X.: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 332(2), 1468–1476 (2007)
Hussian, N., Shah, M.H.: KKM mappings in cone b-metric spaces. Comput. Math. Appl. 62, 1677–1684 (2011)
Huang, H., Xu, S.: Fixed point theorems of contractive mappings in cone b-metric spaces and applications. Fixed Point Theory Appl. 2013, 112 (2013)
Janković, S., Kadelburg, Z., Radenović, S.: On cone metric spaces: a survey. Nonlinear Anal. 4(7), 2591–2601 (2011)
Cho, S.H., Bae, J.S.: Common fixed point theorems for mappings satisfying property (E.A) on cone metric space. Math. Comput. Model. 53, 945–951 (2011)
Berinde, V., Borcut, M.: Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces. Nonlinear Anal. 74, 4889–4897 (2011)
Filipovic, M., Paunović, L., Radenović, S., Rajović, M.: Remarks on cone metric spaces and fixed point theorems of T-Kannan and T-Chatterjea contractive mappings. Math. Comput. Model. 54, 1467–1472 (2011)
Beckenbach, E.F., Bellman, R.: Inequalities. Springer, Berlin (1961)
Acknowledgements
The authors are thankful to the editor for his valuable comments and suggestions.
Availability of data and materials
The data used to support the findings of this study are available from the corresponding author upon request.
Funding
This work was supported in part by the Basque Government under Grant IT1207-19. The authors are also grateful to Spanish Government and the European Commission by Grant RTI2018-094336-BI00 (MCIU/AEI/FEDER, UE).
Author information
Authors and Affiliations
Contributions
Both authors contributed equally and significantly in writing this paper. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hammad, H.A., De La Sen, M. A tripled fixed point technique for solving a tripled-system of integral equations and Markov process in CCbMS. Adv Differ Equ 2020, 567 (2020). https://doi.org/10.1186/s13662-020-03023-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03023-y
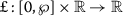 are continuous;
are continuous;