- Research
- Open access
- Published:
Proinov type contractions on dislocated b-metric spaces
Advances in Difference Equations volume 2021, Article number: 164 (2021)
Abstract
In this paper, we improve the Proinov theorem by adding certain rational expressions to the definition of the corresponding contractions. After that, we prove fixed point theorems for these modified Proinov contractions in the framework of dislocated b-metric spaces. We show some illustrative examples to indicate the validity of the main results.
1 Introduction and preliminaries
In the nature of mathematics, there is the purpose of generalizing, expanding, and obtaining the most general forms of existing concepts and results. The concept of metric, which is the most fundamental and solid basis of the analysis study, has been constantly expanded and generalized with this motivation. Examples of the new metrics that have been put forward for this purpose can be counted as quasi-metric, b-metric, partial-metric, symmetric, D-metric, modular metric, fuzzy metric, soft-metric, G-metric, and so on. On the other hand, it was understood that not all of these newly defined metrics provide a new and original structure. For instance, G-metric can be reduced to semi-metric or cone metric to a standard metric. More examples can be given, but here we stop to focus on the main motivation. Two of the new and original generalizations of metric notions are b-metrics [1–16] and dislocated metrics [17–21]. Very recently, these two notions have emerged under the name of dislocated b-metric [22, 23].
Metric fixed point theory is a field of study that needs an abstract metric framework (see, for instance, [24–27]). Very recently Proinov [28] proved a fixed point theorem that not only unifies but also generalizes a number of well-known results in the framework of a standard metric space. In particular, he proved that Wardowski [29] and Jleli and Samet [30] results are not only equivalent to each other, but also they are a special case of one of the main results of [28].
In this paper, we improve the Proinov type contractions by involving certain rational expression to the corresponding contraction thought by Proinov [28]. After then, we prove fixed point theorems for these modified Proinov contractions in the framework of dislocated b-metrics. We bring forward illustrative examples to show the validity of the main results.
Let S be a nonempty set and \(\mathbb{N}=\{1,2,3,\ldots \}\). Some examples of rational contractivity conditions are shown in the following results (see also [31]).
Theorem 1
([32])
Let  be a complete metric space and
be a complete metric space and  be a mapping such that there exist
be a mapping such that there exist  with
with  such that
such that

for all \(\mathsf {v},\mathsf {w}\in \mathsf {S}\). Then  has a unique fixed point \(\mathsf {x}\in \mathsf {S}\), and the sequence
has a unique fixed point \(\mathsf {x}\in \mathsf {S}\), and the sequence  converges to the fixed point x for all \(\mathsf {v}\in \mathsf {S}\).
converges to the fixed point x for all \(\mathsf {v}\in \mathsf {S}\).
Theorem 2
([33])
Let  be a complete metric space and
be a complete metric space and  be a continuous mapping. If there exist
be a continuous mapping. If there exist  with
with  such that
such that

for all distinct \(\mathsf {v},\mathsf {w}\in \mathsf {S}\), then  possesses a unique fixed point in S.
possesses a unique fixed point in S.
Theorem 3
([28])
Let  be a metric space and
be a metric space and  be a mapping such that
be a mapping such that

for all \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , where the functions \(\Psi, \Phi:(0,\infty )\rightarrow \mathbb{R}\) are such that the following conditions are satisfied:
, where the functions \(\Psi, \Phi:(0,\infty )\rightarrow \mathbb{R}\) are such that the following conditions are satisfied:
-
1.
Ψ is nondecreasing;
-
2.
\(\Phi (\theta )<\Psi (\theta )\) for any \(\theta >0\);
-
3.
\(\limsup_{\theta \rightarrow \theta _{0}+}\Phi ( \theta )<\Psi (\theta _{0}+)\) for any \(\theta _{0}>0\).
Then  admits a unique fixed point.
admits a unique fixed point.
Definition 4
([34])
A function \(\mathsf{d}_{l}:\mathsf {S}\times \mathsf{S}\rightarrow [ 0,\infty )\) is a dislocated-metric on S if it satisfies the conditions:
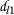 .:
.:-
\(\mathsf{d}_{l}(\mathsf {v},\mathsf {w})=0 \Rightarrow \mathsf {v}= \mathsf {w}\);
 .:
.:-
symmetry: \(\mathsf{d}_{l} (\mathsf {w},\mathsf {v})=\mathsf{d}_{l}(\mathsf {v},\mathsf {w})\);
 .:
.:-
the triangle inequality
$$\begin{aligned} \mathsf{d}_{l}(\mathsf{u},\mathsf{w} )\leq \mathsf{d}_{l} ( \mathsf{u}, \mathsf{v})+\mathsf{d}_{l}(\mathsf{v},\mathsf{w} ) \end{aligned}$$
for all \(\mathsf{u},\mathsf{v},\mathsf{w} \in \mathsf {S}\). In this case, the pair  is a dislocated-metric space (shortly
is a dislocated-metric space (shortly  -MS).
-MS).
Definition 5
([35])
Let \(\mathsf{s}\in [1,\infty )\) be a real number. A function \(\mathsf{b}:\mathsf {S}\times \mathsf{S}\rightarrow [ 0,\infty )\) is a b-metric on S if it satisfies the conditions:
- \(\mathsf {b}_{1}\).:
-
\(\mathsf{b}(\mathsf {v},\mathsf {w})=0 \Leftrightarrow \mathsf {v}=\mathsf {w}\),
- \(\mathsf {b}_{2}\).:
-
symmetry: \(\mathsf{b}(\mathsf {w},\mathsf {v})=\mathsf{b}(\mathsf {v},\mathsf {w})\)
- \(\mathsf {b}_{3}\).:
-
the generalized version of the triangle inequality involving the number s
$$\begin{aligned} \mathsf{b}(\mathsf{u},\mathsf{w} )\leq \mathsf{s } \bigl[ \mathsf{ b}( \mathsf{u},\mathsf{v})+\mathsf{b}(\mathsf{v},\mathsf{w} )\mathsf{ } \bigr] \quad\text{for all }\mathsf{u},\mathsf{v},\mathsf{w} \in \mathsf {S}. \end{aligned}$$
In this case, the tripled \((\mathsf {S}, \mathsf {b}, \mathsf {s})\) forms a b-metric space (shortly b-MS).
Obviously, for \(\mathsf{s}=1\), we find the notion of metric space.
Definition 6
([36])
Let \(\mathsf{s}\in [1,\infty )\) be a real number(given). A function  is a dislocated b-metric on S if it satisfies the conditions:
is a dislocated b-metric on S if it satisfies the conditions:
 .:
.:-
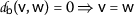 ;
;  .:
.:-
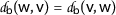 ;
;  .:
.:-
 for all \(\mathsf{u},\mathsf{v},\mathsf{w} \in \mathsf {S}\).
for all \(\mathsf{u},\mathsf{v},\mathsf{w} \in \mathsf {S}\).
In this case,  is a dislocated b-metric space (shortly
is a dislocated b-metric space (shortly  -MS).
-MS).
We mention that, when \(\mathsf {s}=1\), a  -MS becomes a
-MS becomes a  -MS.
-MS.
Definition 7
([36])
A sequence \(\{ \mathsf {v}_{n} \} \) on a  -MS
-MS  is said to be:
is said to be:
-
 -convergent to a point \(\mathsf {v}\in \mathsf {S}\) ⇔
-convergent to a point \(\mathsf {v}\in \mathsf {S}\) ⇔ 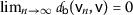 ;
; -
 -Cauchy if and only if
-Cauchy if and only if  exists and tends to be finite.
exists and tends to be finite.
Proposition 8
([36])
In a  -MS the limit of a convergent sequence is unique.
-MS the limit of a convergent sequence is unique.
Proposition 9
([36])
In a  -MS every convergent sequence is
-MS every convergent sequence is  -Cauchy.
-Cauchy.
In case every  -Cauchy sequence is
-Cauchy sequence is  -convergent, we say that the space
-convergent, we say that the space  is a complete
is a complete  -MS. The next lemma will be useful in the sequel.
-MS. The next lemma will be useful in the sequel.
Lemma 10
Let a  -MS
-MS  , a mapping
, a mapping  , and \(\mathsf {v}_{0}\) be arbitrary, but fixed point in S. If there exists \(\mathcal{C}\in [ 0,1 ) \) such that
, and \(\mathsf {v}_{0}\) be arbitrary, but fixed point in S. If there exists \(\mathcal{C}\in [ 0,1 ) \) such that

for every \(n\in \mathbb{N}\), then the sequence  is a
is a  -Cauchy sequence.
-Cauchy sequence.
Proof
Let \(\mathsf {v}_{0}\) be an arbitrary point in S and the sequence \(\{ \mathsf {v}_{n} \} \) with

for \(n\in \mathbb{N}\cup \{ 0 \} \). Thus, by (3), we have

We split the proof in two cases, namely \(\mathsf {s}=1\) and \(\mathsf {s}>1\).
-
1.
For \(\mathsf {s}=1\),
 becomes a dislocated metric and by
becomes a dislocated metric and by  ., for \(n< p\), we have
., for \(n< p\), we have 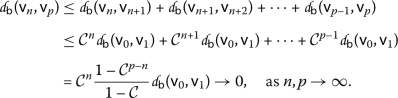
Therefore,
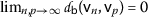 , that is, the sequence
, that is, the sequence 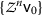 is Cauchy.
is Cauchy. -
2.
For \(\mathsf {s}>1\), we distinguish two sub-cases:
-
(a)
If \(\mathcal{C}\in [0,\frac{1}{\mathsf {s}})\), by
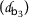 and taking into account (4), we get
and taking into account (4), we get 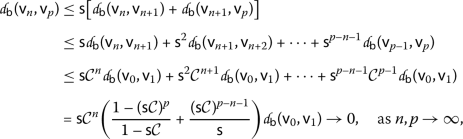
that is,
 is
is  -Cauchy.
-Cauchy. -
(b)
If \(\mathcal{C}\in [\frac{1}{\mathsf {s}},1)\), then \(\mathcal{C}^{n}\rightarrow 0\), and we can find \(l\in \mathbb{N}\) such that \(\mathcal{C}^{n}<\frac{1}{\mathsf {s}}\). Therefore, by (a), the sequence
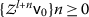 is
is  -Cauchy. But we have $$\begin{aligned} \{ \mathsf {v}_{n} \} = \{ \mathsf {v}_{0}, \mathsf {v}_{1},\ldots, \mathsf {v}_{l-1} \} \cup \{ \mathsf {v}_{l}, \mathsf {v}_{l+1},\ldots, \mathsf {v}_{l+n},\ldots \}, \end{aligned}$$
-Cauchy. But we have $$\begin{aligned} \{ \mathsf {v}_{n} \} = \{ \mathsf {v}_{0}, \mathsf {v}_{1},\ldots, \mathsf {v}_{l-1} \} \cup \{ \mathsf {v}_{l}, \mathsf {v}_{l+1},\ldots, \mathsf {v}_{l+n},\ldots \}, \end{aligned}$$and then the sequence
 is
is 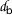 -Cauchy.
-Cauchy.
-
(a)
□
2 Main results
Henceforth, we use the following notations:
and, respectively,

Let the functions \(R_{1}, R_{2}:\mathsf {S}\times \mathsf {S}\rightarrow [0,\infty )\) be defined by

where  are nonnegative real numbers.
are nonnegative real numbers.
Theorem 11
Let  be a complete
be a complete  -ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and two continuous mappings
-ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and two continuous mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds. Assume that:
- \((\beta _{1})\):
-
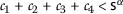 and
and 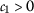 ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Proof
For an arbitrary (but fixed) point \(\mathsf {v}_{0}\in \mathsf {S}\), let \(\{ \mathsf {v}_{n} \} \) be the sequence defined as follows:

for all \(n\in \mathbb{N}_{0}\). First of all, we claim that \(\mathsf {v}_{n}\neq \mathsf {v}_{n+1}\) for any \(n\in \mathbb{N}_{0}\). Indeed, if we can find \(l_{0}\in \mathbb{N}\) such that \(\mathsf {v}_{l_{0}}=\mathsf {v}_{l_{0}+1}=\mathsf {v}_{l_{0}+2}=\mathsf {x}\), then  .
.
Under this assumption,  and letting \(\mathsf {v}=\mathsf {v}_{2n}\) and \(\mathsf {w}=\mathsf {v}_{2n+1}\) in (5), because the functions \(\Psi, \Phi \) belong to Θ, we have
and letting \(\mathsf {v}=\mathsf {v}_{2n}\) and \(\mathsf {w}=\mathsf {v}_{2n+1}\) in (5), because the functions \(\Psi, \Phi \) belong to Θ, we have

Taking (\(\beta _{1}\)) into account, we get

or

where  , holds due to the first assumption in \((\beta _{1})\).
, holds due to the first assumption in \((\beta _{1})\).
In the same way, replacing in (5) v with \(\mathsf {v}_{2n-1}\) and w with \(\mathsf {v}_{2n}\), and keeping in mind  , we have
, we have

which leads us to

Consequently, (7) and (9) show us that

for any \(n\in \mathbb{N}\), where  . By Lemma 10 it follows that \(\{ \mathsf {v}_{n} \} \) is a Cauchy sequence. Thus,
. By Lemma 10 it follows that \(\{ \mathsf {v}_{n} \} \) is a Cauchy sequence. Thus,  exists and is finite. Moreover, since the
exists and is finite. Moreover, since the  -ms is complete, we get that there exists \(\mathsf {x}\in \mathsf {S}\) such that \(\lim_{n\rightarrow \infty }\mathsf {v}_{n}=\mathsf {x}\) and
-ms is complete, we get that there exists \(\mathsf {x}\in \mathsf {S}\) such that \(\lim_{n\rightarrow \infty }\mathsf {v}_{n}=\mathsf {x}\) and

Since the mappings  and
and  are supposed to be continuous, we have
are supposed to be continuous, we have

that is,  . If we suppose that there exist
. If we suppose that there exist  such that \(\mathsf {x}\neq \mathsf {y}\), by (5) and since \(\Psi, \Phi \in \Theta \), we have
such that \(\mathsf {x}\neq \mathsf {y}\), by (5) and since \(\Psi, \Phi \in \Theta \), we have

where

However, applying  and taking into account
and taking into account  ,
,

Moreover, by \((\beta _{2})\) we get

which is a contradiction. Therefore,  and from
and from  it follows that \(\mathsf {x}=\mathsf {y}\), that is, the set
it follows that \(\mathsf {x}=\mathsf {y}\), that is, the set  has exactly one element. □
has exactly one element. □
Corollary 12
Let  be a complete
be a complete  -ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and a continuous mapping
-ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and a continuous mapping  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds, where for  nonnegative real numbers,
nonnegative real numbers,

for all \(\mathsf {v},\mathsf {w}\in \mathsf {S}, \mathsf {v}\neq \mathsf {w}\). Assume that:
- \((\beta _{1})\):
-
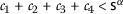 and
and  ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Proof
Let  in Theorem 11. □
in Theorem 11. □
Theorem 13
Let  be a complete
be a complete  -ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and two mappings
-ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and two mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds. Assume that:
- \((\beta _{1})\):
-
 ,
,  ,
, 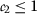 ,
, 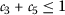 ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Proof
Let \(\mathsf {v}_{0}\in \mathsf {S}\) be a chosen point and \(\{ \mathsf {v}_{n} \} \) be the sequence defined by (6) in the proof of Theorem 11. Thus, following the same arguments, we can assume that  and from (13) we get
and from (13) we get

Since by \((\beta _{2})\) Ψ is nondecreasing, we deduce that

which is equivalent to

where  by \((\beta _{1})\). Similarly, taking \(\mathsf {v}=\mathsf {v}_{2n}\) and \(\mathsf {w}=\mathsf {v}_{2n-1}\) in (5) and keeping in mind
by \((\beta _{1})\). Similarly, taking \(\mathsf {v}=\mathsf {v}_{2n}\) and \(\mathsf {w}=\mathsf {v}_{2n-1}\) in (5) and keeping in mind  , we get
, we get

However, from relations (14), (15), together with Lemma 10, we find that \(\{ \mathsf {v}_{n} \} \) is a Cauchy sequence in a complete  -ms. Therefore, there exists \(\mathsf {x}\in \mathsf {S}\) such that
-ms. Therefore, there exists \(\mathsf {x}\in \mathsf {S}\) such that

Without loss of generality, we can suppose that \(\mathsf {x}\neq \mathsf {v}_{n}\) for any \(n\in \mathbb{N}\). Supposing that  , by (5), we have
, by (5), we have

or, taking \((\beta _{2})\) into account,

However, since

we obtain

On the other hand,

and then

which contradicts our assumption  . Thus, we get
. Thus, we get  , that is,
, that is,  . Moreover, if we suppose that
. Moreover, if we suppose that  , since
, since  ,
,

or, keeping in mind \((\beta _{2})\)

which is a contradiction. Therefore,  which implies by
which implies by  that
that  . That is,
. That is,  .
.
As a last step, we claim that x is the unique fixed point of the mappings  and
and  . Indeed, if we suppose that there exists another point
. Indeed, if we suppose that there exists another point  such that \(\mathsf {x}\neq \upsilon \), by (13) we have
such that \(\mathsf {x}\neq \upsilon \), by (13) we have

Since the function Ψ is supposed to be nondecreasing, it follows that

which is a contradiction. Therefore, the set  has exactly one element. □
has exactly one element. □
Corollary 14
Let  be a complete
be a complete  -ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and a mapping
-ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\), and a mapping  such that, for every \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds, where for  nonnegative real numbers,
nonnegative real numbers,

Assume that:
- \((\beta _{1})\):
-
 ,
, 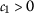 , and
, and 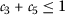 ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Proof
Let  in Theorem 13. □
in Theorem 13. □
Example 15
Let the set  and the function
and the function  be defined by
be defined by
| m | n | p | q |
|---|---|---|---|---|
m | 0 | 2 | 5 | 7 |
n | 2 | 6 | 8 | 5 |
p | 5 | 8 | 0 | 1 |
q | 7 | 5 | 1 | 0 |
Obviously,  is a
is a  -metric, with \(\mathsf {s}=2\). Let
-metric, with \(\mathsf {s}=2\). Let  be two mappings, where
be two mappings, where  and
and  . We have, in this case,
. We have, in this case,
v | m | n | p | q |
|---|---|---|---|---|
| p | q | p | p |
| q | q | p | p |
| 5 | 5 | 0 | 1 |
| 7 | 5 | 0 | 1 |
v | m | n | p | q | ||
|---|---|---|---|---|---|---|
|
| p | q | p | p | |
w |
| |||||
m | q | 1 | 0 | 1 | 1 | |
n | q | 1 | 0 | 1 | 1 | |
p | p | 0 | 1 | 0 | 0 | |
q | p | 0 | 1 | 0 | 0 |
Letting the functions \(\Psi, \Phi \in \Theta \), \(\Psi (\theta )=\theta \), \(\Phi (\theta )=\frac{3}{4}\theta \) and the numbers \(\alpha =2\),  ,
,  ,
,  , we can easily see that assumptions \((\beta _{1})\) and \((\beta _{2})\) in Theorem 13 are satisfied. We show that (13) is satisfied for any pair
, we can easily see that assumptions \((\beta _{1})\) and \((\beta _{2})\) in Theorem 13 are satisfied. We show that (13) is satisfied for any pair  , where
, where

(the other cases are excluded by the hypotheses of Theorem 13).
-
\((\mathsf {v},\mathsf {w})=(m,n)\)
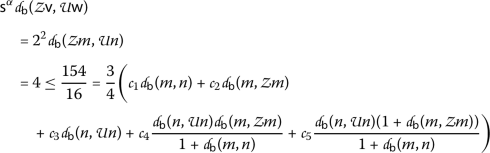
-
\((\mathsf {v},\mathsf {w})=(n,p)\)
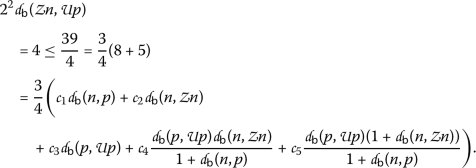
The other cases are discussed similarly.
Thus  .
.
Theorem 16
Let  be a complete
be a complete  -ms, the functions \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\),
-ms, the functions \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\),  , and two mappings
, and two mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds, where

Assume that:
- \((\beta _{1})\):
-
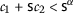 ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then the set  has exactly one element.
has exactly one element.
Proof
Let us take in (20), \(\mathsf {v}=\mathsf {v}_{2n}\) and \(\mathsf {w}=\mathsf {v}_{2n+1}\), where the sequence \(\{ \mathsf {v}_{n} \} \) is defined as in Theorem 11. We have

with

Furthermore, taking \((\beta _{2})\) and the above relation into account, we get

which implies

Similarly, taking \(\mathsf {v}=\mathsf {v}_{2n}\), respectively \(\mathsf {w}=\mathsf {v}_{2n-1}\), we obtain

Now, choosing  (by assumption \((\beta _{1})\)), we have
(by assumption \((\beta _{1})\)), we have  for any \(n\in \mathbb{N}\). Therefore, Lemma 10 leads us to the conclusion that \(\{ \mathsf {v}_{n} \} \) is a Cauchy sequence. Thus, since the space is complete, there exists \(\mathsf {x}\in \mathsf {S}\) such that
for any \(n\in \mathbb{N}\). Therefore, Lemma 10 leads us to the conclusion that \(\{ \mathsf {v}_{n} \} \) is a Cauchy sequence. Thus, since the space is complete, there exists \(\mathsf {x}\in \mathsf {S}\) such that

Supposing that  , we have
, we have

Moreover, without loss of generality, we can assume that  for any \(n\in \mathbb{N}\), and then from (20) we get
for any \(n\in \mathbb{N}\), and then from (20) we get

or, by \((\beta _{2})\),

Returning in (25), we have

Letting \(n\rightarrow \infty \) and keeping in mind (24), we get

which is a contradiction. Thus,  and from
and from  we have
we have  .
.
Analogously, we have

or, by \((\beta _{2})\),

On the other hand, supposing that  , we have
, we have

Combining the above inequalities and taking limit as \(n\rightarrow \infty \), we obtain  , which is a contradiction. Therefore,
, which is a contradiction. Therefore,  , and then
, and then  . Thus, x is a common fixed point for
. Thus, x is a common fixed point for  and
and  , that is,
, that is,  and it remains to show that the set
and it remains to show that the set  is in fact reduced to a single point. On the contrary, let
is in fact reduced to a single point. On the contrary, let  with \(\upsilon \neq \mathsf {x}\). Replaced in (20), we have
with \(\upsilon \neq \mathsf {x}\). Replaced in (20), we have

and, due to \((\beta _{2})\),

which is a contradiction. Therefore, it follows that \(\mathsf {x}=\upsilon \) and the set  has exactly one element. □
has exactly one element. □
Example 17
Let \(\mathsf {S}= \{ 2,4,5,7 \} \) and two self-mappings  be defined on S by
be defined on S by
v | 2 | 4 | 5 | 7 |
|---|---|---|---|---|
| 5 | 5 | 5 | 4 |
| 4 | 5 | 5 | 5 |
Let  be the
be the  -metric on S (with \(\mathsf {s}=2\)) given by
-metric on S (with \(\mathsf {s}=2\)) given by

Considering the functions \(\Psi, \Phi \in \Theta \) as in Example (15) and letting \(\alpha =2\),  ,
,  , we have the following cases:
, we have the following cases:
-
\((\mathsf {v}, \mathsf {w})=(4,2)\)

-
\((\mathsf {v}, \mathsf {w})=(5,2)\)
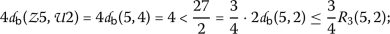
-
\((\mathsf {v}, \mathsf {w})=(7,2)\)
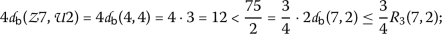
-
\((\mathsf {v}, \mathsf {w})=(7,4)\)
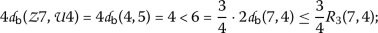
-
\((\mathsf {v}, \mathsf {w})=(7,5)\)

The other cases are excluded by the hypothesis of Theorem 16. Therefore,  .
.
Corollary 18
Let  be a complete
be a complete  -ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\),
-ms, \(\Psi, \Phi \in \Theta \), a number \(\alpha \in [1,\infty )\),  , and a mapping
, and a mapping  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds, where

Assume that:
- \((\beta _{1})\):
-
 ;
; - \((\beta _{2})\):
-
Ψ is nondecreasing.
Then the set  has exactly one element.
has exactly one element.
Proof
Let  in Theorem 16. □
in Theorem 16. □
3 Consequences
Taking particular functions Ψ and Φ, we obtain as consequences some known results. For example, let \(\Phi (\theta )=\beta (\theta )\Psi (\theta )\) for all \(\theta >0\) and \(\beta:[0,\infty )\rightarrow [0,\frac{1}{\mathsf {s}})\).
Corollary 19
Let  be a complete
be a complete  -ms, a number \(\alpha \in [1,\infty )\), and two continuous mappings
-ms, a number \(\alpha \in [1,\infty )\), and two continuous mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds. Assume that:
- \((\beta _{1})\):
-
 and
and  ;
; - \((\beta _{3})\):
-
\(\Psi:(0,\infty )\rightarrow (0,\infty )\) is nondecreasing;
- \((\beta _{4})\):
-
\(\beta:(0,\infty )\rightarrow (0,\frac{1}{\mathsf {s}})\) satisfies \(\limsup_{\theta \rightarrow \theta _{0}}\beta ( \theta )<\frac{1}{\mathsf {s}}\) for any \(\theta _{0}>0\).
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Corollary 20
Let  be a complete
be a complete  -ms, a number \(\alpha \in [1,\infty )\), and two mappings
-ms, a number \(\alpha \in [1,\infty )\), and two mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds. Assume that:
- \((\beta _{1})\):
-
 ,
, 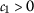 ,
,  , and
, and 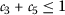 ;
; - \((\beta _{3})\):
-
\(\Psi:(0,\infty )\rightarrow (0,\infty )\) is nondecreasing;
- \((\beta _{4})\):
-
\(\beta:(0,\infty )\rightarrow (0,\frac{1}{\mathsf {s}})\) satisfies \(\limsup_{\theta \rightarrow \theta _{0}}\beta ( \theta )<\frac{1}{\mathsf {s}}\) for any \(\theta _{0}>0\).
Then  . Moreover, if
. Moreover, if  , then the set
, then the set  has exactly one element.
has exactly one element.
Corollary 21
Let  be a complete
be a complete  -ms, a number \(\alpha \in [1,\infty )\), and two mappings
-ms, a number \(\alpha \in [1,\infty )\), and two mappings  such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with
such that, for every distinct \(\mathsf {v}, \mathsf {w}\in \mathsf {S}\) with  , the following inequality
, the following inequality

holds. Assume that:
- \((\beta _{1})\):
-
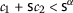 ,
, 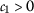 ;
; - \((\beta _{3})\):
-
\(\Psi:(0,\infty )\rightarrow (0,\infty )\) is nondecreasing;
- \((\beta _{4})\):
-
\(\beta:(0,\infty )\rightarrow (0,\frac{1}{\mathsf {s}})\) satisfies \(\limsup_{\theta \rightarrow \theta _{0}}\beta ( \theta )<\frac{1}{\mathsf {s}}\) for any \(\theta _{0}>0\).
Then the set  has exactly one element.
has exactly one element.
Considering \(\Phi (\theta )=\kappa \Psi (\theta )\) or \(\Phi (\theta )=\kappa \cdot \theta \) for all \(\theta >0\) in Theorems 11, 13 or 16, other consequences can be listed. On the other hand, many other corollaries can be deduced considering  or letting \(\mathsf {s}=1\).
or letting \(\mathsf {s}=1\).
Availability of data and materials
The data and material used to support the findings of this study are included within the article.
References
Afshari, H., Aydi, H., Karapınar, E.: On generalized α-ψ-Geraghty contractions on b-metric spaces. Georgian Math. J. 27, 9–21 (2020)
Alghamdi, M.A., Gulyaz-Ozyurt, S., Karapınar, E.: A note on extended Z-contraction. Mathematics 2020(8), 195 (2020)
Alsulami, H., Gulyaz, S., Karapınar, E., Erhan, İ.: An Ulam stability result on quasi-b-metric-like spaces. Open Math. (2016). https://doi.org/10.1515/math-2016-0097
Aksoy, Ü., Karapınar, E., Erhan, İ.M.: Fixed points of generalized α-admissible contractions on b-metric spaces with an application to boundary value problems. J. Nonlinear Convex Anal. 17, 1095–1108 (2016)
Aydi, H., Karapınar, E., Bota, M.F., Mitrović, S.: A fixed point theorem for set-valued quasi-contractions in b-metric spaces. Fixed Point Theory Appl. 2012, 88 (2012)
Aydi, H., Bota, M.F., Karapınar, E., Moradi, S.: A common fixed point for weak ϕ-contractions on b-metric spaces. Fixed Point Theory 13, 337–346 (2012)
Fulga, A., Karapınar, E., Petruşel, G.: On hybrid contractions in the context of quasi-metric spaces. Mathematics 2020(8), 675 (2020)
Gulyaz-Ozyurt, S.: On some α-admissible contraction mappings on Branciari b-metric spaces. Adv. Theor. Nonlinear Anal. Appl. 1, 1–13 (2017)
Karapınar, E., Chifu, C.: Results in wt-distance over b-metric spaces. Mathematics 2020(8), 220 (2020)
Karapınar, E., Fulga, A., Petruşel, A.: On Istratescu type contractions in b-metric spaces. Mathematics 2020(8), 388 (2020)
Marasi, H.R., Aydi, H.: Existence and uniqueness results for two-term nonlinear fractional differential equations via a fixed point technique. J. Math. 2021, Article ID 6670176 (2021)
Javed, K., Aydi, H., Uddin, F., Arshad, M.: On orthogonal partial b-metric spaces with an application. J. Math. 2021, Article ID 6692063 (2021)
Mlaiki, N., Souayah, N., Abdeljawad, T., Aydi, H.: A new extension to the controlled metric type spaces endowed with a graph. Adv. Differ. Equ. 2021(2021), 94 (2021)
Hammad, H.A., Aydi, H., Mlaiki, N.: Contributions of the fixed point technique to solve the 2D Volterra integral equations, Riemann–Liouville fractional integrals, and Atangana–Baleanu integral operators. Adv. Differ. Equ. 2021(2021), 97 (2021)
Aydi, H., Lakzian, H., Mitrović, Z.D., Radenović, S.: Best proximity points of MT-cyclic contractions with property UC. Numer. Funct. Anal. Optim. 41(7), 871–882 (2020)
Karapınar, E., Czerwik, S., Aydi, H.: \((\alpha,\psi )\)-Meir–Keeler contraction mappings in generalized b-metric spaces. J. Funct. Spaces 2018, Article ID 3264620 (2018)
Alqahtani, B., Fulga, A., Karapınar, E., Kumari, P.S.: Sehgal type contractions on dislocated spaces. Mathematics 2019(7), 153 (2019)
Gholizadeh, L., Karapınar, E.: Best proximity point results in dislocated metric spaces via R-functions. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 112, 1391–1407 (2018)
Karapınar, E.: A note on Meir–Keeler contractions on dislocated quasi-b-metric. Filomat 31, 4305–4318 (2017)
Karapınar, E., Salimi, P.: Dislocated metric space to metric spaces with some fixed point theorems. Fixed Point Theory Appl. 2013(2013), 222 (2013)
Karapınar, E.: A short survey on dislocated metric spaces via fixed point theory. In: Banas, J., et al. (eds.) Advances in Nonlinear Analysis via the Concept of Measure of Noncompactness, pp. 457–483. Springer, Berlin (2017)
Chen, C., Dong, J., Zhu, C.: Some fixed point theorems in b-metric-like spaces. Fixed Point Theory Appl. 2015(2015), 122 (2015)
Rahman, M.U., Sarwar, M.: Dislocated quasi b-metric space and fixed point theorems. Electron. J. Math. Anal. Appl. 4, 16–24 (2016)
Shahzad, N., Roldán López de Hierro, A.F., Khojasteh, F.: Some new fixed point theorems under (\(\mathcal{A}\), \(\mathcal{S}\))-contractivity conditions. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111, 307–324 (2017)
Adigüzel, R.S., Aksoy, Ü., Karapınar, E., Erhan, İ.M.: On the solution of a boundary value problem associated with a fractional differential equation. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6652
Al-Mezel, S.A., Alsulami, H.H., Karapınar, E., Roldán López de Hierro, A.F.: Discussion on “multidimensional coincidence points” via recent publications. Abstr. Appl. Anal. 2014, Article ID 287492 (2015)
Roldán López de Hierro, A.F., Karapınar, E., Manro, S.: Some new fixed point theorems in fuzzy metric spaces. J. Intell. Fuzzy Syst. 27, 2257–2264 (2014)
Proinov, P.D.: Fixed point theorems for generalized contractive mappings in metric spaces. J. Fixed Point Theory Appl. 22, Article ID 21 (2020)
Wardowski, D.: Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 94 (2012)
Jleli, M., Samet, B.: A new generalization of the Banach contraction principle. J. Inequal. Appl. 38, 1–8 (2014)
Karapınar, E., Roldán, A., Sadarangani, K.: Existence and uniqueness of best proximity points under rational contractivity conditions. Math. Slovaca 66, 1427–1442 (2016)
Dass, B.K., Gupta, S.: An extension of Banach contraction principle through rational expressions. Indian J. Pure Appl. Math. 6, 1455–1458 (1975)
Jaggi, D.S.: Some unique fixed point theorems. Indian J. Pure Appl. Math. 8, 223–230 (1977)
Hitzler, P., Seda, A.K.: Dislocated topologies. J. Electr. Eng. 51, 3–7 (2000)
Czerwik, S.: Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1, 5–11 (1993)
Hussain, N., Roshan, J.R., Parvaneh, V., Abbas, M.: Common fixed point results for weak contractive mappings in ordered b-dislocated metric spaces with applications. J. Inequal. Appl. 2013(2013), 486 (2013)
Acknowledgements
The authors thank their universities. The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no. RG-1437-037. A.F. Roldán López de Hierro is grateful to Project TIN2017-89517-P of Ministerio de Economía, Industria y Competitividad and also to Junta de Andalucía by project FQM-365 of the Andalusian CICYE.
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
The authors carried out the whole manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alqahtani, B., Alzaid, S.S., Fulga, A. et al. Proinov type contractions on dislocated b-metric spaces. Adv Differ Equ 2021, 164 (2021). https://doi.org/10.1186/s13662-021-03329-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03329-5
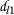 .:
.: .:
.: .:
.: .:
.: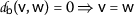 ;
; .:
.: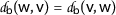 ;
; .:
.: for all
for all  -convergent to a point
-convergent to a point 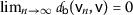 ;
; -Cauchy if and only if
-Cauchy if and only if  exists and tends to be finite.
exists and tends to be finite. becomes a dislocated metric and by
becomes a dislocated metric and by  ., for
., for 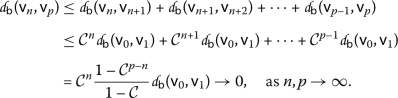
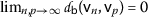 , that is, the sequence
, that is, the sequence  is Cauchy.
is Cauchy. and taking into account (
and taking into account (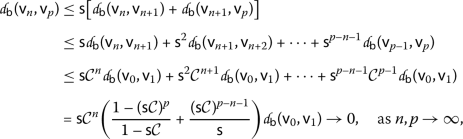
 is
is  -Cauchy.
-Cauchy.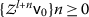 is
is  -Cauchy. But we have
-Cauchy. But we have  is
is 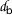 -Cauchy.
-Cauchy.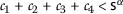 and
and 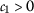 ;
;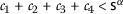 and
and  ;
; ,
,  ,
, 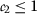 ,
, 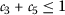 ;
; ,
, 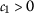 , and
, and 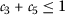 ;
;







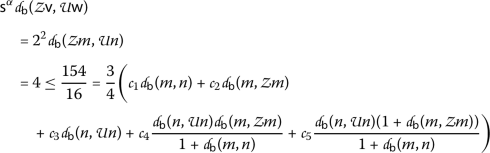
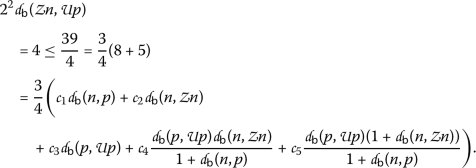
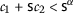 ;
;


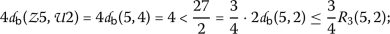
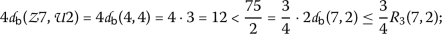
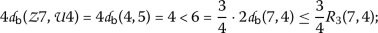

 ;
; and
and  ;
; ,
, 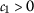 ,
,  , and
, and 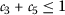 ;
;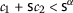 ,
, 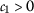 ;
;