- Research
- Open access
- Published:
A parallel hybrid accelerated extragradient algorithm for pseudomonotone equilibrium, fixed point, and split null point problems
Advances in Difference Equations volume 2021, Article number: 364 (2021)
Abstract
This paper provides iterative construction of a common solution associated with the classes of equilibrium problems (EP) and split convex feasibility problems. In particular, we are interested in the EP defined with respect to the pseudomonotone bifunction, the fixed point problem (FPP) for a finite family of  -demicontractive operators, and the split null point problem. From the numerical standpoint, combining various classical iterative algorithms to study two or more abstract problems is a fascinating field of research. We, therefore, propose an iterative algorithm that combines the parallel hybrid extragradient algorithm with the inertial extrapolation technique. The analysis of the proposed algorithm comprises theoretical results concerning strong convergence under a suitable set of constraints and numerical results.
-demicontractive operators, and the split null point problem. From the numerical standpoint, combining various classical iterative algorithms to study two or more abstract problems is a fascinating field of research. We, therefore, propose an iterative algorithm that combines the parallel hybrid extragradient algorithm with the inertial extrapolation technique. The analysis of the proposed algorithm comprises theoretical results concerning strong convergence under a suitable set of constraints and numerical results.
1 Introduction
The class of convex feasibility problems (CFP) has been widely studied in the current literature as it encompasses a variety of problems arising in mathematical and physical sciences. Numerous iterative algorithms have been studied to obtain an approximate solution for the CFP in Hilbert spaces. However, the class of projection algorithms is prominent among various iterative algorithms to solve the CFP. It is remarked that the class of CFP is closely related to the theory of convex optimization and hence monotone operator theory. As a consequence, CFP found valuable applications in the field of partial differential equations, image recovery problem, approximation theory, signal and image processing through projection algorithms, control problems, evolution equations and inclusions, see for instance [6, 15, 16] and the references cited therein.
The class of CFP has been generalized in several ways. One of the elegant modifications and generalizations of the CFP is the split convex feasibility problems (SCFP) proposed by Censor and Elfving [12]. The mathematical formulation of the SCFP opens up an interesting framework to model the medical image reconstruction problem and the intensity-modulated radiation therapy [8, 11]. As a consequence, the SCFP has been studied extensively in the current literature with possible real-world applications, see for example [9, 11, 13, 14, 19] and the references cited therein. Recall that a SCFP deals with a model aiming to find a point
such that
where \(\hbar:\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}\) is a bounded linear operator between two real Hilbert spaces \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\).
Since the introduction of SCFP, various important instances of SCFP have been introduced and analyzed such as the split variational inequality problem [13], the split common null point problem (SCNPP) [9], the split common FPP [14], and the split equilibrium problem [7]. We are interested in studying the SCNPP, one of the important instances of SCFP, defined as follows:
Given two multivalued operators \(A_{1}:\mathcal{H}_{1}\rightarrow 2^{\mathcal{H}_{1}}\) and \(A_{2}:\mathcal{H}_{2}\rightarrow 2^{\mathcal{H}_{2}}\), the SCNPP problem deals with a model aiming to find a point
In 2012, Byrne et al. [9] suggested the following iterative schemes to solve the SCNPP (3) associated with two maximal monotone operators \(A_{1}\) and \(A_{2}\):
and
where \(\hbar ^{*}\) denotes the adjoint operator of ħ, Id denotes the identity operator and \(J_{m}^{A_{1}},J_{m}^{A_{2}}\) denote the corresponding resolvents of \(A_{1},A_{2}\), respectively. The set of solutions of the SCNPP (3) is denoted by \(\Omega:=\{\bar{x} \in A^{-1}_{1}(0):\hbar \bar{x} \in A^{-1}_{2}(0) \}\). It is remarked that the scheme (4) exhibits weak convergence, while the scheme (5) exhibits strong convergence under suitable sets of constraints.
In 1994, Blum and Oettli [7] proposed, in a mathematical formulation, an EP with respect to a (monotone) bifunction g defined on a nonempty subset C of a real Hilbert space \(\mathcal{H}_{1}\) that aims to find a point \(\bar{x}\in C\) such that
The set of equilibrium points or solutions of the problem (6) is denoted by \(EP(g)\).
In 2006, Tada and Takahashi [29] suggested a hybrid algorithm for the analysis of monotone EP and FPP in Hilbert spaces. Nevertheless, the iterative algorithm proposed in [29] fails for the case of pseudomonotone EP. In order to address this issue, Anh [2] suggested a hybrid extragradient method, based on the seminal work of Korpelevich [23], in Hilbert spaces. Inspired by the work of Anh [2], Hieu et al. [20] suggested a parallel hybrid extragradient framework to address pseudomonotone EP together with the FPP. In 2015, Takahashi et al. [30] constructed a common solution of the zero point problem and FPP. Therefore, it is natural to study the pseudomonotone EP and the SCNPP with the FPP associated with a more general class of demicontractive operators.
It is remarked that the computational performance of an iterative algorithm can be enhanced by employing different techniques. The parallel architecture of an iterative algorithm reduces the computational cost, whereas the inertial extrapolation technique [26] provides fast convergence characteristics of the algorithm. The latter technique has successfully been combined with different classical iterative algorithms, see for example [1, 3–5, 10, 18, 21, 22, 25, 32] and the references cited therein. We, therefore, study the convergence analysis of a variant of parallel hybrid extragradient iterative algorithm embedded with the inertial extrapolation technique in Hilbert spaces.
The rest of the paper is organized as follows: Sect. 2 contains some relevant preliminary concepts and results for (split) monotone operator theory, EP theory, and fixed point theory. Section 3 comprises strong convergence results, whereas Sect. 4 provides numerical results concerning the viability of the proposed algorithm with respect to various real world applications.
2 Preliminaries
We first define some necessary notions from fixed point theory. Let \(T:C\rightarrow C\) be an operator defined on a nonempty subset C of a real Hilbert space \(\mathcal{H}_{1}\), then T is known as nonexpansive if \(\Vert Tx-Ty\Vert \leq \Vert x-y\Vert \) for all \(x,y\in C\). Further, T is known as firmly nonexpansive if
Moreover, the operator T is defined as  -demicontractive if \(\mathrm{Fix}(T)\neq \emptyset \), and there exists
-demicontractive if \(\mathrm{Fix}(T)\neq \emptyset \), and there exists  such that
such that

where \(\mathrm{Fix}(T)= \{ x\in C:x-Tx=0 \} \) denotes the set of all fixed points of the operator T. Note that the operator \(\mathrm{Id}-T\) is said to be demiclosed at the origin if for any sequence \((x_{k})\) in a nonempty closed and convex subset C of \(\mathcal{H}_{1}\) converges weakly to some x and if \(((\mathrm{Id}-T)x_{k})\) converges strongly to 0, then \((\mathrm{Id}-T)(x)=0\). It is remarked that, for each \(x\in \mathcal{H}_{1}\), there exists unique \(P_{C}x\in C\) satisfying \(\Vert x-P_{C}x\Vert \leq \Vert x-z\Vert \text{ for all } z\in C\). Such an operator \(P_{C}:\mathcal{H}_{1}\rightarrow C\) is coined as metric projection and satisfies \(\langle x-P_{C}x,P_{C}x-y\rangle \geq 0,\text{ for all } x\in \mathcal{H}_{1}\text{ and }y\in C\).
We now state a brief introductory material covering monotone operator theory from the celebrated monograph of Bauschke and Combettes [6].
For a set-valued operator \(A_{1}:\mathcal{H}_{1}\rightarrow 2^{\mathcal{H}_{1}}\), the following sets \(\operatorname{dom}(A_{1})=\{x\in \mathcal{H}_{1} | A_{1}x\neq \emptyset \}\), \(\operatorname{ran}(A_{1})=\{u\in \mathcal{H}_{1} | (\exists x\in \mathcal{H}_{1}) u\in A_{1}x\}\), \(\operatorname{gra}(A_{1})=\{(x,u)\in \mathcal{H}_{1}\times \mathcal{H}_{1} | u\in A_{1}x\}\), and \(\operatorname{zer}(A_{1})=\{x\in \mathcal{H}_{1} | 0\in A_{1}x\}\) define and denote the domain, range, graph, and zeros of \(A_{1}\), respectively. The inverse operator \(A_{1}^{-1}\) of \(A_{1}\) can be defined as
The set-valued operator \(A_{1}\) is said to be monotone if \(\langle x-y,u-v\rangle \geq 0\) for all \((x,u),(y,v)\in \operatorname{gra}(A_{1})\). A monotone operator \(A_{1}\) is coined as maximal monotone operator if there is no proper monotone extension of \(A_{1}\), equivalently if \(\operatorname{ran}(\mathrm{Id}+mA_{1})=\mathcal{H}_{1}\) for all \(m>0\). An important notion associated with the monotone operator \(A_{1}\) is the well-defined resolvent operator \(J_{m}^{A_{1}}=(\mathrm{Id}+mA_{1})^{-1}\). Such an operator is single-valued and satisfies nonexpansiveness as well as \(\mathrm{Fix}(J_{m}^{A_{1}})=A_{1}^{-1}(0)\) for all \(m>0\).
The rest of this section is organized with celebrated results required in the sequel.
Assumption 2.1
Let \(g:C\times C\rightarrow \mathbb{R}\cup \{+\infty \}\) be a bifunction satisfying the following assumptions:
(A1): g is pseudomonotone, i.e., \(g(x,y)\leq 0\Rightarrow g(x,y)\geq 0\text{ for all } x,y\in C\);
(A2): g is Lipschitz-type continuous, i.e., there exist two nonnegative constants \(d_{1},d_{2}\) such that
(A3): g is weakly continuous on \(C\times C\) implies that, if \(x,y \in C\) and \((x_{k}), (y_{k})\) are two sequences in C converging weakly to x and y, respectively, then \(g(x_{k},y_{k})\) converges to \(g(x,y)\);
(A4): For each fixed \(x\in C\), \(g(x,.)\) is convex and subdifferentiable on C.
It is remarked that the monotonicity of g, i.e., \(g(x,y)+g(y,x)\leq 0,\text{ for all }x,y\in C\) implies the pseudomonotonicity but the converse is not true in general. The following lemmas are helpful in proving the strong convergence results in the next section.
Lemma 2.2
Let \(x,y\in \mathcal{H}_{1}\) and \(\beta \in \mathbb{R}\), then
-
1.
\(\Vert x+y\Vert ^{2} \leq \Vert x \Vert ^{2}+2 \langle y, x+y \rangle \);
-
2.
\(\Vert x-y\Vert ^{2} \leq \Vert x \Vert ^{2}-\Vert y \Vert ^{2}-2 \langle x-y, y \rangle \);
-
3.
\(\|\beta x+(1-\beta )y\|^{2}=\beta \|x\|^{2}+(1-\beta )\|y\|^{2}- \beta (1-\beta )\|x-y\|^{2}\).
Lemma 2.3
([24])
Let C be a nonempty closed and convex subset of a real Hilbert space \(\mathcal{H}_{1}\). For every \(x,y,z\in \mathcal{H}_{1}\) and \(\gamma \in \mathbb{R}\), the set
is closed and convex.
Lemma 2.4
([31])
Let C be a nonempty closed and convex subset of a real Hilbert space \(\mathcal{H}_{1}\), and let \(h:C \rightarrow \mathbb{R}\) be a convex and subdifferentiable function on C. Then x̄ is the solution of convex problem \(\min \{h(x):x \in C\}\) if and only if \(0 \in \partial h(\bar{x})+N_{C}(\bar{x})\), where \(\partial h(\cdot )\) denotes the subdifferential of h and \(N_{C}(\bar{x})\) is the normal cone of C at x̄.
3 Algorithm and convergence analysis
We enlist standard necessary hypotheses for the main result of this section. Note that, for a finite family of pseudomonotone bifunctions \(g_{i}\), we can compute the same Lipschitz coefficients \((d_{1},d_{2})\) by employing Assumption 2.1(A2) as follows:
where \(d_{1}=\max_{1\leq i \leq M}\{d_{1,i}\}\) and \(d_{2}=\max_{1\leq i \leq M}\{d_{2,i}\}\). Therefore, \(g_{i}(x,y)+g_{i}(y,z)\geq g_{i}(x,z)-d_{1}\Vert x-y \Vert ^{2}-d_{2} \Vert y-z\Vert ^{2}\).
Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two real Hilbert spaces, and let \(C \subseteq \mathcal{H}_{1}\) be a nonempty, closed, and convex subset. Then
-
(H1)
Let \(A_{1}:\mathcal{H}_{1} \rightarrow 2^{\mathcal{H}_{1}}\), \(A_{2}:\mathcal{H}_{2} \rightarrow 2^{\mathcal{H}_{2}}\) be two maximal monotone operators, and for \(m,n>0\), let \(J^{A_{1}}_{m}\), \(J^{A_{2}}_{n}\) be the resolvents of \(A_{1}\) and \(A_{2}\), respectively;
-
(H2)
Let \(\hbar: \mathcal{H}_{1} \rightarrow \mathcal{H}_{2}\) be a bounded linear operator such that \(\hbar ^{\ast }\) is the adjoint operator of ħ;
-
(H3)
Let \(g_{i}:C\times C\rightarrow \mathbb{R}\cup \{+\infty \}\) be a finite family of bifunctions satisfying Assumption 2.1;
-
(H4)
Let \(S_{j}:\mathcal{H}_{1} \rightarrow \mathcal{H}_{1}\) be a finite family of
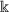 -demicontractive operators;
-demicontractive operators; -
(H5)
Assume that \(\Gamma:= \Omega \cap (\bigcap^{M}_{i=1}EP(g_{i}) ) \cap ( \bigcap^{N}_{j=1}\mathrm{Fix}(S_{j}) ) \neq \emptyset \).
Theorem 3.1
If \(\Gamma \neq \emptyset \), then the sequence \((x_{k})\) generated by Algorithm 1 converges strongly to an element in Γ, provided the following conditions hold:
-
(C1)
\(\sum^{\infty }_{k=1}\Theta _{k}\|x_{k}-x_{k-1}\|<\infty \);
-
(C2)
\(0 < a^{\ast } < \liminf_{k \rightarrow \infty } \alpha _{k} \leq \limsup_{k \rightarrow \infty } \alpha _{k} \leq b^{\ast } < 1\) and
 ;
; -
(C3)
\(\liminf_{k \rightarrow \infty } \beta _{k} > 0\);
-
(C4)
\(\liminf_{k \rightarrow \infty } m_{k} > 0\), \(\liminf_{k \rightarrow \infty } n_{k} > 0\).
Remark 3.2
We remark here that the condition (C1) is easily implementable in a numerical computation since the values of \(\|x_{k}-x_{k-1}\|\) are known before choosing \(\Theta _{k}\). The parameter \(\Theta _{k}\) can be taken as \(0 \leq \Theta _{k} \leq \widehat{\Theta _{k}}\),
where \(\{ \nu _{k}\}\) is a positive sequence such that \(\sum^{\infty }_{k = 1}\nu _{k} < \infty \) and \(\Theta \in [0,1)\).
We use the following result for the analysis of Algorithm 1.
Lemma 3.3
([27])
Suppose that \(\bar{x} \in EP(g_{i})\), and \(x_{k}\), \(b_{k}\), \(u^{i}_{k}\), \(w^{i}_{k}\), \(i \in \{1,2,\ldots,M\}\) are defined in Step 1 of Algorithm 1. Then we have
Proof of Theorem 3.1
The proof is divided into the following steps.
Step 1. We show that the sequence \(( x_{k})\) defined in Algorithm 1 is well defined.
We know that Γ is closed and convex. Moreover, from Lemma 2.3 we have that \(C_{k+1}\) is closed and convex for each \(k\geq 1\). Hence the projection \(P_{C_{k+1}}x_{1}\) is well defined. For any \(\bar{x}\in \Gamma \), observe that
Further

Furthermore,
Since \(J^{A_{1}}_{m_{k}}\) is nonexpansive, therefore the expression \(\Vert J^{A_{1}}_{m_{k}}(\bar{w}_{k}+\delta \hbar ^{\ast }(J^{A_{2}}_{n_{k}}-\mathrm{Id}) \hbar \bar{w}_{k})-\bar{x}\Vert ^{2}\) simplifies as follows:
Using \(J^{A_{2}}_{n_{k}}\) as firmly nonexpansive, we simplify the expression \(\lambda _{k}=2\delta \langle \hbar \bar{w}_{k}-\hbar \bar{x},(J^{A_{2}}_{n_{k}}-\mathrm{Id}) \hbar \bar{w}_{k} \rangle \) as follows:
Utilizing (10), (11), and Lemma 3.3, we then obtain from (9) that
It follows from (12) that
The above estimate (13) infers that \(\Gamma \subset C_{k+1}\). Hence, we conclude that Algorithm 1 is well defined.
Step 2. We show that the limit \(\lim_{k\rightarrow \infty }\Vert x_{k}-x_{1}\Vert \) exists.
Note that, for \(x_{k+1}=P_{C_{k+1}}x_{1}\), we have \(\Vert x_{k+1}-x_{1}\Vert \leq \Vert x^{\ast }-x_{1}\Vert \) for all \(x^{\ast }\in C_{k+1}\). In particular \(\Vert x_{k+1}-x_{1}\Vert \leq \Vert \bar{x}-x_{1}\Vert \) for all \(\bar{x}\in \Gamma \subset C_{k+1}\) This proves that the sequence \((\Vert x_{k}-x_{1}\Vert )\) is bounded. On the other hand, from \(x_{k}=P_{C_{k}}x_{1}\) and \(x_{k+1}=P_{C_{k+1}}x_{1}\in C_{k+1}\), we have
This implies that \((\Vert x_{k}-x_{1}\Vert )\) is nondecreasing, and hence
Step 3. We show that \(\bar{x_{*}}\in \Gamma \).
First, observe that
Taking limsup on both sides of the above estimate and utilizing (14), we have
\(\limsup_{k\rightarrow \infty } \Vert x_{k+1}-x_{k} \Vert ^{2}=0\). That is,
By the definition of \((b_{k})\) and (C1), we have
Consider the following triangular inequality:
Since \(x_{k+1} \in C_{k+1}\), therefore, we have
Utilizing (15) and (C1), the above estimate implies that
From (15), (18), and the following triangular inequality
we get
Consider the following re-arranged variant of the estimate (12) by applying Lemma 3.3:
Letting \(k \rightarrow \infty \), using (C1) and (19), we have
This implies that
Again, consider the following re-arranged variant of the estimate (13):
Letting \(k \rightarrow \infty \) and utilizing (C1), (C2), and (19), we have
This implies that
Utilizing (16), (21), (23), and the following triangle inequalities, we have
-
(i)
\(\Vert \bar{v_{k}}-b_{k}\Vert \leq \Vert \bar{v_{k}}-\bar{u_{k}} \Vert +\Vert \bar{u_{k}}-b_{k}\Vert \rightarrow 0\);
-
(ii)
\(\Vert \bar{v_{k}}-x_{k}\Vert \leq \Vert \bar{v_{k}}-b_{k}\Vert + \Vert b_{k}-x_{k}\Vert \rightarrow 0\);
-
(iii)
\(\Vert \bar{w_{k}}-b_{k}\Vert \leq \Vert \bar{w_{k}}-\bar{v_{k}} \Vert +\Vert \bar{v_{k}}-b_{k}\Vert \rightarrow 0\);
-
(iv)
\(\Vert \bar{w_{k}}-x_{k}\Vert \leq \Vert \bar{w_{k}}-b_{k}\Vert + \Vert b_{k}-x_{k}\Vert \rightarrow 0\).
From (10), (11), and Lemma 2.2, we have
Rearranging the above estimate, we have
By using (C1), (C3), (19), and \(\delta \in (0,\frac{2}{\Vert \hbar \Vert ^{2}})\), estimate (25) implies that
Note that \(J^{A_{1}}_{m_{k}}\) is firmly nonexpansive, it follows that
Utilizing (10) and (11), the expression \(J^{A_{1}}_{m_{k}}(\bar{w}_{k}+\delta \hbar ^{\ast }(J^{A_{2}}_{n_{k}}-\mathrm{Id}) \hbar \bar{w}_{k})\) from the above estimate simplifies as follows:
Setting \(\xi _{k}=J^{A_{1}}_{m_{k}}(\bar{w}_{k}+\delta \hbar ^{\ast }(J^{A_{2}}_{n_{k}}-\mathrm{Id}) \hbar \bar{w}_{k})\) in (27), it follows that
This implies that
So, we have
After simplification, we have
Making use of (19), (26), and (C3), we have the following estimate:
This implies that
Reasoning as above, we get from the definition of \((b_{k})\), (C1), and (34), that
Since \((x_{k})\) is bounded, then there exists a subsequence \((x_{k_{t}})\) of \((x_{k})\) such that \(x_{k_{t}} \rightharpoonup \bar{x_{*}} \in \mathcal{H}_{1}\) as \(t \rightarrow \infty \). Therefore \(\xi _{k_{t}}\rightharpoonup \bar{x_{*}}\) and \(\bar{w}_{k_{t}} \rightharpoonup \bar{x_{*}}\) as \(t \rightarrow \infty \). In order to show that \(\bar{x_{*}} \in \Omega \), we assume that \((r,s) \in \operatorname{gra}(A_{1})\). Since \(\xi _{k_{t}}=J^{A_{1}}_{m_{k_{t}}}(\bar{w}_{k_{t}}+\delta \hbar ^{ \ast }(J^{A_{2}}_{n_{k_{t}}}-\mathrm{Id})\hbar \bar{w}_{k_{t}})\), we have
This implies that
From the monotonicity of \(A_{1}\), we have
From the above estimate, we also have
Since \(\xi _{k_{t}} \rightharpoonup \bar{x_{*}}\), we obtain
By making use of (33), (34), and (36), it follows that
This implies that \(0 \in A_{1}(\bar{x_{*}})\). Since ħ is a bounded linear operator, we have \(\hbar \bar{w}_{k_{t}} \rightharpoonup \hbar \bar{x_{*}}\) as \(t \rightarrow \infty \). Moreover, from (26) it then follows from the demiclosedness principle that \(0 \in A_{2}(\bar{x_{*}})\), and hence \(\bar{x_{*}} \in \Omega \).
Step 4. We show that \(\bar{x_{*}} \in \bigcap^{M}_{i=1}EP(g_{i})\).
Observe that the following relation
implies via Lemma 2.4 that
This infers the existence of \(\bar{x_{*}} \in \partial _{2} g_{i}(b_{k},u^{i}_{k})\) and \(\bar{p} \in N_{C}(u^{i}_{k})\) such that
Since \(\bar{p} \in N_{C}(u^{i}_{k})\) and \(\langle \bar{p},u-u^{i}_{k} \rangle \leq 0\) for all \(u \in C\), by using (37), we have
Since \(\bar{x_{*}} \in \partial _{2}g_{i}(b_{k},u^{i}_{k})\),
Utilizing (38) and (39), we obtain
Since \(b_{k} \rightharpoonup \bar{x_{*}}\) and \(\Vert b_{k}-u^{i}_{k}\Vert \rightarrow 0\) as \(k \rightarrow \infty \), this implies \(u^{i}_{k} \rightharpoonup \bar{x_{*}}\). By using (A3) and (40), letting \(k \rightarrow \infty \), we deduce that \(g_{i}(\bar{x_{*}},u) \geq 0\) for all \(u \in C\) and \(i \in \{1,2,\ldots,M\}\). Therefore, \(\bar{x_{*}} \in \bigcap^{M}_{i=1}EP(g_{i})\).
Step 5. We show that \(\bar{x_{*}}=\bigcap^{N}_{j=1}\mathrm{Fix}(T_{j})\).
Since \(x_{k_{t}} \rightharpoonup \bar{x_{*}}\) and \(\Vert \bar{v_{k}}-x_{k}\Vert \rightarrow 0\) as \(t \rightarrow \infty \), this implies \(\bar{v_{k}} \rightharpoonup \bar{x_{*}}\). Therefore, utilizing the demiclosedness principle along with estimate (22), we have \(\bar{x_{*}} \in \bigcap^{N}_{j=1}\mathrm{Fix}(T_{j})\). Hence \(\bar{x_{*}} \in \Gamma \).
Step 6. We show that \(x_{k}\rightarrow \bar{x}=P_{\Gamma }x_{1}\).
Note that \(\bar{x}=P_{\Gamma }x_{1}\) and \(\bar{x_{*}} \in \Gamma \) implies that \(x_{k+1}=P_{\Gamma }x_{1}\) and \(\bar{x} \in \Gamma \in C_{k+1}\). This infers that \(\Vert x_{k+1}-x_{1} \Vert \leq \Vert \bar{x}-x_{1} \Vert \). On the other hand, we have
That is,
Therefore, we conclude that \(\lim_{k\rightarrow \infty }x_{k}=\bar{x_{*}}=P_{\Gamma }x_{1}\). This completes the proof. □
If we take \(A_{2}=0\) in hypothesis (H1), then we have the following results.
Corollary 3.4
Assume that \(\Gamma:= \{x \in A^{-1}_{1}(0) \cap (\bigcap^{M}_{i=1}EP(g_{i}) ) \cap (\bigcap^{N}_{j=1}\mathrm{Fix}(S_{i})\} ) \neq \emptyset \). Then the sequence \((x_{k})\) defined as
converges strongly to an element in Γ provided that conditions (C1)–(C4) hold.
4 Numerical experiment and results
This section shows the effectiveness of our algorithm by the following example and numerical results.
Example 4.1
Let \(\mathcal{H}_{1} = \mathcal{H}_{2} = \mathbb{R}\) with the inner product defined by \(\langle x, y\rangle = xy\) for all \(x, y \in \mathbb{R}\) and induced usual norm \(|\cdot |\). We define three operators \(\hbar, A_{1}, A_{2}: \mathbb{R}\rightarrow \mathbb{R}\) as \(\hbar (x)=3x\), \(A_{1}x=2x\), and \(A_{2}x=3x\) for all \(x \in \mathbb{R}\). It is clear that ħ is a bounded linear operator and \(A_{1}, A_{2}\) are maximal monotone operators such that \(\Omega:= \{\hat{x} \in A^{-1}_{1}0:\hbar \hat{x} \in A^{-1}_{2}0\}=0\). For each \(i \in \{1,2,\ldots,M\}\), let the family of pseudomonotone bifunctions \(g_{i}(x,y): C\times C \rightarrow \mathbb{R}\) on \(C = [0,1] \subset \mathbb{R}\) be defined by \(g_{i}(x,y)= T_{i}(x)(y-x)\), where
where \(0 < \mu _{1} < \mu _{2} <\cdots<\mu _{M} < 1\). Note that \(EP(g_{i})=[0,\mu _{i}]\) if and only if \(0 \leq x \leq \mu _{i}\) and \(y \in [0,1]\). Consequently, \(\bigcap^{M}_{i=1}EP(g_{i})=[0,\mu _{1}]\). For each \(j \in \{1,2,\ldots,N\}\), let the family of operators \(S_{j}: \mathbb{R} \rightarrow \mathbb{R}\) be defined by
It is also clear that \(S_{j}\) defines a finite family of \(\frac{1-j^{2}}{(1+j)^{2}}\)-demicontractive operators with \(\bigcap^{N}_{j=1}\mathrm{Fix}(S_{j})=\{0\}\). Hence \(\Gamma = \Omega \cap (\bigcap^{M}_{i=1}EP(g_{i})) \cap (\bigcap^{N}_{j=1}\mathrm{Fix}(S_{j})) = 0\). In order to compute the numerical values of \((x_{k+1})\), we choose: \(\Theta = 0.5\), \(\gamma =\frac{1}{8}\), \(\alpha _{k} =\frac{1}{100k+1}\), \(\beta _{k} =\frac{1}{100k+1}\), \(\delta =\frac{1}{9}\), \(L=3\), and \(m=0.01\). Since
Observe that the expression
in Algorithm 1 is equivalent to the following relation \(u_{k}^{i}=b_{k}-\gamma T_{i}(b_{k}) \text{ for all } i \in \{1,2, \ldots, M\}\). Similarly, \(v_{k}^{i}=b_{k}-\gamma T_{i}(u^{i}_{k}) \text{ for all } i \in \{1,2, \ldots,M\}. \) Hence, we can compute the intermediate approximation \(\bar{v}_{k}\) which is farthest from \(b_{k}\) among \(v_{k}^{i}\) for all \(i \in \{1,2,\ldots,M\}\). We compare the parallel hybrid accelerated extragradient algorithm defined in Algorithm 1 (i.e., \(\Theta _{k}\neq 0\)) and its variant with \(\Theta _{k}=0\). The stopping criteria are defined as Error=\(E_{k}=\|x_{k}-x_{k-1} \|<10^{-5}\). The values of Algorithm 1 and its variant are listed in Table 1.
The error plotting \(E_{k}\) and \((x_{k})\) of Algorithm 1 with \(\Theta _{k} \neq 0\) and \(\Theta _{k}=0\) for each choice in Table 1 is illustrated in Fig. 1.
We can see from Table 1 and Fig. 1 that Algorithm 1 performs faster and better in view of the error analysis, time consumption, and the number of iterations required for the convergence towards the desired solution in comparison with the variant of Algorithm 1 with \(\Theta _{k} = 0\).
5 Applications
In this section, we discuss some important instances of the main result in Sect. 3 as applications.
5.1 Split feasibility problems
Let \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\) be two real Hilbert spaces and \(\hbar: \mathcal{H}_{1} \rightarrow \mathcal{H}_{2}\) be a bounded linear operator. Let C and Q be nonempty, closed, and convex subsets of \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. The split feasibility problem (SFP) is the problem of finding \(\bar{x} \in C\) such that \(\hbar \bar{x} \in Q\). We represent the solution set by \(\omega:= C \cap \hbar ^{-1}(Q) = \{\bar{x} \in C: \hbar \bar{x} \in Q\}\). This problem is essentially due to Censor and Elfving [12] to solve the inverse problems and their application to medical image reconstruction, radiation therapy, and modeling and simulation in a finite dimensional Hilbert space. Recall the indicator function of C
The proximal operator of \(b_{C}\) is the metric projection on C
Let \(P_{Q}\) be the projection of \(\mathcal{H}_{2}\) onto a nonempty, closed, and convex subset Q. Take \(f(\bar{x})=\frac{1}{2}\|\hbar \bar{x}-P_{Q}\hbar \bar{x}\|^{2}\) and \(g(\bar{x})=b_{C}(\bar{x})\). Then we have the following result.
Corollary 5.1
Assume that \(\Gamma =\omega \cap (\bigcap^{M}_{i=1}EP(g_{i}) )\cap ( \bigcap^{N}_{i=1}\mathrm{Fix}(S_{j}) )\neq \emptyset \) via hypotheses (H1)–(H5). For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequence \((x_{k})\) be generated by
where \(0 < \gamma < \min (\frac{1}{2d_{1}},\frac{1}{2d_{2}})\). Assume that conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (42) converges strongly to an element in Γ.
5.2 Split variational inequality problems
Let \(A:C \rightarrow \mathcal{H}\) be a nonlinear monotone operator defined on a nonempty, closed, and convex subset C of a real Hilbert space \(\mathcal{H}\). The classical variational inequality problem aims to find a point \(\bar{x} \in C\) such that
The solution set of the above problem is denoted by \(VI(C,A)\). Let the operator \(\Pi _{A}\subset \mathcal{H} \times \mathcal{H}\) be defined by
where \(N_{C}(\bar{x}):=\{z \in \mathcal{H}:\langle \bar{y}-\bar{x}, z \rangle \leq 0 \text{ for all } \bar{y} \in C\}\). It follows from [28] that \(\Pi _{A}\) is a maximal monotone such that \(0 \in \Pi _{A}(\bar{x})\iff \bar{x} \in VI(C,A)\iff \bar{x}=P_{C}( \bar{x}-\lambda A(\bar{x}))\). As an application, we have the following result.
Corollary 5.2
Let \(\{\mathcal{H}_{n}\}_{n=1}^{2}\) be real Hilbert spaces, and let \(\{C_{n}\}_{n=1}^{2}\) be nonempty, closed, and convex subsets of \(\mathcal{H}_{n}\), respectively. Let \(A_{n}:C_{n} \rightarrow \mathcal{H}_{n}\) for \(n=1,2\) be single-valued monotone and hemicontinuous operators, and let \(\hbar:\mathcal{H}_{1} \rightarrow \mathcal{H}_{2}\) be a bounded linear operator such that \(\Gamma =VI(C_{1},A_{1})\cap \hbar ^{-1} (VI(C_{2},A_{2})) \cap ( \bigcap^{M}_{i=1}EP(g_{i}) )\cap (\bigcap^{N}_{j=1}\mathrm{Fix}(S_{j}) ) \neq \emptyset \) via hypotheses (H1)–(H5). For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequences \((x_{k})\) be generated by
where \(0 < \gamma < \min (\frac{1}{2d_{1}},\frac{1}{2d_{2}})\) and \(P_{C_{1}}^{(A_{1},\lambda )}\), \(P_{C_{2}}^{(A_{2},\lambda )}\) denote \(P_{C}(\mathrm{Id}-\lambda A)\). Assume that conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (43) converges strongly to an element in Γ.
5.3 Split optimization problems
Let \(\phi: \mathcal{H}_{1} \rightarrow (-\infty,\infty ]\) be a proper, convex, and lower semicontinuous (pcls) function, then the set of minimizers associated with ϕ is defined as
Recall that ∂ϕ of the pcls function ϕ is a maximal monotone operator and the corresponding resolvent operator of ∂ϕ is called the proximity operator (see [17]). Hence argmin \(\phi = (\partial \phi )^{-1}(0)\). Hence, we have the following application.
Corollary 5.3
Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two Hilbert spaces, and let \(C \subseteq \mathcal{H}_{1}\) be nonempty, closed, and convex subset of \(\mathcal{H}_{1}\). Let \(\phi _{1}\) and \(\phi _{2}\) be pcls functions on \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. Assume that \(\Gamma = \{x \in \arg \min \phi _{1}:\hbar x \in \arg \min \phi _{2} \} \cap (\bigcap^{M}_{i=1}EP(g_{i}))\cap (\bigcap_{i=1}^{N}\mathrm{Fix}(S_{j})) \neq \emptyset \) via hypotheses (H1)–(H5). For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequence \((x_{k})\) be generated by
where \(0 < \gamma < \min (\frac{1}{2d_{1}},\frac{1}{2d_{2}})\). Assume that conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (44) converges strongly to an element in Γ.
6 Conclusions
In this paper, we have analyzed an accelerated projection based parallel hybrid extragradient algorithm for pseudomonotone equilibrium, fixed point, and split null point problems in Hilbert spaces. The convergence analysis of the algorithm is established under the suitable set of conditions. A suitable numerical example has been incorporated to exhibit the effectiveness of the algorithm. Moreover, some well-known instances, as applications, of the main result that can pave a way for an important future research direction are also discussed.
Availability of data and materials
Data sharing not applicable to this article as no data-sets were generated or analysed during the current study.
References
Alvarez, F., Attouch, H.: An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 9, 3–11 (2001)
Anh, P.N.: A hybrid extragradient method for pseudomonotone equilibrium problems and fixed point problems. Bull. Malays. Math. Sci. Soc. 36(1), 107–116 (2013)
Arfat, Y., Kumam, P., Khan, M.A.A., Ngiamsunthorn, P.S., Kaewkhao, A.: An inertially constructed forward-backward splitting algorithm in Hilbert spaces. Adv. Differ. Equ. 2021, 124 (2021)
Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A.: An inertial based forward-backward algorithm for monotone inclusion problems and split mixed equilibrium problems in Hilbert spaces. Adv. Differ. Equ. 2020, 453 (2020)
Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A.: An accelerated projection based parallel hybrid algorithm for fixed point and split null point problems in Hilbert spaces. Math. Methods Appl. Sci. (2021). https://doi.org/10.1002/mma.7405
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operators Theory in Hilbert Spaces. CMS Books in Mathematics. Springer, New York (2011)
Blum, E., Oettli, W.: From optimization and variational inequalities to equilibrium problems. Math. Stud. 63, 123–145 (1994)
Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103–120 (2004)
Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)
Ceng, L.C.: Modified inertial subgradient extragradient algorithms for pseudomonotone equilibrium problems with the constraint of nonexpansive mappings. J. Nonlinear Var. Anal. 5, 281–297 (2021)
Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)
Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 8, 221–239 (1994)
Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59, 301–323 (2012)
Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Nonlinear Convex Anal. 16, 587–600 (2009)
Combettes, P.L.: The convex feasibility problem in image recovery. Adv. Imaging Electron Phys. 95, 155–453 (1996)
Combettes, P.L.: Solving monotone inclusions via compositions of nonexpansive averaged operators. Optimization 53, 475–504 (2004)
Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Fixed-Point Algorithms Inverse Prob. Sci. Eng., pp. 185–212 (2011)
Farid, M.: The subgradient extragradient method for solving mixed equilibrium problems and fixed point problems in Hilbert spaces. J. Appl. Numer. Optim. 1, 335–345 (2019)
Gibali, A.: A new split inverse problem and an application to least intensity feasible solutions. Pure Appl. Funct. Anal. 2, 243–258 (2017)
Hieu, D.V., Muu, L.D., Anh, P.K.: Parallel hybrid extragradient methods for pseudomonotone equilibrium problems and nonexpansive mappings. Numer. Algorithms 73, 197–217 (2016)
Khan, M.A.A.: Convergence characteristics of a shrinking projection algorithm in the sense of Mosco for split equilibrium problem and fixed point problem in Hilbert spaces. Linear Nonlinear Anal. 3, 423–435 (2017)
Khan, M.A.A., Arfat, Y., Butt, A.R.: A shrinking projection approach to solve split equilibrium problems and fixed point problems in Hilbert spaces. UPB Sci. Bull., Ser. A 80(1), 33–46 (2018)
Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Ekon. Mat. Metody 12, 747–756 (1976)
Martinez-Yanes, C., Xu, H.K.: Strong convergence of CQ method for fixed point iteration processes. Nonlinear Anal. 64, 2400–2411 (2006)
Moudafi, A., Oliny, M.: Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 155, 447–454 (2003)
Polyak, B.T.: Introduction to Optimization, Optimization Software. New York (1987)
Quoc, T.D., Muu, L.D., Hien, N.V.: Extragradient algorithms extended to equilibrium problems. Optimization 57, 749–776 (2008)
Rockafellar, R.T.: On the maximality of sums of nonlinear monotone operators. Trans. Am. Math. Soc. 149, 75–88 (1970)
Tada, A., Takahashi, W.: Strong Convergence Theorem for an Equilibrium Problem and a Nonexpansive Mapping. Nonlinear Anal. Conv. Anal. Yokohama Publishers, Yokohama (2006)
Takahashi, W., Xu, H.K., Yao, J.C.: Iterative methods for generalized split feasibility problems in Hilbert spaces. Set-Valued Var. Anal. 23, 205–221 (2015)
Tiel, J.: Convex Analysis. An Introductory Text. Wiley, Chichester (1984)
Yen, L.H., Muu, L.D.: A normal-subgradient algorithm for fixed point problems and quasiconvex equilibrium problems. Appl. Set-Valued Anal. Optim. 2(3), 329–337 (2020)
Acknowledgements
The authors wish to thank the anonymous referees for their comments and suggestions. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. This research was supported by Research Center in Mathematics and Applied Mathematics, Chiang Mai University. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005.
Funding
This research was supported by Chiang Mai University. The author Yasir Arfat was supported by the Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi, Thailand (Grant No.16/2562).
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arfat, Y., Kumam, P., Khan, M.A.A. et al. A parallel hybrid accelerated extragradient algorithm for pseudomonotone equilibrium, fixed point, and split null point problems. Adv Differ Equ 2021, 364 (2021). https://doi.org/10.1186/s13662-021-03518-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03518-2
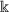 -demicontractive operators;
-demicontractive operators; ;
;
