- Research
- Open access
- Published:
Application of some special operators on the analysis of a new generalized fractional Navier problem in the context of q-calculus
Advances in Difference Equations volume 2021, Article number: 402 (2021)
Abstract
The key objective of this study is determining several existence criteria for the sequential generalized fractional models of an elastic beam, fourth-order Navier equation in the context of quantum calculus (q-calculus). The required way to accomplish the desired goal is that we first explore an integral equation of fractional order w.r.t. q-RL-integrals. Then, for the existence of solutions, we utilize some fixed point and endpoint conditions with the aid of some new special operators belonging to operator subclasses, orbital α-admissible and α-ψ-contractive operators and multivalued operators involving approximate endpoint criteria, which are constructed by using aforementioned integral equation. Furthermore, we design two examples to numerically analyze our results.
1 Introduction
With the passing of years and even decades, people need to be more and more aware of details of various natural phenomena. The logical tools and notions available in mathematics and especially mathematical operators are one of possible ways to achieve this aim in modeling various processes. In this direction, many researchers developed numerous fractional operators such that their applicability and usefulness become more and more evident to researchers each day. As a result, using fractional operators, different processes are modeled and examined from all aspects in the mathematical structures such as boundary value problems. In broad fields such as chemistry, biology, physics, economics, engineering, and so on fractional calculus, related differential equations and BVPs are commonly used [1–5]. In a vast domain of papers, scientists have examined numerous mathematical procedures across different facets of fractional differential equations [6–13].
In recent years, there has been a great deal of interest in the analysis of q-difference equations. These equations have been found to be applicable in various fields of physics and mechanics and thus have been developed into multidisciplinary topics. Fractional q-calculus is considered as a special fractional variant of calculus, originally it was suggested by Jackson [14]. and then further investigations were performed by Al-Salam and Agarwal [15, 16]. Some fascinating studies into IVPs and BVPs with equations involving q-operators are available in [17–31].
More specifically, Ferreira [32] considered the following nonlinear fractional terminal q-BVP and discussed the existence of a nontrivial solution:
where \(\mathfrak{t}\in \mathcal{O}=[0, 1]\), \(\mathfrak{D}_{q}^{\ell _{1}}\) is the standard Riemann–Liouville fractional q-derivative, and \(M:\mathcal{O}\times \mathbb{R}\to \mathbb{R}\) is a continuous function.
Ahmad and Ntouyas [33] in 2011 studied the following q-analogue of second-order q-difference inclusion BVP and investigated the existence criteria using results from fixed point theory:
where \(\mathfrak{t}\in [0, {T}]\), \(\alpha \in \mathbb{R}\setminus \{1\}\), and \(\mathfrak{M}: [0, {T}]\times \mathbb{R}\to \mathbb{P}( \mathbb{R})\) a compact-valued map.
Ahmad et al. [17] studied the existence criteria for the q-difference inclusion involving q-antiperiodic conditions
where \(\mathfrak{t}\in \mathcal{O}\), \(q\in (0, 1)\), \(2< \ell _{1} \leq 3\), \({^{C}\mathfrak{D}}_{q}^{\ell _{1}}\) denotes the q-fractional derivative in the Caputo sense of order \(\ell _{1}\), and \(\mathfrak{M}: \mathcal{O}\times \mathbb{R}^{3}\to \mathbb{P}( \mathbb{R})\) involves some specifications.
An elastic beam is considered as an essential feature in constructions like ships, bridges, building structures, and aviation industry. In this direction and in mathematical point of view, the following fourth-order BVP of Navier differential equation can be used in modeling deformation of the beam (see [34]):
where \(M: \mathcal{O}\times \mathbb{R}^{2}\to \mathbb{R}\) is continuous, and \(\mathfrak{t} \in \mathcal{O} := [0,1]\). By transforming (1) into the second-order integro–differential equation with bounded M, Aftabizadeh [35] utilized Schauder’s fixed-point theorem and discussed the existence and uniqueness of solutions for (1). The upper and lower solution method was used by Ma et al. [36] for problem (1). In 2004, Bai et al. [37] extended a monotone method to upper and lower solutions of the beam model (1). In the context of fractional calculus, Bachar and Eltayeb [38] proposed the fractional variant of the Riemann–Liouville model (1) and explored the existence, uniqueness, and positivity for the solutions of a system designed by the following format:
where \(\ell _{1} \in (1,2]\), \(\ell _{2} \in (1,2)\), \({}^{RL}\mathfrak{D}^{\ell _{1} }\) and \({}^{RL}\mathfrak{D}^{\ell _{2} }\) are the fractional derivatives in the Riemann–Liouville sense, and \(M: \mathcal{O}\times \mathbb{R}^{2}\to \mathbb{R}\) is continuous. In the case \(\ell _{1} =\ell _{2}=2\), problem (2) reduces to (1).
Inspired by aforesaid ideas given in the papers mentioned, in terms of the standard Navier equation, we review and discuss a new sequential generalized fractional q-Navier BVP
along with its inclusion version given by
where \(\ell _{1} \in (1,2]\), \(\ell _{2} \in (1,2)\), and \(\gamma , \delta , \lambda , \beta \in \mathbb{R}^{+}\). Moreover, the operator \({}^{C}\mathfrak{D}_{q}^{(\cdot )}\) is the q-derivative of given fractional orders in the Caputo sense. Furthermore, a continuous single-valued function \(M : \mathcal{O} \times \mathbb{R}^{2} \to \mathbb{R}\) and a multivalued function \(\mathfrak{M} : \mathcal{O} \times \mathbb{R}^{2} \to \mathbb{P}( \mathbb{R})\) are assumed to be arbitrary equipped with some required specifications explained subsequently.
The novelty of our paper is that the above suggested structure for Navier problem is unique and novel, which can be regarded as a generalized fractional model of the standard Navier problem in the context of quantum operators. Indeed, by taking \(\ell _{1} = \ell _{2} = 2\), \(q\to 1\), and \(\gamma = \delta = \lambda = \beta = 1\) we have the standard Navier BVP (1). Also, we establish our results by new techniques involving some special operators.
We have organized the remaining sections of the paper as follows. The upcoming section is assigned to the basic ideas of fractional q-calculus. Section 3 starts with a lemma, which specifies the solution of our proposed Navier BVPs (3)–(4) in terms of an integral equation of noninteger order. After that, we follow the well.-known fixed-point methods due to Krasnoselskii [39] and new operators introduced by Samet et al. [40] to obtain the existence of solutions for single-valued maps. In Sect. 4, we consider the inclusion variant (4) of the Navier BVP and explore the existence of solutions using the methods presented by Mohammadi et al. [41] and approximated end-point property. Section 5 provides illustrations of the results given in Sects. 3 and 4. In the last section, we present the concluding remarks and future proposals.
2 Basic preliminaries
We assemble and examine supplementary and fundamental concepts concerning q-calculus in the light of our approaches to this research.
We suppose that \(0< q<1\). A q-analogue of the function \((m_{1} - m_{2})^{n}\) given for \(n\in \mathbb{N}_{0}\) is defined by \((m_{1} - m_{2})^{(0)} = 1\) and
where \(m_{1}, m_{2} \in \mathbb{R}\) and \(\mathbb{N}_{0} := \{ 0,1,2, \dots \}\) [42]. Let now \(n = \omega \) be a constant in \(\mathbb{R}\). Let us now define the following q-analogue of the existing power mapping \((m_{1} - m_{2})^{n}\) in a q-fractional setting:
for \(m_{1}\neq 0\). Note that by taking \(m_{2}=0\) we immediately obtain the equality \(m_{1}^{(\omega )}=m_{1}^{\omega } \) [42]. For a real number \(m_{1} \in \mathbb{R} \), a q-number \([ m_{1} ]_{q} \) is expressed as
The q-gamma function is defined as
for \(\varsigma \in \mathbb{R} \setminus \{ 0, -1, -2, \ldots \} \) [42, 43]. Note that \(\Gamma _{q}(\varsigma +1)=[\varsigma ]_{q} \Gamma _{q} (\varsigma )\) [43].
For a real-valued continuous function μ, the quantum derivative of this function is defined as
and also \((\mathfrak{D}_{q} \mu )(0) = \lim_{\mathfrak{t}\to 0}(\mathfrak{D}_{q} \mu )(\mathfrak{t})\) [44]. Given a function μ, its quantum derivative can be extended to an arbitrary higher order by \((\mathfrak{D}_{q}^{n} \mu )(\mathfrak{t}) = \mathfrak{D}_{q} ( \mathfrak{D}_{q}^{n -1} \mu )(\mathfrak{t})\) for any \(n \in \mathbb{N}\) [44]. Obviously, \((\mathfrak{D}_{q}^{0} \mu )(\mathfrak{t}) = \mu (\mathfrak{t})\).
Given a continuous map \(\mu : [0,c_{2}] \to \mathbb{R}\), the quantum integral of this function can be defined by
provided that the absolute convergence of the series holds [44]. The quantum integral of μ can be similarly extended like the quantum derivative to an arbitrary higher order using the iterative rule \((\mathfrak{I}_{q}^{n} \mu )(\mathfrak{t}) = \mathfrak{I}_{q}( \mathfrak{I}_{q}^{ n -1}\mu )(\mathfrak{t})\) for \(n \geq 1\) [44].
If a function μ is continuous at \(\mathfrak{t}=0\), then \((\mathfrak{I}_{q} \mathfrak{D}_{q} \mu )(\mathfrak{t})= \mu ( \mathfrak{t})- \mu (0)\) [44]. Moreover, \((\mathfrak{D}_{q} \mathfrak{I}_{q} \mu )(\mathfrak{t})= \mu ( \mathfrak{t})\) for all \(\mathfrak{t}\). In this case, by considering a real number \(\ell \geq 0\) such that \(n-1 < \ell <n\), that is, \(n = [ \ell ]+1 \), for a function \(\mu \in \mathcal{C}_{\mathbb{R}}([0,+ \infty ))\), the Riemann–Liouville quantum integral is defined as
provided that the above value is finite and \({}^{R}\mathfrak{I}_{q}^{ 0 } \mu (\mathfrak{t}) = \mu (\mathfrak{t})\) [32, 45]. Further, the semigroup specification for the mentioned q-operator occurs such that \({}^{R}\mathfrak{I}_{q}^{\ell _{1}} ({}^{R}\mathfrak{I}_{q}^{\ell _{2}} \mu )(\mathfrak{t})= {}^{R}\mathfrak{I}_{q}^{\ell _{1} + \ell _{2}} \mu (\mathfrak{t})\) for \(\ell _{1} , \ell _{2} \geq 0 \) [32]. For \(\varsigma \in (-1, \infty )\), we have the following property:
It is evident that if \(\varsigma = 0\), then \({}^{R}\mathfrak{I}_{q}^{\ell }1(\mathfrak{t})= \frac{1}{\Gamma _{q}(\ell +1)} \mathfrak{t}^{\ell }\) for any \(\mathfrak{t}>0\). Given a function \(\mu \in \mathcal{C}^{(n)}_{\mathbb{R}}([0,+ \infty ))\), its Caputo q-derivative is defined as
if the integral exists [32, 45]. We have the following property:
It is evident that \({}^{C}\mathfrak{D}_{q}^{\ell }1(\mathfrak{t})= 0 \) for any \(\mathfrak{t}>0\).
Lemma 2.1
([46])
Let \(n-1 < \ell < n \). Then
According to this lemma, the fractional quantum differential equation \({}^{C}\mathfrak{D}_{q}^{ \ell }\mu (\mathfrak{t}) =0\) has a general solution \(\mu (\mathfrak{t}) = \mathfrak{m}_{0} + \mathfrak{m}_{1} \mathfrak{t} + \mathfrak{m}_{2} \mathfrak{t}^{2} + \cdots + \mathfrak{m}_{n-1} \mathfrak{t}^{n-1}\), where \(\mathfrak{m}_{0}, \dots , \mathfrak{m}_{n-1}\in \mathbb{R}\) and \(n = [ \ell ] + 1\) [46]. It is worth noting that for each continuous μ, according to Lemma 2.1, we get
where \(\mathfrak{m}_{0}, \dots , \mathfrak{m}_{n-1}\) are constants contained in \(\mathbb{R}\), and \(n = [ \ell ]+1\) [46].
Notation 2.2
Let \((\mathfrak{A}_{*}, \Vert \cdot \Vert _{\mathfrak{A}_{*} })\) be a normed space. By \(\mathbb{P}_{\mathbb{B}}(\mathfrak{A}_{*})\), \(\mathbb{P}_{\mathbb{CL}}( \mathfrak{A}_{*})\), \(\mathbb{P}_{\mathbb{CM}}(\mathfrak{A}_{*})\), and \(\mathbb{P}_{\mathbb{CX}}(\mathfrak{A}_{*})\) we denote the classes of all bounded, closed, compact, and convex sets in \(\mathfrak{A}_{*}\), respectively.
Let Ψ be the subclass of nondecreasing operators \(\psi : [0, \infty ) \to [0, \infty )\) such that
For more information about the following definitions, see [47–51].
Definition 2.3
([40])
Let \(M: \mathfrak{A}_{*}\to \mathfrak{A}_{*}\) and \(\alpha : \mathfrak{A}_{*}^{2} \to \mathbb{R}_{\geq 0}\). Then
-
(i)
M is an α-ψ-contraction if for \(\mu _{1}, \mu _{2}\in \mathfrak{A}_{*}\),
$$ \alpha (\mu _{1},\mu _{2}) d(M \mu _{1}, M \mu _{2})\leq \psi \bigl(d(\mu _{1}, \mu _{2})\bigr). $$ -
(ii)
M is α-admissible if \(\alpha (\mu _{1},\mu _{2}) \geq 1\) yields \(\alpha (M\mu _{1},M\mu _{2}) \geq 1\).
Definition 2.4
([52])
-
(1)
A member \(\mu \in \mathfrak{A}_{*}\) is called an end-point of a multivalued function \(\mathfrak{M}:\mathfrak{A}_{*} \rightarrow \mathbb{P}(\mathfrak{A}_{*})\) if \(\mathfrak{M}(\mu )=\{\mu \}\).
-
(2)
A multivalued map \(\mathfrak{M}\) admits an approximate end-point criterion (AEP) if
$$ \inf_{\mu _{1} \in \mathfrak{A}_{*}} \Bigl[ \sup_{\mu _{2} \in \mathfrak{M}(\mu _{1})} d(\mu _{1},\mu _{2}) \Bigr] = 0. $$
Definition 2.5
([41])
Let \(\mathfrak{M} :\mathfrak{A}_{\star }\to \mathbb{P}_{\mathbb{CL,B}}( \mathfrak{A}_{\star })\), \(\alpha : \mathfrak{A}_{\star }^{2} \to [0, +\infty )\), and \(\psi \in \Psi \). Then
-
(1)
\(\mathfrak{M}\) is orbital α-admissible if for all \(\mu _{1} \in \mathfrak{A}_{\star }\) and \(\mu _{2}\in \mathfrak{M}\mu _{1}\), the inequality \(\alpha (\mu _{1},\mu _{2})\geq 1\) implies \(\alpha (\mu _{2},\mu _{3})\geq 1\) for each \(\mu _{3}\in \mathfrak{M}\mu _{2}\).
-
(2)
\(\mathfrak{M}\) is an α-ψ-contractive multi–function if for all \(\mu _{1}, \mu _{2}\in \mathfrak{A}_{\star }\),
$$ \alpha (\mu _{1},\mu _{2}) \mathbb{H}_{d} ( \mathfrak{M} \mu _{1}, \mathfrak{M} \mu _{2})\leq \psi \bigl(d(\mu _{1},\mu _{2})\bigr), $$where \(\mathbb{H}_{d}\) is the Pompeiu–Hausdorff metric.
We recall some necessary fixed-point results in connection with the suggested boundary problem.
Theorem 2.6
([40])
Let \((\mathfrak{A}_{*}, \mathrm{d})\) be a complete metric space, let \(\alpha : \mathfrak{A}_{*} \times \mathfrak{A}_{*} \to \mathbb{R}\) and \(\psi \in \Psi \), and let \(M:\mathfrak{A}_{*} \to \mathfrak{A}_{*}\) be an α-ψ-contractive map such that:
-
(1)
M is α-admissible self-map on \(\mathfrak{A}_{*}\);
-
(2)
for some \(\mu _{0} \in \mathfrak{A}_{*}\), \(\alpha (\mu _{0},M\mu _{0}) \geq 1\);
-
(3)
for any sequence \(\{\mu _{n}\}\) in \(\mathfrak{A}_{*}\) such that \(\mu _{n} \to \mu \) and \(\alpha (\mu _{n}, \mu _{n+1}) \geq 1\) for all \(n \geq 1\), we have \(\alpha (\mu _{n}, \mu ) \geq 1\) for all \(n \geq 1\).
Then there is a fixed–point for M.
Theorem 2.7
([39], Krasnoselskii)
Let \(G \neq \emptyset \) be a closed bounded convex set contained in a Banach space \(\mathfrak{A}_{*}\), and let \(M_{1}\) and \(M_{2}\) be such that:
-
(1)
\(M_{1}\mu _{1} + M_{2}\mu _{2} \in G\) for \(\mu _{1}, \mu _{2} \in G\);
-
(2)
\(M_{1}\) is compact and continuous;
-
(3)
\(M_{2}\) is a contraction.
Then there exists \(\mu \in G\) such that \(\mu = M_{1}\mu + M_{2}\mu \).
Theorem 2.8
([41])
Let \((\mathfrak{A}_{*}, \mathrm{d})\) be a complete metric space, let \(\alpha : \mathfrak{A}_{*} \times \mathfrak{A_{*}} \to [0, \infty )\), and let \(\psi \in \Psi \) be a strictly increasing map. Moreover, let \(\mathfrak{M}:\mathfrak{A}_{*} \to \mathbb{P}_{\mathbb{CL,\mathbb{B}}}( \mathfrak{A}_{*})\) be an α-ψ-contraction, Assume that:
-
1
\(\mathfrak{M}\) is orbital α-admissible;
-
2
\(\alpha (\mu _{0},\mu _{1}) \geq 1\) for some \(\mu _{0} \in \mathfrak{A_{*}}\) and \(\mu _{1} \in \mathfrak{M}\mu _{0}\);
-
3
the space \(\mathfrak{A}_{*}\) has the property that for each sequence \(\{\mu _{n}\}\) in \(\mathfrak{A}_{*}\) such that \(\alpha (\mu _{n}, \mu _{n+1}) \geq 1\) and \(\mu _{n} \to \mu \) for all \(n \in \mathbb{N}\), there exists a subsequence \(\{ \mu _{n_{r}} \}\) of \(\{ \mu _{n} \}\) such that \(\alpha (\mu _{n_{r}}, \mu ) \geq 1\) for all \(r \in \mathbb{N}\).
Then \(\mathfrak{M}\) has a fixed point.
Theorem 2.9
([52])
Let \((\mathfrak{A}_{*}, \mathrm{d})\) be a complete metric space. In addition, consider:
-
1
a map \(\psi : [0, \infty ) \to [0, \infty )\) which is u.s.c with \(\psi (\mathfrak{t}) < \mathfrak{t}\) and \(\liminf_{\mathfrak{t} \to \infty }(\mathfrak{t} - \psi (\mathfrak{t})) >0\) for all \(\mathfrak{t} >0\),
-
2
a multivalued map \(\mathfrak{M}: \mathfrak{A}_{*} \to \mathbb{P}_{ \mathbb{CL,\mathbb{B}}}(\mathfrak{A}_{*})\) such that \(\mathbb{H}_{\mathrm{d}}(\mathfrak{M} \mu _{1}, \mathfrak{M} \mu _{2}) \leq \psi (d(\mu _{1}, \mu _{2}))\) for any \(\mu _{1}, \mu _{2} \in \mathfrak{A}_{*}\).
Then a unique endpoint of \(\mathfrak{M}\) exists iff \(\mathfrak{M}\) has an approximate end-point criterion.
3 Results for q-Navier FBVP (3)
Consider the space \(\mathfrak{A}_{*} = \{ \mu (\mathfrak{t}): \mu (\mathfrak{t}),{}^{C} \mathfrak{D}_{q}^{\ell _{2} } \mu (\mathfrak{t}) \in \mathcal{C}_{ \mathbb{R}}(\mathcal{O}) \}\) of all continuous functions on \(\mathcal{O}\) along with real values, which is a Banach space under the sup norm \(\Vert \mu \Vert _{\mathfrak{A}_{*}} =\sup_{\mathfrak{t}\in \mathcal{O}} \vert \mu (\mathfrak{t}) \vert + \sup_{\mathfrak{t}\in \mathcal{O}} \vert {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\mu ( \mathfrak{t}) \vert \) for \(\mu \in \mathfrak{A}_{*}\). The following lemma presents a solution to the proposed problem (3) in the form of an integral equation, which is important in determining our key findings.
Lemma 3.1
Let \(\eta \in \mathfrak{A}_{*}\), \(\ell _{1} , \ell _{2} \in (1,2)\), and \(\gamma , \delta , \lambda , \beta \in \mathbb{R}^{+}\). Then \(\mu ^{*}\) is a solution to the nonlinear sequential fractional q-Navier BVP
if and only if it satisfies the q-integral equation
Proof
First, let a function \(\mu ^{*}\) be a solution of the nonlinear sequential generalized q-Navier FBVP (9). Then \({}^{C}\mathfrak{D}_{q}^{\ell _{1} } ( {}^{C}\mathfrak{D}_{q}^{ \ell _{2} } \mu ^{*} ) (\mathfrak{t}) = \eta (\mathfrak{t})\). Since \(\ell _{1} \in (1,2)\), taking the \(\ell _{1}^{\mathrm{th}}\)-q-integral in the Riemann–Liouville setting, we obtain
where we need to find the constants \(\mathfrak{m}_{0}, \mathfrak{m}_{1} \in \mathbb{R}\). By the third condition \(\lambda {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\mu (0) = 0\) we obtain \(\mathfrak{m}_{0} = 0\). So
On the other hand, by (11) and the fourth condition \(\beta {}^{C}\mathfrak{D}_{q}^{\ell _{2} } \mu (1) = 0\) we get
and thus
In view of (12), relation (11) becomes
Again, since \(\ell _{2} \in (1,2)\), taking the \(\ell _{2}^{\mathrm{th}}\)-q-integral in the Riemann–Liouville setting in (13), we obtain
where the constants \(\mathfrak{m}^{*}_{0}, \mathfrak{m}^{*}_{1} \in \mathbb{R}\) are to find. The first condition \(\gamma \mu (0)= 0\) gives \(\mathfrak{m}_{0}^{*} = 0\). In consequence,
At last, the second condition \(\delta \mu (1)= 0\) implies that
Consequently,
Inserting \(\mathfrak{m}_{1}^{*}\) into (14), we obtain
which yields that \(\mu ^{*}\) settles q-integral equation (10). On the other hand, we can simply prove the converse by direct computation, and ultimately the arguments are finished. □
Now consider the operator \(\mathfrak{N}:\mathfrak{A}_{*} \to \mathfrak{A}_{*}\) defined by
We can easily infer that \(\mu ^{*}\) is a solution of fractional q-Navier BVP (3) iff \(\mu ^{*}\) is a fixed point of the operator \(\mathfrak{N}\). For simplicity, set
and
Theorem 3.2
Suppose there exist a map \(\mathfrak{U}:\mathbb{R}^{2} \times \mathbb{R}^{2} \rightarrow \mathbb{R}\), a continuous function \(M: \mathcal{O} \times \mathfrak{A}^{2}_{*} \to \mathfrak{A}_{*}\), and a nondecreasing function \(\psi \in \Psi \) such that:
- \((\mathfrak{X}_{1})\):
-
for any \(\mu _{1}, \mu _{2}, w_{1}, w_{2} \in \mathfrak{A}_{*}\) and \(\mathfrak{t} \in \mathcal{O}\), we have
$$ \bigl\vert M(\mathfrak{t}, \mu _{1}, w_{1}) - M( \mathfrak{t}, \mu _{2}, w_{2}) \bigr\vert \leq \tilde{ \mathfrak{x}} \psi \bigl( \vert \mu _{1}-\mu _{2} \vert + \vert w_{1}-w_{2} \vert \bigr){} $$with
$$ \mathfrak{U} \bigl( \bigl(\mu _{1}(\mathfrak{t}), w_{1}( \mathfrak{t}) \bigr), \bigl(\mu _{2}(\mathfrak{t}), w_{2}( \mathfrak{t}) \bigr) \bigr) \geq 0, $$where \(\tilde{\mathfrak{x}}= \frac{1}{\Lambda _{1}^{\star }+\Lambda _{2}^{\star }}\);
- \((\mathfrak{X}_{2})\):
-
there exists \(\mu _{0} \in \mathfrak{A}_{*}\) such that for all \(\mathfrak{t} \in \mathcal{O}\),
$$ \mathfrak{U} \bigl( \bigl(\mu _{0}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} } \mu _{0}(\mathfrak{t}) \bigr), \bigl(\mathfrak{N}\mu _{0}( \mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} } \bigl( \mathfrak{N} \mu _{0}( \mathfrak{t}) \bigr) \bigr) \bigr) \geq 0{} $$and
$$ \mathfrak{U} \bigl( \bigl(\mu _{1}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} } \mu _{1}(\mathfrak{t}) \bigr), \bigl(\mu _{2}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu _{2}(\mathfrak{t}) \bigr) \bigr) \geq 0, $$which gives
$$ \mathfrak{U} \bigl( \bigl(\mathfrak{N}\mu _{1}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} } \bigl(\mathfrak{N} \mu _{1}(\mathfrak{t}) \bigr) \bigr), \bigl(\mathfrak{N}\mu _{2}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2}} \bigl(\mathfrak{N}\mu _{2}(\mathfrak{t}) \bigr) \bigr) \bigr) \geq 0{} $$for all \(\mu _{1},\mu _{2} \in \mathfrak{A}_{*}\) and \(\mathfrak{t} \in \mathcal{O}\);
- \((\mathfrak{X}_{3})\):
-
for any convergent sequence \(\{\mu _{n} \}_{n\geq 1}\) in \(\mathfrak{A}_{*}\) such that \(\mu _{n} \to \mu \) and
$$ \mathfrak{U} \bigl( \bigl(\mu _{n}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} } \mu _{n}(\mathfrak{t}) \bigr), \bigl(\mu _{n+1}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu _{n+1}(\mathfrak{t}) \bigr) \bigr) \geq 0{} $$for all n and \(\mathfrak{t} \in \mathcal{O}\), we have
$$ \mathfrak{U} \bigl( \bigl(\mu _{n}(\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} } \mu _{n}(\mathfrak{t}) \bigr), \bigl(\mu (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} } \mu (\mathfrak{t}) \bigr) \bigr) \geq 0. $$
Then the generalized q-Navier BVP (3) has a solution.
Proof
Let \(\mu _{1}\) and \(\mu _{2}\) belong to \(\mathfrak{A}_{*}\) with
for each \(\mathfrak{t} \in \mathcal{O}\). Then we may write
and, similarly, we get
Consequently, we have
Now let \(\alpha :\mathfrak{A}_{*} \times \mathfrak{A}_{*} \to [0, \infty )\) be the function defined as
for any \(\mu _{1},\mu _{2} \in \mathfrak{A}_{*}\). Then we get \(\alpha (\mu _{1},\mu _{2})\mathrm{d}(\mathfrak{N}\mu _{1}, \mathfrak{N}\mu _{2}) \leq \psi (\mathrm{d}(\mu _{1},\mu _{2}))\) for all \(\mu _{1},\mu _{2} \in \mathfrak{A}_{*}\). Thus \(\mathfrak{N}\) is an α-ψ-contraction. It is also simple to verify that \(\mathfrak{N}\) is α-admissible and \(\alpha (\mu _{0}, \mathfrak{N} \mu _{0}) \geq 1\). On the other hand, let \(\{\mu _{n}\}_{n\geq 1}\) be a sequence in \(\mathfrak{A}_{*}\) such that \(\mu _{n} \to \mu \) and \(\alpha (\mu _{n}, \mu _{n+1}) \geq 1\) for all n. By the definition of the nonnegative function α we have
Therefore by the hypothesis we obtain
This indicates that \(\alpha (\mu _{n},\mu ) \geq 1\) for every n. Ultimately, by Theorem 2.6 we conclude that \(\mathfrak{N}\) has a fixed point \(\mu ^{**} \in \mathfrak{A}_{*}\). This implies that \(\mu ^{**}\) is a solution of the generalized q-Navier FBVP (3), and the proof is completed. □
Theorem 3.3
Let \(M:\mathcal{O} \times \mathfrak{A}_{*}^{2} \to \mathfrak{A}_{*}\) be a continuous function. Assume the following conditions:
- \((\mathfrak{X}_{4})\):
-
there is
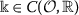 such that for all \(\mathfrak{t} \in \mathcal{O}\) and \(\mu _{1},\mu _{2},w_{1},w_{2} \in \mathfrak{A}_{*}\),
such that for all \(\mathfrak{t} \in \mathcal{O}\) and \(\mu _{1},\mu _{2},w_{1},w_{2} \in \mathfrak{A}_{*}\), 
- \((\mathfrak{X}_{5})\):
-
there exist a continuous function \(\varrho :\mathcal{O} \to \mathbb{R}^{+}\) and a continuous nondecreasing function \(\psi :\mathbb{R}^{+} \to \mathbb{R}^{+}\) such that for all \(\mathfrak{t} \in \mathcal{O}\) and \(\mu _{1},\mu _{2} \in \mathfrak{A}_{*}\),
$$ \bigl\vert M(\mathfrak{t},\mu _{1},\mu _{2}) \bigr\vert \leq \varrho ( \mathfrak{t}) \psi \bigl( \vert \mu _{1} \vert + \vert \mu _{2} \vert \bigr). $$
Then if

where  and \(\Xi _{1}^{\star }\), \(\Xi _{2}^{\star }\) are defined in (16), then the generalized q-Navier FBVP (3) has a solution.
and \(\Xi _{1}^{\star }\), \(\Xi _{2}^{\star }\) are defined in (16), then the generalized q-Navier FBVP (3) has a solution.
Proof
Define \(\Vert \varrho \Vert = \sup_{\mathfrak{t} \in \mathcal{O}} \vert \varrho (\mathfrak{t}) \vert \) and choose an appropriate constant \(\varepsilon >0\) such that
where \(\Lambda _{1}^{\star }\) and \(\Lambda _{2}^{\star }\) are defined in (15). Define the set \(\mathcal{Y}_{\varepsilon }= \{\mu \in \mathfrak{A}_{*} : \Vert \mu \Vert _{\mathfrak{A}_{*}} \leq \varepsilon \}\). It is a nonempty, closed, bounded, and convex set contained in \(\mathfrak{A}_{*}\). Define \(\mathfrak{N}_{1}\) and \(\mathfrak{N}_{2}\) on \(\mathcal{Y}_{\varepsilon }\) as
and
for \(\mathfrak{t} \in \mathcal{O}\). Let \(\hat{o}= \sup_{\mu \in \mathbb{R}} \psi ( \Vert \mu \Vert _{ \mathfrak{A}_{*}})\). Now, for \(\mu _{1}, \mu _{2} \in \mathcal{Y}_{\varepsilon }\), we obtain inequalities
and
Therefore \(\Vert \mathfrak{N}_{1} \mu _{1}+ \mathfrak{N}_{2} \mu _{2} \Vert _{ \mathfrak{A}_{*}} \leq \hat{o} \Vert \varrho \Vert (\Lambda _{1}^{ \star }+\Lambda _{2}^{\star }) \leq \varepsilon \), which implies that
From the continuity of the single-valued function M it is evident that \(\mathfrak{N}_{1}\) is continuous on its domain. Now, for all \(\mu \in \mathcal{Y}_{\varepsilon }\), we get that
and
Thus
This clearly shows the uniform boundedness of the operator \(\mathfrak{N}_{1}\) on \(\mathcal{Y}_{\varepsilon }\). To ensure the compactness of \(\mathfrak{N}_{1}\) on \(\mathcal{Y}_{\varepsilon }\), consider \(\mathfrak{t}_{1},\mathfrak{t}_{2} \in \mathcal{O}\) such that \(\mathfrak{t}_{1} < \mathfrak{t}_{2}\). Then we get the following inequalities:
Thus, as \(\mathfrak{t}_{1}\) goes to \(\mathfrak{t}_{2}\), \(\vert (\mathfrak{N}_{1} \mu )(\mathfrak{t}_{2}) - ( \mathfrak{N}_{1} \mu )(\mathfrak{t}_{1}) \vert \) tends to zero independently of μ. Also, we find that
Thus \(\vert ({}^{C}\mathfrak{D}_{q}^{\ell _{2} } \mathfrak{N}_{1} \mu )(\mathfrak{t}_{2}) - ({}^{C}\mathfrak{D}_{q}^{\ell _{2} } \mathfrak{N}_{1} \mu )(\mathfrak{t}_{1}) \vert \) goes to zero as \(\mathfrak{t}_{1}\) approaches to \(\mathfrak{t}_{2}\) independently of μ. Therefore \(\Vert (\mathfrak{N}_{1} \mu )(\mathfrak{t}_{2}) - ( \mathfrak{N}_{1} \mu )(\mathfrak{t}_{1}) \Vert _{ \mathfrak{A}_{*}} \to 0\) as \(\mathfrak{t}_{1} \to \mathfrak{t}_{2}\). Consequently, the equicontinuity of the operator \(\mathfrak{N}_{1}\) is confirmed. Therefore by the Arzelà–Ascoli theorem \(\mathfrak{N}_{1}\) is a compact operator on \(\mathcal{Y}_{\varepsilon }\). At last, we show that \(\mathfrak{N}_{2}\) is a contraction mapping. Let \(\mu _{1},\mu _{2} \in \mathcal{Y}_{\varepsilon }\). Then

and

Thus

where the constant \(\mathbb{L} <1\). Therefore \(\mathfrak{N}_{2}\) is a contraction on \(\mathcal{Y}_{\varepsilon }\). Hence Theorem 2.7 implies the existence of a solution for the generalized q-Navier FBVP (3). □
4 Results for q-Navier FBVP (4)
In this section, we obtain the existence results for the generalized q-Navier inclusion FBVP (4). A function μ belonging to \(\mathcal{C}_{\mathfrak{A}_{*}}(\mathcal{O}, \mathfrak{A}_{*})\) is regarded as a solution of the sequential generalized q-Navier FBVP (4) if it fulfills the given BCs and there exists \(\bar{\Phi } \in \mathcal{L}^{1}(\mathcal{O})\) such that \(\bar{\Phi }(\mathfrak{t}) \in \mathfrak{M} (\mathfrak{t}, \mu ( \mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2}} \mu (\mathfrak{t}) )\) for almost all \(\mathfrak{t} \in \mathcal{O}\) and
for all \(\mathfrak{t} \in \mathcal{O}\). We define the set of selections of the multivalued function \(\mathfrak{M}\) by
for \(\mu \in \mathfrak{A}_{*}\). Now we define the operator \(\mathcal{Z}: \mathfrak{A}_{*} \to \mathbb{P}(\mathfrak{A}_{*})\) as
where
For simplicity, put
Theorem 4.1
Let \(\mathfrak{M}:\mathcal{O} \times \mathfrak{A}_{*}^{2} \to \mathbb{P}_{ \mathbb{CM}}(\mathfrak{A}_{*})\) be a multivalued function. Assume that:
- \((\mathfrak{X}_{6})\):
-
the set-valued map \(\mathfrak{M}\) is integrable and bounded such that for all \(\mu _{1}, \mu _{2} \in \mathfrak{A}_{*}\), the map \(\mathfrak{M}(\cdot , \mu _{1}, \mu _{2}): \mathcal{O} \to \mathbb{P}_{ \mathbb{CM}}\) is measurable;
- \((\mathfrak{X}_{7})\):
-
there exist a function \(\zeta \in \mathcal{C}(\mathcal{O}, [0, \infty ))\) and \(\psi \in \Psi \) such that
$$ \mathbb{H}_{\mathrm{d}} \bigl(\mathfrak{M}(\mathfrak{t}, \mu _{1}, \mu _{2}), \mathfrak{M}(\mathfrak{t}, \tilde{\mu _{1}}, \tilde{\mu _{2}}) \bigr) \leq \zeta (\mathfrak{t}) \biggl( \frac{\tilde{\mathfrak{x}}}{ \Vert \zeta \Vert } \biggr) \psi \bigl( \vert \mu _{1}-\tilde{ \mu _{1}} \vert + \vert \mu _{2} - \tilde{\mu _{2}} \vert \bigr){} $$(21)for all \(\mathfrak{t} \in \mathcal{O}\) and \(\mu _{1}, \mu _{2}, \tilde{\mu _{1}}, \tilde{\mu _{2}} \in \mathfrak{A}_{*}\), where \(\sup_{\mathfrak{t}\in \mathcal{O}} \vert \zeta (\mathfrak{t}) \vert = \Vert \zeta \Vert \), \(\tilde{\mathfrak{x}}= \frac{1}{\Lambda _{1}^{\star }+\Lambda _{2}^{\star }}\), and \(\Lambda _{1}^{\star }\), \(\Lambda _{2}^{\star }\) are the constants defined in (15);
- \((\mathfrak{X}_{8})\):
-
there exists a function \(\mathfrak{U}:\mathbb{R}^{2} \times \mathbb{R}^{2} \to \mathbb{R}\) such that \(\mathfrak{U}((\mu _{1}, \mu _{2}), (\tilde{\mu _{1}}, \tilde{\mu _{2}})) \geq 0\) for all \(\mu _{1}, \mu _{2}, \tilde{\mu _{1}}, \tilde{\mu _{2}} \in \mathfrak{A}_{*}\);
- \((\mathfrak{X}_{9})\):
-
if \(\{ \mu _{n} \}_{n \geq 1}\) is a sequence in \(\mathfrak{A}_{*}\) such that \(\mu _{n} \to \mu \) and
$$ \mathfrak{U} \bigl( \bigl(\mu _{n} (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} }\mu _{n}(\mathfrak{t}) \bigr), \bigl(\mu _{n+1} ( \mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu _{n+1}( \mathfrak{t}) \bigr) \bigr) \geq 0{} $$for all \(\mathfrak{t} \in \mathcal{O}\) and \(n \geq 1\), then there exists a subsequence \(\{ \mu _{n_{r}} \}_{r \geq 1}\) of \(\{ \mu _{n} \}\) such that
$$ \mathfrak{U} \bigl( \bigl(\mu _{n_{r}} (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu _{n_{r}}(\mathfrak{t}) \bigr), \bigl( \mu (\mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2} } \mu ( \mathfrak{t}) \bigr) \bigr) \geq 0{} $$for all \(\mathfrak{t} \in \mathcal{O}\) and \(r \geq 1\);
- \((\mathfrak{X}_{10})\):
-
there exist \(\mu _{0} \in \mathfrak{A}_{*}\) and \(\hbar \in \mathcal{Z}(\mu _{0})\) such that
$$ \mathfrak{U} \bigl( \bigl(\mu _{0} (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} }\mu _{0}(\mathfrak{t}) \bigr), \bigl(\hbar (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} } \hbar (\mathfrak{t}) \bigr) \bigr) \geq 0{} $$for all \(\mathfrak{t} \in \mathcal{O}\), where the multifunction \(\mathcal{Z}: \mathfrak{A}_{*} \to \mathbb{P}(\mathfrak{A}_{*})\) is defined in (19);
- \((\mathfrak{X}_{11})\):
-
for any \(\mu \in \mathfrak{A}_{*}\) and \(\hbar \in \mathcal{Z}(\mu )\) such that
$$ \mathfrak{U} \bigl( \bigl(\mu (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} }\mu (\mathfrak{t}) \bigr), \bigl(\hbar ( \mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\hbar ( \mathfrak{t}) \bigr) \bigr) \geq 0, $$there exists \(\check{\omega } \in \mathcal{Z}(\mu )\) such that
$$ \mathfrak{U} \bigl( \bigl(\hbar (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{ \ell _{2} }\hbar (\mathfrak{t}) \bigr), \bigl( \check{\omega } ( \mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2} } \check{\omega }( \mathfrak{t}) \bigr) \bigr) \geq 0{} $$for each \(\mathfrak{t} \in \mathcal{O}\).
Then the fractional q-Navier inclusion FBVP (4) admits a solution.
Proof
Clearly, any solution of the fractional q-Navier FBVP (4) is a fixed point of the map \(\mathcal{Z}: \mathfrak{A}_{*} \to \mathbb{P}(\mathfrak{A}_{*})\). Since the set-valued map \(\mathfrak{t} \to \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) admits closed values and is measurable for all \(\mu \in \mathfrak{A}_{*}\), \(\mathfrak{M}\) admits a measurable selection. This indicates that the set \((\mathbb{SEL})_{\mathfrak{M}, \mu }\neq \emptyset \). Firstly, we prove that the set \(\mathcal{Z}(\mu )\) contained in \(\mathfrak{A}_{*}\) is closed for any \(\mu \in \mathfrak{A}_{*}\). Suppose \(\{ \mu _{n} \}_{n \geq 1}\) is a sequence in \(\mathcal{Z}(\mu )\) such that \(\mu _{n} \to \mu \). For each n, there exists \(\bar{\Phi }_{n} \in (\mathbb{SEL})_{\mathfrak{M}, \mu }\) such that
for almost all \(\mathfrak{t} \in \mathcal{O}\). Since the map \(\mathfrak{M}\) is compact-valued, there is a subsequence of \(\{ \bar{\Phi }_{n} \}_{n \geq 1}\) converging to some \(\bar{\Phi } \in \mathcal{L}^{1} (\mathcal{O})\). Hence \(\bar{\Phi } \in (\mathbb{SEL})_{\mathfrak{M}, \mu }\), and
for each \(\mathfrak{t} \in \mathcal{O}\). This reveals that \(\mu \in \mathcal{Z}(\mu )\), and hence \(\mathcal{Z}\) admits closed values. As the multivalued map \(\mathfrak{M}\) has compact values, it is easy to conclude that \(\mathcal{Z}(\mu )\) is bounded for each \(\mu \in \mathfrak{A}_{*}\). Let us show that the multifunction \(\mathcal{Z}\) is an α-ψ-contraction. To this end, we define the nonnegative function α on \(\mathfrak{A}_{*} \times \mathfrak{A}_{*}\) by
for all \(\mu , \tilde{\mu } \in \mathfrak{A}_{*}\). Let \(\mu , \tilde{\mu } \in \mathfrak{A}_{*}\) and \(\hbar _{1} \in \mathcal{Z}(\tilde{\mu })\). Consider \(\bar{\Phi }_{1} \in (\mathbb{SEL})_{\mathfrak{M}, \tilde{\mu }}\) such that
for all \(\mathfrak{t} \in \mathcal{O}\). From (21) we have
for any \(\mu , \tilde{\mu } \in \mathfrak{A}_{*}\) such that
for almost all \(\mathfrak{t} \in \mathcal{O}\). Hence there exists \(\check{\omega } \in \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) such that
Consider \(\mathfrak{T}: \mathcal{O} \to \mathbb{P}(\mathfrak{A}_{*})\) defined by
for \(\mathfrak{t} \in \mathcal{O}\). Since \(\bar{\Phi }_{1}\) and \(\vartheta = \zeta ( \frac{\tilde{\mathfrak{x}}}{\Vert \zeta \Vert } ) \psi ( \vert \mu - \tilde{\mu } \vert + \vert {}^{C}\mathfrak{D}_{q}^{ \ell _{2} }\mu - {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\tilde{\mu } \vert )\) are measurable, the multifunction \(\mathfrak{T} (\cdot )\cap \mathfrak{M} (\cdot , \mu (\cdot ), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu (\cdot ) )\) is measurable. Now select \(\bar{\Phi }_{2} \in \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) such that for all \(\mathfrak{t} \in \mathcal{O}\),
Consider \(\hbar _{2} \in \mathcal{Z}(\mu )\) given as
for \(\mathfrak{t} \in \mathcal{O}\). Then we obtain
and
for all \(\mathfrak{t} \in \mathcal{O}\). Hence we find that
Therefore \(\alpha (\mu , \tilde{\mu }) \mathbb{H}_{\mathrm{d}} ( \mathcal{Z} ( \mu ) - \mathcal{Z}(\tilde{\mu }) ) \leq \psi ( \Vert \mu - \tilde{\mu } \Vert _{\mathfrak{A}_{*}} )\) for all \(\mu , \tilde{\mu } \in \mathfrak{A}_{*}\), and we deduce that the multifunction \(\mathcal{Z}\) is an α-ψ-contraction. Now let \(\mu \in \mathfrak{A}_{*}\) and \(\tilde{\mu } \in \mathcal{Z} (\mu )\) be such that \(\alpha (\mu , \tilde{\mu }) \geq 1\) and
so that there exists a function \(\check{\omega } \in \mathcal{Z}(\tilde{\mu })\) such that
Thus \(\alpha (\tilde{\mu }, \check{\omega }) \geq 1\), and it follows that \(\mathcal{Z}\) is α-admissible. Now consider \(\mu _{0} \in \mathfrak{A}_{*}\) and \(\tilde{\mu } \in \mathcal{Z}(\mu _{0})\) such that for all \(\mathfrak{t} \in \mathcal{O}\),
Then we get \(\alpha (\mu _{0}, \tilde{\mu }) \geq 1\). Let \(\{ \mu _{n} \}_{n \geq 1}\) be a sequence in \(\mathfrak{A}_{*}\) such that \(\mu _{n} \to \mu \) and \(\alpha (\mu _{n}, \mu _{n+1}) \geq 1\) for all n. Then
By \((\mathfrak{X}_{9})\) there exists a subsequence \(\{ \mu _{n_{r}} \}_{r\geq 1}\) of \(\{ \mu _{n} \}\) such that
for all \(\mathfrak{t} \in \mathcal{O}\). This implies that \(\alpha (\mu _{n_{r}}, \mu ) \geq 1\) for all r. Hence all the assumptions of Theorem 2.8 are fulfilled. This confirms the existence of a fixed–point of the operator \(\mathcal{Z}\). Therefore it follows that the generalized q-Navier FBVP (4) has a solution. □
Theorem 4.2
Let \(\mathfrak{M}:\mathcal{O} \times \mathfrak{A}_{*}^{2} \to \mathbb{P}_{ \mathbb{CM}}(\mathfrak{A}_{*})\) be a multivalued map. In addition, suppose that:
- \((\mathfrak{X}_{12})\):
-
there exists a nondecreasing and u.s.c function \(\psi : [0, \infty ) \to [0, \infty )\) such that \(\liminf_{\mathfrak{t} \to \infty } (\mathfrak{t} - \psi ( \mathfrak{t})) \geq 0\) and \(\psi (\mathfrak{t}) \leq \mathfrak{t}\) for all \(\mathfrak{t} >0\);
- \((\mathfrak{X}_{13})\):
-
the multifunction \(\mathfrak{M}:\mathcal{O} \times \mathfrak{A}_{*}^{2} \to \mathbb{P}_{ \mathbb{CM}}(\mathfrak{A}_{*})\) is an integrable bounded operator such that \(\mathfrak{M}( \cdot , \mu _{1}, \mu _{2} ):\mathcal{O} \to \mathbb{P}_{\mathbb{CM}}(\mathfrak{A}_{*})\) is measurable for all \(\mu _{1}, \mu _{2} \in \mathfrak{A}_{*}\);
- \((\mathfrak{X}_{14})\):
-
there exists a nonnegative map \(\zeta \in \mathcal{C}(\mathcal{O}, [0, \infty ))\) such that
$$ \mathbb{H}_{\mathrm{d}} \bigl(\mathfrak{M}(\mathfrak{t}, \mu _{1}, \mu _{2}), \mathfrak{M}(\mathfrak{t}, \tilde{\mu _{1}}, \tilde{\mu _{2}}) \bigr) \leq \zeta (\mathfrak{t}) \tilde{\mathfrak{x}}_{\star } \psi \bigl( \vert \mu _{1}- \tilde{\mu _{1}} \vert + \vert \mu _{2}-\tilde{\mu _{2}} \vert \bigr){} $$(22)for all \(\mathfrak{t} \in \mathcal{O}\) and \(\mu _{1}, \mu _{2}, \tilde{\mu _{1}}, \tilde{\mu _{2}} \in \mathfrak{A}_{*}\), where \(\tilde{\mathfrak{x}}_{\star }= \frac{1}{\chi _{1} + \chi _{2}}\) with constants \(\chi _{1}\), \(\chi _{2}\) defined in (20);
- \((\mathfrak{X}_{15})\):
-
the operator \(\mathcal{Z}\) defined in (19) has the approximate end-point criterion.
Then the generalized q-Navier inclusion BVP (4) has a solution.
Proof
We claim the existence of an end-point for \(\mathcal{Z}: \mathfrak{A}_{*} \to \mathbb{P}(\mathfrak{A}_{*})\). Firstly, we show that the set \(\mathcal{Z}(\mu )\) contained in \(\mathfrak{A}_{*}\) is closed for any \(\mu \in \mathfrak{A}_{*}\). Since the set-valued map \(\mathfrak{t} \to \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) admits closed values and is measurable for all \(\mu \in \mathfrak{A}_{*}\), \(\mathfrak{M}\) has a measurable selection. This indicates that the set \((\mathbb{SEL})_{\mathfrak{M}, \mu }\neq \emptyset \). As shown in the proof of Theorem 4.1, we can prove that \(\mathcal{Z}(\mu )\) has closed values. Also, we can easily get that \(\mathcal{Z}(\mu )\) is bounded for each \(\mu \in \mathfrak{A}_{*}\) because the multivalued map \(\mathfrak{M}\) has compact values. Now let us prove the inequality \(\mathbb{H}_{\mathrm{d}} (\mathcal{Z}(\mu ), \mathcal{Z}( \check{\omega }) ) \leq \psi ( \Vert \mu - \check{\omega } \Vert _{ \mathfrak{A}_{*}})\). To this end, let \(\mu , \check{\omega } \in \mathfrak{A}_{*}\) and \(\hbar _{1} \in \mathcal{Z}(\check{\omega }) \), and select \(\bar{\Phi }_{1} \in (\mathbb{SEL})_{\mathfrak{M}, \check{\omega }}\) such that
for almost all \(\mathfrak{t} \in \mathcal{O}\). From (22) we have
for all \(\mathfrak{t} \in \mathcal{O}\). Hence there exists \(\bar{\rho } \in \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) such that
Now we define the set-valued map \(\Upsilon : \mathcal{O} \to \mathbb{P}(\mathfrak{A}_{*})\) by
for \(\mathfrak{t} \in \mathcal{O}\). Since \(\bar{\Phi }_{1}\) and \(\sigma _{*} = \zeta \tilde{\mathfrak{x}}_{\star } \psi ( \vert \mu - \check{\omega } \vert + \vert {}^{C}\mathfrak{D}_{q}^{\ell _{2}}\mu - {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\check{\omega } \vert )\) are measurable, the multifunction \(\Upsilon (\cdot )\cap \mathfrak{M} (\cdot , \mu (\cdot ), {}^{C} \mathfrak{D}_{q}^{\ell _{2} }\mu (\cdot ) )\) is measurable. Next, we choose \(\bar{\Phi }_{2} \in \mathfrak{M} (\mathfrak{t}, \mu (\mathfrak{t}), {}^{C}\mathfrak{D}_{q}^{\ell _{2} }\mu (\mathfrak{t}) )\) such that
for all \(\mathfrak{t} \in \mathcal{O}\). Choose \(\hbar _{2} \in \mathcal{Z}(\mu )\) such that
for all \(\mathfrak{t} \in \mathcal{O}\). By continuing the similar steps implemented in Theorem 4.1 we obtain
Therefore \(\mathbb{H}_{\mathrm{d}} ( \mathcal{Z} (\mu ) , \mathcal{Z}( \check{\omega }) ) \leq \psi ( \Vert \mu - \check{\omega } \Vert _{ \mathfrak{A}_{*}})\) for all \(\mu , \check{\omega } \in \mathfrak{A}_{*}\). By \((\mathfrak{X}_{15})\) \(\mathcal{Z}\) involves an approximate end-point criterion. Now Theorem 2.9 indicates the existence of \(\mu ^{**} \in \mathfrak{A}_{*}\) such that \(\mathcal{Z}(\mu ^{**})= \{ \mu ^{**} \}\). Hence the fractional q-Navier inclusion BVP (4) has a solution \(\mu ^{**}\). □
5 Examples
We provide a few illustrative numerical examples to our theoretical and analytical findings in the previous sections.
Example 5.1
Consider the generalized q-Navier FBVP
where \(q=0.57\), \(\ell _{1}= 1.35\), \(\ell _{2}= 1.68\), \(\gamma = 9.61\), \(\delta = 16.37\), \(\lambda = 21.49\), \(\beta = 7.15\), and \(\mathfrak{t} \in \mathcal{O}\). Also, consider the continuous mapping \(M: \mathcal{O} \times \mathbb{R}^{2} \to \mathbb{R}\) defined by
For any \(\mu _{1}, \mu _{2}, w_{1}, w_{2} \in \mathbb{R}\), we can write
Put  for all \(\mathfrak{t}\). Then
for all \(\mathfrak{t}\). Then  . Moreover, consider the nondecreasing continuous map \(\psi : \mathbb{R}^{+} \to \mathbb{R}^{+}\) given by \(\psi (\varsigma )=\varsigma \) for all \(\varsigma \in \mathbb{R}^{+}\). Then we obtain
. Moreover, consider the nondecreasing continuous map \(\psi : \mathbb{R}^{+} \to \mathbb{R}^{+}\) given by \(\psi (\varsigma )=\varsigma \) for all \(\varsigma \in \mathbb{R}^{+}\). Then we obtain
Clearly, the function \(\varrho : \mathcal{O} \to \mathbb{R}^{+}\) defined by \(\varrho (\mathfrak{t})= \frac{\mathfrak{t}}{27}\) is continuous. By (16) we find that
Now by (17) \(\mathbb{L} \approx 0.0738194 < 1\). Hence by Theorem 3.3 we can conclude that the fractional generalized sequential q-Navier BVP (23) has a solution.
Example 5.2
Consider the generalized q-Navier inclusion FBVP
where \(q=0.26\), \(\ell _{1}= 1.41\), \(\ell _{2}= 1.88\), \(\gamma = 10.46\), \(\delta = 53.17\), \(\lambda = 11.73\), \(\beta = 95.31\), and \(\mathfrak{t} \in \mathcal{O}\). Define \(\mathfrak{M}: \mathcal{O} \times \mathbb{R}^{2} \to \mathbb{P}( \mathbb{R})\) by
for \(\mathfrak{t} \in \mathcal{O}\). Now select a nonnegative map \(\zeta \in \mathcal{C}(\mathcal{O}, [0, \infty ))\) such that \(\zeta (\mathfrak{t}) = \frac{\mathfrak{t}}{7}\) for each \(\mathfrak{t} \in \mathcal{O}\). Thus \(\Vert \zeta \Vert = \sup_{\mathfrak{t} \in \mathcal{O}} \vert \frac{\mathfrak{t}}{7} \vert = \frac{1}{7}\). Furthermore, consider the nonnegative nondecreasing u.s.c map \(\psi : [0, \infty ) \to [0, \infty )\) defined as \(\psi (\mathfrak{t}) = \frac{\mathfrak{t}}{5}\) for all \(\mathfrak{t} >0\). It is easy to find that \(\liminf_{\mathfrak{t} \to \infty } (\mathfrak{t} - \psi ( \mathfrak{t})) >0\) and \(\psi (\mathfrak{t}) < \mathfrak{t}\) for all \(\mathfrak{t} >0\). Now by (15) and (20) we get
and
For every \(\mu _{1}, \mu _{2}, \tilde{\mu _{1}}, \tilde{\mu _{2}} \in \mathbb{R}\), we have
Next, we consider the set-valued map \(\mathcal{Z}: \mathfrak{A}_{*} \to \mathbb{P}(\mathfrak{A}_{*})\) defined as
where
Ultimately, by Theorem 4.2 we find that the generalized q-Navier BVP (24) has a solution.
6 Conclusion
In this paper, we modeled the standard Navier equation to q-fractional Navier BVP and explored the existence of solutions by making use of the well-known results from functional analysis due to some techniques introduced by Krasnoselskii, Samet, Mohammadi, and Amini-Harandi based on special operators. In fact, by deriving an integral equation we defined some operators based on it, and then by utilizing a subclass of special operators such as orbital α-admissible maps, α-ψ-contractions, the multifunctions having approximate endpoint criterion, and so on we proved the required results. Finally, we gave illustrations by two examples to explain the consistency of the findings for the proposed sequential generalized Navier q-BVP. As a possible future plan, some other operators may be considered in the next papers to discuss the existence of solutions, stability, and other qualitative aspects of solutions of the generalized Navier fractional model in two singular or nonsingular formats.
Availability of data and materials
Data sharing not applicable to this paper as no datasets were generated or analyzed during the current study.
References
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Baleanu, D., Etemad, S., Rezapour, S.: A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020, 64 (2020). https://doi.org/10.1186/s13661-020-01361-0
Baleanu, D., Etemad, S., Rezapour, S.: On a fractional hybrid integro-differential equation with mixed hybrid integral boundary value conditions by using three operators. Alex. Eng. J. 59(5), 3019–3027 (2020). https://doi.org/10.1016/j.aej.2020.04.053
Alam, M., Zada, A., Popa, L.L., Kheiryan, A., Rezapour, S., Kaabar, M.K.A.: A fractional differential equation with multi-point strip boundary condition involving the Caputo fractional derivative and its Hyers-Ulam stability. Bound. Value Probl. 2021, 73 (2021). https://doi.org/10.1186/s13661-021-01549-y
Thabet, S.T.M., Etemad, S., Rezapour, S.: On a coupled Caputo conformable system of pantograph problems. Turk. J. Math. 45(1), 496–519 (2021). https://doi.org/10.3906/mat-2010-70
Adiguzel, R.S., Aksoy, U., Karapinar, E., Erhan, I.M.: On the solutions of fractional differential equations via Geraghty type hybrid contractions. Int. J. Appl. Comput. Math. 20(2), 313–333 (2021)
Marasi, H., Afshari, H., Daneshbastam, M., Zhai, C.B.: Fixed points of mixed monotone operators for existence and uniqueness of nonlinear fractional differential equations. J. Contemp. Math. Anal. 52, 8–13 (2017). https://doi.org/10.3103/S1068362317010022
Afshari, H., Gholamyan, H., Zhai, C.B.: New applications of concave operators to existence and uniqueness of solutions for fractional differential equations. Math. Commun. 25(1), 157–169 (2020)
Baleanu, D., Rezapour, S., Saberpour, Z.: On fractional integro-differential inclusions via the extended fractional Caputo–Fabrizio derivation. Bound. Value Probl. 2019, 79 (2019). https://doi.org/10.1186/s13661-019-1194-0
Aydogan, S.M., Baleanu, D., Mousalou, A., Rezapour, S.: On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018, 90 (2018). https://doi.org/10.1186/s13661-018-1008-9
Baleanu, D., Mousalou, A., Rezapour, S.: On the existence of solutions for some infinite coefficient-symmetric Caputo–Fabrizio fractional integro-differential equations. Bound. Value Probl. 2017, 145 (2017). https://doi.org/10.1186/s13661-017-0867-9
Jackson, F.H.: q-difference equations. Am. J. Math. 32(4), 305–314 (1910). https://doi.org/10.2307/2370183
Al-Salam, W.A.: q-analogues of Cauchy’s formula. Proc. Am. Math. Soc. 17(3), 182–184 (1952). https://doi.org/10.2307/2035378
Agarwal, R.P.: Certain fractional q-integrals and q-derivatives. Math. Proc. Camb. Philos. Soc. 66(2), 365–370 (1969). https://doi.org/10.1017/S0305004100045060
Ahmad, B., Etemad, S., Ettefagh, M., Rezapour, S.: On the existence of solutions for fractional q-difference inclusions with q-antiperiodic boundary conditions. Bull. Math. Soc. Sci. Math. Roum. 59(107)(2), 119–134 (2016)
Al-Salam, W.A.: Some fractional q-integrals and q-derivatives. Proc. Edinb. Math. Soc. 15(2), 135–140 (1969). https://doi.org/10.1017/S0013091500011469
Abdeljawad, T., Baleanu, D.: Caputo q-fractional initial value problems and a q-analogue Mittag-Leffler function. Commun. Nonlinear Sci. Numer. Simul. 16(12), 4682–4688 (2011). https://doi.org/10.1016/j.cnsns.2011.01.026
Li, Y., Liu, J., O’Regan, D., Xu, J.: Nontrivial solutions for a system of fractional q-difference equations involving q-integral boundary conditions. Mathematics 8(5), 828 (2020). https://doi.org/10.3390/math8050828
Etemad, S., Ntouyas, S.K., Ahmad, B.: Existence theory for a fractional q-integro-difference equation with q-integral boundary conditions of different orders. Mathematics 7(8), 659 (2016). https://doi.org/10.3390/math7080659
Asawasamrit, S., Tariboon, J., Ntouyas, S.K.: Existence of solutions for fractional q-integro-difference equations with nonlocal fractional q-integral conditions. Abstr. Appl. Anal. 2014, Article ID 474138 (2014). https://doi.org/10.1155/2014/474138
Etemad, S., Rezapour, S., Samei, M.E.: α-ψ-contractions and solutions of a q-fractional differential inclusion with three-point boundary value conditions via computational results. Adv. Differ. Equ. 2020, 218 (2020). https://doi.org/10.1186/s13662-020-02679-w
Sitthiwirattham, T.: On nonlocal fractional q-integral boundary value problems of fractional q-difference and fractional q-integro-difference equations involving different numbers of order and q. Bound. Value Probl. 2016, 12 (2016). https://doi.org/10.1186/s13661-016-0522-x
Rezapour, S., Samei, M.E.: On the existence of solutions for a multi-singular pointwise defined fractional q-integro-differential equation. Bound. Value Probl. 2020, 38 (2020). https://doi.org/10.1186/s13661-020-01342-3
Sitho, S., Sudprasert, C., Ntouyas, S.K., Tariboon, J.: Noninstantaneous impulsive fractional quantum Hahn integro-difference boundary value problems. Mathematics 8(5), 671 (2020). https://doi.org/10.3390/math8050671
Abdeljawad, T., Agarwal, R.P., Karapinar, E., Kumari, P.S.: Solutions of the nonlinear integral equation and fractional differential equation using the technique of a fixed point with a numerical experiment in extended b-metric space. Symmetry 11(5), 686 (2019). https://doi.org/10.3390/sym11050686
Alizadeh, S., Baleanu, D., Rezapour, S.: Analyzing transient response of the parallel RCL circuit by using the Caputo-Fabrizio fractional derivative. Adv. Differ. Equ. 2020, 55 (2020). https://doi.org/10.1186/s13662-020-2527-0
Bachir, F.S., Abbas, S., Benbachir, M., Benchora, M.: Hilfer–Hadamard fractional differential equations; existence and attractivity. Adv. Theory Nonlinear Anal. Appl. 5(1), 49–57 (2021). https://doi.org/10.31197/atnaa.848928
Noeiaghdam, Z., Allahviranloo, T., Nieto, J.J.: q-Fractional differential equations with uncertainty. Soft Comput. 23, 9507–9524 (2019). https://doi.org/10.1007/s00500-019-03830-w
Rezapour, S., Imran, A., Hussain, A., Martinez, F., Etemad, S., Kaabar, M.K.A.: Condensing functions and approximate endpoint criterion for the existence analysis of quantum integro-difference FBVPs. Symmetry 13(3), 469 (2021). https://doi.org/10.3390/sym13030469
Ferreira, R.A.C.: Positive solutions for a class of boundary value problems with fractional q-differences. Comput. Math. Appl. 61(2), 367–373 (2011). https://doi.org/10.1016/j.camwa.2010.11.012
Ahmad, B., Ntouyas, S.K.: Boundary value problems for q-difference inclusions. Abstr. Appl. Anal. 2011, Article ID 292860 (2011). https://doi.org/10.1155/2011/292860
Reiss, E.L., Callegari, A.J., Ahluwalia, D.S.: Ordinary Differential Equations with Applications. Holt, Rinehart & Winston, New York (1978)
Aftabizadeh, A.R.: Existence and uniqueness theorems for fourth-order boundary value problems. J. Math. Anal. Appl. 116(2), 415–426 (1986). https://doi.org/10.1016/S0022-247X(86)80006-3
Ma, R., Zhang, J., Fu, S.: Existence and uniqueness theorems for fourth-order boundary value problems. J. Math. Anal. Appl. 215(2), 415–422 (1997). https://doi.org/10.1006/jmaa.1997.5639
Bai, Z., Ge, W., Wang, Y.: The method of lower and upper solutions for some fourth-order equations. J. Inequal. Pure Appl. Math. 5(1), 13 (2004)
Bachar, I., Eltayeb, H.: Existence and uniqueness results for fractional Navier boundary value problems. Adv. Differ. Equ. 2020, 609 (2020). https://doi.org/10.1186/s13662-020-03071-4
Smart, D.R.: Fixed Point Theorems. Cambridge University Press, Cambridge (1980)
Samet, B., Vetro, C., Vetro, P.: Fixed point theorems for α-ψ-contractive type mappings. Nonlinear Anal., Theory Methods Appl. 75(4), 2154–2165 (2018). https://doi.org/10.1016/j.na.2011.10.014
Mohammadi, B., Rezapour, S., Shahzad, N.: Some results on fixed points of α-ψ-Ciric generalized multifunctions. Fixed Point Theory Appl. 2013, 24 (2013). https://doi.org/10.1186/1687-1812-2013-24
Rajkovic, P.M., Marinkovic, S.D., Stankovic, M.S.: Fractional integrals and derivatives in q-calculus. Appl. Anal. Discrete Math. 1(1), 311–323 (2007)
Jackson, F.H.: On q-definite integrals. Q. J. Pure Appl. Math. 41, 193–203 (1910)
Adams, C.R.: The general theory of a class of linear partial q-difference equations. Trans. Am. Math. Soc. 26(3), 283–312 (1924). https://doi.org/10.2307/1989141
Graef, J.R., Kong, L.: Positive solutions for a class of higher order boundary value problems with fractional q-derivatives. Appl. Math. Comput. 218(19), 9682–9689 (2012). https://doi.org/10.1016/j.amc.2012.03.006
El-Shahed, M., Al-Askar, F.: Positive solutions for boundary value problem of nonlinear fractional q-difference equation. Int. Sch. Res. Not. 218, 1–12 (2011). https://doi.org/10.5402/2011/385459
Popescu, O.: Some new fixed point theorems for α-Geraghty contraction type maps in metric spaces. Fixed Point Theory Appl. 2014, 190 (2014). https://doi.org/10.1186/1687-1812-2014-190
Arshad, M., Ameer, E., Karapinar, E.: Generalized contractions with triangular α-orbital admissible mapping on Branciari metric spaces. J. Inequal. Appl. 2016, 63 (2016). https://doi.org/10.1186/s13660-016-1010-7
Aksoy, U., Karapinar, E., Erhan, I.M.: Fixed points of generalized α-admissible contractions on b-metric spaces with an application to boundary value problems. J. Nonlinear Convex Anal. 17(6), 1095–1108 (2016)
Aydi, H., Karapinar, E., Yazidi, H.: Modified f-contractions via α-admissible mappings and applications to integral equations. Filomat 31(5), 1141–1148 (2017). https://doi.org/10.2298/FIL1705141A
Aydi, H., Karapinar, E., Zhang, D.: A note on generalized admissible-Meir–Keeler-contractions in the context of generalized metric spaces. Results Math. 71(5), 73–92 (2017). https://doi.org/10.1007/s00025-015-0516-5
Amini-Harandi, A.: Endpoints of set-valued contractions in metric spaces. Nonlinear Anal., Theory Methods Appl. 72(1), 132–134 (2010). https://doi.org/10.1016/j.na.2009.06.074
Acknowledgements
The first and sixth authors were supported by Azarbaijan Shahid Madani University. The authors express their gratitude to unknown referees for their helpful suggestions, which improved the final version of this paper.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Etemad, S., Ntouyas, S.K., Imran, A. et al. Application of some special operators on the analysis of a new generalized fractional Navier problem in the context of q-calculus. Adv Differ Equ 2021, 402 (2021). https://doi.org/10.1186/s13662-021-03558-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03558-8
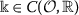 such that for all
such that for all 