- Research
- Open access
- Published:
On interpolative contractions that involve rational forms
Advances in Difference Equations volume 2021, Article number: 448 (2021)
Abstract
The aim of this paper is to investigate the interpolative contractions involving rational forms in the framework of b-metric spaces. We prove the existence of a fixed point of such a mapping with different combinations of the rational forms. A certain example is considered to indicate the validity of the observed result.
1 Introduction and preliminaries
It is worth noting that Caccioppoli [1] is the first author who extended the results of Banach [2] from normed space to metric space. After that, a number of authors have studied different abstract spaces to advance the Banach and Caccioppoli results. One of the successive generalizations was given Bakhtin [3] (and independently by Czerwik [4]) from metric space to b-metric space. Following this success, many authors have continued to work on this trend and reported several improvements, advances in the setting of b-metric spaces, see e.g. [5–12].
Let  be a nonempty set and
be a nonempty set and  be a metric on
be a metric on  . The notion of b-metric (reported in several papers, e.g., Bakhtin [3], Czerwik [4]) as an extension of a metric notion is obtained by replacing the triangle inequality of the metric with a general one
. The notion of b-metric (reported in several papers, e.g., Bakhtin [3], Czerwik [4]) as an extension of a metric notion is obtained by replacing the triangle inequality of the metric with a general one
- \((B)\):
-
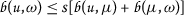 for every
for every 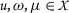 ,
,
for fixed \(s \geq 1\). The triplet  is said to be a b-metric space. (It is worth pointing out that in case \(s=1\) the space
is said to be a b-metric space. (It is worth pointing out that in case \(s=1\) the space  coincides with a corresponding standard metric space.)
coincides with a corresponding standard metric space.)
One of the basic examples for b-metric is the following.
Example
([5])
Let  be a metric space. Then the function
be a metric space. Then the function  defined as
defined as  with \(p>1\) forms a b-metric (here \(s=2^{p-1}\)).
with \(p>1\) forms a b-metric (here \(s=2^{p-1}\)).
For more examples, see e.g. [5–12].
Like metric spaces, b-metric spaces admit a nice topology. On the other hand, alike metric, b-metric does not need to be continuous. For the sake of the integrity of the article, we recollect the basic topological notions here.
We say that a sequence  in a b-metric space
in a b-metric space  is
is
-
(1)
convergent to
 if
if 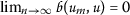 . The limit of a convergent sequence is unique;
. The limit of a convergent sequence is unique; -
(2)
Cauchy if
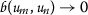 as \(n,m\rightarrow \infty \).
as \(n,m\rightarrow \infty \).
Each convergent sequence in a b-metric space is Cauchy and, as usual, if each Cauchy sequence is convergent, then the b-metric space  is said to be complete.
is said to be complete.
Definition 1.1
Let  be a b-metric space and
be a b-metric space and  be a mapping. For
be a mapping. For  , the orbit of
, the orbit of  at
at  is the set
is the set

The mapping  is said to be orbitally continuous at a point
is said to be orbitally continuous at a point  if
if

Additionally, if every Cauchy sequence  is convergent in
is convergent in  , then the b-metric space
, then the b-metric space  is said to be
is said to be  -orbitally complete.
-orbitally complete.
Definition 1.2
([13])
Let  be a b-metric space. We say that the mapping
be a b-metric space. We say that the mapping  is m-continuous, where \(m=1,2,\ldots\) , if
is m-continuous, where \(m=1,2,\ldots\) , if  , whenever the sequence
, whenever the sequence  in
in  is such that
is such that  .
.
Remark 1.3
We note that every continuous mapping is orbitally continuous in  and also every complete b-metric space is
and also every complete b-metric space is  -orbitally complete for any
-orbitally complete for any  , but the converse is not necessarily true.
, but the converse is not necessarily true.
On the other hand, it is clear that 1-continuity (which coincides with usual continuity) implies 2-continuity implies 3-continuity and so on, but the converse does not hold. Indeed, for example, considering the mapping  , where
, where  , defined by
, defined by

we can easily see that  is not continuous (in
is not continuous (in  ), but it is 2-continuous because
), but it is 2-continuous because  .
.
Let us consider the following class of functions (named the set of b-comparison functions):
here \(\phi ^{n}\) represents the nth iterate of ϕ. It can be shown that every function \(\phi \in \Theta \) fulfills the following properties:
- \((\phi 1)\):
-
\(\phi (\theta )<\theta \) for any \(\theta >0\);
- \((\phi 2)\):
-
\(\phi (0)=0\).
Let  be a nonempty set and \(\alpha :\mathcal{X}\times \mathcal{X}\rightarrow [0,\infty )\) be a function. We say that the mapping
be a nonempty set and \(\alpha :\mathcal{X}\times \mathcal{X}\rightarrow [0,\infty )\) be a function. We say that the mapping  is α-orbital admissible if
is α-orbital admissible if

for all  .
.
Moreover, we say that the b-metric space  is α-regular if for any sequence \(\{ \eta _{m} \} \) in
is α-regular if for any sequence \(\{ \eta _{m} \} \) in  such that \(\lim_{m\rightarrow \infty }\eta _{m}=\eta \) and \(\alpha (\eta _{m}, \eta _{m+1})\geq 1\) we have \(\alpha (\eta _{m},\eta )\geq 1\).
such that \(\lim_{m\rightarrow \infty }\eta _{m}=\eta \) and \(\alpha (\eta _{m}, \eta _{m+1})\geq 1\) we have \(\alpha (\eta _{m},\eta )\geq 1\).
(For more details and examples, see [14].)
Very recently, the notion of the interpolative contraction was introduced in [15]. The goal of this paper is to revisit the well-known Kannan type contraction in the setting of interpolation. After that, several famous contractions (Ćirić [16], Reich [17], Rus [18], Hardy– Rogers [19], Kannan [20], Bianchini [21]) are revisited in this new setting, see e.g. [15, 22–26]
In this paper, we combine all these notions and trends to get more general results on the topic in the literature. We observe some interpolative contractions involving distinct rational forms that provide a fixed point in the framework of b-metric spaces.
2 Main results
Definition 2.1
Let  be a b-metric space. A self-mapping
be a b-metric space. A self-mapping  is called
is called  -admissible interpolative contraction (\(l=1,2\)) if there exist \(\phi \in \Theta \) and
-admissible interpolative contraction (\(l=1,2\)) if there exist \(\phi \in \Theta \) and  such that
such that

where  , \(i=1, 2, 3, 4, 5\), are such that
, \(i=1, 2, 3, 4, 5\), are such that  and
and

and

for any  . (
. ( .)
.)
The first main results of this paper is given in the following theorem.
Theorem 2.2
Let  be a complete b-metric space and
be a complete b-metric space and  be an
be an  -admissible interpolative contraction such that
-admissible interpolative contraction such that
- \((i)\):
-
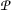 is α-orbital admissible;
is α-orbital admissible; - \((\mathit{ii})\):
-
there exists
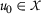 such that
such that 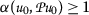 ;
; - \((\mathit{iii}_{1})\):
-
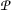 is m-continuous for \(m\geq 1\), or
is m-continuous for \(m\geq 1\), or - \((\mathit{iii}_{2})\):
-
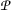 is orbitally continuous.
is orbitally continuous.
Then  possesses a fixed point
possesses a fixed point  and the sequence
and the sequence  converges to this point ϖ.
converges to this point ϖ.
Proof
Let  in
in  be an arbitrary point and the sequence \(\{ \eta _{n} \} \) be defined as
be an arbitrary point and the sequence \(\{ \eta _{n} \} \) be defined as  ,
,  for all \(n\in \mathbb{N}\). If we can find some \(q\in \mathbb{N}\) such that
for all \(n\in \mathbb{N}\). If we can find some \(q\in \mathbb{N}\) such that  , then it follows that \(\eta _{q}\) is a fixed point of
, then it follows that \(\eta _{q}\) is a fixed point of  and the proof is closed. For this reason, we can assume from now on that \(\eta _{n}\neq \eta _{n-1}\) for any \(n\in \mathbb{N}\). Using assumption \((i)\),
and the proof is closed. For this reason, we can assume from now on that \(\eta _{n}\neq \eta _{n-1}\) for any \(n\in \mathbb{N}\). Using assumption \((i)\),  is α-orbital admissible, we have
is α-orbital admissible, we have

On the other hand, we have that

Now, taking into account the main assumption that  is an
is an  -admissible interpolative contraction, if we substitute
-admissible interpolative contraction, if we substitute  with \(\eta _{n-1}\) and ω with \(\eta _{n}\) in (2.1), we get
with \(\eta _{n-1}\) and ω with \(\eta _{n}\) in (2.1), we get

But by \((B)\), together with the monotony of the function ϕ, it follows

moreover, by \((\phi 1)\) we have

If there exists \(m_{0}\in \mathbb{N}\) such that  , then the above inequality becomes
, then the above inequality becomes

which is a contradiction since (keeping in mind that  ) it is equivalent with
) it is equivalent with

Therefore, for any \(n\in \mathbb{N}\),

Furthermore, returning to inequality (2.5), we have

Let \(q\in \mathbb{N}\). Then, by \((B)\), together with (2.6), we obtain

It follows that \(\{ \eta _{n} \} \) is a Cauchy sequence in a  -orbitally complete b-metric space. Therefore, we can find
-orbitally complete b-metric space. Therefore, we can find  such that
such that  .
.
We claim that ϖ is a fixed point of the mapping  under of any hypothesis, \((\mathit{iii})_{1}\) or \((\mathit{iii})_{2}\).
under of any hypothesis, \((\mathit{iii})_{1}\) or \((\mathit{iii})_{2}\).
Indeed,

Moreover,

If  is m-continuous, then
is m-continuous, then  , and by (2.7) it follows that
, and by (2.7) it follows that  .
.
If  is assumed to be orbitally continuous on
is assumed to be orbitally continuous on  , then
, then

Therefore,  . □
. □
Example
Let  and
and  be the b-metric defined as
be the b-metric defined as  for all
for all  . Let the mapping
. Let the mapping  be defined by
be defined by

and a function  , where
, where

Let also the comparison function \(\phi :[0,\infty )\rightarrow [0,\infty )\), \(\phi (t)=t/3\), and we choose  ,
,  ,
,  . Thus, we can easily observe that assumptions (i) and (ii) are satisfied, and since
. Thus, we can easily observe that assumptions (i) and (ii) are satisfied, and since  is continuous, assumption (iv) is also verified.
is continuous, assumption (iv) is also verified.
Case \((i.)\) For  , we have
, we have  , so inequality (2.1) holds.
, so inequality (2.1) holds.
Case \((\mathit{ii}.)\) For  and \(\omega =2\), we have
and \(\omega =2\), we have  and
and  . Thus, (2.1) holds.
. Thus, (2.1) holds.
Case \((\mathit{iii}.) \) For  and \(\omega =3\), we have
and \(\omega =3\), we have  ⇒
⇒

Case \((\mathit{iv}.) \) For  and \(\omega =9\), we have
and \(\omega =9\), we have  ⇒
⇒

All other cases are of no interest because  and (2.1) is satisfied.
and (2.1) is satisfied.
Therefore, the mapping  is an
is an  -admissible interpolative contraction. On the other hand, since
-admissible interpolative contraction. On the other hand, since  is continuous and
is continuous and  is α-orbital continuous, by Theorem 2.2 we get that there exists a fixed point of the mapping
is α-orbital continuous, by Theorem 2.2 we get that there exists a fixed point of the mapping  ; that is,
; that is,  .
.
Theorem 2.3
Let  be a complete b-metric space and
be a complete b-metric space and  be an
be an  -admissible interpolative contraction such that
-admissible interpolative contraction such that
- \((i)\):
-
 is α-orbital admissible;
is α-orbital admissible; - \((\mathit{ii})\):
-
there exists
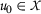 such that
such that 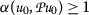 ;
; - \((\mathit{iii}_{1})\):
-
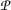 is m-continuous for \(m\geq 1\), or
is m-continuous for \(m\geq 1\), or - \((\mathit{iii}_{2})\):
-
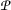 is orbitally continuous.
is orbitally continuous.
Then  possesses a fixed point
possesses a fixed point  .
.
Proof
As in the previous proof, for  , we build the sequence \(\{ \eta _{n} \} \), where
, we build the sequence \(\{ \eta _{n} \} \), where  and
and  for any \(n\in \mathbb{N}\). Since \(\eta _{n-1}\neq \eta _{n}\) for any \(n\in \mathbb{N}\cup {0}\), taking into account that the mapping
for any \(n\in \mathbb{N}\). Since \(\eta _{n-1}\neq \eta _{n}\) for any \(n\in \mathbb{N}\cup {0}\), taking into account that the mapping  is supposed to be
is supposed to be  -admissible interpolative contraction, we have
-admissible interpolative contraction, we have

where

Therefore, since by assumption \((i)\) it follows that \(\alpha (\eta _{n-1},\eta _{n})\geq 1\) for all \(n\in \mathbb{N}\), we have

(Here, we used the property \((\phi 1)\) of the function ϕ.)
Thus,

and then  for any \(n\in \mathbb{N}\). Furthermore, by (2.8) and keeping in mind \((\phi 2)\), we obtain
for any \(n\in \mathbb{N}\). Furthermore, by (2.8) and keeping in mind \((\phi 2)\), we obtain

and following the same steps as in the proof of Theorem 2.2, we can easily find that the sequence \(\{ \eta _{n} \} \) is Cauchy. Moreover, since  is supposed to be
is supposed to be  -orbitally complete, we can find a point
-orbitally complete, we can find a point  such that
such that  . Assuming that
. Assuming that  is m-continuous, we have
is m-continuous, we have

and assuming that  is orbitally continuous, we get
is orbitally continuous, we get

that is, ϖ is a fixed point of  . □
. □
In case we replace the continuity condition of the mapping with the continuity of the b-metric  , we get the following results.
, we get the following results.
Theorem 2.4
Let  be a complete, α-regular b-metric space, where the b-metric
be a complete, α-regular b-metric space, where the b-metric  is continuous, and
is continuous, and  is such that
is such that

where \(\phi \in \Theta \) and  , for \(l=1,2\) are given by (2.2) and (2.3). If
, for \(l=1,2\) are given by (2.2) and (2.3). If
- \((i)\):
-
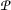 is α-orbital admissible;
is α-orbital admissible; - \((\mathit{ii})\):
-
there exists
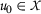 such that
such that  .
.
Then  possesses a fixed point
possesses a fixed point  , and the sequence
, and the sequence  converges to this point ϖ.
converges to this point ϖ.
Proof
From the proof of Theorem 2.2 we know that the sequence \(\{ \eta _{n} \} \), where  converges to a point
converges to a point  , and we claim that ϖ is a fixed point of the mapping
, and we claim that ϖ is a fixed point of the mapping  . For this purpose, we claim that
. For this purpose, we claim that

or

Indeed, supposing the contrary

we get that

This is a contradiction, and then (2.10) or (2.11) holds. Under the regularity assumption of the space  , we have that \(\alpha (\eta _{n},\varpi )\geq 1\) for any \(n\in \mathbb{N}\).
, we have that \(\alpha (\eta _{n},\varpi )\geq 1\) for any \(n\in \mathbb{N}\).
Case 1. (\(l=1\))
We can distinguish the following two situations:
-
(i)
 .
.Letting \(n\rightarrow \infty \) in (2.12) respectively (2.13), we obtain
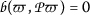 . Thus,
. Thus, 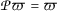 .
. -
(ii)
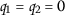 .
.In this case, when \(n\rightarrow \infty \), from (2.12), (2.13) and keeping in mind the continuity of b-metric
 , we get
, we get 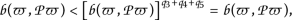
which is a contradiction.
Consequently,  , that is, ϖ is a fixed point of the mapping
, that is, ϖ is a fixed point of the mapping  .
.
Case 2. (\(l=2\))
We can distinguish the following two situations:
-
(i)
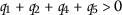 .
.Letting \(n\rightarrow \infty \) in (2.14), respectively (2.15), we obtain
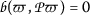 . Thus,
. Thus, 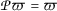 .
. -
(ii)
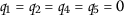 .
.In this case, when \(n\rightarrow \infty \), from (2.14) and (2.15), we get
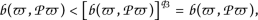
which is a contradiction.
Consequently,  , that is, ϖ is a fixed point of the mapping
, that is, ϖ is a fixed point of the mapping  . □
. □
Example
Let  and
and  be a b-metric space (\(s=2\)), defined by
be a b-metric space (\(s=2\)), defined by

Let  be a self-mapping on
be a self-mapping on  , with
, with  and
and  . Taking
. Taking  ,
,  for all
for all  , \(\phi (t)=t/2\) and the constants
, \(\phi (t)=t/2\) and the constants  for \(i\in \{ 1,2,3,4,5 \} \), we have
for \(i\in \{ 1,2,3,4,5 \} \), we have

Thus, by Theorem 2.4, the mapping  has (at least) a fixed point.
has (at least) a fixed point.
3 Consequences
Corollary 3.1
Let  be a complete b-metric space and
be a complete b-metric space and  be a mapping such that
be a mapping such that

for any  , where
, where  , \(l=1,2\), are defined by (2.2) and (2.3) and \(\phi \in \Theta \). Then
, \(l=1,2\), are defined by (2.2) and (2.3) and \(\phi \in \Theta \). Then  possesses a fixed point
possesses a fixed point  provided that
provided that
- \((i)\):
-
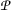 is α-orbital admissible;
is α-orbital admissible; - \((\mathit{ii})\):
-
there exists
 such that
such that 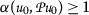 ;
; - \((\mathit{iii}_{1})\):
-
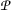 is m-continuous for \(m\geq 1\), or
is m-continuous for \(m\geq 1\), or - \((\mathit{iii}_{2})\):
-
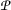 is orbitally continuous.
is orbitally continuous.
Corollary 3.2
Let  be a complete b-metric space and
be a complete b-metric space and  be a mapping such that
be a mapping such that

for any  , where
, where  , \(l=1,2\), are defined by (2.2) and (2.3). Then
, \(l=1,2\), are defined by (2.2) and (2.3). Then  possesses a fixed point
possesses a fixed point  , provided that either
, provided that either  is m-continuous for \(m\geq 1\) or
is m-continuous for \(m\geq 1\) or  is orbitally continuous.
is orbitally continuous.
Proof
Put  in Theorem 2.2, respectively 2.3. □
in Theorem 2.2, respectively 2.3. □
Corollary 3.3
Let  be a complete b-metric space and
be a complete b-metric space and  be a mapping such that there exists \(\kappa \in [0,1)\) such that
be a mapping such that there exists \(\kappa \in [0,1)\) such that

for any  , where
, where  , \(l=1,2\), are defined by (2.2) and (2.3). Then
, \(l=1,2\), are defined by (2.2) and (2.3). Then  possesses a fixed point
possesses a fixed point  , provided that either
, provided that either  is m-continuous for \(m\geq 1\), or
is m-continuous for \(m\geq 1\), or  is orbitally continuous.
is orbitally continuous.
Proof
Put \(\phi (t)=\kappa \cdot t\) in Corollary 3.2. □
Corollary 3.4
Let  be a complete b-metric space such that
be a complete b-metric space such that  is continuous. A mapping
is continuous. A mapping  has a fixed point in
has a fixed point in  provided that
provided that

where \(\phi \in \Theta \) and  , for \(l=1,2\) are given by (2.2) and (2.3).
, for \(l=1,2\) are given by (2.2) and (2.3).
Proof
Put  in Theorem 2.4. □
in Theorem 2.4. □
Corollary 3.5
Let  be a complete b-metric space such that
be a complete b-metric space such that  is continuous. A mapping
is continuous. A mapping  has a fixed point in
has a fixed point in  provided that there exists \(\kappa \in [0,1)\) such that
provided that there exists \(\kappa \in [0,1)\) such that

where  for \(l=1,2\) are given by (2.2) and (2.3).
for \(l=1,2\) are given by (2.2) and (2.3).
Proof
Put \(\phi (t)=\kappa \cdot t\) in Corollary 3.4. □
Availability of data and materials
No data was generated or used during the study; this paper was not about data.
References
Caccioppoli, R.: Una teorema generale sull’esistenza di elementi uniti in una transformazione funzionale. Rend. Accad. Naz. Lincei 11, 794–799 (1930)
Banach, S.: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 3, 133–181 (1922)
Bakhtin, I.A.: The contraction mapping principle in quasimetric spaces. Funct. Anal. Unianowsk Gos. Ped. Inst. 30, 26–37 (1989)
Czerwik, S.: Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1, 5–11 (1993)
Karapınar, E.: A short survey on the recent fixed point results on b-metric spaces. Constr. Math. Anal. 1(1), 15–44 (2018)
Alghamdi, M.A., Gulyaz-Ozyurt, S., Karapınar, E.: A note on extended Z-contraction. Mathematics 8, 195 (2020)
Afshari, H., Rezapour, Sh., Shahzad, N.: Absolute retract of the common fixed points set of two multifunctions. Topol. Methods Nonlinear Anal. 40, 429–436 (2012)
Aydi, H., Karapınar, E., Bota, M.F., Mitrovic, S.: A fixed point theorem for set-valued quasi-contractions in b-metric spaces. Fixed Point Theory Appl. 2012, 88 (2012)
Afshari, H., Aydi, H.: Existence and approximative fixed points for multifunctions. Asian-Eur. J. Math. 12, 1950022 (2019)
Aydi, H., Bota, M.F., Karapınar, E., Moradi, S.: A common fixed point for weak phi-contractions on b-metric spaces. Fixed Point Theory 13(2), 337–346 (2012)
Afshari, H., Alsulami, H.H., Karapınar, E.: On the extended multivalued Geraghty type contractions. J. Nonlinear Sci. Appl. 9, 46954706 (2016)
Afshari, H., Aydi, H., Karapınar, E.: On generalized α-ψ-Geraghty contractions on b-metric spaces. Georgian Math. J. 27, 9–21 (2020)
Pant, A., Pant, R.P.: Fixed points and continuity of contractive maps. Filomat 31(11), 3501–3506 (2017)
Popescu, O.: Some new fixed point theorems for α-Geraghty contractive type maps in metric spaces. Fixed Point Theory Appl. 2014, 190 (2014)
Karapınar, E.: Revisiting the Kannan type contractions via interpolation. Adv. Theory Nonlinear Anal. Appl. 2, 85–87 (2018)
Ćirić, Lj.: A generalization of Banach’s contraction principle. Proc. Am. Math. Soc. 45, 267–273 (1974)
Reich, S.: Some remarks concerning contraction mappings. Can. Math. Bull. 14, 121–124 (1971)
Rus, I.A.: Generalized Contractions and Applications. Cluj University Press, Clui-Napoca (2001)
Hardy, G.E., Rogers, T.D.: A generalization of a fixed point theorem of Reich. Can. Math. Bull. 16, 201–206 (1973)
Kannan, R.: Some results on fixed points. Bull. Calcutta Math. Soc. 60, 71–76 (1968)
Bianchini, R.M., Grandolfi, M.: Transformazioni di tipo contracttivo generalizzato in uno spazio metrico. Atti Accad. Naz. Lincei, VII. Ser. Rend. Cl. Sci. Fis. Mat. Natur. 45, 212–216 (1968)
Agarwal, R.P., Karapınar, E.: Interpolative Rus–Reich–Ciric type contractions via simulation functions. An. Ştiinţ. Univ. ‘Ovidius’ Constanţa, Ser. Mat. 27(3), 137–152 (2019)
Aydi, H., Chen, C.M., Karapınar, E.: Interpolative Ciric–Reich–Rus type contractions via the Branciari distance. Mathematics 7(1), 84 (2019)
Aydi, H., Karapınar, E., de Hierro, A.F.R.L.: ω-Interpolative Ciric–Reich–Rus-type contractions. Mathematics 7, 57 (2019)
Karapınar, E., Alqahtani, O., Aydi, H.: On interpolative Hardy–Rogers type contractions. Symmetry 11(1), 8 (2019)
Karapınar, E., Agarwal, R., Aydi, H.: Interpolative Reich–Rus–Ćirić type contractions on partial metric spaces. Mathematics 6, 256 (2018) https://doi.org/10.3390/math6110256
Acknowledgements
The author thanks the anonymous referees for their outstanding comments, suggestions, and ideas that helped improve this work.
Funding
This study did not receive funding.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fulga, A. On interpolative contractions that involve rational forms. Adv Differ Equ 2021, 448 (2021). https://doi.org/10.1186/s13662-021-03605-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03605-4
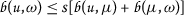 for every
for every 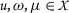 ,
, if
if 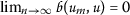 . The limit of a convergent sequence is unique;
. The limit of a convergent sequence is unique;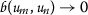 as
as 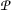 is α-orbital admissible;
is α-orbital admissible;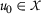 such that
such that 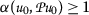 ;
;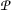 is m-continuous for
is m-continuous for 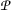 is orbitally continuous.
is orbitally continuous. is α-orbital admissible;
is α-orbital admissible;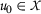 such that
such that 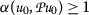 ;
;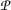 is m-continuous for
is m-continuous for 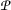 is orbitally continuous.
is orbitally continuous.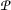 is α-orbital admissible;
is α-orbital admissible;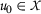 such that
such that  .
.

 .
.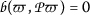 . Thus,
. Thus, 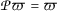 .
.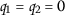 .
. , we get
, we get 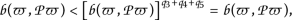


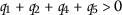 .
.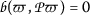 . Thus,
. Thus, 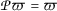 .
.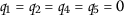 .
.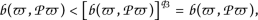
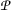 is α-orbital admissible;
is α-orbital admissible; such that
such that 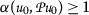 ;
;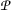 is m-continuous for
is m-continuous for 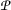 is orbitally continuous.
is orbitally continuous.