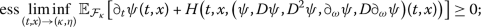- Research
- Open access
- Published:
Stochastic optimal control with random coefficients and associated stochastic Hamilton–Jacobi–Bellman equations
Advances in Continuous and Discrete Models volume 2022, Article number: 3 (2022)
Abstract
We consider the optimal control problem for stochastic differential equations (SDEs) with random coefficients under the recursive-type objective functional captured by the backward SDE (BSDE). Due to the random coefficients, the associated Hamilton–Jacobi–Bellman (HJB) equation is a class of second-order stochastic PDEs (SPDEs) driven by Brownian motion, which we call the stochastic HJB (SHJB) equation. In addition, as we adopt the recursive-type objective functional, the drift term of the SHJB equation depends on the second component of its solution. These two generalizations cause several technical intricacies, which do not appear in the existing literature. We prove the dynamic programming principle (DPP) for the value function, for which unlike the existing literature we have to use the backward semigroup associated with the recursive-type objective functional. By the DPP, we are able to show the continuity of the value function. Using the Itô–Kunita’s formula, we prove the verification theorem, which constitutes a sufficient condition for optimality and characterizes the value function, provided that the smooth (classical) solution of the SHJB equation exists. In general, the smooth solution of the SHJB equation may not exist. Hence, we study the existence and uniqueness of the solution to the SHJB equation under two different weak solution concepts. First, we show, under appropriate assumptions, the existence and uniqueness of the weak solution via the Sobolev space technique, which requires converting the SHJB equation to a class of backward stochastic evolution equations. The second result is obtained under the notion of viscosity solutions, which is an extension of the classical one to the case for SPDEs. Using the DPP and the estimates of BSDEs, we prove that the value function is the viscosity solution to the SHJB equation. For applications, we consider the linear-quadratic problem, the utility maximization problem, and the European option pricing problem. Specifically, different from the existing literature, each problem is formulated by the generalized recursive-type objective functional and is subject to random coefficients. By applying the theoretical results of this paper, we obtain the explicit optimal solution for each problem in terms of the solution of the corresponding SHJB equation.
1 Introduction
Let \((\Omega , \mathcal{F}, \mathbb{P},\{\mathcal{F}_{s}\}_{s \geq 0})\) be a complete filtered probability space, on which an r-dimensional standard Brownian motion, B, is defined, where \(\{\mathcal{F}_{s}\}_{s \geq 0}\) is a natural filtration generated by B augmented by all the \(\mathbb{P}\)-null sets in \(\mathcal{F}\). Let \(\mathbb{E}\) and \(\mathbb{E}_{\mathcal{F}_{s}}\) be the expectation and the conditional expectation with respect to \(\mathcal{F}_{s}\), respectively. For \(x,y \in \mathbb{R}^{n}\), \(x^{\top }\) denotes the transpose of x, \(\langle x,y \rangle \) is the inner product, and \(|x| := \langle x, x \rangle ^{1/2}\). Let \(\operatorname{Tr}(\cdot )\) be the trace operator. Let \(\mathbb{S}^{n}\) be the set of \(n \times n\) real symmetric matrices. Let \(s \in [0,T]\) and \(x \in \mathbb{R}^{n}\) be time and spatial variables, respectively.
In this paper, we consider the stochastic optimal control with random coefficients and the associated stochastic Hamilton–Jacobi–Bellman (SHJB) equation. Specifically, given the following forward–backward stochastic differential equation (FBSDE):
we formulate the stochastic control problem by defining the following value function:
Note that in (1) and (2), \(f: \Omega \times [0,T] \times \mathbb{R}^{n} \times U \rightarrow \mathbb{R}^{n}\), \(\sigma : \Omega \times [0,T] \times \mathbb{R}^{n} \times U \rightarrow \mathbb{R}^{n \times r}\), \(l: \Omega \times [0,T] \times \mathbb{R}^{n} \times U \times \mathbb{R} \times \mathbb{R}^{1 \times r} \rightarrow \mathbb{R}\), and \(m:\Omega \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) are random coefficients, where U is the control space that is a nonempty compact subset of \(\mathbb{R}^{m}\). We note that (2) is a class of recursive-type stochastic optimal control problems with random coefficients.
The first main objective of this paper is to obtain the dynamic programming principle (DPP) and the verification theorem for the value function in (2), where the latter constitutes a sufficient condition for optimality, provided that the associated SHJB equation (given below) admits a unique solution. The second main objective of this paper is to study the viscosity solution analysis of (2). That is, we show that the value function in (2) is the viscosity solution to the SHJB equation given by
where \(H:\Omega \times [0,T] \times \mathbb{R}^{n} \times \mathbb{R} \times \mathbb{R}^{n} \times \mathbb{S}^{n} \times \mathbb{R}^{1 \times r} \times \mathbb{R}^{r \times n} \rightarrow \mathbb{R}\) is the stochastic Hamiltonian defined by
We also obtain regularities of V in (2) with respect to both time and spatial variables. We should mention that by the coefficients in (1) and (2), the SHJB equation in (3) can be viewed as a class of second-order nonlinear stochastic partial differential equations (SPDEs) driven by Brownian motion. As in SPDEs, the two unknown components, \((V,q)\), define the solution of (3), which are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted stochastic processes.
The existence and uniqueness of (strong or weak) solutions to a class of SPDEs including SHJB equations has been regarded as an important research topic, since Peng initiated the problem in [1]. Specifically, [1] considered the stochastic optimal control problem with random coefficients, where the SHJB equation was first introduced. The SHJB equation in [1] is a special case of (3) in that l in (4) does not depend on y and \(q + \langle p,\sigma \rangle \) (equivalently, l in (1) does not depend on y and z). In fact, unlike [1], due to the recursive-type objective functional in (2), H, the drift term of the SHJB equation, depends on q, the second component of its solution. In [1], the existence and uniqueness of the weak solution was also shown via the Sobolev-space technique. Later, the approaches for the existence and uniqueness of (strong or weak) solutions for a class of SPDEs were established in the literature; see [2–9] and the references therein.
On the other hand, the existence and uniqueness of viscosity solutions for a class of SHJB equations had been a long-standing open problem [10]. Recently, this was solved in [11]. Note that the SHJB equation in [11] is identical with that of [1] and therefore is a special case of (3), for which l in (4) does not depend on y and \(q + \langle p,\sigma \rangle \) (equivalently, l in (1) does not depend on y and z). Hence, the problem formulation (see (2) and (3)) and the main results of this paper can be viewed as generalizations of those in [1, 11]. Below, we provide a detailed literature review and the summary of the main results of this paper.
As mentioned above, (2) is a class of recursive-type stochastic optimal control problems with random coefficients. Here, “recursive” means that the objective functional is also a dynamical system captured by the backward stochastic differential equation (BSDE) \((y_{s}^{t,a;u},z_{s}^{t,a;u})_{s \in [t,T]}\) in (1), where the optimization constraint is described by the forward SDE \((x_{s}^{t,a;u})_{s \in [t,T]}\) in (1). In fact, the motivation of studying recursive-type stochastic control problems is to consider the general dynamic structure of the objective functional. For example, the wealth process of investors in mathematical finance, the utility-maximization model in economics, and the (continuous-time) principal-agent problem in economics can be formulated using the framework of recursive-type BSDE objective functionals, which describe the general dynamic behavior of the investor (agent) [12–15]. Theoretically, the recursive-type stochastic control problem, which was first studied by [16], can be viewed as an extension of classical stochastic control problems (e.g., [17–20]) to the case when the objective functional itself has a dynamic structure.
There are various problem formulations, approaches, and results for recursive-type stochastic control problems. Specifically, [16] showed that the value function is the viscosity solution to the associated Hamilton–Jacobi–Bellman (HJB) equation. Note that the HJB equation in [16] can be regarded as a generalization of the classical HJB equations (e.g., [17–20]), where the dynamic structure of the recursive-type BSDE objective functional is embedded. Later, the results in [16] were generalized to the framework of two-player zero-sum differential games in [21], to the reflected recursive objective functional in [22], to the case with delay in [23], and to the risk-sensitive framework with the quadratic BSDE in [14]. Further, various stochastic maximum principles for recursive-type problems under different settings were established in [15, 24].
In stochastic optimal control, one can also formulate the problem with random coefficients as in (2). The purpose of allowing for random coefficients in stochastic control problems and their applications is to describe general modeling frameworks and to capture random parameter variations due to imprecisions, such as inaccurate modeling, environment changes, random disturbances, and the high sensitivity of dynamical systems [18, 25, 26]. From a theoretical perspective, stochastic control problems with random coefficients can be regarded as generalizations of classical stochastic control problems with deterministic coefficients (e.g., [17–20]). We note that, as discussed in [1, 11, 25–28], the approaches for solving stochastic control problems with random coefficients are different from those for the case with deterministic coefficients.
The first notable result of stochastic optimal control problems with random coefficients was obtained in [27] within the linear–quadratic (LQ) framework. The nonlinear stochastic control problem with random coefficients was studied in [1]. As stated above, unlike the case of deterministic coefficients, the HJB equation in [1] becomes the SHJB equation, which is the second-order SPDE driven by Brownian motion. The verification theorem, and the existence and uniqueness of the weak solution for the SHJB equation were also studied in [1]. Recently, the existence and uniqueness of the viscosity solution to the SHJB equation were studied in [11], where, as stated above, the SHJB equations in [11] and [1] are identical. Note that by the preceding discussion, the stochastic optimal control problem in [1, 11] is a special case of the problem in (2) (see Remark 2). Several different results for stochastic LQ control problems with random coefficients can be found in [25, 26, 28–30] and the references therein.
There are various applications of stochastic control with random coefficients and associated SHJB equations (or SPDEs), which can be studied using the approaches established in this paper. Specifically, optimizing of FitzHugh–Nagumo communication networks was considered in [31, 32], where their problems can be generalized to the recursive-type problem studied in this paper. Various mathematical finance problems with random coefficients were considered in [26, 30, 33], which can be studied in different aspects using the approach of this paper. We may also study a class of SPDEs including (3) for nonlinear filtering in partially observed stochastic control problems and differential games [34–38]. The reader is referred to [26, 30, 33, 34, 37–42] and the references therein for applications of stochastic control with random coefficients in diverse fields, such as mathematical finance, economics, engineering, analysis of SPDEs, and mean-field-type interacting-particle systems. Indeed, various applications of stochastic control problems with deterministic coefficients in mathematical finance, economics, science, and engineering (see [17–20] and the references therein) can be generalized to the recursive-type problem with random coefficients of this paper to model the general dynamic behavior of the objective functional and to capture random parameter variations due to imprecisions, such as inaccurate modeling, environment changes, random disturbances, and the high sensitivity of dynamical systems.
We should mention that the earlier results for recursive stochastic control problems mentioned above (see [14, 16, 21–23] and the references therein) considered the case with deterministic coefficients only. That is, their corresponding FBSDEs have deterministic coefficients. Hence, unlike (2) and (3), their value functions are deterministic, and their HJB equations are deterministic PDEs. Moreover, the existing literature on stochastic optimal control with random coefficients mentioned above (see [1, 11] and the references therein) did not consider the case of recursive-type BSDE objective functionals. Accordingly, in contrast to (3), the SHJB equation in [1, 11] cannot explain the dynamic structure of the objective functional, which is a special case of (3).Footnote 1 We stress that a complete analysis for the recursive-type stochastic control problem with random coefficients and its associated SHJB equation, formulated, respectively, in (2) and (3), has not been presented in the existing literature, which we address in this paper. The detailed statements of the comparison with the existing literature are given in Sect. 1.1.
We now summarize the main results of this paper:
-
(a)
We formulate the recursive-type stochastic optimal control problem with random coefficients given in (1) and (2).Footnote 2 We obtain the dynamic programming principle (DPP) for the value function in (2) (see Theorem 1), where, unlike the case with deterministic coefficients, (2) is a random field [1, 11]. The DPP in Theorem 1 is shown by using the backward semigroup associated with the recursive-type BSDE objective functional and the precise estimates of BSDEs including the comparison result. As a byproduct of the DPP, we are able to prove the continuity of the value function with respect to time and spatial variables (see Corollary 1);
-
(b)
We prove the verification theorem (see Theorem 2), which constitutes a sufficient condition for optimality and characterizes the value function in (2), provided that the smooth (classical) solution of the SHJB equation in (3) exists. To prove the verification theorem, we use the Itô–Kunita formula along with the precise estimates of BSDEs and the theory of linear BSDEs, which is different from the case without recursive-type BSDE objective functionals in [1, Sect. 3.2] (see a related discussion in Sect. 1.1);
-
(c)
As an application of the verification theorem, we study the general indefinite linear–quadratic (LQ) control problem with random coefficients, where the cost parameters need not be (positive-) definite matrices. In particular, we characterize the quadratic-type smooth solution of the SHJB equation in (3) for the LQ case. Then, by applying the verification theorem of Theorem 2, we obtain an explicit linear state-feedback optimal solution in terms of the solution of the corresponding SHJB equation (see Proposition 2). This result can be viewed as an extension of [25, 26, 43–45] to the problem with the recursive-type quadratic objective functional (see a related discussion in Sect. 1.1);
-
(d)
Note that in general, the smooth (classical) solution of the SHJB equation in (3) may not exist. Hence, we study the existence and uniqueness of the solution under two different weak-solution concepts, which leads to the characterization of the value function in (2). First, in the appendix, under the structural assumptions on the coefficients, we show the existence and uniqueness of the weak solution of the SHJB equation in (3) via the Sobolev-space technique and the evolution-type BSDE theory (see Theorem 6.1);
-
(e)
Secondly, we show that the value function in (2) is the viscosity solution to the SHJB equation in (3) (see Theorem 3). In particular, we provide the notion of viscosity solutions for (3) (see Definition 2), where its definition is an extension of the classical one (see [46]) to the case for SPDEs. Note that Definition 2 requires a class of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted stochastic processes that admits a Doob–Meyer-type decomposition (or weakly differentiable); see the definition of \(\mathscr{S}^{2}_{\mathcal{F}}\) in Definition 1. In fact, we modify the notion of viscosity solutions in [11], where the class of functions in \(\mathscr{S}^{2}_{\mathcal{F}}\) converts (3) into the one unknown component of the SPDE. Then, using the DPP and the precise estimates of BSDEs (including the continuity of the value function), we prove that the value function in (2) is a viscosity solution to the SHJB equation in (3) in the sense of Definition 2 (see Theorem 3), where its proof is different from that of [11, Theorem 4.2] due to the presence of the recursive-type objective functional (see a related discussion in Sect. 1.1). We also provide the uniqueness of the viscosity solution for (3) under additional parameter assumptions (including the superparabolic SPDE case) similar to [11] (see Theorems 4 and 5). We mention that the general uniqueness result of the viscosity solution for (3) remains an open problem, which we will address in the near future;
-
(f)
We consider two different applications of this paper arising in mathematical finance and economics. The first example is the utility-maximization problem (Sect. 4.1), whereas the second application is the European option-pricing problem (Sect. 4.2). Both problems consider the case of recursive-type BSDE objective functionals and are subject to random coefficients, which can be regarded as extensions of classical problems studied in the literature (e.g., [12, 13, 20, 47, 48]). We apply the theoretical results of this paper to obtain the explicit optimal solution for each problem in terms of the solution of the SHJB equation in (3). In fact, the optimal solution of the first problem (i.e., the utility-maximization problem) provides the optimal investment strategy (see Proposition 3), while that of the second example (i.e., the European option-pricing problem) characterizes the optimal portfolio strategy that achieves the corresponding contingent claim for the investor (see Proposition 4).
We discuss several potential applications of the results presented in this paper. As noted above, stochastic control problems can be applied to study various applications in finance, economics, science, and engineering. Then, these problems can be extended to the recursive-type problem with random coefficients studied in this paper, which allows capturing more practical situations, including the general dynamic behavior of the objective functional and the random parameter variations due to imprecisions.Footnote 3 In fact, two examples in the statement of (f) can be regarded as possible applications of the results of this paper in mathematical finance and economics. Another example would be the power-adjustment control problem in wireless communication networks studied in [49, 50]. This example can be studied using the formulation of this paper to describe more practical behavior such as the dynamic structure of optimal power adjustment and/or the unexpected parameter fluctuations. Finally, the results of this paper can be applied to study the optimization problem of FitzHugh–Nagumo neuron networks [31, 32].
The organization of the paper is as follows. Section 2 introduces the stochastic optimal control problem with random coefficients given in (1) and (2). We obtain the DPP for (2) and the verification theorem. We also consider the indefinite LQ problem in Sect. 2. In Sect. 3, we provide the notion of viscosity solutions and then show that the value function in (2) is the corresponding viscosity solution of (3). The uniqueness of the viscosity solution for (3) is also shown in Sect. 3. In Sect. 4, two different applications of this paper in mathematical finance including the application of the SHJB equation in (3) are considered. We conclude the paper in Sect. 5. In the appendix, we show the existence and uniqueness of the weak solution to (3).
1.1 Comparison of the paper with the existing literature
This paper extends the results in the existing literature in several different directions. Below, we provide the detailed comparisons (the statements given earlier in (a)–(f)) with the existing literature.
The statement in (a) generalizes the results of [11, Theorem 3.4] to the case of recursive-type BSDE objective functionals. In particular, unlike [11, Theorem 3.4], to prove the DPP (see Theorem 1), we have to use the semigroup property of the auxiliary BSDE associated with the recursive-type objective functional (see (9)) and the precise estimates of BSDEs including the comparison result. Furthermore, the proof for the continuity of the value function in our paper (see Corollary 1) requires the application of the DPP in Theorem 1 and the precise estimates of BSDEs, which must be different from [11, Proposition 3.3].
Regarding the statement in (b), the verification theorem of this paper (see Theorem 2) extends [1, Sect. 3.2] to the case of recursive-type BSDE objective functionals with random coefficients. We note that the proof for Theorem 2 is necessarily different from that of [1, Sect. 3.2]. Specifically, unlike [1, Sect. 3.2], to cope with the stochastic nature of the SHJB equation in (3) with the presence of generalized components y and \(q + \langle p,\sigma \rangle \) in l of (4), we have to use the Itô–Kunita’s formula and the precise estimates of BSDEs, including the linear BSDE theory and the comparison result, to obtain the desired optimality condition. In addition, as for the statement in (d), in the appendix, we show the existence and uniqueness of the weak solution to the SHJB equation in (3) via the Sobolev-space technique and the evolution-type BSDE theory (see Theorem 6.1), which can be viewed as an extension of [1, Sect. 4] to the case of recursive-type objective functionals.
As seen from the statement in (c), we generalize the earlier LQ results in [25, 26, 43–45] to the problem of the recursive-type quadratic objective functional with random coefficients. In particular, in contrast to [25, 26, 43–45], due to the dependence of l in (4) on y and \(q + \langle p,\sigma \rangle \), the standard completion of squares method cannot be applied, and we have to solve the complex SHJB equation in (3) for the LQ case to characterize the corresponding optimal solution via the verification theorem (see Proposition 2). Note that when l in (4) does not depend on y and \(q + \langle p,\sigma \rangle \), Proposition 2 degenerates to [26, Theorem 1] and [44, Theorem 5.1], in which case we can simply use the completion of squares technique to obtain the optimal solution instead of solving the SHJB equation (see [26, Theorem 1]).
As for the statement in (e), Theorem 3 shows that the value function in (2) is the viscosity solution to the SHJB equation in (3) in the sense of Definition 2, which is an extension of [11, Theorem 4.2] to the case for recursive-type BSDE objective functionals with random coefficients. We mention that the proof for Theorem 3 is completely different from that of [11, Theorem 4.2] due to the presence of generalized components y and \(q + \langle p,\sigma \rangle \) in l of (4). Specifically, in contrast to [11, Theorem 4.2], in the proof of Theorem 3, the auxiliary BSDE in terms of the value function has to be constructed, which together with the Itô–Kunita formula, the DPP, and the precise estimates of BSDEs (including the linear BSDE theory and the continuity of the value function) shows that the value function in (2) is the viscosity solution to the SHJB equation in (3). We mention that such an extended analysis, including the construction of the auxiliary BSDE and the application of the linear BSDE theory, was not presented [11, Theorem 4.2].
Regarding the statement in (f), we provide different aspects of the classical utility maximization and European option-pricing problems studied in the literature (e.g., [12, 13, 20, 47, 48]). In particular, these two applications (see Propositions 3 and 4) consider the case of recursive-type BSDE objective functionals with random coefficients, which have not been studied in the existing literature.
1.2 Notation
Let \(\mathbb{X}\) be a Banach space equipped with norm \(\|\cdot \|_{\mathbb{X}}\). For \(s \in [0,T]\) and \(p \geq 1\), let \(L^{p}(\Omega ,\mathcal{F}_{s};\mathbb{X})\) be the space of \(\mathcal{F}_{s}\)-measurable \(\mathbb{X}\)-valued random variables with \(\mathbb{E}[\|\cdot \|_{\mathbb{X}}^{p}] < \infty \). Let \(\mathcal{C}_{\mathcal{F}}^{p}(\mathbb{X})\) be the set of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \(\mathbb{X}\)-valued continuous random processes with \(\|\cdot \|_{\mathcal{C}_{\mathcal{F}}^{p}(\mathbb{X})} := \| \sup_{s \in [0,T]} \|\cdot \|_{\mathbb{X}} \|_{L^{p}(\Omega ,\mathcal{F}; \mathbb{X})} < \infty \). We denote by \(\mathcal{L}_{\mathcal{F}}^{p}(\mathbb{X})\) the set of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \(\mathbb{X}\)-valued random processes with \(\|\cdot \|_{\mathcal{L}_{\mathcal{F}}^{p}(\mathbb{X})} := \| (\int _{0}^{T} \|\cdot \|_{\mathbb{X}}^{p} \,\mathrm{d}s )^{\frac{1}{p}} \|_{L^{p}(\Omega , \mathcal{F};\mathbb{X})} < \infty \). When \(p=2\) and \(\mathbb{X} = \mathbb{R}^{n}\), we have \(\|\cdot \|_{\mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R}^{n})} = \mathbb{E}[\sup_{s \in [0,T]} |\cdot |^{2}]\) and \(\|\cdot \|_{\mathcal{L}_{\mathcal{F}}^{2}(\mathbb{R}^{n})} = \mathbb{E}[\int _{0}^{T} |\cdot |^{2} \,\mathrm{d}s]\). Note that \(\mathcal{L}_{\mathcal{F}}^{\infty }(\mathbb{X}) = \mathcal{C}_{ \mathcal{F}}^{\infty }(\mathbb{X})\) is the set of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \(\mathbb{X}\)-valued random processes, which are essentially bounded. Note also that both \((\mathcal{L}_{\mathcal{F}}^{p}(\mathbb{X}), \|\cdot \|_{\mathcal{L}_{ \mathcal{F}}^{p}(\mathbb{X})})\) and \((\mathcal{C}_{\mathcal{F}}^{p}(\mathbb{X}), \|\cdot \|_{\mathcal{C}_{ \mathcal{F}}^{p}(\mathbb{X})})\) are Banach spaces [18].
Let \(C^{k}(\mathbb{R}^{n};\mathbb{R}^{m})\), \(k \geq 0\), be the set of \(\mathbb{R}^{m}\)-valued continuous functions on \(\mathbb{R}^{n}\) such that \(f \in C^{k}(\mathbb{R}^{n};\mathbb{R}^{m})\) is up to kth-order differentiable in \(\mathbb{R}^{n}\), which are continuous and bounded. This is a Banach space with the supremum norm [51]. We let \(C^{k}(\mathbb{R}^{n}) := C^{k}(\mathbb{R}^{n};\mathbb{R})\). Then, \(f \in \mathcal{C}_{\mathcal{F}}^{2}(C^{2}(\mathbb{R}^{n}))\) is a stochastic process such that for each \(s \in [0,T]\), \((f,D f, D^{2} f)\) exist and are continuous and bounded on \(\mathbb{R}^{n}\), and for each \(x \in \mathbb{R}^{n}\) \((f,D f, D^{2} f)\) are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \((\mathbb{R},\mathbb{R}^{n},\mathbb{S}^{n})\)-valued continuous stochastic processes with \(\|\cdot \|_{\mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R})} < \infty \). Note that \(\mathcal{L}_{\mathcal{F}}^{2}(C^{2}(\mathbb{R}^{n}))\) and \(\mathcal{L}_{\mathcal{F}}^{\infty }(C^{2}(\mathbb{R}^{n}))\) can be defined similarly. Let \((W^{k,q}(\mathbb{R}^{n}),\|\cdot \|_{k,q})\) be the usual Sobolev space for real-valued functions on \(\mathbb{R}^{n}\) (in the sense of weak derivatives in \(\mathbb{R}^{n}\)) [51]. Let \(H^{k} := W^{k,2}\) with \(\|\cdot \|_{k} := \|\cdot \|_{k,2}\). \((W^{k,q}(\mathbb{R}^{n}),\|\cdot \|_{k,q})\) is a Banach space and \((H^{k},\|\cdot \|_{k})\) is a Hilbert space [51]. Then, \(\mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))\) is the set of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \(H^{k}(\mathbb{R}^{n})\)-valued random processes with norm \(\|\cdot \|_{\mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))} = \mathbb{E}[\int _{0}^{T} \|\cdot \|_{k}^{2} \,\mathrm{d}s]\). That is, for \(f \in \mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))\), the weak derivatives of f up to kth-order are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted stochastic processes, which belong to \(\mathcal{L}_{\mathcal{F}}^{2}\).
In various places, an exact value of constant C can vary from line to line, which depends on (H.1) and (H.2) (and other parameters) below but independent of a specific choice of control. Moreover, in our paper, the essential supremum (denoted by ess sup) and the essential infimum (denoted by ess inf) are taken with respect to an indexed family of random variables; see the precise idea in [52, Appendix A] and [20, Chap. 10.6].Footnote 4
2 Stochastic optimal control with random coefficients
In this section, we consider the stochastic optimal control problem with random coefficients. The objective functional is the recursive type captured by the backward stochastic differential equation (BSDE) with random coefficients. We prove the DPP, the continuity property of the value function, and the verification theorem. We also consider the indefinite LQ problem as an application of the verification theorem.
2.1 Problem statement
The stochastic differential equation (SDE) is given by
where f and σ are the coefficients in (1) and (3). Note that \((x_{s}^{t,a;u})_{s \in [t,T]}\) is the \(\mathbb{R}^{n}\)-valued (forward) state process with the initial condition \(x_{t}^{t,a;u} = a\) and \((u_{s})_{s \in [t,T]}\) is the U-valued control process with the control space U. The space of admissible controls is defined by \(\mathcal{U}_{t,T} := \mathcal{L}^{2}_{\mathcal{F}}(U)\).
We introduce the backward SDE (BSDE) given by
where l and m are the coefficients in (1) and (3). The pair \((y_{s}^{t,a;u},z_{s}^{t,a;u})_{s \in [t,T]}\) is the \((\mathbb{R},\mathbb{R}^{1 \times r})\)-valued backward process. \(y_{T}^{t,a;u} = m(x_{T}^{t,a;u})\) is the terminal condition that is \(\mathcal{F}_{T}\)-measurable. As stated in (2) and (3), \(f: \Omega \times [0,T] \times \mathbb{R}^{n} \times U \rightarrow \mathbb{R}^{n}\), \(\sigma : \Omega \times [0,T] \times \mathbb{R}^{n} \times U \rightarrow \mathbb{R}^{n \times r}\), \(l: \Omega \times [0,T] \times \mathbb{R}^{n} \times U \times \mathbb{R} \times \mathbb{R}^{1 \times r} \rightarrow \mathbb{R}\), and \(m:\Omega \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) are random coefficients of (5) and (6), where U is the control space that is a nonempty compact subset of \(\mathbb{R}^{m}\). Note that (5) and (6) constitute a forward–backward SDE with random coefficients, where the BSDE is coupled with the forward SDE in (4).
The assumptions for (5) and (6) are given as follows:
-
(H.1)
For \(\zeta = f,\sigma \), ζ is \(\mathbb{P} \times \mathcal{B}(\mathbb{R}^{n}) \times \mathcal{B}(U)\)-measurable, where \(\mathcal{B}(\cdot )\) is the Borel σ-algebra. For almost all \(\omega \in \Omega \), ζ is (uniformly) continuous in \((s,u) \in [0,T] \times U\) and Lipschitz continuous in \(x \in \mathbb{R}^{n}\) with the Lipschitz constant L.
-
(H.2)
l and m are \(\mathbb{P} \times \mathcal{B}(\mathbb{R}^{n}) \times \mathcal{B}(U) \times \mathcal{B}(\mathbb{R}) \times \mathcal{B}(\mathbb{R}^{1 \times r}) \) and \(\mathbb{P} \times \mathcal{B}(\mathbb{R}^{n})\) measurable, respectively. For almost all \(\omega \in \Omega \), l is (uniformly) continuous in \((s,u) \in [0,T] \times U\) and Lipschitz continuous in \((x,y,z) \in \mathbb{R}^{n} \times \mathbb{R} \times \mathbb{R}^{1 \times r}\) with the Lipschitz constant L. For almost all \(\omega \in \Omega \), m is Lipschitz continuous in \(x \in \mathbb{R}^{n}\) with L.
Remark 1
We should mention that in (5) and (6), the coefficients f, σ, l and m are allowed to be random, which are just measurable with respect to \(\omega \in \Omega \). In particular, unlike the path-dependent stochastic control problems and differential games in [53–59], there are no specific assumptions for the coefficients with respect to \(\omega \in \Omega \) and there is no specified topology on Ω.
We have the following lemma. The proof can be found in [18, Chaps. 1 and 7], [13, Chaps. 3, 4 and 8], [20].
Lemma 1
Assume that (H.1) and (H.2) hold. Then, for \(t \in [0,T]\), \(s,l \in [t,T]\), \(l \leq s\), \(u \in \mathcal{U}_{t,T}\), and \(a,a^{\prime }\in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\), the following results hold:
-
(i)
(5) admits a unique (strong) solution in \(\mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R}^{n})\). Moreover, for \(p \geq 1\), \((x_{s}^{t,a;u})_{s \in [l,T]} = (x_{s}^{t,x_{l}^{t,a;u};u})_{s \in [l,T]}\) and there exists a constant \(C>0\), dependent on L, T and p, such that (\(\mathbb{P}\)-almost surely (a.s.))
$$\begin{aligned} &\mathbb{E}_{\mathcal{F}_{t}} \Bigl[\max_{s \in [t,T]} \bigl\vert x_{s}^{t,a;u} \bigr\vert ^{p} \Bigr] \leq C \bigl(1+ \vert a \vert ^{p} \bigr), \\ &\mathbb{E}_{\mathcal{F}_{t}} \bigl[ \bigl\vert x_{s}^{t,a;u} - x_{l}^{t,a;u} \bigr\vert ^{p} \bigr]\leq C \bigl(1+ \vert a \vert ^{p} \bigr) (s-l)^{\frac{p}{2}}, \\ &\mathbb{E}_{\mathcal{F}_{t}} \Bigl[\max_{s \in [t,T]} \bigl\vert x_{s}^{t,a;u} - x_{s}^{t,a^{\prime };u} \bigr\vert ^{p} \Bigr]\leq C \bigl\vert a-a^{\prime } \bigr\vert ^{p}; \end{aligned}$$ -
(ii)
(6) admits a unique solution \((y_{s}^{t,a;u},z_{s}^{t,a;u})_{s \in [t,T]} \in \mathcal{C}_{ \mathcal{F}}^{2}(\mathbb{R}) \times \mathcal{L}_{\mathcal{F}}^{2}( \mathbb{R}^{1 \times r})\). Furthermore, for \(p \geq 2\), there exists a constant \(C>0\), dependent on L, p and T, such that (\(\mathbb{P}\)-a.s.)
$$\begin{aligned}& \mathbb{E}_{\mathcal{F}_{t}} \biggl[\max_{s \in [t,T]} \bigl\vert y_{s}^{t,a;u} \bigr\vert ^{p} + \biggl( \int _{t}^{T} \bigl\vert z_{s}^{t,a;u} \bigr\vert ^{2} \,\mathrm{d}s \biggr)^{\frac{p}{2}} \biggr] \leq C \bigl(1 + \vert a \vert ^{p} \bigr), \\& \mathbb{E}_{\mathcal{F}_{t}} \bigl[ \bigl\vert y_{s}^{t,a;u} - y_{t}^{t,a;u} \bigr\vert ^{p} \bigr] \leq C \bigl(1+ \vert a \vert ^{p} \bigr) (t-s)^{\frac{p}{2}}, \\& \mathbb{E}_{\mathcal{F}_{t}} \Bigl[\max_{s \in [t,T]} \bigl\vert y_{s}^{t,a;u} - y_{s}^{t,a^{\prime };u} \bigr\vert ^{p} \Bigr] \leq C \bigl\vert a - a^{\prime } \bigr\vert ^{p}; \end{aligned}$$ -
(iii)
Suppose that \((\tilde{y}_{s}^{t,a;u}, \tilde{z}_{s}^{t,a;u})_{s \in [t,T]} \in \mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R}) \times \mathcal{L}_{ \mathcal{F}}^{2}(\mathbb{R}^{1 \times r})\) is the solution of (6), where \(\tilde{y}_{T}^{t,a;u} = m(x_{T}^{t,a;u}) + \epsilon \) and \(\epsilon > 0\). Then, there exists a constant \(C > 0\), dependent on L and T, such that \(\mathbb{E}_{\mathcal{F}_{t}}[\max_{s \in [t,T]} |y_{s}^{t,a;u} - \tilde{y}_{s}^{t,a;u}|^{2}] < C \epsilon \). Assume that \((\widehat{y}_{s}^{t,a;u}, \widehat{z}_{s}^{t,a;u})_{s \in [t,T]} \in \mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R}) \times \mathcal{L}_{ \mathcal{F}}^{2}(\mathbb{R}^{1 \times r})\) is the solution of (6) with l̂ and m̂, where \(l \geq \widehat{l}\) and \(m \geq \widehat{m}\), \(\mathbb{P}\)-a.s. Then, \(y_{s}^{t,a;u} \geq \widehat{y}_{s}^{t,a;u}\) for \(s \in [t,T]\), \(\mathbb{P}\)-a.s.
The objective functional is a recursive type given by
Then, the stochastic optimal control problem considered in this paper can be stated as follows:
Remark 2
When l in (6) does not depend on y and z, the objective functional J in (7) can be simplified as follows:
This is a special case of (P), which was considered in [1, 11].
For \(t \in [0,T]\) and \(a \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\), the value function of (P) is defined by
Note that from Lemma 1, (P) is well posed; hence, (8) is the well-defined value function. If the coefficients in (5) and (6) are not dependent on \(\omega \in \Omega \), then the problem above corresponds to stochastic optimal control with deterministic coefficients, which has been studied in various aspects in the literature; see [17, 18, 20] and the references therein. Unlike the case of deterministic coefficients, the value function in (8) is a random field.
Remark 3
We mention that the purpose of choosing stochastic optimal controller design is to broaden its potential applications. Specifically, there are various applications of stochastic control problems in finance, economics, science, and engineering. Then, these applications can be studied in different aspects using the approaches of this paper, which allows capturing more practical situations including the general dynamic behavior of the objective functional and the random parameter variations due to imprecisions (see the detailed discussion in Sect. 1).
2.2 Dynamic programming principle and verification theorem
This subsection provides the continuity property of (8). We show that (8) satisfies the DPP, which is the recursive-type value iteration algorithm to solve (P). Then, we prove the verification theorem for (P).
We first state the following result due to Lemma 1:
Lemma 2
Assume that (H.1) and (H.2) hold. Then, there exists a constant \(C>0\) such that for \(a,a^{\prime }\in \mathbb{R}^{n}\),
The backward semigroup operator associated with the BSDE is defined as follows: for \(t,t+\tau \in [0,T]\) with \(t < t+\tau \),
where \((\bar{y}_{s}^{t,a;u},\bar{z}_{s}^{t,a;u})_{s \in [t,t+\tau ]}\) is the solution of the following BSDE on \([t,t+\tau ]\):
Here, \(b \in L^{2}(\Omega ,\mathcal{F}_{t+\tau };\mathbb{R})\). Obviously, when \(b=y_{t+\tau }^{t,a;u}\) (note that \(y_{t+\tau }^{t,a;u} \in L^{2}(\Omega ,\mathcal{F}_{t+\tau };\mathbb{R})\)), we have \(y_{t}^{t,a;u} = \bar{y}_{t}^{t,a;u} = \Phi _{t,t+\tau }^{t,a;u}[y_{t+ \tau }^{t,a;u}]\), \(\mathbb{P}\)-a.s.
Remark 4
By (9) and (i) of Lemma 1, the objective functional in (7) can be rewritten as follows:
We now state the DPP for (P).
Theorem 1
Suppose that (H.1) and (H.2) hold. Then, the value function in (8) satisfies the following dynamic programming principle (DPP): for \(t,t+\tau \in [0,T]\) with \(t < t+\tau \) and \(a \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\),
Proof
Note that in view of Lemma 1, the FBSDE in (5) and (6) admit a unique solution of \((x_{s}^{t,a;u}, y_{s}^{t,a;u},z_{s}^{t,a;u})_{s \in [t,T]} \in \mathcal{C}_{\mathcal{F}}^{2}(\mathbb{R}^{n}) \times \mathcal{C}_{ \mathcal{F}}^{2}(\mathbb{R}) \times \mathcal{L}_{\mathcal{F}}^{2}( \mathbb{R}^{1 \times r})\).
Let
We show that \(V^{\prime }(t,a) \leq V(t,a)\) and \(V^{\prime }(t,a) \geq V(t,a)\).
First, note from (7) and Remark 4 that
where the inequality follows from (8) and (iii) of Lemma 1. This implies that \(V(t,a) \geq V^{\prime }(t,a)\).
We now prove \(V(t,a) \leq V^{\prime }(t,a)\). By Lemma 2 and (ii) of Lemma 1, for each \(\epsilon > 0\), there exists \(\delta > 0\) such that whenever \(|x - \hat{x}| < \delta \), it holds that for all \(u \in \mathcal{U}_{t+\tau ,T}\),
Denote \(\{D_{j}\}_{j \geq 1}\) by the (disjoint) Borel partition of \(\mathbb{R}^{n}\) having the diameter of δ, i.e., \(\operatorname{diam}(D_{j}) < \delta \). This is equivalently saying that \(D_{j}\) is Borel measurable, i.e., \(D_{j} \in \mathcal{B}(\mathbb{R}^{n})\), with \(\bigcup_{j \geq 1} D_{j} = \mathbb{R}^{n}\) and \(D_{j} \cap D_{l} = \phi \) for \(j \neq l\). By definition, for \(x,\hat{x} \in D_{j}\), we have \(|x-\hat{x}|< \delta \). For each j, choose \(x^{(j)} \in D_{j}\). Then, by the measurable selection theorem in [11, Theorem A.1] (see also [60, 61]), there exists \(u^{(j)} \in \mathcal{U}_{t+\tau ,T}\) such that \(J(t+\tau ,x^{(j)};u^{(j)}) \leq V(t+\tau ,x^{(j)}) +\epsilon \). Hence, by (10), for any \(x \in D_{j}\),
For any \(u^{\prime \prime } \in \mathcal{U}_{t,t+\tau }\), we define

where  is the indicator function. Clearly, \(\tilde{u} \in \mathcal{U}_{t,T}\). Let
is the indicator function. Clearly, \(\tilde{u} \in \mathcal{U}_{t,T}\). Let  . Then, by Remark 4,
. Then, by Remark 4,
where the second inequality is due to (11) and (iii) of Lemma 1. Then, (12) and the definition of \(V^{\prime }\), together with the arbitrariness of ϵ, imply that (after taking the essential infimum) we can obtain \(V(t,a) \leq V^{\prime }(t,a)\). This shows that \(V(t,a) = V^{\prime }(t,a)\); thus completing the proof. □
We now state the continuity property of (8) in \(t \in [0,T]\).
Proposition 1
Suppose that (H.1) and (H.2) hold. Then, (8) is continuous in \(t \in [0,T]\). Specifically, there exists a constant \(C>0\) such that for \(a \in \mathbb{R}^{n}\) and \(t,t+\tau \in [0,T]\) with \(t < t+\tau \),
Proof
It is necessary to prove that
Below, it is shown that \(V(t,a) - V(t+\tau ,a) \leq C (1+|a|)\tau ^{\frac{1}{2}}\).
In view of Theorem 1, for each \(\epsilon > 0\), there exists \(u^{\prime }\in \mathcal{U}_{t,t+\tau }\) such that
This implies that
where
From (i) of Lemma 1, Lemma 2, and Jensen’s inequality, (\(\mathbb{P}\)-a.s.)
Moreover, from the definition of Φ and the terminal condition of Φ in \(I^{(2)}\), we use Lemma 1 and (H.2) to obtain
Note that (13) and (14) lead to
Hence, the arbitrariness of ϵ implies \(V(t,a) - V(t+\tau ,a) \leq C(1+|a|) \tau ^{1/2}\), \(\mathbb{P}\)-a.s. The other inequality can be proven in a similar way. This completes the proof. □
From Lemma 2 and Proposition 1, the following result holds:
Corollary 1
Assume that (H.1) and (H.2) hold. Then, the value function in (8) is continuous on \([0,T] \times \mathbb{R}^{n}\). Specifically, for \(a,a^{\prime }\in \mathbb{R}^{n}\) and \(t,t+\tau \in [0,T]\) with \(t < t+\tau \),
We now state the verification theorem for (P).
Theorem 2
Assume that (H.1) and (H.2) hold. Suppose that the pair \((V,q) \in \mathcal{L}^{\infty }_{\mathcal{F}}(C^{2}(\mathbb{R}^{n})) \times \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}^{n};\mathbb{R}^{1 \times r}))\) is the solution to the SHJB equation in (3). Then, for \(t \in [0,T]\), \(x \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\) and \(u \in \mathcal{U}_{t,T}\), \(V(t,x) \leq J(t,x;u)\), \(\mathbb{P}\)-.a.s. Furthermore, assume that \(\widehat{u}_{s} \in U\) with \(\widehat{u} := (\widehat{u}_{s})_{s \in [t,T]} \in \mathcal{U}_{t,T}\) is the minimizer of the Hamiltonian in (3) for \(s \in [t,T]\), \(\mathbb{P}\)-.a.s. Then, for \(t \in [0,T]\) and \(x \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\), we have \(V(t,x) =J(t,x;\widehat{u})\), \(\mathbb{P}\)-.a.s. and \(\widehat{u} \in \mathcal{U}_{t,T}\) is the corresponding optimal control.
Proof
Suppose that \((V,q) \in \mathcal{L}^{\infty }_{\mathcal{F}}(C^{2}(\mathbb{R}^{n})) \times \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}^{n};\mathbb{R}^{1 \times r}))\) is the solution of (3). Let \((x_{s}^{t,x;\widehat{u}})_{s \in [t,T]}\) be the state trajectory generated by \(\widehat{u} \in \mathcal{U}_{t,T}\) with \(x_{t}^{t,x;\widehat{u}} = x \in L^{2}(\Omega ,\mathcal{F}_{t}; \mathbb{R}^{n})\). Note that \(V(T,x_{T}^{t,x;\widehat{u}}) = m(x_{T}^{t,x;\widehat{u}})\) and \(V(t,x_{t}^{t,x;\widehat{u}}) = V(t,x)\), \(\mathbb{P}\)-a.s.
By using the Itô–Kunita formula [62] and the SHJB in (3), we have (\(\mathbb{P}\)-a.s.)
Let \((y_{s}^{t,x;\widehat{u}}, z_{s}^{t,x;\widehat{u}})_{s \in [t,T]}\) be the BSDE in (6) with \(\widehat{u} \in \mathcal{U}_{t,T}\). Let \(\widehat{y}_{s}^{\widehat{u}} := V(s,x_{s}^{t,x;\widehat{u}}) - y_{s}^{t,x; \widehat{u}}\) and \(\widehat{z}_{s}^{\widehat{u}} := \langle D V(s,x_{s}^{t,x; \widehat{u}}), \sigma (s,x_{s}^{t,x;\widehat{u}},\widehat{u}_{s}) \rangle + q(s,x_{s}^{t,x;\widehat{u}}) - z_{s}^{t,x;\widehat{u}}\). Note that \(\widehat{y}_{T}^{\widehat{u}} = 0\), \(\mathbb{P}\)-a.s. Then, we have
where \(A^{(1)}\) and \(A^{(2)}\) are bounded coefficients (independent of ŷ and ẑ) due to (H.1) and (H.2). Since (15) is a linear BSDE, in view of [13, Proposition 4.1.2], we have \(\widehat{y}_{s}^{\widehat{u}} = 0\) for \(s \in [t,T]\), \(\mathbb{P}\)-a.s. Hence, it holds that \(V(t,x_{t}^{t,x;\widehat{u}}) = V(t,x) = y_{t}^{t,x;\widehat{u}} = J(t,x; \widehat{u}) \), \(\mathbb{P}\)-a.s.
On the other hand, for any \(u \in \mathcal{U}_{t,T}\), by using the approach analogous to that above and (iii) of Lemma 1, we can show that \(\widehat{y}_{s}^{u} \leq 0\) for \(s \in [t,T]\), \(\mathbb{P}\)-a.s., which implies that \(V(t,x_{t}^{t,x;u}) = V(t,x) \leq y_{t}^{t,x;u} = J(t,x;u)\), \(\mathbb{P}\)-a.s. Note that the equality can be achieved when \(u = \widehat{u} \in \mathcal{U}_{t,T}\). This shows that for any \(u \in \mathcal{U}_{t,T}\) and \(x \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\), we have
where the last equality follows from the definition of the value function V in (8). This completes the proof of the theorem. □
Remark 5
In Sect. 3, we show the existence and uniqueness of the viscosity solution to the SHJB equation in (3). Furthermore, in the appendix, the existence and uniqueness of the weak solution to (3) is shown via the Sobolev-space technique.
2.3 General indefinite linear–quadratic problem with random coefficients
This subsection considers the general indefinite linear–quadratic (LQ) problem of (P) as an application of Theorem 2. For notational simplicity, we assume that \(r=1\), i.e., the one-dimensional Brownian motion.
The LQ problem in this subsection is referred to as (LQ-P) with
where A, F, C, E, Q, R are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted continuous stochastic processes with appropriate dimensions, which are uniformly bounded in \(\omega \in \Omega \) (they belong to \(\mathcal{L}_{\mathcal{F}}^{\infty }\)) and \(M \in L^{\infty }(\Omega ,\mathcal{F}_{T};\mathbb{S}^{n})\). We assume that Q, R, M are symmetric matrices, which need not be definite matrices.Footnote 5 When l in (16) is independent of y and z, (LQ-P) is reduced to the simplified LQ problem (with random coefficients) studied in [25, 26, 43–45] and the references therein.
From (4), the Hamiltonian can be written as (s argument is suppressed)
Assume that \(R_{s} + E_{s}^{\top }P E_{s}\) is (uniformly) positive-definite for almost all \(\omega \in \Omega \) and \(s \in [0,T]\). Then, we can easily see that H in (17) admits a unique minimizer, which can be written as follows:
By substituting (18) into (17), the SHJB in (3) is obtained by
where (s argument is suppressed)
In view of the verification theorem in Theorem 2, we need to seek for the solution of (19) to solve (LQ-P).
We conjecture that the general solutions for (19) are quadratic in x, i.e.,
where it is assumed that Λ, Λ̄ are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted symmetric \(n \times n\)-valued bounded stochastic processes with \(\Lambda _{T} = M\), i.e., \((\Lambda ,\bar{\Lambda }) \in \mathcal{L}_{\mathcal{F}}^{\infty }( \mathbb{S}^{n}) \times \mathcal{L}_{\mathcal{F}}^{2}(\mathbb{S}^{n})\). Under this assumption, V and q in (21) are smooth, i.e., \((V,q) \in \mathcal{L}^{\infty }_{\mathcal{F}}(C^{2}(\mathbb{R}^{n})) \times \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}^{n};\mathbb{R}^{1 \times r}))\), where \(D V(s,x) = \Lambda _{s} x\) and \(D q(s,x) = \bar{\Lambda }_{s} x\) are well defined. Then, by substituting (21) into (20), we can easily see that the SHJB equation in (19) admits a unique smooth solution if the following stochastic Riccati differential equation (SRDE) admits a unique solution:
Note that (22) is a symmetric \(n \times n\)-valued stochastic process. Here, the solution of the SRDE in (22) is defined by the adapted pair \((\Lambda ,\bar{\Lambda }) \in \mathcal{L}_{\mathcal{F}}^{\infty }( \mathbb{S}^{n}) \times \mathcal{L}_{\mathcal{F}}^{2}(\mathbb{S}^{n})\), which can be viewed as a matrix-valued BSDE with random coefficients.
By substituting (21) into (18), from Theorem 2, the optimal control for (LQ-P) can be obtained by
provided that \(R_{s} + E_{s}^{\top }\Lambda _{s} E_{s}\) is (uniformly) positive-definite for almost all \(\omega \in \Omega \) and \(s \in [0,T]\).Footnote 6
In summary, by applying the verification theorem in Theorem 2, we have the following result:
Proposition 2
Suppose that the pair \((\Lambda ,\bar{\Lambda }) \in \mathcal{L}_{\mathcal{F}}^{\infty }( \mathbb{S}^{n}) \times \mathcal{L}_{\mathcal{F}}^{2}(\mathbb{S}^{n})\) is the solution of the SRDE in (22) and that \(R_{s} + E_{s}^{\top }\Lambda _{s} E_{s}\) is (uniformly) positive-definite for almost all \(\omega \in \Omega \) and \(s \in [0,T]\). Then, for \(x \in L^{2}(\Omega ,\mathcal{F}_{t};\mathbb{R}^{n})\), \(V(t,x) = \frac{1}{2}\langle x, \Lambda _{t} x \rangle \) is the value function of (LQ-P) (equivalently, \(V(t,x) = \frac{1}{2}\langle x, \Lambda _{t} x \rangle \) is the optimal cost), and (23) is the corresponding optimal control.
Remark 6
The solvability of the SRDE in (22) is an open problem. When l does not depend on y and z, the solvability of the corresponding SRDEs has been discussed extensively in the literature; see [25, 26, 43–45] and the references therein. Moreover, we can consider the case of jump-diffusion models as in [63].
3 Viscosity solution of SHJB equation
This section introduces the notion of viscosity solutions for the SHJB equation in (3). Then, we show the existence of the viscosity solution for (3), i.e., the value function in (8) is the viscosity solution to (3). The uniqueness of the viscosity solution is also discussed under additional parameter assumptions.
3.1 Definition of viscosity solution
We note that the solution of (3) is the pair of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted random fields \((V,q)\). Due to the nonanticipativity of these two independent unknown components, it is inconvenient to define the notion of viscosity solutions for (3) by directly using the pair \((V,q)\). Instead, we introduce a class of random fields, by which the pair \((V,q)\) can be characterized.
Definition 1
The random field \(\phi :\Omega \times [0,T] \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) is said to be a class of \(\mathscr{S}^{2}_{\mathcal{F}}\), i.e., \(\phi \in \mathscr{S}^{2}_{\mathcal{F}}\), if \(\phi \in \mathcal{C}^{2}_{\mathcal{F}}(C(\mathbb{R}^{n})) \cap \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}^{n}))\) and there exists the pair  such that for any \(t \in [0,T]\) and \(x \in \mathbb{R}^{n}\), ϕ satisfies the following decomposition:
such that for any \(t \in [0,T]\) and \(x \in \mathbb{R}^{n}\), ϕ satisfies the following decomposition:

In Definition 1,  are two differential operators, which can be viewed as weak derivatives of ϕ with respect to time and sample variables. Similar notions of weak derivatives for Itô-type stochastic processes can be found in [64–66]. In fact, from the Doob–Meyer decomposition, the pair
are two differential operators, which can be viewed as weak derivatives of ϕ with respect to time and sample variables. Similar notions of weak derivatives for Itô-type stochastic processes can be found in [64–66]. In fact, from the Doob–Meyer decomposition, the pair  can be defined uniquely. Note that if ϕ is deterministic, then
can be defined uniquely. Note that if ϕ is deterministic, then  and
and  corresponds to the classical partial derivative of ϕ with respect to the time variable.
corresponds to the classical partial derivative of ϕ with respect to the time variable.  is also closely related to the Malliavin derivative if ϕ is smooth enough. We also mention that
is also closely related to the Malliavin derivative if ϕ is smooth enough. We also mention that  in Definition 1 is different from the notion of path derivatives for path-dependent stochastic processes in functional Itô-calculus.
in Definition 1 is different from the notion of path derivatives for path-dependent stochastic processes in functional Itô-calculus.
Suppose that the value function V satisfies Definition 1, i.e., \(V \in \mathscr{S}^{2}_{\mathcal{F}}\). Then, to solve the SHJB equation in (3), we have  . Hence, with Definition 1, it is easy to see that finding the pair \((V,q)\) for the solution of (3) is equivalent to finding V such that
. Hence, with Definition 1, it is easy to see that finding the pair \((V,q)\) for the solution of (3) is equivalent to finding V such that

In fact, the conversion from (3) to (24) via Definition 1 is a key step to define the notion of viscosity solutions.
Let \(B_{\delta }(x)\) be the Euclidean ball centered in \(x \in \mathbb{R}^{n}\) with radius \(\delta > 0\). For \(\delta > 0\), \(V \in \mathcal{C}_{\mathcal{F}}^{2}(C(\mathbb{R}^{n}))\), \(\kappa \in [0,T]\), \(\Omega _{\kappa } \in \mathcal{F}_{\kappa }\) with \(\mathbb{P}(\Omega _{\kappa }) > 0\), and \(\eta \in L^{2}(\Omega _{\kappa },\mathcal{F}_{\kappa };\mathbb{R}^{n})\), the semijets are defined as follows:

Then, the definition of viscosity solutions is given as follows. We modify the notion given in [11].
Definition 2
-
(i)
The random field \(V:\Omega \times [0,T] \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) with \(V \in \mathcal{C}^{2}(C(\mathbb{R}^{n}))\) is said to be a viscosity subsolution of the SHJB equation in (3), if \(W(T,x) \leq m(x)\) for \(x \in \mathbb{R}^{n}\), \(\mathbb{P}\)-a.s., and for \(\delta >0\), \(\kappa \in [0,T]\), \(\Omega _{\kappa } \in \mathcal{F}_{\kappa }\) with \(\mathbb{P}(\Omega _{\kappa }) > 0\), \(\eta \in L^{2}(\Omega _{\kappa },\mathcal{F}_{\kappa };\mathbb{R}^{n})\) and any \(\psi \in \mathcal{A}_{\delta }^{-}[V(\kappa ,\eta );\Omega _{\kappa }]\), it holds that (\(\mathbb{P}\)-a.s. in \(\Omega _{\kappa }\))
-
(ii)
The random field \(V:\Omega \times [0,T] \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) with \(V \in \mathcal{C}^{2}(C(\mathbb{R}^{n}))\) is said to be a viscosity supersolution of the SHJB equation in (3), if \(W(T,x) \geq m(x)\) for \(x \in \mathbb{R}^{n}\), \(\mathbb{P}\)-a.s., and for \(\delta >0\), \(\kappa \in [0,T]\), \(\Omega _{\kappa } \in \mathcal{F}_{\kappa }\) with \(\mathbb{P}(\Omega _{\kappa }) > 0\), \(\eta \in L^{2}(\Omega _{\kappa },\mathcal{F}_{\kappa };\mathbb{R}^{n})\) and any \(\psi \in \mathcal{A}_{\delta }^{+}[V(\kappa ,\eta );\Omega _{\kappa }]\), it holds that (\(\mathbb{P}\)-a.s. in \(\Omega _{\kappa }\))

-
(iii)
The random field \(V:\Omega \times [0,T] \times \mathbb{R}^{n} \rightarrow \mathbb{R}\) with \(V \in \mathcal{C}^{2}(C(\mathbb{R}^{n}))\) is said to be a viscosity solution of the SHJB equation in (3) if it is both a viscosity subsolution and a supersolution of (3).
Remark 7
-
(1)
If the coefficients in (3) are deterministic (they do not depend on \(\omega \in \Omega \)), then \(q = 0\) and (3) is reduced to the deterministic HJB equation given by
$$\begin{aligned} \textstyle\begin{cases} - \frac{\partial }{\partial s} V(s,x) = H(s,x,(V,D V,D^{2} V,0,0)(s,x)),\quad (s,x) \in [0,T) \times \mathbb{R}^{n}, \\ V(T,x) = m(x), \quad x \in \mathbb{R}^{n}. \end{cases}\displaystyle \end{aligned}$$In this case, Definition 2 becomes equivalent to the classical one in [46]. Various results on viscosity solutions for classical (deterministic) HJB equations can be found in [17, 18, 20] and the references therein.
-
(2)
When the coefficients are deterministic and dependent on the paths of x and B, (3) becomes the path-dependent HJB equation. This is a class of infinite-dimensional (deterministic) HJB equations. For path-dependent HJB equations, different notions of viscosity solutions were defined in [53–59]. Unlike the path-dependent case, in [53, 54, 56, 58], Definition 2 does not include the nonlinear expectation.
3.2 Existence and uniqueness of viscosity solution of (3)
We state the following existence result:
Theorem 3
Suppose that (H.1) and (H.2) hold. Then, the value function in (8) is a viscosity solution to the SHJB equation in (3).
Proof
We first prove that (8) is a viscosity supersolution.
In view of (H.1), (H.2) and Corollary 1, \(V \in \mathcal{C}^{2}(C(\mathbb{R}^{n}))\). Also, from (8), \(V(T,x) = m(x)\), \(\mathbb{P}\)-a.s. Then, from (ii) of Definition 2, for \(\delta >0\), \(\kappa \in [0,T]\), \(\Omega _{\kappa } \in \mathcal{F}_{\kappa }\) with \(\mathbb{P}(\Omega _{\kappa }) > 0\), \(\eta \in L^{2}(\Omega _{\kappa },\mathcal{F}_{\kappa };\mathbb{R}^{n})\) and any \(\psi \in \mathcal{A}_{\delta }^{+}[V(\kappa ,\eta );\Omega _{\kappa }]\), we need to show that (\(\mathbb{P}\)-a.s. in \(\Omega _{\kappa }\))

Suppose that V is not a viscosity supersolution, i.e., there exist \(\theta > 0\), \(\bar{\delta } > 0\) with \(\bar{\delta } \in (0,\delta )\), and \(\Omega ^{\prime }\in \mathcal{F}_{\kappa }\) with \(\Omega ^{\prime }\subset \Omega _{\kappa }\) and \(\mathbb{P}(\Omega ^{\prime }) > 0\) such that for \(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\), we have

Let

Note that

Then, for (25), in view of (H.1), (H.2) and the measurable selection theorem (see [11, Theorem A.1] and [60, 61]), there exists \(u_{t}^{\prime }\in U\) with \((u_{t}^{\prime })_{t \in [\kappa ,T]} \in \mathcal{U}_{\kappa ,T}\) such that (\(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\))

Let \(\hat{\kappa } := \inf \{s > \kappa : x_{s}^{\kappa ,\eta ;u^{\prime }} \notin B_{\bar{\delta }/2}(\eta ) \} \) and \(\tau \in (0,\bar{\delta }/4)\) with small τ. Then, we have \(\{\hat{\kappa } < \kappa + \tau \} \subseteq \{\max_{r \in [\kappa , \kappa +\tau ]} |x_{r}^{\kappa ,\eta ;u^{\prime }} - \eta | > \frac{\bar{\delta }}{2} \}\), which, together with Markov’s inequality and (i) of Lemma 1, implies (\(\mathbb{P}\)-a.s.)
On the other hand, from the DPP in Theorem 1, we have
where \(\bar{\kappa } := \kappa +\tau \wedge \hat{\kappa }\). Hence,
where, in view of the definition of Φ, Φ satisfies
Recall that

Then, by using the Itô–Kunita formula, we have (\(\mathbb{P}\)-a.s.)

Let
Hence, we have

where the second equality follows from (H.1) and (H.2). Note that \(F^{(1)}\) and \(F^{(2)}\) are bounded processes due to (H.1) and (H.2).
We can easily see that (29) is a linear BSDE, for which the explicit unique solution can be written as follows: [13, Proposition 4.1.2] (\(\mathbb{P}\)-a.s.)

where Z is the scalar-valued state transition process given by
From (ii) of Definition 2 and (28), we have (\(\mathbb{P}\)-a.s.)
which, together with (30), implies that

where

Since Z is a linear SDE, from (i) of Lemma 1, Lemma 2 and (27),
and due to (H.1), (H.2) and (i) of Lemma 1,
The estimates obtained above imply that

and for small τ (or as \(\tau \downarrow 0\)), with (26), we have (\(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\))

This leads to a contradiction; hence, V is a viscosity supersolution of (3).
For the proof of the viscosity-subsolution property, similar to the proof for the viscosity supersolution, if V is not a viscosity subsolution, then there exist \(\theta > 0\), \(\bar{\delta } > 0\) with \(\bar{\delta } \in (0,\delta )\), and \(\Omega ^{\prime }\in \mathcal{F}_{\kappa }\) with \(\Omega ^{\prime }\subset \Omega _{\kappa }\) and \(\mathbb{P}(\Omega ^{\prime }) > 0\) such that for \(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\), we have

As in (26), there exists \(u_{t}^{\prime }\in U\) with \((u_{t}^{\prime })_{t \in [\kappa ,T]} \in \mathcal{U}_{\kappa ,T}\) such that (\(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\))

Then, by using the Itô–Kunita formula and following the approach analogous to that for the viscosity-supersolution case, we can show that

and for small τ (or as \(\tau \downarrow 0\)), we have (\(\mathbb{P}\)-a.s. in \(\Omega ^{\prime }\))

which leads to a contradiction. This shows that V is a viscosity subsolution. This completes the proof of the theorem. □
We now discuss the uniqueness of the viscosity solution. It is assumed that
-
(H.3)
in (4), l does not depend on \(q+\langle p,\sigma \rangle \) (equivalently z in (6)). Moreover, for \(k > 2n + 2\) and any \(u \in \mathcal{U}_{0,T}\), we have \(f(\cdot ,\cdot ,u), \sigma (\cdot ,\cdot ,u) \in \mathcal{L}_{ \mathcal{F}}^{\infty }(W^{k,\infty }(\mathbb{R}^{n}))\), \(l(\cdot ,\cdot ,u,y) \in \mathcal{L}_{\mathcal{F}}^{2}(H^{k}( \mathbb{R}^{n}))\), and \(m \in L^{2}(\Omega ,\mathcal{F}_{T};H^{k}(\mathbb{R}^{n}))\).
The first uniqueness result states that the value function is the maximal-viscosity solution [11, Theorem 5.2].
Theorem 4
Suppose that (H.1)–(H.3) hold. Assume that v is the viscosity solution of (3) with \(v^{+} \in \mathcal{C}^{2}(C(\mathbb{R}^{n}))\), where \(v^{+}\) denotes the nonnegative part of v. Then, for \(s \in [0,T]\) and \(x \in \mathbb{R}^{n}\), we have \(v(s,x) \leq V(s,x)\), \(\mathbb{P}\)-a.s., where V is the value function of (P) defined in (8).
Remark 8
In [11, Theorem 5.2], although the running cost l (f in [11]) does not depend on both y and \(q+\langle p,\sigma \rangle \), we can easily extend the proof of [11, Theorem 5.2] to the case when it depends on y. In fact, in the proof of [11, Theorem 5.2], the modified Feynman–Kac formula for SPDEs (see [6, Theorem 4.3]), together with the optimal stopping theory, is applied to construct an appropriate test function ψ, where the regularity with respect to y is not required. However, when the running cost depends on \(q+\langle p,\sigma \rangle \) as in (4), the Feynman–Kac formula needs a high regularity with respect to this term, which has not been solved in the literature. We will address the general uniqueness problem in the near future.
We introduce the superparabolicity assumption:
-
(H.4)
Assume that \(B = [ B^{(1)}\ B^{(2)} ] \), where \(B^{(1)}\) and \(B^{(1)}\) are mutually independent \(r_{1}\)- and \(r_{2}\)-dimensional Brownian motions (\(r = r_{1} + r_{2}\)), respectively, where \(\{\mathcal{F}_{s}^{(1)}\}_{s \geq 0}\) is the filtration generated by \(B^{(1)}\). Let \(\sigma = [ \sigma ^{(1)} \ \sigma ^{(2)} ] \) be the corresponding diffusion part (note that \(\sigma ^{(1)}\) is \(n \times r_{1}\)). m is \(\mathcal{F}_{T}^{(1)}\)-measurable, and l, f are \(\mathcal{F}_{s}^{(1)}\)-measurable. \(l,m \geq 0\) for all \((\omega ,s,x,u,y) \in \Omega \times [0,T] \times \mathbb{R}^{n} \times U \times \mathbb{R}\), \(\mathbb{P}\)-a.s. σ is not random, i.e., it does not depend explicitly on \(\omega \in \Omega \). For \((s,x,u,w) \in [0,T] \times \mathbb{R}^{n} \times U \times \mathbb{R}^{n}\), there exists \(C > 0\) such that \(\sum_{i,j=1}^{n} \sum_{k=1}^{r_{2}} (\sigma ^{(2)})^{ik} (\sigma ^{(2)})^{jk} w^{i} w^{j} \geq C |w|^{2}\), where the superscript i indicates the ith component of the vector.
Based on [11, Theorem 5.6], we have the second uniqueness result:
Theorem 5
Assume that (H.1)–(H.4) hold. Then, the value function in (8) is the unique viscosity solution of the SHJB equation in (3), which is \(\mathcal{F}^{(1)}_{t}\)-measurable for \(t \in [0,T]\) and \(x \in \mathbb{R}^{n}\).
Remark 9
The proof in [11, Theorem 5.6] relies on approximating the coefficients in (3) via the density argument and the existence and uniqueness of the viscosity solution for parabolic PDEs with the approximated coefficients for a small time interval. As noted in Remark 8, the proof of [11, Theorem 5.6] can easily be extended to the case when l depends on y. See also [11, Remark 5.2] for the discussion on (H.4).
Remark 10
By Theorem 5, the value function in (8) can be characterized using the (viscosity) solution of the SHJB equation in (3).
4 Applications
In this section, we consider two different applications of (P) in Sect. 2; the utility-maximization problem and the European option-pricing problem.
4.1 Utility maximization with random coefficients
The first application is the utility-maximization problem with random coefficients for the investor, which can be viewed as an extension of the case with deterministic coefficients studied in the literature (e.g., [20, 47, 48]).
We consider the financial market, where the nonrisky (risk-free) asset is with the unit price, i.e., \(x_{t}^{(0)}= 1\) for \(t \in [0,T]\). The dynamics of the (\(\mathbb{R}\)-valued) risky asset (stock) satisfies the SDE given by
where r is the stock appreciation rate and σ is the volatility, which are continuous, bounded and \(\{\mathcal{F}_{s}\}_{s \geq 0 }\)-adapted stochastic processes. Let μ be the interest rate of borrowing and/or lending money, which is a continuous, bounded and \(\{\mathcal{F}_{s}\}_{s \geq 0 }\)-adapted stochastic process.
According to [20, 48] (see [20, Chap. 2.4]), under the assumption that (i) the stock processes are continuously traded over \([0,T]\), (ii) there are no other expenses such as taxes and transaction costs, and (iii) the market satisfies the self-financing condition, based on \(x_{t}^{(0)}\) and (31), and by introducing the portfolio strategy u, the (\(\mathbb{R}\)-valued) wealth process of the investor can be described by the following SDE:
We introduce the following recursive-type BSDE objective functional capturing the utility of the agent:
Then, our problem corresponds to the maximization of the utility over the admissible portfolio strategy \(u \in \mathcal{U}_{t,T}\) subject to the wealth process in (32), i.e.,
where
Note that this is a special case of (P) in Sect. 2 and is an extension of the utility-maximization problem with deterministic coefficients studied in [20, 47, 48]. We can easily check that (32) and (33) hold (H.1)–(H.3) and have unique solutions from Lemma 1.
The corresponding SHJB equation can be obtained by
where
Note that (36) attains the maximum, provided that \(P < 0\),
By substituting (37) into (36), the SHJB equation in (35) becomes
where
In summary, from the verification theorem in Theorem 2, we state the following result.
Proposition 3
Suppose that the pair \((V,q) \in \mathcal{L}^{\infty }_{\mathcal{F}}(C^{2}(\mathbb{R})) \times \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}))\) is the solution to the SHJB equation in (38), where \(D V(s,X) < 0\) for all \((s,X) \in [0,T] \times \mathbb{R}\). Then, the corresponding optimal investment strategy of the utility-maximum problem in (34) can be written as
Moreover, the optimal utility of the agent is given by
Remark 11
In view of Proposition 3, (39) is the optimal investment strategy for the utility-maximization problem, which can be obtained using the solution of the SHJB equation in (38). Note that the SHJB equation in (38) admits a unique viscosity solution from Theorems 3–5 (or the weak solution from Theorem 6.1). Then, we may apply numerical techniques of SPDEs (see [37, 38, 67] and the references therein) to characterize the solution of (38).
4.2 European option pricing with random coefficients
The second example we consider is the (recursive-type) European option-pricing problem with random coefficients, which can be viewed as an extension of the case with deterministic coefficients studied in the literature (e.g., [12, 13, 20]).
Recall the risky asset (stock) process \((x_{s}^{(1)})_{s \in [t,T]}\) in (31). For the European option-pricing problem, the wealth process in (32) becomes the BSDE given by
where \(x_{T}^{(1)}\) is the terminal value of the risky asset (stock) process in (31) and \(m(x_{T}^{(1)})\) captures an \(\mathcal{F}_{T}\)-measurable contingent claim determined by the stock process. Assume that there exists π such that \(r_{s} - \mu _{s} = \sigma _{s} \pi _{s}\). This is called the risk-premium process. Then, (40) can be rewritten as the BSDE form as follows:
In other words, in (41), a European contingent claim \(m(x_{T}^{(1)})\) settled at time T is \(\mathcal{F}_{T}\)-measurable. It can be thought of as a contract that pays \(m(x_{T}^{(1)})\) at maturity T. Then, the European option-pricing problem is to find \(u^{*} \in \mathcal{U}_{t,T}\) such that the initial wealth \(J_{\mathtt{E}}(t,a;u^{*}) = y_{t}^{t,a;u^{*}}\) achieves the contingent claim \(m(x_{T}^{(1)})\) subject to (31) and (41). Note that unlike the utility-maximization problem in (34), the wealth process in (41) is the BSDE with random coefficients, which is the recursive-type objective functional. We can easily see that the European option-pricing problem in (31) and (41) is a special case of (P), which holds (H.1) and (H.2).
Note that in view of (ii) of Lemma 1, the wealth process in (41) admits a unique solution of \((y_{s}^{t,a;u},z_{s}^{t,a;u})_{s \in [t,T]} \in \mathcal{C}_{ \mathcal{F}}^{2}(\mathbb{R}) \times \mathcal{L}_{\mathcal{F}}^{2}( \mathbb{R})\), and by Theorem 2, its solution can be obtained by solving the following SHJB equation:
where
Based on the analysis given above, the proof of Theorem 2, and [6, Theorem 4.3], we state the following result.
Proposition 4
Suppose that the pair \((V,q) \in \mathcal{L}^{\infty }_{\mathcal{F}}(C^{2}(\mathbb{R})) \times \mathcal{L}^{2}_{\mathcal{F}}(C^{2}(\mathbb{R}))\) is the solution to the SHJB equation in (42). Then, the optimal portfolio strategy of the European option-pricing problem can be written as
The solution of (41) is given by
and the optimal initial wealth of the European option-pricing problem is
Remark 12
A similar argument to Remark 11 can be applied to Proposition 4. In particular, from Proposition 4, (43) is the optimal portfolio strategy for the European option-pricing problem, which achieves the corresponding contingent claim for the investor. Note that (43) is obtained using the solution of the SHJB equation in (42), which can be characterized by applying numerical techniques of SPDEs (see [37, 38, 67] and the references therein).
5 Conclusions
We have considered the stochastic optimal control problem with random coefficients under the recursive-type objective functional captured by the BSDE. Due to the recursive-type BSDE objective functional with random coefficients, the problem in this paper introduces several technical intricacies, which do not appear in the existing literature. Using the backward semigroup associated with the recursive-type objective functional and the estimates of BSDEs, we have shown the DPP for the value function as well as its continuity. Then, by using the Itô–Kunita formula and the estimates of BSDEs, we have obtained the verification theorem, which constitutes the sufficient condition for optimality and characterizes the value function, provided that the solution of the SHJB equation exists. Furthermore, we have studied the existence and uniqueness of the solution to the SHJB equation under two different weak-solution concepts. First, under appropriate assumptions, we have shown the existence and uniqueness of the weak solution via the Sobolev-space technique, which requires converting the SHJB equation to a class of backward stochastic evolution equations. Secondly, we have proven that the value function is the viscosity solution to the SHJB equation by constructing the auxiliary BSDE in terms of the value function, and using the DPP and the precise estimates of BSDEs (including the linear BSDE theory and the continuity of the value function). For applications, we have considered the linear–quadratic problem, the utility-maximization problem, and the European option-pricing problem. In contrast to the existing literature, each problem is formulated by the generalized recursive-type objective functional and is subject to random coefficients. By applying the theoretical results of this paper, we have obtained the explicit optimal solution for each problem in terms of the solution of the corresponding SHJB equation.
There are several interesting future research problems:
-
(1)
One important problem is the uniqueness of the viscosity solution for the SHJB equation in (3) without additional parameter assumptions. This requires us to obtain the generalized Feynman–Kac formula between BSDEs and SPDEs;
-
(2)
We can also consider the case of fully coupled forward–backward SDEs, where f and σ in (5) are also dependent on the BSDE. This will induce a more complicated SHJB equation with an additional algebraic equation; see [68, 69] for the deterministic coefficients case;
-
(3)
The (existence and uniqueness) solvability of the SRDE in (22) needs to be studied, which requires the extension of techniques in [25, 43–45];
-
(4)
Applications to various mathematical finance problems are also an interesting avenue to pursue.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
Specifically, given a family of \(\mathbb{R}\)-valued random variables \(\nu _{l}\) with \(l \in H\), a random variable ν is said to be \(\operatorname*{ess\,inf}_{l \in H} \nu _{l}\) if (i) \(\nu \leq \nu _{l}\), \(\mathbb{P}\)-a.s., for any \(l \in H\) and (ii) if there is another random variable \(\nu ^{\prime }\) such that \(\nu ^{\prime }\leq \nu _{l}\), \(\mathbb{P}\)-a.s., for any \(l \in H\), then \(\nu ^{\prime }\leq \nu \), \(\mathbb{P}\)-a.s. Note that \(\operatorname*{ess\,sup}_{l \in H} \nu _{l} = - \operatorname*{ess\,inf}_{l \in H} (-\nu _{l})\).
In order to apply the verification theorem in Theorem 2 to (LQ-P), we take \(x \in X\) and \(u \in U\) in (16) (particularly for l and m in (16)), where U and X need to be restricted to appropriate sufficiently large compact subsets of \(\mathbb{R}^{m}\) and \(\mathbb{R}^{n}\), respectively; see [19, Chap. 6] for a related discussion. Then clearly, (16) satisfies (H.1) and (H.2).
This holds when \(R_{s}\) and \(\Lambda _{s}\) are (uniformly) positive-definite for almost all \(\omega \in \Omega \) and \(s \in [0,T]\).
Note that \((W^{k,q}(\mathbb{R}^{n}),\|\cdot \|_{k,q})\) is a Banach space and \((H^{k},\|\cdot \|_{k})\) is a Hilbert space [51].
For \(f \in \mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))\), the weak derivatives of f up to kth-order are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted stochastic processes, which belong to \(\mathcal{L}_{\mathcal{F}}^{2}\).
References
Peng, S.: Stochastic Hamilton–Jacobi–Bellman equations. SIAM J. Control Optim. 30(2), 284–304 (1992)
Ma, J., Yong, J.: On linear, degenerate backward stochastic partial differential equations. Probab. Theory Relat. Fields 113, 135–170 (1999)
Hu, Y., Ma, J., Yong, J.: On semi-linear degenerate backward stochastic partial differential equations. Probab. Theory Relat. Fields 123, 381–411 (2002)
Tang, S.: Semi-linear systems of backward stochastic partial differential equations in \(\mathbb{R}^{n}\). Chin. Ann. Math. 26(3), 437–456 (2012)
Du, K., Qui, J., Tang, S.: \(L^{p}\) theory for super-parabolic backward stochastic partial differential equations in the whole space. Appl. Math. Optim. 65, 175–219 (2012)
Du, K., Zhang, Q.: Semi-linear degenerate backward stochastic partial differential equations and associated forward–backward stochastic differential equations. Stoch. Process. Appl. 123, 1616–1637 (2013)
Chen, S., Tang, S.: Semi-linear backward stochastic integral partial differential equations driven by a Brownian motion and a Poisson point process. Math. Control Relat. Fields 5(3), 401–434 (2015)
Qiu, J.: Weak solution for a class of fully nonlinear stochastic Hamilton–Jacobi–Bellman equations. Stoch. Process. Appl. 127, 1926–1959 (2017)
Tang, S., Wei, W.: On the Cauchy problem for backward stochastic partial differential equations in Hölder spaces. Ann. Probab. 44(1), 360–398 (2016)
Peng, S.: Open problems on backward stochastic differential equations. In: Chen, S., Li, X., Yong, J., Zhou, X.Y. (eds.) Control of Distributed Parameter and Stochastic Systems. IFIP Advances in Information and Communication Technology, pp. 265–273. Springer, Berlin (1999)
Qiu, J.: Viscosity solutions of stochastic Hamilton–Jacobi–Bellman equations. SIAM J. Control Optim. 56(5), 3708–3730 (2018)
El-Karoui, N., Peng, S., Quenez, M.C.: Backward stochastic differential equations in finance. Math. Finance 7(1), 1–71 (1997)
Zhang, J.: Backward Stochastic Differential Equations: From Linear to Fully Nonlinear Theory. Springer, Berlin (2017)
Moon, J.: Generalized risk-sensitive optimal control and Hamilton–Jacobi–Bellman equation. IEEE Trans. Autom. Control 66(5), 2319–2325 (2021)
Wang, G., Wu, Z.: The maximum principles for stochastic recursive optimal control problems under partial information. IEEE Trans. Autom. Control 54(6), 1230–1242 (2009)
Peng, S.: A generalized dynamic programming principle and Hamilton–Jacobi–Bellman equation. Stoch. Stoch. Rep. 38, 119–134 (1992)
Fleming, W., Soner, H.M.: Controlled Markov Processes and Viscosity Solutions, 2nd edn. Springer, Berlin (2006)
Yong, J., Zhou, X.Y.: Stochastic Controls: Hamiltonian Systems and HJB Equations. Springer, Berlin (1999)
Başar, T., Olsder, G.J.: Dynamic Noncooperative Game Theory, 2nd edn. SIAM, Philadelphia (1999)
Touzi, N.: Optimal Stochastic Control, Stochastic Target Problems, and Backward SDE. Springer, Berlin (2013)
Buckdahn, R., Li, J.: Stochastic differential games and viscosity solutions of Hamilton–Jacobi–Bellman–Isaacs equations. SIAM J. Control Optim. 47(4), 444–475 (2008)
Wu, Z., Yu, Z.: Dynamic programming principle for one kind of stochastic recursive optimal control problem and Hamilton–Jacobi–Bellman equation. SIAM J. Control Optim. 47(5), 2616–2641 (2008)
Chen, L., Wu, Z.: Dynamic programming principle for stochastic recursive optimal control problem with delayed systems. ESAIM Control Optim. Calc. Var. 18, 1005–1026 (2012)
Hu, M.: Stochastic global maximum principle for optimization with recursive utilities. Probab. Uncertain. Quant. Risk 2(1), 1–20 (2017)
Hu, Y., Zhou, X.Y.: Indefinite stochastic Riccati equations. SIAM J. Control Optim. 42(1), 123–137 (2003)
Moon, J., Duncan, T.E.: A simple proof of indefinite linear–quadratic stochastic optimal control with random coefficients. IEEE Trans. Autom. Control 65(12), 5422–5428 (2020)
Bismut, J.M.: Linear–quadratic optimal stochastic control with random coefficients. SIAM J. Control Optim. 14(3), 419–444 (1976)
Sun, J., Xiong, J., Yong, J.: Indefinite stochastic linear–quadratic optimal control problems with random coefficients: closed-loop representation of open-loop optimal controls. Ann. Appl. Probab. 31(1), 460–499 (2021)
Wang, H., Wu, Z.: Time-inconsistent optimal control problem with random coefficients and stochastic equilibrium HJB equation. Math. Control Relat. Fields 5(3), 651–678 (2015)
Mitsui, K., Tabata, Y.: A stochastic linear–quadratic problem with Lévy processes and its application to finance. Stoch. Process. Appl. 118, 120–152 (2008)
Cordon, F., Di Persio, L.: Optimal control for the stochastic FitzHugh–Nagumo model with recovery variable. Evol. Equ. Control Theory 7(4), 571–585 (2018)
Hocquet, A., Vogler, A.: Optimal control of mean field equations with monotone coefficients and applications in neuroscience. Appl. Math. Optim. 84, 1925–1968 (2021). https://doi.org/10.1007/s00245-021-09816-1
Imkeller, P., Reveillac, A.: Solvability and numerical simulation of BSDEs related to BSPDEs with applications to utility maximization. Int. J. Theor. Appl. Finance 14(5), 635–667 (2011)
Sen, N., Caines, P.: Mean field games with partial observations. SIAM J. Control Optim. 57(3), 2064–2091 (2019)
Haussmann, U.G.: The maximum principle for optimal control of diffusions with partial information. SIAM J. Control Optim. 25(2), 341–361 (1987)
Handel, R.: Stochastic Calculus, Filtering, and Stochastic Control (2007) https://web.math.princeton.edu/ rvan/acm217/ACM217.pdf
Zhang, Z., Em Karniadakis, G.: Numerical Methods for Stochastic Partial Differential Equations with White Noise. Springer, Berlin (2017)
Zhang, D., Gun, L., Em Karniadakis, G.: Learning in modal space: solving time-dependent stochastic PDEs using physics-informed neural networks (2019) https://arxiv.org/abs/1905.01205
Pham, H.: Linear quadratic optimal control of conditional McKean–Vlasov equation with random coefficients and applications. Probab. Uncertain. Quant. Risk 1(7), 1–26 (2016)
Nourian, M., Caines, P.E.: ϵ-Nash mean field game theory for nonlinear stochastic dynamical systems with major and minor agents. SIAM J. Control Optim. 51(4), 3302–3331 (2013)
Ren, M., Zhang, J., Wang, H.: Minimized tracking error randomness control for nonlinear multivariate and non-Gaussian systems using the generalized density evolution equation. IEEE Trans. Autom. Control 59(9), 2486–2490 (2014)
Boutselis, G.I., Pereira, M., Theodorou, E.A.: Variational inference for stochastic control of infinite dimensional systems (2018) https://arxiv.org/abs/1809.03035
Kohlmann, M., Tang, S.: Multidimensional backward stochastic Riccati equations and applications. SIAM J. Control Optim. 41(6), 1696–1721 (2003)
Tang, S.: Dynamic programming for general linear quadratic optimal stochastic control with random coefficients. SIAM J. Control Optim. 53(2), 1082–1106 (2015)
Du, K.: Solvability conditions for indefinite linear quadratic optimal stochastic control problems and associated stochastic Riccati equations. SIAM J. Control Optim. 53(6), 3673–3689 (2015)
Crandall, M.G., Ishii, H., Lions, P.-L.: User’s guide to viscosity solutions of second order partial differential equations. Bull. Am. Math. Soc. 27, 1–67 (1992)
Junghenn, H.D.: Option Valuation. CRC Press, Boca Raton (2011)
Shreve, S.E.: Stochastic Calculus for Finance II. Springer, Berlin (2000)
Huang, M., Caines, P.E., Malhame, R.P.: Uplink power adjustment in wireless communication systems: a stochastic control analysis. IEEE Trans. Autom. Control 49(10), 1693–1708 (2004)
Huang, M., Malhame, R., Caines, P.E.: Computationally tractable stochastic power control laws in wireless communications. IEEE Trans. Autom. Control 50(2), 263–268 (2005)
Evans, L.C.: Partial Differential Equations, 2nd edn. Am. Math. Soc., Providence (2010)
Karatzas, I., Shreve, S.E.: Methods of Mathematical Finance. Springer, Berlin (1998)
Ekren, I., Keller, C., Touzi, N., Zhang, J.: On viscosity solutions of path dependent PDEs. Ann. Probab. 42(1), 204–236 (2014)
Pham, T., Zhang, J.: Two-person zero-sum game in weak formulation and path dependent Bellman–Isaacs equation. SIAM J. Control Optim. 52(4), 2090–2121 (2014)
Tang, S., Zhang, F.: Path-dependent optimal stochastic control and viscosity solution of associated Bellman equations. Discrete Contin. Dyn. Syst. 35(11), 5521–5553 (2015)
Ekren, I., Touzi, N., Zhang, J.: Viscosity solutions of fully nonlinear parabolic path dependent PDEs: part I. Ann. Probab. 44(2), 1212–1253 (2016)
Zhang, F.: The existence of game value for path-dependent stochastic differential game. SIAM J. Control Optim. 55(4), 2519–2542 (2017)
Possamai, D., Touzi, N., Zhang, J.: Zero-sum path-dependent stochastic differential games in weak formulation. Ann. Appl. Probab. 30(3), 1415–1457 (2020)
Moon, J.: State and control paths-dependent stochastic zero-sum differential games: dynamic programming principle and viscosity solution of paths-dependent Hamilton–Jacobi–Isaacs Equation (2019) https://arxiv.org/abs/1911.00315
Wagner, D.H.: Survery on measurable selection theorems. SIAM J. Control Optim. 15(5), 859–903 (1977)
Rieder, U.: Measurable selection theorems for optimization problems. Manuscr. Math. 24, 115–131 (1978)
Kunita, H.: École d’Été de Probabilités de Saint-Flour XII – 1982. Springer, Berlin (1984)
Li, N., Yu, Z.: Recursive stochastic linear quadratic optimal control and nonzero-sum differential game problem with random jumps. Adv. Differ. Equ. 2015, 144 (2015)
Cont, R., Fournié, D.: Change of variable formulas for non-anticipative functionals on path space. J. Funct. Anal. 259, 1043–1072 (2010)
Cont, R., Fournié, D.: Functional Itô calculus and stochastic integral representation of martingales. Ann. Probab. 41(1), 109–133 (2013)
Leao, D., Ohashi, A., Simas, A.B.: A weak version of path-dependent functional Itô calculus. Ann. Probab. 46(6), 3399–3441 (2018)
Ma, X., Zabaras, N.: An adaptive high-dimensional stochastic model representation technique for the solution of stochastic partial differential equations. J. Comput. Phys. 229, 3884–3915 (2010)
Li, J., Wei, Q.: Optimal control problems of fully coupled FBSDEs and viscosity solutions of Hamilton–Jacobi–Bellman equations. SIAM J. Control Optim. 52(3), 1622–1662 (2014)
Hu, M., Ji, S., Xue, X.: The existence and uniqueness of viscosity solution to a kind of Hamilton–Jacobi–Bellman equations. SIAM J. Control Optim. 57(6), 3911–3938 (2019)
Attouch, H., Buttazzo, G., Michaille, G.: Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization, 2nd edn. SIAM, Philadelphia (2014)
Hu, Y., Peng, S.: Adapted solution of a backward semilinear stochastic evolution equation. Stoch. Anal. Appl. 9(4), 445–459 (1991)
Acknowledgements
The author thanks Prof. Wonhee Kim for his comments on the earlier version of this paper.
Funding
This research was supported in part by the National Research Foundation of Korea (NRF) Grant funded by the Ministry of Science and ICT, South Korea (NRF-2017R1A5A1015311, NRF-2021R1A2C2094350) and in part by the Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2020-0-01373, Artificial Intelligence Graduate School Program (Hanyang University)).
Author information
Authors and Affiliations
Contributions
JM: problem formulation, analysis, writing, revising, and editing. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that they have no competing interests.
Appendix: Existence and uniqueness of the weak solution to the SHJB equation
Appendix: Existence and uniqueness of the weak solution to the SHJB equation
In this appendix, we show the existence and uniqueness of the (weak) solution to the SHJB equation in (3) using the Sobolev-space approach. For simplicity, we consider the one-dimensional Brownian motion case (\(r=1\)).
Recall that \((W^{k,q}(\mathbb{R}^{n}),\|\cdot \|_{k,q})\) is the Sobolev space for real-valued functions on \(\mathbb{R}^{n}\) (in the sense of weak derivatives in \(\mathbb{R}^{n}\)) and \(H^{k} := W^{k,2}\) with \(\|\cdot \|_{k} := \|\cdot \|_{k,2}\).Footnote 7 Also, \(L^{2}(\mathbb{R}^{n})\) is the (Hilbert) space of square-integrable real-valued functions on \(\mathbb{R}^{n}\) and \(\mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))\) is the set of \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted \(H^{k}(\mathbb{R}^{n})\)-valued random processes with norm \(\|\cdot \|_{\mathcal{L}_{\mathcal{F}}^{2}(H^{k}(\mathbb{R}^{n}))} = \mathbb{E}[\int _{0}^{T} \|\cdot \|_{k}^{2} \,\mathrm{d}s]\).Footnote 8 We identify \(L^{2}(\mathbb{R}^{n})\) with its dual space. Then, we have
where \(H^{-1}(\mathbb{R}^{n})\) is the dual space of \(H^{1}(\mathbb{R}^{n})\). Define \((H^{1}(\mathbb{R}^{n}), L^{2}(\mathbb{R}^{n}),H^{-1}(\mathbb{R}^{n})) =: (\mathbb{V},\mathbb{H},\mathbb{V}^{\prime })\) [51, 70]. Let \(\mathscr{L}^{2}(\mathbb{V};\mathbb{V}^{\prime })\) be the space of bounded operators from \(\mathbb{V}\) to \(\mathbb{V}^{\prime }\). Note that \(\|\cdot \|_{\mathbb{V}} = \|\cdot \|_{1}\). Let \(\langle \cdot ,\cdot \rangle _{\mathbb{V},\mathbb{V}^{\prime }}\) be the duality pairing between \(\mathbb{V}\) and \(\mathbb{V}^{\prime }\). Let \(\langle \cdot ,\cdot \rangle _{\mathbb{H}}\) be the inner product on \(\mathbb{H}\), and \(\|\cdot \|_{\mathbb{H}} := \langle \cdot ,\cdot \rangle _{\mathbb{H}}^{1/2} \) the norm defined on \(\mathbb{H}\).
We consider the following BSDE:
where the coefficients are defined by
The BSDE in (A.1) can be viewed as a class of backward stochastic evolution equations [6, 71]. It is assumed that
-
(A)
\(\mathcal{A}\), ψ and ψ̂ are \(\{\mathcal{F}_{s}\}_{s \geq 0}\)-adapted stochastic processes in \(\mathcal{L}^{2}_{\mathcal{F}}\). \(\mathcal{A}\) is bounded for \((s,\omega ) \in [0,T] \times \Omega \) and for any \(v \in \mathbb{V}\), \(\langle \mathcal{A}_{s} v,v\rangle _{\mathbb{V},\mathbb{V}^{\prime }} \geq 0\). For \(z_{1},z_{2} \in \mathbb{H}\) and \(y \in \mathbb{V}\), there exists a constant \(K>0\) such that
$$\begin{aligned} \bigl\langle \psi (s,z_{1}) - \psi (s,z_{2}), y \bigr\rangle _{\mathbb{V}, \mathbb{V}^{\prime }} \leq K \Vert z_{1} - z_{2} \Vert _{\mathbb{H}} \langle 2 \mathcal{A}_{s} y, y \rangle _{\mathbb{V},\mathbb{V}^{\prime }}^{1/2}. \end{aligned}$$ψ̂ is Lipschitz continuous in \((y,z) \in \mathbb{V} \times \mathbb{H}\). η is \(\mathcal{F}_{T}\)-measurable.
Then, in view of [71, Theorem 4.1] (see also [1, Lemma 4.2]), we have the following result:
Lemma 6.1
Suppose that (A) holds. Then, (A.1) admits a unique solution of \((\mathcal{Y}_{s},\mathcal{Z}_{s})_{s \in [0,T]} \in \mathcal{L}^{2}_{ \mathcal{F}}(\mathbb{V}) \times \mathcal{L}^{2}_{\mathcal{F}}( \mathbb{H})\).
Below, the existence and uniqueness of the weak solution to the SHJB equation in (3) is shown. We assume that
-
(B)
σ is independent of u, and \(l(s,x,u,y,z) = l(s,x,u,y) + z\). For almost all \(\omega \in \Omega \), f, l, m and σ are continuous in \((x,u) \in \mathbb{R}^{n} \times U\) and bounded on \(\mathbb{R}^{n}\). For almost all \(\omega \in \Omega \) and \((s,u) \in [0,T] \times U\), f, l, m and σ are continuously differentiable in x, which are bounded on \(\mathbb{R}^{n} \) and continuous in \(s \in [0,T]\).
We define
and for \(\gamma \in \mathbb{H}\) and \(\zeta \in \mathbb{V}\),
where \(\partial _{x_{i}}\) is the partial derivative with respect to \(x_{i}\) with \(x= [ x_{1}\ \cdots \ x_{n} ] ^{\top }\in \mathbb{R}^{n}\) and \((\sigma \sigma ^{\top }(s,x))_{ij}\) denotes the ith-row and jth-column elements of \(\sigma \sigma ^{\top }\).
Clearly, under (B), it can be easily verified that \(\mathcal{A}\), ψ and ψ̂ satisfy the conditions for the coefficients of the BSDE in (A.1) and (A). Also, by using the integration by parts formula, for any \(\zeta , \beta \in \mathbb{V}\) and \(\gamma \in \mathbb{H}\), we can show that
Now, the weak solution of the SHJB equation is defined as follows [1–3, 5, 6]:
Definition 6.1
The pair \((V, q) \in \mathcal{L}^{2}_{\mathcal{F}}(\mathbb{V}) \times \mathcal{L}^{2}_{\mathcal{F}}(\mathbb{H})\) is said to be a weak solution to the SHJB equation in (3) if for each \(\beta \in \mathbb{V}\), the pair \((V, q)\) satisfies
Note that if there is a smooth (classical) solution of the SHJB equation in (3), it is also a weak solution in the sense of Definition 6.1. Based on Lemma 6.1 and the analysis given above (particularly (A.2)), the existence and uniqueness of the weak solution to (3) in the sense of Definition 1 can be stated as follows:
Theorem 6.1
Assume that (B) holds. Then, the pair \((V, q) \in \mathcal{L}^{2}_{\mathcal{F}}(\mathbb{V}) \times \mathcal{L}^{2}_{\mathcal{F}}(\mathbb{H})\) is a unique weak solution of the SHJB equation in (3).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moon, J. Stochastic optimal control with random coefficients and associated stochastic Hamilton–Jacobi–Bellman equations. Adv Cont Discr Mod 2022, 3 (2022). https://doi.org/10.1186/s13662-021-03674-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03674-5