- Research Article
- Open access
- Published:
Positive Solutions for Multiparameter Semipositone Discrete Boundary Value Problems via Variational Method
Advances in Difference Equations volume 2008, Article number: 840458 (2008)
Abstract
We study the existence, multiplicity, and nonexistence of positive solutions for multiparameter semipositone discrete boundary value problems by using nonsmooth critical point theory and subsuper solutions method.
1. Introduction
Let  and
and  be the set of all integers and real numbers, respectively. For
be the set of all integers and real numbers, respectively. For  , define
, define  ,
,  , when
, when  .
.
In this paper, we consider the multiparameter semipositone discrete boundary value problem

where  are parameters,
are parameters,  is a positive integer,
is a positive integer,  is the forward difference operator,
is the forward difference operator,  ,
,  is a continuous positive function satisfying
is a continuous positive function satisfying  , and
, and  is continuous and eventually strictly positive with
is continuous and eventually strictly positive with  .
.
We notice that for fixed  ,
,  whenever
whenever  is sufficiently small. We call (1.1) a semipositone problem. Semipositone problems are derived from [1], where Castro and Shivaji initially called them nonpositone problems, in contrast with the terminology positone problems, put forward by Keller and Cohen in [2], where the nonlinearity was positive and monotone. Semipositone problems arise in bulking of mechanical systems, design of suspension bridges, chemical reactions, astrophysics, combustion, and management of natural resources; for example, see [3–6].
is sufficiently small. We call (1.1) a semipositone problem. Semipositone problems are derived from [1], where Castro and Shivaji initially called them nonpositone problems, in contrast with the terminology positone problems, put forward by Keller and Cohen in [2], where the nonlinearity was positive and monotone. Semipositone problems arise in bulking of mechanical systems, design of suspension bridges, chemical reactions, astrophysics, combustion, and management of natural resources; for example, see [3–6].
In general, studying positive solutions for semipositone problems is more difficult than that for positone problems. The difficulty is due to the fact that in the semipositone case, solutions have to live in regions where the nonlinear term is negative as well as positive. However, many methods have been applied to deal with semipositone problems, the usual approaches are quadrature method, fixed point theory, subsuper solutions method, and degree theory. We refer the readers to the survey papers [7, 8] and references therein.
Due to its importance, in recent years, continuous semipositone problems have been widely studied by many authors, see [9–15]. However, we noticed that there were only a few papers on discrete semipositone problems. One can refer to [16–18]. In these papers, semipositone discrete boundary value problems with one parameter were discussed, and subsuper solutions method and fixed point theory were used to study them. To the authors' best knowledge, there are no results established on semipositone discrete boundary value problems with two parameters. Here we want to present a different approach to deal with this topic. In [11], Costa et al. applied the nonsmooth critical point theory developed by Chang [19] to study the existence and multiplicity results of a class of semipositone boundary value problems with one parameter. We think it is also an efficient tool in dealing with the semipositone discrete boundary value problems with two parameters.
Our main objective in this paper is to apply the nonsmooth critical point theory to deal with the positive solutions of semipositone problem (1.1). More precisely, we define the discontinuous nonlinear terms

Now we consider the slightly modified problem

Just to be on the convenient side, we define  ,
,  ,
,  ,
,  , where
, where  ,
,  ,
,

We will prove in Section 3 that the sets of positive solutions of (1.1) and (1.3) do coincide. Moreover, any nonzero solution of (1.3) is nonnegative.
Our main results are as follows.
Theorem 1.1.
Suppose that there are constants  ,
,  , and
, and  such that when
such that when  is large enough,
is large enough,



Then for fixed  , there is a
, there is a  such that for
such that for  , problem (1.3) has a nontrivial nonnegative solution. Hence problem (1.1) has a positive solution.
, problem (1.3) has a nontrivial nonnegative solution. Hence problem (1.1) has a positive solution.
Remark 1.2.
By (1.6), there are constants  such that for any
such that for any  ,
,

Equations (1.6) and (1.8) imply that

which shows that  is superlinear at infinity.
is superlinear at infinity.
Remark 1.3.
Equation (1.7) implies that  is sublinear at infinity. Moreover, it is easy to know that
is sublinear at infinity. Moreover, it is easy to know that

Hence  is subquadratic at infinity.
is subquadratic at infinity.
Theorem 1.4.
Suppose that the conditions of Theorem 1.1 hold. Moreover,  is increasing on
is increasing on  . Then there is a
. Then there is a  such that for
such that for  , problem (1.1) has at least two positive solutions for sufficiently small
, problem (1.1) has at least two positive solutions for sufficiently small  .
.
Theorem 1.5.
Suppose that the conditions of Theorem 1.1 hold. Moreover,  is nondecreasing on
is nondecreasing on  . Then for fixed
. Then for fixed  , problem (1.1) has no positive solution for sufficiently large
, problem (1.1) has no positive solution for sufficiently large  .
.
2. Preliminaries
In this section, we recall some basic results on variational method for locally Lipschitz functional  defined on a real Banach space
defined on a real Banach space  with norm
with norm  .
.  is called locally Lipschitzian if for each
is called locally Lipschitzian if for each  , there is a neighborhood
, there is a neighborhood  of
of  and a constant
and a constant  such that
such that

The following abstract theory has been developed by Chang [19].
Definition 2.1.
For given  , the generalized directional derivative of the functional
, the generalized directional derivative of the functional  at
at  in the direction
in the direction  is defined by
is defined by

The following properties are known:
-
(i)
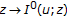 is subadditive, positively homogeneous, continuous, and convex;
is subadditive, positively homogeneous, continuous, and convex; -
(ii)
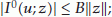
-
(iii)
 .
.
Definition 2.2.
The generalized gradient of  at
at  , denoted by
, denoted by  , is defined to be the subdifferential of the convex function
, is defined to be the subdifferential of the convex function  at
at  , that is,
, that is,

The generalized gradient  has the following main properties.
has the following main properties.
-
(1)
For all
 ,
,  is a nonempty convex and
is a nonempty convex and 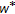 -compact subset of
-compact subset of 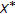 ;
; -
(2)
 for all
for all 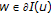 .
. -
(3)
If
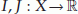 are locally Lipschitz functional, then
are locally Lipschitz functional, then 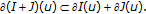 (2.4)
(2.4)
-
(4)
For any
 ,
, 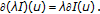
-
(5)
If
 is a convex functional, then
is a convex functional, then 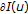 coincides with the usual subdifferential of
coincides with the usual subdifferential of 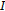 in the sense of convex analysis.
in the sense of convex analysis. -
(6)
If
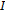 is Gâteaux differential at every point of
is Gâteaux differential at every point of  of a neighborhood
of a neighborhood  of
of  and the Gâteaux derivative is continuous, then
and the Gâteaux derivative is continuous, then 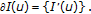
-
(7)
The function
 (2.5)
(2.5)exists, that is, there is a
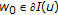 such that
such that 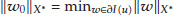 .
. -
(8)
 .
. -
(9)
If
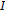 has a minimum at
has a minimum at  , then
, then 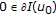 .
.
Definition 2.3.
 is a critical point of the locally Lipschitz functional
is a critical point of the locally Lipschitz functional  if
if  .
.
Definition 2.4.
 is said to satisfy Palais-Smale condition (PS) condition for short) if any sequence
is said to satisfy Palais-Smale condition (PS) condition for short) if any sequence  such that
such that  is bounded and
is bounded and  has a convergent subsequence.
has a convergent subsequence.
Lemma 2.5 (see [19, Mountain Pass Theorem]).
Let  be a real Hilbert space and let
be a real Hilbert space and let  be a locally Lipschitz functional satisfying (PS) condition. Suppose that
be a locally Lipschitz functional satisfying (PS) condition. Suppose that  and that the following hold.
and that the following hold.
-
(i)
There exist constants
 and
and  such that
such that 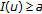 if
if 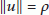 .
. -
(ii)
There is an
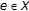 such that
such that  and
and  .
.
Then  possesses a critical value
possesses a critical value  . Moreover,
. Moreover,  can be characterized as
can be characterized as

where

Next we give the definitions of the subsolution and the supersolution of the following boundary value problem:

Definition 2.6.
If  satisfies the following conditions:
satisfies the following conditions:

then  is called a subsolution of problem (2.8).
is called a subsolution of problem (2.8).
Definition 2.7.
If  satisfies the following conditions:
satisfies the following conditions:

then  is called a supersolution of problem (2.8).
is called a supersolution of problem (2.8).
Lemma 2.8.
Suppose that there exist a subsolution  and a supersolution
and a supersolution  of problem (2.8) such that
of problem (2.8) such that  in
in  . Then there is a solution
. Then there is a solution  of problem (2.8) such that
of problem (2.8) such that  in
in  .
.
Remark 2.9.
If (2.8) is replaced by (1.1), then we have similar definitions and results as Definitions 2.6, 2.7, and Lemma 2.8
3. Proof of Main Results
Let  be the class of the functions
be the class of the functions  such that
such that  . Equipped with the usual inner product and the usual norm
. Equipped with the usual inner product and the usual norm

 is an
is an  -dimensional Hilbert space. Define the functional
-dimensional Hilbert space. Define the functional  on
on  as
as

where  ,
,  and
and

Clearly,  is a locally Lipschitz function and
is a locally Lipschitz function and  is a locally Lipschitz functional on
is a locally Lipschitz functional on  . By a simple computation, we obtain
. By a simple computation, we obtain

By [19, Theorem 2.2], the critical point of the functional  is a solution of the inclusion
is a solution of the inclusion

where  .
.
Remark 3.1.
We can show that  for
for  ,
,  for
for  . For fixed
. For fixed  and sufficiently small
and sufficiently small  ,
,  . Then
. Then  .
.
Remark 3.2.
If  , then the above inclusion becomes
, then the above inclusion becomes

It is clear that  is a positive definite matrix. Let
is a positive definite matrix. Let  be the largest and smallest eigenvalue of
be the largest and smallest eigenvalue of  , respectively. Denote by
, respectively. Denote by  . Let
. Let  . Notice that
. Notice that  for
for  and
and  for
for  . Then
. Then

Similarly,  for
for  . Hence
. Hence

Lemma 3.3.
If u is a solution of (1.3), then  . Moreover, either
. Moreover, either  in
in  , or
, or  everywhere.
everywhere.
Proof.
It is not difficult to see that  for
for  . In fact, no matter that
. In fact, no matter that  or
or  , the former inequality holds. Hence
, the former inequality holds. Hence  .
.
If  is a solution of (1.3), then we have
is a solution of (1.3), then we have

So  . Hence
. Hence  . If
. If  , then
, then

Therefore  . It follows that
. It follows that  everywhere.
everywhere.
Lemma 3.4.
If (1.6) and (1.7) hold, then  for large
for large  , where
, where  .
.
Proof.
Notice that  is equivalent to
is equivalent to  if
if  . To prove that
. To prove that  for large
for large  , it suffices to show that
, it suffices to show that

By (1.6), for large  , we have
, we have

Hence, if  is large, then
is large, then

Taking inferior limit on both sides of the above inequality, we have

Since  is superlinear and
is superlinear and  is sublinear,
is sublinear,  . Then
. Then  . Moreover, since
. Moreover, since  is subquadratic and
is subquadratic and  is superlinear,
is superlinear,  . Therefore,
. Therefore,  . From the above results, we can conclude that
. From the above results, we can conclude that  .
.
Lemma 3.5.
If (1.6) and (1.7) hold, then  satisfies (PS) condition.
satisfies (PS) condition.
Proof.
Notice that  . Let
. Let  . From [19, Theorem 2.2], for any given
. From [19, Theorem 2.2], for any given  , we have
, we have  . Then
. Then

Therefore

By Lemma 3.4, there is a constant  such that
such that  for
for  . Suppose that
. Suppose that  is a sequence such that
is a sequence such that  is bounded and
is bounded and  as
as  . Then by Properties (3) and (7) in Definition 2.2, there are
. Then by Properties (3) and (7) in Definition 2.2, there are  and
and  such that
such that  and
and

It implies that

Hence

This implies that  is bounded. Since
is bounded. Since  is finite dimensional,
is finite dimensional,  has a convergent subsequence in
has a convergent subsequence in  .□
.□
Lemma 3.6.
For fixed  , there exist
, there exist  and
and  such that if
such that if  , then
, then  for
for  .
.
Proof.
By (1.5) and (1.7), there are  such that
such that


The equivalence of norm on  implies that there exists
implies that there exists  such that
such that  , where
, where  . Let
. Let  and
and  . Let
. Let  . It follows from (3.20) and (3.21) that there is
. It follows from (3.20) and (3.21) that there is  such that if
such that if  , then
, then

Lemma 3.7.
There is an  such that
such that  and
and  .
.
Proof.
It follows from Remark 1.2 that  for
for  . By the equivalence of the norms on
. By the equivalence of the norms on  , there exists
, there exists  such that
such that  , where
, where  . Let
. Let  be the eigenfunction to the principal eigenvalue
be the eigenfunction to the principal eigenvalue  of
of

with  and
and  . Let
. Let

Clearly  . Since
. Since  , for
, for  ,
,

Hence there is a  such that
such that  . Let
. Let  . Then
. Then  and
and  . The second condition of Mountain Pass theorem is verified.□
. The second condition of Mountain Pass theorem is verified.□
Proof of Theorem 1.1.
Clearly,  . Lemma 3.5 implies that
. Lemma 3.5 implies that  satisfies (PS) condition. It follows from Lemmas 3.6, 3.7, and 2.5 that
satisfies (PS) condition. It follows from Lemmas 3.6, 3.7, and 2.5 that  has a nontrivial critical point
has a nontrivial critical point  such that
such that  . By Lemma 3.3 and Remark 3.2,
. By Lemma 3.3 and Remark 3.2,  is a positive solution of (1.1). The proof is complete.□
is a positive solution of (1.1). The proof is complete.□
Proof of Theorem 1.4.
We will apply the subsuper solutions method to prove the multiplicity results.
Firstly, we will prove that there exists  such that if
such that if  , then the following boundary value problem
, then the following boundary value problem

has a positive solution  . In fact, since
. In fact, since  is increasing on
is increasing on  and eventually strictly positive,
and eventually strictly positive,  for
for  and some
and some  . Let
. Let  be the eigenfunction to the principal eigenvalue
be the eigenfunction to the principal eigenvalue  of
of

with  and
and  .
.
Notice that  and
and  (see [20]). Let
(see [20]). Let  be a constant such that
be a constant such that  . For
. For  ,
,  , we have
, we have  .
.
We will verify that  is a subsolution of (3.26) for
is a subsolution of (3.26) for  large. Notice that
large. Notice that

On the other hand, for  , we have
, we have  , which implies that
, which implies that

Then for  ,
,  . Next, for
. Next, for  , we have
, we have  for some
for some  and
and  for some
for some  . Hence
. Hence  . Since
. Since  is increasing and eventually strictly positive, there is a
is increasing and eventually strictly positive, there is a  such that if
such that if  and
and  ,
,

Hence for  ,
,  . Notice that
. Notice that  . Then
. Then  . So we have
. So we have

that is,  is a subsolution of (3.26).
is a subsolution of (3.26).
Now we look for the supersolution of (3.26). Let  be a solution of
be a solution of

Then  , where
, where

Clearly,  for
for  ,
,  . Define
. Define  , where
, where  is large enough so
is large enough so  in
in  and
and

This is possible since  is a sublinear function. So
is a sublinear function. So

which shows that  is a supersolution of (3.26). Therefore, by Lemma 2.8, there is a solution
is a supersolution of (3.26). Therefore, by Lemma 2.8, there is a solution  of (3.26) such that
of (3.26) such that  .
.
Secondly, we will prove that  is a subsolution of (1.1). Since
is a subsolution of (1.1). Since  and
and  , it follows that
, it follows that

which implies that  is a subsolution of (1.1).
is a subsolution of (1.1).
Lastly, we will look for the supersolution of (1.1) and prove the existence of positive solution of (1.1). Let  be as in (3.32). Notice that
be as in (3.32). Notice that  is sublinear. Define
is sublinear. Define  , where
, where  is independent of
is independent of  and large enough so that
and large enough so that  in
in  and
and

Let  be so small that
be so small that

Then

Hence  is a supersolution of (1.1). Thus, by Remark 2.9, problem (1.1) has a solution
is a supersolution of (1.1). Thus, by Remark 2.9, problem (1.1) has a solution  such that
such that  for
for  and
and  small, which is positive for
small, which is positive for  .
.
Now we are going to find the second positive solution of problem (1.1). Notice that  and
and  are independent of
are independent of  . Since
. Since  is positive on
is positive on  , by the definition of
, by the definition of  we have
we have  . Then for
. Then for  ,
,

where  . On the other hand, by Lemma 3.6, we can take appropriate
. On the other hand, by Lemma 3.6, we can take appropriate  such that if
such that if  , then
, then  for
for  . Hence by Theorem 1.1,
. Hence by Theorem 1.1,  . So
. So  and
and  , which shows that
, which shows that  and
and  are two different positive solutions of (1.1). The proof is complete.
are two different positive solutions of (1.1). The proof is complete.
Proof of Theorem 1.5.
Just to be on the contradiction side, let  be a positive solution of (1.1). Since
be a positive solution of (1.1). Since  is superlinear and increasing,
is superlinear and increasing,  , there are
, there are  such that for
such that for  ,
,  . Hence for
. Hence for  and
and  ,
,  , where
, where  is the same as that of the proof of Lemma 3.7. If
is the same as that of the proof of Lemma 3.7. If  is large enough, then
is large enough, then  . Therefore
. Therefore  for large
for large  and
and  . Multiplying both sides of
. Multiplying both sides of

by  and summing it from
and summing it from  to
to  , we get
, we get

Multiplying both sides of (1.1) by  and summing it from
and summing it from  to
to  , we have
, we have

It is easy to see that

Hence

For  , we obtain a contradiction. So for a given
, we obtain a contradiction. So for a given  , (1.1) has no positive solution if
, (1.1) has no positive solution if  is large. The proof is complete.□
is large. The proof is complete.□
Example 3.8.
We give an example to illustrate the result of Theorem 1.1. Let  and
and  . Clearly,
. Clearly,  and
and  satisfy the conditions of Theorem 1.1. Then problem (1.1) has at least a positive solution.
satisfy the conditions of Theorem 1.1. Then problem (1.1) has at least a positive solution.
References
Castro A, Shivaji R: Nonnegative solutions for a class of nonpositone problems. Proceedings of the Royal Society of Edinburgh. Section A 1988, 108(3-4):291-302. 10.1017/S0308210500014670
Keller HB, Cohen DS: Some positone problems suggested by nonlinear heat generation. Journal of Mathematics and Mechanics 1967, 16: 1361-1376.
Afrouzi GA, Rasouli SH:Population models involving the
 -Laplacian with indefinite weight and constant yield harvesting. Chaos, Solitons & Fractals 2007, 31(2):404-408. 10.1016/j.chaos.2005.09.067
-Laplacian with indefinite weight and constant yield harvesting. Chaos, Solitons & Fractals 2007, 31(2):404-408. 10.1016/j.chaos.2005.09.067Myerscough MR, Gray BF, Hogarth WL, Norbury J: An analysis of an ordinary differential equation model for a two-species predator-prey system with harvesting and stocking. Journal of Mathematical Biology 1992, 30(4):389-411.
Selgrade JF: Using stocking or harvesting to reverse period-doubling bifurcations in discrete population models. Journal of Difference Equations and Applications 1998, 4(2):163-183. 10.1080/10236199808808135
Yao Q:Existence of
 solutions and/or positive solutions to a semipositone elastic beam equation. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):138-150. 10.1016/j.na.2005.11.016
solutions and/or positive solutions to a semipositone elastic beam equation. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):138-150. 10.1016/j.na.2005.11.016Castro A, Maya C, Shivaji R: Nonlinear eigenvalue problems with semipositone structure. In Proceedings of the Conference on Nonlinear Differential Equations (Coral Gables, Fla, 1999), October 2000, Electronic Journal of Differential Equations Conference. Volume 5. Southwest Texas State University, San Marcos, Tex, USA; 33-49.
Lions P-L: On the existence of positive solutions of semilinear elliptic equations. SIAM Review 1982, 24(4):441-467. 10.1137/1024101
Agarwal RP, Grace SR, O'Regan D: Semipositone higher-order differential equations. Applied Mathematics Letters 2004, 17(2):201-207. 10.1016/S0893-9659(04)90033-X
Ali J, Shivaji R:On positive solutions for a class of strongly coupled
 -Laplacian systems. Proceedings of the International Conference in Honor of Jacqueline Fleckinger, June-July 2007, Toulouse, France, Electronic Journal of Differential Equations Conference 16: 29-34.
-Laplacian systems. Proceedings of the International Conference in Honor of Jacqueline Fleckinger, June-July 2007, Toulouse, France, Electronic Journal of Differential Equations Conference 16: 29-34.Costa DG, Tehrani H, Yang J: On a variational approach to existence and multiplicity results for semipositone problems. Electronic Journal of Differential Equations 2006, 2006(11):1-10.
Dancer EN, Zhang Z:Critical point, anti-maximum principle and semipositone
 -Laplacian problems. Discrete and Continuous Dynamical Systems 2005, (supplement):209-215.
-Laplacian problems. Discrete and Continuous Dynamical Systems 2005, (supplement):209-215.Hai DD, Shivaji R:An existence result on positive solutions for a class of
 -Laplacian systems. Nonlinear Analysis: Theory, Methods & Applications 2004, 56(7):1007-1010. 10.1016/j.na.2003.10.024
-Laplacian systems. Nonlinear Analysis: Theory, Methods & Applications 2004, 56(7):1007-1010. 10.1016/j.na.2003.10.024Hai DD, Shivaji R: Uniqueness of positive solutions for a class of semipositone elliptic systems. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(2):396-402. 10.1016/j.na.2005.11.034
Yebari N, Zertiti A: Existence of non-negative solutions for nonlinear equations in the semi-positone case. In Proceedings of the Oujda International Conference on Nonlinear Analysis (Oujda 2005), 2006, San Marcos, Tex, USA, Electronic Journal of Differential Equations Conference. Volume 14. Southwest Texas State University; 249-254.
Agarwal RP, O'Regan D: Nonpositone discrete boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2000, 39(2):207-215. 10.1016/S0362-546X(98)00183-7
Agarwal RP, Grace SR, O'Regan D: Discrete semipositone higher-order equations. Computers & Mathematics with Applications 2003, 45(6–9):1171-1179.
Jiang D, Zhang L, O'Regan D, Agarwal RP: Existence theory for single and multiple solutions to semipositone discrete Dirichlet boundary value problems with singular dependent nonlinearities. Journal of Applied Mathematics and Stochastic Analysis 2003, 16(1):19-31. 10.1155/S1048953303000029
Chang K-C: Variational methods for non-differentiable functionals and their applications to partial differential equations. Journal of Mathematical Analysis and Applications 1981, 80(1):102-129. 10.1016/0022-247X(81)90095-0
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Application, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Acknowledgments
The authors would like to thank the referees for valuable suggestions. This project is supported by National Natural Science Foundation of China (no. 10625104) and Research Fund for the Doctoral Program of Higher Education of China (Grant no. 20061078002).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, J., Zhu, B. & Guo, Z. Positive Solutions for Multiparameter Semipositone Discrete Boundary Value Problems via Variational Method. Adv Differ Equ 2008, 840458 (2008). https://doi.org/10.1155/2008/840458
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/840458
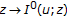 is subadditive, positively homogeneous, continuous, and convex;
is subadditive, positively homogeneous, continuous, and convex;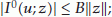
 .
. ,
,  is a nonempty convex and
is a nonempty convex and 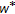 -compact subset of
-compact subset of 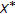 ;
; for all
for all 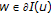 .
.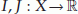 are locally Lipschitz functional, then
are locally Lipschitz functional, then 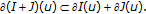
 ,
, 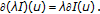
 is a convex functional, then
is a convex functional, then 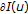 coincides with the usual subdifferential of
coincides with the usual subdifferential of 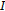 in the sense of convex analysis.
in the sense of convex analysis.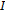 is Gâteaux differential at every point of
is Gâteaux differential at every point of  of a neighborhood
of a neighborhood  of
of  and the Gâteaux derivative is continuous, then
and the Gâteaux derivative is continuous, then 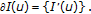

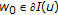 such that
such that 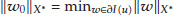 .
. .
.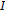 has a minimum at
has a minimum at  , then
, then 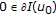 .
. and
and  such that
such that 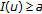 if
if 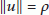 .
.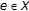 such that
such that  and
and  .
. -Laplacian with indefinite weight and constant yield harvesting. Chaos, Solitons & Fractals 2007, 31(2):404-408. 10.1016/j.chaos.2005.09.067
-Laplacian with indefinite weight and constant yield harvesting. Chaos, Solitons & Fractals 2007, 31(2):404-408. 10.1016/j.chaos.2005.09.067 solutions and/or positive solutions to a semipositone elastic beam equation. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):138-150. 10.1016/j.na.2005.11.016
solutions and/or positive solutions to a semipositone elastic beam equation. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):138-150. 10.1016/j.na.2005.11.016 -Laplacian systems. Proceedings of the International Conference in Honor of Jacqueline Fleckinger, June-July 2007, Toulouse, France, Electronic Journal of Differential Equations Conference 16: 29-34.
-Laplacian systems. Proceedings of the International Conference in Honor of Jacqueline Fleckinger, June-July 2007, Toulouse, France, Electronic Journal of Differential Equations Conference 16: 29-34. -Laplacian problems. Discrete and Continuous Dynamical Systems 2005, (supplement):209-215.
-Laplacian problems. Discrete and Continuous Dynamical Systems 2005, (supplement):209-215. -Laplacian systems. Nonlinear Analysis: Theory, Methods & Applications 2004, 56(7):1007-1010. 10.1016/j.na.2003.10.024
-Laplacian systems. Nonlinear Analysis: Theory, Methods & Applications 2004, 56(7):1007-1010. 10.1016/j.na.2003.10.024