- Research Article
- Open access
- Published:
Solutions of 2 th-Order Boundary Value Problem for Difference Equation via Variational Method
th-Order Boundary Value Problem for Difference Equation via Variational Method
Advances in Difference Equations volume 2009, Article number: 730484 (2009)
Abstract
The variational method and critical point theory are employed to investigate the existence of solutions for 2 th-order difference equation
th-order difference equation  for
for  with boundary value condition
with boundary value condition 
 by constructing a functional, which transforms the existence of solutions of the boundary value problem (BVP) to the existence of critical points for the functional. Some criteria for the existence of at least one solution and two solutions are established which is the generalization for BVP of the even-order difference equations.
by constructing a functional, which transforms the existence of solutions of the boundary value problem (BVP) to the existence of critical points for the functional. Some criteria for the existence of at least one solution and two solutions are established which is the generalization for BVP of the even-order difference equations.
1. Introduction
Difference equations have been applied as models in vast areas such as finance insurance, biological populations, disease control, genetic study, physical field, and computer application technology. Because of their importance, many literature deals with its existence and uniqueness problems. For example, see [1–10].
We notice that the existing results are usually obtained by various analytical techniques, for example, the conical shell fixed point theorem [1, 6], Banach contraction map method [7], Leray-Schauder fixed point theorem [2, 10], and the upper and lower solution method [3]. It seems that the variational technique combining with the critical point theory [11] developed in the recent decades is one of the effective ways to study the boundary value problems of difference equations. However because the variational method requires a "symmetrical'' functional, it is hard for the odd-order difference equations to create a functional satisfying the "symmetrical'' property. Therefore, the even-order difference equations have been investigated in most references.
Let  ,
,  be integers, and
be integers, and  ,
,  be a discrete interval in
be a discrete interval in  . Inspired by [5, 8], in this paper, we try to investigate the following
. Inspired by [5, 8], in this paper, we try to investigate the following  th-order boundary value problem (BVP) of difference equation via variational method combining with some traditional analytical skills:
th-order boundary value problem (BVP) of difference equation via variational method combining with some traditional analytical skills:


where  is the forward difference operator;
is the forward difference operator;  for
for  and
and  A variational functional for BVP (1.1)-(1.2) is constructed which transforms the existence of solutions of the boundary value problem (BVP) to the existence of critical points of this functional. In order to prove the existence criteria of critical points of the functional, some lemmas are given in Section 2. Two criteria for the existence of at least one solution and two solutions for BVP (1.1)-(1.2) are established in Section 3 which is the generalization for BVP of the even-order difference equations. The existence results obtained in this paper are not found in the references, to the best of our knowledge.
A variational functional for BVP (1.1)-(1.2) is constructed which transforms the existence of solutions of the boundary value problem (BVP) to the existence of critical points of this functional. In order to prove the existence criteria of critical points of the functional, some lemmas are given in Section 2. Two criteria for the existence of at least one solution and two solutions for BVP (1.1)-(1.2) are established in Section 3 which is the generalization for BVP of the even-order difference equations. The existence results obtained in this paper are not found in the references, to the best of our knowledge.
For convenience, we will use the following notations in the following sections:

2. Variational Structure and Preliminaries
We need two lemmas from [12] or [11].
Lemma 2.1.
Let  be a real reflexive Banach space with a norm
be a real reflexive Banach space with a norm  , and let
, and let  be a weakly lower (upper) semicontinuous functional, such that
be a weakly lower (upper) semicontinuous functional, such that

then there exists  such that
such that

Furthermore, if  has bounded linear Gâteaux derivative, then
has bounded linear Gâteaux derivative, then 
Lemma 2.2 (mountain-pass lemma).
Let  be a real Banach space, and let
be a real Banach space, and let  be continuously differential, satisfying the P-S condition. Assume that
be continuously differential, satisfying the P-S condition. Assume that  and
and  is an open neighborhood of
is an open neighborhood of  , but
, but  If
If  then
then  is the critical value of
is the critical value of  where
where

This means that there exists  , s.t.
, s.t.  ,
, 
The following lemma will be used in the proof of Lemma 2.4.
Lemma 2.3.
If  is a symmetric and positive-defined real matrix,
is a symmetric and positive-defined real matrix,  is a real matrix,
is a real matrix,  is the transposed matrix of
is the transposed matrix of  Then
Then  is positive defined if and only if
is positive defined if and only if 
Proof.
Since  is positive defined, then
is positive defined, then

Let  be a Hilbert space defined by
be a Hilbert space defined by

with the norm

Hence  is an
is an  -dimensional Hilbert space. For any
-dimensional Hilbert space. For any  , let
, let  then one can show that there exist constants
then one can show that there exist constants  s.t.
s.t.  ; that is,
; that is,  is an equivalent norm of
is an equivalent norm of  (see [9, page 68]).
(see [9, page 68]).
Lemma 2.4.
There is

Proof.
Since  ,
,  ,
,  By using the inequality
By using the inequality  ,
,  , we have
, we have

Repeating the above process, we obtain

On the other hand, define  ,
,  where
where  is the combination number, then we can rewrite
is the combination number, then we can rewrite  in a vector form, that is,
in a vector form, that is,  where
where  ,
,  , and
, and

where  Hence
Hence  Note that
Note that

and by Lemma 2.3 with  , we know that
, we know that  is positive defined. Hence all eigenvalues of
is positive defined. Hence all eigenvalues of  are real and positive. Let
are real and positive. Let  be the minimal eigenvalue of these
be the minimal eigenvalue of these  eigenvalues, then
eigenvalues, then  Therefore
Therefore  that is,
that is, 
However, how to find the  in Lemma 2.4 is a skillful and challenging task. The following lemma from [13] offers some help for the estimation of
in Lemma 2.4 is a skillful and challenging task. The following lemma from [13] offers some help for the estimation of  .
.
Lemma 2.5 (Brualdi [13]).
If  is weak irreducible, then each eigenvalue is contained in the set
is weak irreducible, then each eigenvalue is contained in the set

In Lemma 2.5,  is the complex number set, and the denotations
is the complex number set, and the denotations  ,
,  ,
,  ,
,  can be found in [13]. Since
can be found in [13]. Since  is positive defined, all eigenvalues are positive real numbers. Therefore, by Lemma 2.5, let
is positive defined, all eigenvalues are positive real numbers. Therefore, by Lemma 2.5, let

where  .
.  is a subset of
is a subset of  and can be calculated directly from
and can be calculated directly from  Define
Define  If
If  , we can use this
, we can use this  as
as  in Lemma 2.4. If
in Lemma 2.4. If  , then one needs to calculate the eigenvalues directly.
, then one needs to calculate the eigenvalues directly.
Define the functional  on
on  by
by

Then  is
is  with
with

where  and
and  is the inner product in
is the inner product in  . In fact, we have
. In fact, we have

The continuity of  and the right-hand side of the inequality in Lemma 2.4 lead to (2.15).
and the right-hand side of the inequality in Lemma 2.4 lead to (2.15).
Furthermore, for any  we have
we have  ,
,  By using the following formula (e.g., see [14, page 28]):
By using the following formula (e.g., see [14, page 28]):

we have

Repeating the above process, we obtain

Let  , that is,
, that is,

Since  is arbitrary, we know that the solution of BVP (1.1)-(1.2) corresponds to the critical point of
is arbitrary, we know that the solution of BVP (1.1)-(1.2) corresponds to the critical point of 
3. Main Results
Now we present our main results of this paper.
Theorem 3.1.
If there exist  ,
,  ,
,  , and
, and  s.t.
s.t.

then BVP (1.1)-(1.2) has at least one solution.
Proof.
In fact, we can choose a suitable  such that
such that

Since there exists  with
with  we have
we have

Then by Lemma 2.4, we obtain

Noticing that  we have
we have  From Lemma 2.1, the conclusion of this lemma follows.
From Lemma 2.1, the conclusion of this lemma follows.
Corollary 3.2.
If there exists  s.t.
s.t.  for all
for all  , and
, and

where  ,
,  satisfy either
satisfy either  ,
,  or
or 
 , then BVP (1.1)-(1.2) has at least one solution.
, then BVP (1.1)-(1.2) has at least one solution.
Proof.
Assume that  ,
,  Then for
Then for  there exists
there exists  such that
such that  as
as  . We have from the continuity of
. We have from the continuity of  that there is a
that there is a  such that
such that  for all
for all  ,
,  . When
. When  , one has
, one has  for
for  then
then

when  , one has
, one has  for
for  then
then

Let  , then we have
, then we have  for
for  Therefore, we have
Therefore, we have

which implies  and by Lemma 2.1, the conclusion of this lemma follows.
and by Lemma 2.1, the conclusion of this lemma follows.
Assume that  ,
,  Then for
Then for  there exists
there exists  such that
such that  as
as  . We have from the continuity of
. We have from the continuity of  that there is a
that there is a  such that
such that  for all
for all  ,
,  . When
. When  , one has
, one has  ,
,  then we have
then we have

when  , one has
, one has  ,
,  then we have
then we have

Let  , then we have
, then we have  for
for  Therefore, by Theorem 3.1, the conclusion of this lemma follows.
Therefore, by Theorem 3.1, the conclusion of this lemma follows.
Theorem 3.3.
Assume that  ,
,  and
and
-
(i)
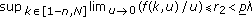 ,
, 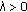 is defined in Lemma 2.4;
is defined in Lemma 2.4; -
(ii)
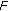 satisfies (3.1) in Theorem 3.1 or
satisfies (3.1) in Theorem 3.1 or 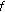 satisfies the assumptions in Corollary 3.2.
satisfies the assumptions in Corollary 3.2.
Then BVP (1.1)-(1.2) has at least two solutions.
Proof.
We first show that  satisfies the P-S condition. Let
satisfies the P-S condition. Let  satisfy that
satisfy that  is bounded and
is bounded and  If
If  is unbounded, it possesses a divergent subseries, say
is unbounded, it possesses a divergent subseries, say  as
as  . However from (ii), we get (3.4) or (3.8), hence
. However from (ii), we get (3.4) or (3.8), hence  as
as  , which is contradictory to the the fact that
, which is contradictory to the the fact that  is bounded.
is bounded.
Next we use the mountain-pass lemma to finish the proof. By (i), for  , there exists
, there exists  such that
such that  for
for  . Then
. Then  for
for  . Now together with Lemma 2.3
. Now together with Lemma 2.3 we have
we have

which implies that

where  is the zero element in
is the zero element in  , and
, and  Since we have from (3.4) or (3.8) that
Since we have from (3.4) or (3.8) that  there exists
there exists  with
with  that is,
that is,  but
but  Using Lemma 2.2, we have shown that
Using Lemma 2.2, we have shown that  is the critical value of
is the critical value of  with
with  defined as
defined as

We denote  as its corresponding critical point.
as its corresponding critical point.
On the other hand, by Theorem 3.1 or Corollary 3.2, we know that there exists  s.t.
s.t.  If
If  the theorem is proved. If on the contrary,
the theorem is proved. If on the contrary,  , that is,
, that is,  that implies for any
that implies for any  ,
,  Taking
Taking  in
in  with
with  , by the continuity of
, by the continuity of  there exist
there exist  s.t.
s.t.  ,
,  Hence
Hence  ,
,  are two different critical points of
are two different critical points of  that is, BVP (1.1)-(1.2) has at least two different solutions.
that is, BVP (1.1)-(1.2) has at least two different solutions.
4. An Example
Consider the 6th-order boundary value problem for difference equation

Let  , we have
, we have  ,
,  Hence
Hence  satisfies the conditions in Theorem 3.3, the boundary value problem (4.1) has at least two solutions.
satisfies the conditions in Theorem 3.3, the boundary value problem (4.1) has at least two solutions.
References
Agarwal RP, Henderson J: Positive solutions and nonlinear eigenvalue problems for third-order difference equations. Computers & Mathematics with Applications 1998,36(10–12):347-355.
Agarwal RP, O'Regan D:Singular discrete
 boundary value problems. Applied Mathematics Letters 1999,12(8):113-119. 10.1016/S0893-9659(99)00131-7
boundary value problems. Applied Mathematics Letters 1999,12(8):113-119. 10.1016/S0893-9659(99)00131-7Agarwal RP, Wong F-H: Upper and lower solutions method for higher-order discrete boundary value problems. Mathematical Inequalities & Applications 1998,1(4):551-557.
Agarwal RP, Perera K, O'Regan D: Multiple positive solutions of singular and nonsingular discrete problems via variational methods. Nonlinear Analysis: Theory, Methods & Applications 2004,58(1-2):69-73. 10.1016/j.na.2003.11.012
Guo ZM, Yu JS: Existence of periodic and subharmonic solutions for two-order superlinear difference equations. Science in China Series A 2003, 33: 226-235.
Jiang D, Chu J, O'Regan D, Agarwal RP:Positive solutions for continuous and discrete boundary value problems to the one-dimension
 -Laplacian. Mathematical Inequalities & Applications 2004,7(4):523-534.
-Laplacian. Mathematical Inequalities & Applications 2004,7(4):523-534.Li LT, Weng PX: Boundary value problems of second order functional difference equation. Journal of South China Normal University Natural Science Edition 2003, (3):20-24.
Liang HH, Weng PX: Existence and multiple solutions for a second-order difference boundary value problem via critical point theory. Journal of Mathematical Analysis and Applications 2007,326(1):511-520. 10.1016/j.jmaa.2006.03.017
Liang HH, Weng PX: Existence of solutions for a fourth-order difference boundary value problem and a critical point method. Applied Mathematics A Journal of Chinese Universities, Series A 2008,23(1):67-72.
Wong PJY, Agarwal RP:Existence theorems for a system of difference equations with
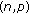 -type conditions. Applied Mathematics and Computation 2001,123(3):389-407. 10.1016/S0096-3003(00)00078-3
-type conditions. Applied Mathematics and Computation 2001,123(3):389-407. 10.1016/S0096-3003(00)00078-3Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations. Volume 65. American Mathematical Society, Providence, RI, USA; 1986:viii+100.
Ambrosetti A, Rabinowitz PH: Dual variational methods in critical point theory and applications. Journal of Functional Analysis 1973, 14: 349-381. 10.1016/0022-1236(73)90051-7
Horn RA, Johnson CR: Matrix Analysis. Cambridge University Press, Cambridge, UK; 1985:xiii+561.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Acknowledgments
This research is partially supported by the NSF of China and NSF of Guangdong Province.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zou, Q., Weng, P. Solutions of 2 th-Order Boundary Value Problem for Difference Equation via Variational Method.
Adv Differ Equ 2009, 730484 (2009). https://doi.org/10.1155/2009/730484
th-Order Boundary Value Problem for Difference Equation via Variational Method.
Adv Differ Equ 2009, 730484 (2009). https://doi.org/10.1155/2009/730484
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/730484
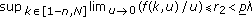 ,
, 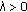 is defined in Lemma 2.4;
is defined in Lemma 2.4;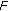 satisfies (3.1) in Theorem 3.1 or
satisfies (3.1) in Theorem 3.1 or 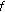 satisfies the assumptions in Corollary 3.2.
satisfies the assumptions in Corollary 3.2. boundary value problems. Applied Mathematics Letters 1999,12(8):113-119. 10.1016/S0893-9659(99)00131-7
boundary value problems. Applied Mathematics Letters 1999,12(8):113-119. 10.1016/S0893-9659(99)00131-7 -Laplacian. Mathematical Inequalities & Applications 2004,7(4):523-534.
-Laplacian. Mathematical Inequalities & Applications 2004,7(4):523-534.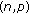 -type conditions. Applied Mathematics and Computation 2001,123(3):389-407. 10.1016/S0096-3003(00)00078-3
-type conditions. Applied Mathematics and Computation 2001,123(3):389-407. 10.1016/S0096-3003(00)00078-3