- Research Article
- Open access
- Published:
Convergence Results on a Second-Order Rational Difference Equation with Quadratic Terms
Advances in Difference Equations volume 2009, Article number: 985161 (2009)
Abstract
We investigate the global behavior of the second-order difference equation  , where initial conditions and all coefficients are positive. We find conditions on
, where initial conditions and all coefficients are positive. We find conditions on  under which the even and odd subsequences of a positive solution converge, one to zero and the other to a nonnegative number; as well as conditions where one of the subsequences diverges to infinity and the other either converges to a positive number or diverges to infinity. We also find initial conditions where the solution monotonically converges to zero and where it diverges to infinity.
under which the even and odd subsequences of a positive solution converge, one to zero and the other to a nonnegative number; as well as conditions where one of the subsequences diverges to infinity and the other either converges to a positive number or diverges to infinity. We also find initial conditions where the solution monotonically converges to zero and where it diverges to infinity.
1. Introduction and Preliminaries
There are a number of studies published on second-order rational difference equations (see, e.g., [1–9]). We investigate the global behavior of the second-order difference equation

where the numerator is quadratic and the denominator is linear with  . Under various hypotheses on the parameters, we establish the existence of different behaviors of even and odd subsequences of solutions of (1.1). Our results are summarized below.
. Under various hypotheses on the parameters, we establish the existence of different behaviors of even and odd subsequences of solutions of (1.1). Our results are summarized below.
-
(i)
Let
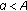 and
and 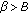 , then we have the following.
, then we have the following.-
(a)
There are infinitely many solutions,
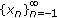 , such that for each, one of its subsequences,
, such that for each, one of its subsequences, 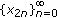 ,
, 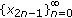 , converges to zero and the other diverges to infinity.
, converges to zero and the other diverges to infinity. -
(b)
There exist solutions,
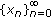 , which
, which-
(1)
converge to zero if
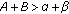 ;
; -
(2)
diverge to infinity if
 ;
; -
(3)
are constant if
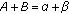 .
.
-
(1)
-
(a)
-
(i)
Let
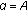 and
and 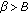 . Then for each positive solution
. Then for each positive solution  , one of the subsequences,
, one of the subsequences, 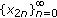 ,
, 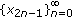 , diverges to infinity and the other to a positive number that can be arbitrarily large depending on initial values. Further there, are positive initial values for which the corresponding solution,
, diverges to infinity and the other to a positive number that can be arbitrarily large depending on initial values. Further there, are positive initial values for which the corresponding solution, 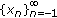 , increases monotonically to infinity.
, increases monotonically to infinity. -
(ii)
Let
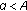 and
and 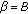 . Then for each positive solution
. Then for each positive solution 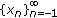 , one of the subsequences,
, one of the subsequences, 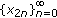 ,
, 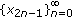 , converges to zero and the other to a nonnegative number. Further, there are positive initial values for which the corresponding solution,
, converges to zero and the other to a nonnegative number. Further, there are positive initial values for which the corresponding solution, 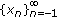 , decreases monotonically to zero.
, decreases monotonically to zero.
We note that the following results address and solve the first five conjectures posed by Sedaghat in [10].
2. Results
In order to establish this first result, we reduce (1.1) to a first-order equation by means of the substitution  This transforms (1.1) to
This transforms (1.1) to

Theorem 2.1.
Let  and
and  in (1.1). Then one has the following.
in (1.1). Then one has the following.
-
(i)
There are infinitely many solutions,
 , such that for each, one of its subsequences,
, such that for each, one of its subsequences, 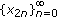 ,
,  , converges to zero and the other to infinity.
, converges to zero and the other to infinity. -
(ii)
There exist solutions,
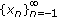 , which
, which-
(a)
converge to zero if
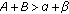 ;
; -
(b)
diverge to infinity if
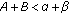 ;
; -
(c)
are constant if
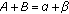 .
.
-
(a)
Proof.
Starting with (2.1), let the function  be defined as
be defined as  . Note that for
. Note that for  ,
,  is a decreasing function since
is a decreasing function since  . Also note that
. Also note that  and
and  . Hence
. Hence  has a unique positive fixed point
has a unique positive fixed point  .
.
We next compute the expression  and simplify, it including canceling the common factor
and simplify, it including canceling the common factor  from the numerator and denominator, thereby obtaining the following:
from the numerator and denominator, thereby obtaining the following:

where

Note that since  ,
,  and
and  . Thus the numerator of
. Thus the numerator of  has one and only one sign change. Therefore, by Descartes' rule of signs, the numerator of
has one and only one sign change. Therefore, by Descartes' rule of signs, the numerator of  has exactly one positive root,
has exactly one positive root,  .
.
In addition, we see that  and so, given that
and so, given that  is the only positive root of the numerator of
is the only positive root of the numerator of  , we have
, we have  for
for  . Thus, since
. Thus, since  and
and  is continuous, we must have
is continuous, we must have  for
for  . Therefore,
. Therefore,

We consider two cases depending on the initial value  for (2.1).
for (2.1).
Case 1 ( ).
).
Using induction and the fact that  is a decreasing function so that
is a decreasing function so that  is an increasing function, we have
is an increasing function, we have

Thus,  Since
Since  is the only positive fixed point of
is the only positive fixed point of  , then we must have
, then we must have  and
and 
Case 2 ( ).
).
The argument is similar to that in Case 1 in showing  and
and  In both cases, the solution,
In both cases, the solution,  , of (2.1) is divided into even and odd subsequences,
, of (2.1) is divided into even and odd subsequences,  and
and  , where one subsequence converges monotonically to zero and the other to infinity.
, where one subsequence converges monotonically to zero and the other to infinity.
We now go back to (1.1) by inferring the behavior of  from
from  . To do this we first consider
. To do this we first consider  . Without loss of generality, we will assume that
. Without loss of generality, we will assume that  and so
and so  and
and  .
.
Next, observe that

From this and our assumption with  , we have
, we have

Hence, for  , there exists
, there exists  such that
such that

for all  . We then have
. We then have

and by induction, for  ,
,

This, in turn, implies that

The argument is similar in showing that  since
since

Hence, result (i) is true.
Now consider  . Then
. Then  for all
for all  , and so
, and so  for all
for all  . Induction then gives us
. Induction then gives us  for all
for all  . We thus have one of the following:
. We thus have one of the following:
-
(1)
If
 (
(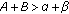 ), then
), then 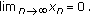
-
(2)
If
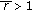 (
( ), then
), then 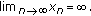
-
(3)
If
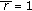 (
(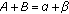 ), then
), then 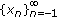 is a constant solution
is a constant solution 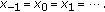
Thus the result (ii) is true and this completes the proof.
For the next couple of results we rewrite (1.1) in the form

Note that if either  and
and  , or
, or  and
and  , then
, then  satisfies the following properties:
satisfies the following properties:
-
(P1)
 , with
, with 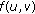 undefined when
undefined when 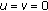 .
. -
(P2)

-
(P3)
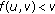 if
if 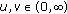 .
. -
If
we consider the addition restriction that
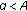 and
and 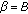 , we also obtain
, we also obtain -
(P4)
if
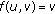 , then
, then 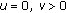 , or
, or 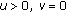 .
.
Lemma 2.2.
Let  be a positive solution of (1.1) with
be a positive solution of (1.1) with  and
and  . Then there exist
. Then there exist  and
and  such that the following statements are true:
such that the following statements are true:
-
(1)
 as
as 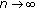 ,
, -
(2)
 as
as 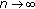 ,
, -
(3)
 , and
, and 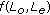 and
and 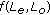 are undefined; or if either
are undefined; or if either 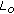 or
or  is not zero, then
is not zero, then 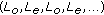 is a solution of (1.1).
is a solution of (1.1). -
(4)
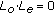 .
.
Proof.
Statements 1 and 2 follow from the fact that

by properties (P2) and (P3). Statement 3 follows from the fact that either  , and so
, and so  and
and  are undefined by property (P1); or
are undefined by property (P1); or  and
and

where Statements 1 and 2 and the continuity of  (Property (P1) hold. Finally, Statement 4 follows immediately from Statement 3 and Property (P4).
(Property (P1) hold. Finally, Statement 4 follows immediately from Statement 3 and Property (P4).
In the first three results, we characterize the convergence of the odd and even subsequences of solutions of (1.1).
Theorem 2.3.
Let  and
and  in (1.1). Then for each positive solution,
in (1.1). Then for each positive solution,  , one of the subsequences,
, one of the subsequences,  ,
,  , converges to zero and the other to a nonnegative number.
, converges to zero and the other to a nonnegative number.
Proof.
Consider (1.1) with  ,
,  , and
, and  . Then it follows from Lemma 2.2 that for each positive solution of (1.1),
. Then it follows from Lemma 2.2 that for each positive solution of (1.1),  , one of the subsequences,
, one of the subsequences,  ,
,  , converges to zero and the other to a nonnegative number.
, converges to zero and the other to a nonnegative number.
Theorem 2.4.
Let  and
and  in (1.1). Then for each positive solution
in (1.1). Then for each positive solution  , one of the subsequences,
, one of the subsequences,  ,
,  , diverges to infinity and the other to a positive number or diverges to infinity.
, diverges to infinity and the other to a positive number or diverges to infinity.
Proof.
Consider (1.1) with  and
and  . Using the transformation
. Using the transformation  convert (1.1) to the equation
convert (1.1) to the equation

Then  , and so it follows from Lemma 2.2 that for each positive solution of (2.16),
, and so it follows from Lemma 2.2 that for each positive solution of (2.16),  , one of the subsequences,
, one of the subsequences,  ,
,  , converges to zero and the other to a nonnegative number. Hence, for each positive solution of (1.1),
, converges to zero and the other to a nonnegative number. Hence, for each positive solution of (1.1),  , one of the subsequences,
, one of the subsequences,  ,
,  , diverges to infinity and the other to a positive number or diverges to infinity.
, diverges to infinity and the other to a positive number or diverges to infinity.
In the following results, we show the existence of monotonic solutions for (1.1). As with Theorem 2.1 we use the substitution 
Theorem 2.5.
Let  and
and  in (1.1). Then there are positive initial values for which the corresponding solutions,
in (1.1). Then there are positive initial values for which the corresponding solutions,  , decrease monotonically to zero.
, decrease monotonically to zero.
Proof.
Note that an equilibrium equation for (2.1) satisfies,

Set  Given Descartes' rule of signs, we have that there exists a unique positive equilibrium,
Given Descartes' rule of signs, we have that there exists a unique positive equilibrium,  , where
, where  and
and  Recall that
Recall that  and let
and let  for all
for all  . Then
. Then  for all
for all  . It follows from induction that
. It follows from induction that  for all
for all  . Since
. Since  ,
,  , with
, with  , decreases monotonically to zero.
, decreases monotonically to zero.
Theorem 2.6.
Let  and
and  in (1.1). Then there are positive initial values for which the corresponding solution,
in (1.1). Then there are positive initial values for which the corresponding solution,  , increases monotonically to infinity.
, increases monotonically to infinity.
Proof.
As in the previous proof, an equilibrium equation for (2.1) satisfies (2.17). Setting  we obtain from Descartes' rule of signs, a unique positive equilibrium,
we obtain from Descartes' rule of signs, a unique positive equilibrium,  , where
, where  and
and  Recall that
Recall that  and let
and let  for all
for all  . Then
. Then  for all
for all  . It follows from induction that
. It follows from induction that  for all
for all  . Since
. Since  ,
,  , with
, with  , increases monotonically to infinity.
, increases monotonically to infinity.
References
Amleh AM, Camouzis E, Ladas G: On second-order rational difference equation—I. Journal of Difference Equations and Applications 2007,13(11):969-1004. 10.1080/10236190701388492
Amleh AM, Camouzis E, Ladas G: On second-order rational difference equation—II. Journal of Difference Equations and Applications 2008,14(2):215-228. 10.1080/10236190701761482
Huang YS, Knopf PM: Boundedness of positive solutions of second-order rational difference equations. Journal of Difference Equations and Applications 2004,10(11):935-940. 10.1080/10236190412331285360
Kosmala WA, Kulenović MRS, Ladas G, Teixeira CT:On the recursive sequence
 . Journal of Mathematical Analysis and Applications 2000,251(2):571-586. 10.1006/jmaa.2000.7032
. Journal of Mathematical Analysis and Applications 2000,251(2):571-586. 10.1006/jmaa.2000.7032Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xii+218.
Kulenović MRS, Ladas G, Prokup NR:On the recursive sequence
 . Journal of Difference Equations and Applications 2000,6(5):563-576. 10.1080/10236190008808246
. Journal of Difference Equations and Applications 2000,6(5):563-576. 10.1080/10236190008808246Kulenović MRS, Ladas G, Sizer WS:On the recursive sequence
 . Mathematical Sciences Research Hot-Line 1998,2(5):1-16.
. Mathematical Sciences Research Hot-Line 1998,2(5):1-16.Kulenović MRS, Merino O:Global attractivity of the equilibrium of
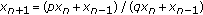 for
for  . Journal of Difference Equations and Applications 2006,12(1):101-108. 10.1080/10236190500410109
. Journal of Difference Equations and Applications 2006,12(1):101-108. 10.1080/10236190500410109Ladas G:On the recursive sequence
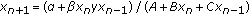 . Journal of Difference Equations and Applications 1995,1(3):317-321. 10.1080/10236199508808030
. Journal of Difference Equations and Applications 1995,1(3):317-321. 10.1080/10236199508808030Sedaghat H: Open problems and conjectures. Journal of Difference Equations and Applications 2008,14(8):889-897. 10.1080/10236190802054118
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chan, D.M., Kent, C.M. & Ortiz-Robinson, N.L. Convergence Results on a Second-Order Rational Difference Equation with Quadratic Terms. Adv Differ Equ 2009, 985161 (2009). https://doi.org/10.1155/2009/985161
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/985161
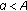 and
and 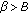 , then we have the following.
, then we have the following.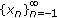 , such that for each, one of its subsequences,
, such that for each, one of its subsequences, 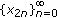 ,
, 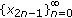 , converges to zero and the other diverges to infinity.
, converges to zero and the other diverges to infinity.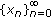 , which
, which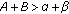 ;
; ;
;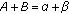 .
.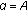 and
and 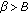 . Then for each positive solution
. Then for each positive solution  , one of the subsequences,
, one of the subsequences, 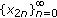 ,
, 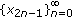 , diverges to infinity and the other to a positive number that can be arbitrarily large depending on initial values. Further there, are positive initial values for which the corresponding solution,
, diverges to infinity and the other to a positive number that can be arbitrarily large depending on initial values. Further there, are positive initial values for which the corresponding solution, 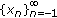 , increases monotonically to infinity.
, increases monotonically to infinity.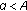 and
and 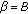 . Then for each positive solution
. Then for each positive solution 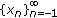 , one of the subsequences,
, one of the subsequences, 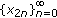 ,
, 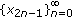 , converges to zero and the other to a nonnegative number. Further, there are positive initial values for which the corresponding solution,
, converges to zero and the other to a nonnegative number. Further, there are positive initial values for which the corresponding solution, 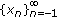 , decreases monotonically to zero.
, decreases monotonically to zero. , such that for each, one of its subsequences,
, such that for each, one of its subsequences, 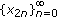 ,
,  , converges to zero and the other to infinity.
, converges to zero and the other to infinity.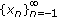 , which
, which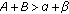 ;
;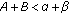 ;
;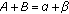 .
. (
(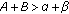 ), then
), then 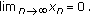
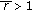 (
( ), then
), then 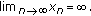
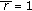 (
(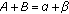 ), then
), then 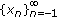 is a constant solution
is a constant solution 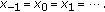
 , with
, with 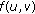 undefined when
undefined when 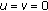 .
.
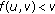 if
if 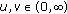 .
.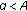 and
and 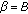 , we also obtain
, we also obtain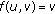 , then
, then 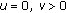 , or
, or 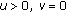 .
. as
as 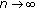 ,
, as
as 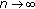 ,
, , and
, and 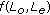 and
and 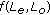 are undefined; or if either
are undefined; or if either 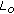 or
or  is not zero, then
is not zero, then 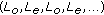 is a solution of (1.1).
is a solution of (1.1).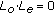 .
. . Journal of Mathematical Analysis and Applications 2000,251(2):571-586. 10.1006/jmaa.2000.7032
. Journal of Mathematical Analysis and Applications 2000,251(2):571-586. 10.1006/jmaa.2000.7032 . Journal of Difference Equations and Applications 2000,6(5):563-576. 10.1080/10236190008808246
. Journal of Difference Equations and Applications 2000,6(5):563-576. 10.1080/10236190008808246 . Mathematical Sciences Research Hot-Line 1998,2(5):1-16.
. Mathematical Sciences Research Hot-Line 1998,2(5):1-16.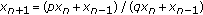 for
for  . Journal of Difference Equations and Applications 2006,12(1):101-108. 10.1080/10236190500410109
. Journal of Difference Equations and Applications 2006,12(1):101-108. 10.1080/10236190500410109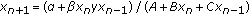 . Journal of Difference Equations and Applications 1995,1(3):317-321. 10.1080/10236199508808030
. Journal of Difference Equations and Applications 1995,1(3):317-321. 10.1080/10236199508808030