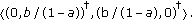- Research Article
- Open access
- Published:
Complete Asymptotic Analysis of a Nonlinear Recurrence Relation with Threshold Control
Advances in Difference Equations volume 2010, Article number: 143849 (2010)
Abstract
We consider a three-term nonlinear recurrence relation involving a nonlinear filtering function with a positive threshold  . We work out a complete asymptotic analysis for all solutions of this equation when the threshold varies from
. We work out a complete asymptotic analysis for all solutions of this equation when the threshold varies from  to
to  . It is found that all solutions either tends to 0, a limit 1-cycle, or a limit 2-cycle, depending on whether the parameter
. It is found that all solutions either tends to 0, a limit 1-cycle, or a limit 2-cycle, depending on whether the parameter  is smaller than, equal to, or greater than a critical value. It is hoped that techniques in this paper may be useful in explaining natural bifurcation phenomena and in the investigation of neural networks in which each neural unit is inherently governed by our nonlinear relation.
is smaller than, equal to, or greater than a critical value. It is hoped that techniques in this paper may be useful in explaining natural bifurcation phenomena and in the investigation of neural networks in which each neural unit is inherently governed by our nonlinear relation.
1. Introduction
Let  In [1], Zhu and Huang discussed the periodic solutions of the following difference equation:
In [1], Zhu and Huang discussed the periodic solutions of the following difference equation:

where  is a positive integer, and
is a positive integer, and  is a nonlinear signal filtering function of the form
is a nonlinear signal filtering function of the form

in which the positive number  can be regarded as a threshold parameter.
can be regarded as a threshold parameter.
In this paper, we consider the following delay difference equation:

where  and
and  . Besides the obvious and complementary differences between (1.1) and our equation, a good reason for studying (1.3) is that the study of its behavior is preparatory to better understanding of more general (neural) network models. Another one is that there are only limited materials on basic asymptotic behavior of discrete time dynamical systems with piecewise smooth nonlinearities! (Besides [1], see [2–6]. In particular, in [2], Chen considers the equation
. Besides the obvious and complementary differences between (1.1) and our equation, a good reason for studying (1.3) is that the study of its behavior is preparatory to better understanding of more general (neural) network models. Another one is that there are only limited materials on basic asymptotic behavior of discrete time dynamical systems with piecewise smooth nonlinearities! (Besides [1], see [2–6]. In particular, in [2], Chen considers the equation

where  is a nonnegative integer and
is a nonnegative integer and  is a McCulloch-Pitts type function
is a McCulloch-Pitts type function

in which  is a constant which acts as a threshold. In [3], convergence and periodicity of solutions of a discrete time network model of two neurons with Heaviside type nonlinearity are considered, while "polymodal" discrete systems in [4] are discussed in general settings.) Therefore, a complete asymptotic analysis of our equation is essential to further development of polymodal discrete time dynamical systems.
is a constant which acts as a threshold. In [3], convergence and periodicity of solutions of a discrete time network model of two neurons with Heaviside type nonlinearity are considered, while "polymodal" discrete systems in [4] are discussed in general settings.) Therefore, a complete asymptotic analysis of our equation is essential to further development of polymodal discrete time dynamical systems.
We need to be more precise about the statements to be made later. To this end, we first note that given  we may compute from (1.3) the numbers
we may compute from (1.3) the numbers  in a unique manner. The corresponding sequence
in a unique manner. The corresponding sequence  is called the solution of (1.3) determined by the initial vector
is called the solution of (1.3) determined by the initial vector  For better description of latter results, we consider initial vectors in different regions in the plane. In particular, we set
For better description of latter results, we consider initial vectors in different regions in the plane. In particular, we set

which is the complement of nonpositive orthant  and contains the positive orthant
and contains the positive orthant  Note that
Note that  is the union of the disjoint sets
is the union of the disjoint sets


Recall also that a positive integer  is a period of the sequence
is a period of the sequence  if
if  for all
for all  and that
and that  is the least or prime period of
is the least or prime period of  if
if  is the least among all periods of
is the least among all periods of  The sequence
The sequence  is said to be
is said to be  -periodic if
-periodic if  is the least period of
is the least period of  The sequence
The sequence  is said to be asymptotically periodic if there exist real numbers
is said to be asymptotically periodic if there exist real numbers  where
where  is a positive integer, such that
is a positive integer, such that

In case  is an
is an  -periodic sequence, we say that
-periodic sequence, we say that  is an asymptotically
is an asymptotically  -periodic sequence tending to the limit
-periodic sequence tending to the limit  -cycle (This term is introduced since the underlying concept is similar to that of the limit cycle in the theory of ordinary differential equations.)
-cycle (This term is introduced since the underlying concept is similar to that of the limit cycle in the theory of ordinary differential equations.)  In particular, an asymptotically
In particular, an asymptotically  -periodic sequence is a convergent sequence and conversely.
-periodic sequence is a convergent sequence and conversely.
Note that (1.3) is equivalent to the following two-dimensional autonomous dynamical system:

by means of the identification  for
for  Therefore our subsequent results can be interpreted in terms of the dynamics of plane vector sequences defined by (1.10). For the sake of simplicity, such interpretations will be left in the concluding section of this paper.
Therefore our subsequent results can be interpreted in terms of the dynamics of plane vector sequences defined by (1.10). For the sake of simplicity, such interpretations will be left in the concluding section of this paper.
To obtain complete asymptotic behavior of (1.3), we need to derive results for solutions of (1.3) determined by vectors in the entire plane. The following easy result can help us to concentrate on solutions determined by vectors in 
Theorem 1.1.
A solution  of (1.3) with
of (1.3) with  in the nonpositive orthant
in the nonpositive orthant  is nonpositive and tends to
is nonpositive and tends to 
Proof.
Let  Then by (1.3),
Then by (1.3),

and by induction, for any  we have
we have

Since  we have
we have

The proof is complete
Note that if we try to solve for an equilibrium solution  of (1.3), then
of (1.3), then

which has exactly two solutions  ,
,  when
when  and has the unique solution
and has the unique solution  when
when  However, since
However, since  is a discontinuous function, the standard theories that employ continuous arguments cannot be applied to our equilibrium solutions
is a discontinuous function, the standard theories that employ continuous arguments cannot be applied to our equilibrium solutions  or
or  to yield a set of complete asymptotic criteria. Fortunately, we may resort to elementary arguments as to be seen below.
to yield a set of complete asymptotic criteria. Fortunately, we may resort to elementary arguments as to be seen below.
To this end, we first note that our equation is autonomous (time invariant), and hence if  is a solution of (1.3), then for any
is a solution of (1.3), then for any  the sequence
the sequence  defined by
defined by  for
for  is also a solution. For the sake of convenience, we need to let
is also a solution. For the sake of convenience, we need to let

Then



We also let

Then




2. The Case 
Suppose  Then
Then

We first show the following.
Lemma 2.1.
Let  If
If  is a solution of (1.3) with
is a solution of (1.3) with  then there exists an integer
then there exists an integer  such that
such that 
Proof.
From our assumption, we have  Let
Let  be a solution of (1.3) with
be a solution of (1.3) with  Then there are eight cases.
Then there are eight cases.
Case 1.
If  our assertion is true by taking
our assertion is true by taking 
Case 2.
Suppose  Then
Then  Furthermore, in view of (1.17) and (2.1),
Furthermore, in view of (1.17) and (2.1),

If  then by (1.3),
then by (1.3),

This means that our assertion is true by taking  Next, if
Next, if  then by (1.3) and (1.18),
then by (1.3) and (1.18),

Thus our assertion holds by taking  If
If  where
where  is an arbitrary positive integer, then by (1.3),
is an arbitrary positive integer, then by (1.3),

By induction,

Thus our assertion holds by taking 
Case 3.
Suppose  We assert that there is a nonnegative integer
We assert that there is a nonnegative integer  such that
such that  for
for  and
and  Otherwise we have
Otherwise we have  for
for  It follows that
It follows that

By induction, for any  we have
we have

which implies

This is contrary to the fact that  for
for 
Now that there exists an integer  such that
such that  and
and  it then follows
it then follows

If  then our assertion holds by taking
then our assertion holds by taking  If
If  then
then  Thus
Thus

If  then our assertion holds by taking
then our assertion holds by taking  If
If  we have
we have  Hence
Hence

Repeating the procedure, we have

If  then our assertion holds by taking
then our assertion holds by taking  Otherwise,
Otherwise,

for all  But this is contrary to (2.1). Thus we conclude that
But this is contrary to (2.1). Thus we conclude that  for some
for some  Our assertion then holds by taking
Our assertion then holds by taking 
Case 4.
Suppose  As in Case 2,
As in Case 2,

If  then by (1.3),
then by (1.3),

Thus our assertion holds taking  If
If  then by (1.3),
then by (1.3),

Thus our assertion holds by taking  If
If  where
where  is an arbitrary positive integer, then by (1.3),
is an arbitrary positive integer, then by (1.3),

Thus our assertion holds by taking 
Case 5.
Suppose  Then by (1.21) and (1.23),
Then by (1.21) and (1.23),

If  then by (1.3),
then by (1.3),

Thus our assertion holds by  If
If  then by (1.3),
then by (1.3),

Thus our assertion holds by taking  If
If  where
where  is an arbitrary positive integer, then by (1.3), we have
is an arbitrary positive integer, then by (1.3), we have

That is,  Therefore we may conclude our assertion by induction.
Therefore we may conclude our assertion by induction.
Case 6.
Suppose  Since
Since

we see that

If  then by (1.3),
then by (1.3),

That is,  We may thus apply the conclusion of Case 5 and the time invariance property of (1.3) to deduce our assertion. If
We may thus apply the conclusion of Case 5 and the time invariance property of (1.3) to deduce our assertion. If  where
where  is an arbitrary nonnegative integer, then by (1.3), we have
is an arbitrary nonnegative integer, then by (1.3), we have

That is,  We may thus use induction to conclude our assertion.
We may thus use induction to conclude our assertion.
Case 7.
Suppose  As in Case 5,
As in Case 5,

If  then by (1.3),
then by (1.3),

Thus our assertion holds by taking  If
If  then by (1.3),
then by (1.3),

That is,  Thus our assertion holds by taking
Thus our assertion holds by taking 
If  where
where  is an arbitrary positive integer, then by (1.3), we have
is an arbitrary positive integer, then by (1.3), we have

That is,  Thus our assertion follows from induction.
Thus our assertion follows from induction.
Case 8.
Suppose  Then
Then

If  then by (1.3),
then by (1.3),

That is,  We may now apply the assertion in Case 5 to conclude our proof. If
We may now apply the assertion in Case 5 to conclude our proof. If  where
where  is an arbitrary nonnegative integer, then by (1.3), we have
is an arbitrary nonnegative integer, then by (1.3), we have

That is,  We may thus complete our proof by induction.
We may thus complete our proof by induction.
Theorem 2.2.
Suppose  then a solution
then a solution  of (1.3) with
of (1.3) with  will tend to
will tend to  .
.
Proof.
In view of Lemma 2.1, we may assume without loss of generality that  From our assumption, we have
From our assumption, we have  Furthermore, by (1.3),
Furthermore, by (1.3),

By induction, for any  we have
we have

and similarly

Thus  for any
for any  and
and

The proof is complete.
3. The Case 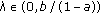
We first show that following result.
Lemma 3.1.
Let  If
If  is a solution of (1.3) with
is a solution of (1.3) with  there exists an integer
there exists an integer  such that
such that  and
and  (or
(or  and
and  ).
).
Proof.
From our assumption, we have  Let
Let  be the solution of (1.3) determined by
be the solution of (1.3) determined by  Then there are eight cases to show that there exists an integer
Then there are eight cases to show that there exists an integer  such that
such that  and
and  .
.
Case 1.
Suppose  Then our assertion is true by taking
Then our assertion is true by taking 
Case 2.
Suppose  By (1.3)
By (1.3)

This means that our assertion is true by taking 
Case 3.
Suppose  If
If  for any
for any  then by (1.3),
then by (1.3),

By induction, for any  we have
we have

Hence

But this is contrary to our assumption that  Hence there exists an integer
Hence there exists an integer  such that
such that  and
and  Thus our assertion holds by taking
Thus our assertion holds by taking 
Case 4.
Suppose  As in Case 3 of Lemma 2.1, we may show that if
As in Case 3 of Lemma 2.1, we may show that if  for all
for all  then it follows that
then it follows that

But this is contrary to the fact that  for
for  Hence there exists an integer
Hence there exists an integer  such that
such that  and
and  it then follows
it then follows

This means that our assertion is true by taking 
Case 5.
Suppose  . Then by (1.21) and (1.23),
. Then by (1.21) and (1.23),

If  then by (1.3),
then by (1.3),

When  we have
we have

That is,  We may thus apply the conclusion of Case 3 to deduce our assertion.
We may thus apply the conclusion of Case 3 to deduce our assertion.
Suppose  If
If  then we have
then we have

We may apply the conclusion of Case 3 to deduce our assertion. If  we have
we have

Thus our assertion holds by taking  If
If  then by (1.3),
then by (1.3),

That is,  In view of the above discussions, our assertion is true. If
In view of the above discussions, our assertion is true. If  where
where  is an arbitrary positive integer, then by (1.3), we have
is an arbitrary positive integer, then by (1.3), we have

That is,  Therefore we may conclude our assertion by induction.
Therefore we may conclude our assertion by induction.
Case 6.
Suppose

As in Case 6 of Lemma 2.1, if  then by (1.3), we have
then by (1.3), we have  We may thus apply the conclusion of Case 5 to deduce our assertion. If
We may thus apply the conclusion of Case 5 to deduce our assertion. If  where
where  is an arbitrary nonnegative integer, then by (1.3), we have
is an arbitrary nonnegative integer, then by (1.3), we have  We may thus use induction to conclude our assertion.
We may thus use induction to conclude our assertion.
Case 7.
Suppose  By (1.3), we have
By (1.3), we have

That is,  We may thus apply the conclusion of Case 5 to deduce our assertion.
We may thus apply the conclusion of Case 5 to deduce our assertion.
Case 8.
Suppose  Then
Then

As in Case 8 of Lemma 2.1, if  then by (1.3), we have
then by (1.3), we have  We may now apply the assertion in Case 5 to conclude our proof. If
We may now apply the assertion in Case 5 to conclude our proof. If  where
where  is an arbitrary nonnegative integer, then by (1.3), we have
is an arbitrary nonnegative integer, then by (1.3), we have  We may thus complete our proof by induction.
We may thus complete our proof by induction.
Theorem 3.2.
Let  Then any solution
Then any solution  of (1.3) with
of (1.3) with  is asymptotically
is asymptotically  -periodic with limit
-periodic with limit  -cycle
-cycle 
Proof.
In view of Lemma 3.1, we may assume without loss of generality that  and
and  Then by (1.3),
Then by (1.3),

By induction, for any  we have
we have

Thus  and
and  for any
for any  Then
Then

4. The Case 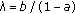
Suppose  Then
Then  We need to consider solutions with initial vectors in
We need to consider solutions with initial vectors in  or
or  defined by (1.7) and (1.8), respectively.
defined by (1.7) and (1.8), respectively.
Lemma 4.1.
Let  If
If  is a solution of (1.3) with
is a solution of (1.3) with  then there exists an integer
then there exists an integer  such that
such that 
The proof is the same as the discussions in Cases 5 through Case 8 in the proof of Lemma 2.1, and hence is skipped.
Theorem 4.2.
Suppose  then a solution
then a solution  of (1.3) with
of (1.3) with  will tend to
will tend to 
Proof.
In view of Lemma 4.1, we may assume without loss of generality that  By (1.3),
By (1.3),

By induction, for any  we have
we have

and similarly

Thus  for any
for any  Thus (2.37) hold so that
Thus (2.37) hold so that

The proof is complete.
Theorem 4.3.
Suppose  then any solution
then any solution  of (1.3) with
of (1.3) with  is asymptotically
is asymptotically  -periodic with limit
-periodic with limit  -cycle
-cycle 
Proof.
We first discuss the case, where  By (1.3),
By (1.3),

By induction, for any  we have
we have

Thus  and
and  for any
for any  Then
Then

If  then by (1.3),
then by (1.3),

That is,  We may thus apply the previous conclusion to deduce our assertion.
We may thus apply the previous conclusion to deduce our assertion.
If  then similar to the discussions of Case 3 of Lemma 2.1, there exists an integer
then similar to the discussions of Case 3 of Lemma 2.1, there exists an integer  such that
such that  and
and  That is,
That is,  In view of the previous case, our assertion holds. The proof is complete.
In view of the previous case, our assertion holds. The proof is complete.
5. Concluding Remarks
The results in the previous sections can be stated in terms of the two-dimensional dynamical system (1.10). Indeed, a solution of (1.10) is a vector sequence of the form  that renders (1.10) into an identity for each
that renders (1.10) into an identity for each  It is uniquely determined by
It is uniquely determined by 
Let us say that a solution  of (1.10) eventually falls into a plane region
of (1.10) eventually falls into a plane region  if
if  for all large
for all large  that it is eventually falls into two disjoint plane regions
that it is eventually falls into two disjoint plane regions  and
and  alternately if there is some
alternately if there is some  such that
such that  and
and  for all
for all  and that it approaches a limit
and that it approaches a limit  -cycle
-cycle  if there is some
if there is some  such that
such that  and
and  as
as  Then we may restate the previous theorems as follows.
Then we may restate the previous theorems as follows.
-
(i)
The vectors


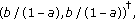 and
and 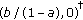 form the corners of a square in the plane.
form the corners of a square in the plane. -
(ii)
A solution
 of (1.10) with
of (1.10) with  in the nonpositive orthant
in the nonpositive orthant  (is nonpositive and) tends to
(is nonpositive and) tends to 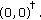
-
(iii)
Suppose
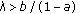 , then a solution
, then a solution  of (1.10) with
of (1.10) with  in
in  will (eventually falls into
will (eventually falls into  and) tend to
and) tend to 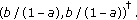
-
(iv)
Suppose
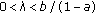 , then a solution
, then a solution 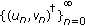 of (1.10) with
of (1.10) with  in
in  will (eventually falls into
will (eventually falls into 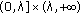 and
and  alternately and) approach the limit
alternately and) approach the limit  -cycle
-cycle 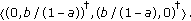
-
(v)
Suppose
 , then a solution
, then a solution 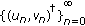 of (1.10) with
of (1.10) with  in
in 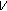 will (eventually falls into
will (eventually falls into 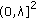 ) tend to
) tend to 
-
(vi)
Suppose
 , Then a solution
, Then a solution  of (1.10) with
of (1.10) with 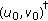 in
in  will (eventually falls into
will (eventually falls into 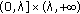 and
and 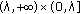 alternately) approach the limit
alternately) approach the limit  -cycle
-cycle 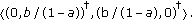
Since we have obtained a complete set of asymptotic criteria, we may deduce (bifurcation) results such as the following.
If  then all solutions
then all solutions  originated from the positive orthant approach the limit
originated from the positive orthant approach the limit  -cycle
-cycle  if
if  then all solutions originated from the positive orthant tend to
then all solutions originated from the positive orthant tend to  if
if  then all solutions originated from the positive orthant tend to
then all solutions originated from the positive orthant tend to  if
if  and approach the limit cycle
and approach the limit cycle  otherwise.
otherwise.
Roughly the above statements show that when the threshold parameter  is a relatively small positive parameter, all solutions from the positive orthant tend to a limit
is a relatively small positive parameter, all solutions from the positive orthant tend to a limit  -cycle; when it reaches the critical value
-cycle; when it reaches the critical value  some of these solutions (those from
some of these solutions (those from  ) switch away and tend to a limit
) switch away and tend to a limit  -cycle, and when
-cycle, and when  drifts beyond the critical value, all solutions tend to the limit
drifts beyond the critical value, all solutions tend to the limit  -cycle. Such an observation seems to appear in many natural processes and hence our model may be used to explain such phenomena. It is also expected that when a group of neural units interact with each other in a network where each unit is governed by evolutionary laws of the form (1.3), complex but manageable analytical results can be obtained. These will be left to other studies in the future.
-cycle. Such an observation seems to appear in many natural processes and hence our model may be used to explain such phenomena. It is also expected that when a group of neural units interact with each other in a network where each unit is governed by evolutionary laws of the form (1.3), complex but manageable analytical results can be obtained. These will be left to other studies in the future.
References
Zhu HY, Huang LH: Asymptotic behavior of solutions for a class of delay difference equation. Annals of Differential Equations 2005,21(1):99-105.
Chen Y: All solutions of a class of difference equations are truncated periodic. Applied Mathematics Letters 2002,15(8):975-979. 10.1016/S0893-9659(02)00072-1
Yuan ZH, Huang LH, Chen YM: Convergence and periodicity of solutions for a discrete-time network model of two neurons. Mathematical and Computer Modelling 2002,35(9-10):941-950. 10.1016/S0895-7177(02)00061-4
Sedaghat H: Nonlinear Difference Equations: Theory with Applications to Social Science Models, Mathematical Modelling: Theory and Applications. Volume 15. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:xvi+388.
di Bernardo M, Budd CJ, Champneys AR, Kowalczyk P: Piecewise Smooth Dynamical Systems. Springer, New York, NY, USA; 2008.
Hou CM, Cheng SS: Eventually periodic solutions for difference equations with periodic coefficients and nonlinear control functions. Discrete Dynamics in Nature and Society 2008, 2008:-21.
Acknowledgment
This project was supported by the National Natural Science Foundation of China (10661011).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ge, Q., Hou, C. & Cheng, S. Complete Asymptotic Analysis of a Nonlinear Recurrence Relation with Threshold Control. Adv Differ Equ 2010, 143849 (2010). https://doi.org/10.1155/2010/143849
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/143849

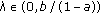
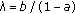


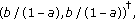 and
and 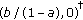 form the corners of a square in the plane.
form the corners of a square in the plane. of (1.10) with
of (1.10) with  in the nonpositive orthant
in the nonpositive orthant  (is nonpositive and) tends to
(is nonpositive and) tends to 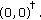
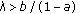 , then a solution
, then a solution  of (1.10) with
of (1.10) with  in
in  will (eventually falls into
will (eventually falls into  and) tend to
and) tend to 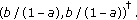
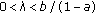 , then a solution
, then a solution 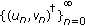 of (1.10) with
of (1.10) with  in
in  will (eventually falls into
will (eventually falls into 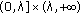 and
and  alternately and) approach the limit
alternately and) approach the limit  -cycle
-cycle 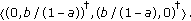
 , then a solution
, then a solution 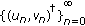 of (1.10) with
of (1.10) with  in
in 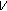 will (eventually falls into
will (eventually falls into 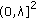 ) tend to
) tend to 
 , Then a solution
, Then a solution  of (1.10) with
of (1.10) with 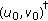 in
in  will (eventually falls into
will (eventually falls into 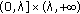 and
and 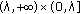 alternately) approach the limit
alternately) approach the limit  -cycle
-cycle