- Research Article
- Open access
- Published:
On Homoclinic Solutions of a Semilinear 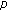 -Laplacian Difference Equation with Periodic Coefficients
-Laplacian Difference Equation with Periodic Coefficients
Advances in Difference Equations volume 2010, Article number: 195376 (2010)
Abstract
We study the existence of homoclinic solutions for semilinear  -Laplacian difference equations with periodic coefficients. The proof of the main result is based on Brezis-Nirenberg's Mountain Pass Theorem. Several examples and remarks are given.
-Laplacian difference equations with periodic coefficients. The proof of the main result is based on Brezis-Nirenberg's Mountain Pass Theorem. Several examples and remarks are given.
1. Introduction
This paper is concerned with the study of the existence of homoclinic solutions for the  -Laplacian difference equation
-Laplacian difference equation

where  is a sequence or real numbers,
is a sequence or real numbers,  is the difference operator
is the difference operator  ,
,

is referred to as the  -Laplacian difference operator, and functions
-Laplacian difference operator, and functions  and
and  are
are  -periodic in
-periodic in  and satisfy suitable conditions.
and satisfy suitable conditions.
In the theory of differential equations, a trajectory  , which is asymptotic to a constant as
, which is asymptotic to a constant as  is called doubly asymptotic or homoclinic orbit. The notion of homoclinic orbit is introduced by Poincaré [1] for continuous Hamiltonian systems.
is called doubly asymptotic or homoclinic orbit. The notion of homoclinic orbit is introduced by Poincaré [1] for continuous Hamiltonian systems.
Recently, there is a large literature on the use of variational methods to the existence of homoclinic or heteroclinic orbits of Hamiltonian systems; see [2–7] and the references therein.
In the recent paper of Li [8] a unified approach to the existence of homoclinic orbits for some classes of ODE's with periodic potentials is presented. It is based on the Brezis and Nirenberg's mountain-pass theorem [9]. In this paper we extend this approach to homoclinic orbits for discrete  -Laplacian type equations.
-Laplacian type equations.
Discrete boundary value problems have been intensively studied in the last decade. The studies of such kind of problems can be placed at the interface of certain mathematical fields, such as nonlinear differential equations and numerical analysis. On the other hand, they are strongly motivated by their applicability to mathematical physics and biology.
The variational approach to the study of various problems for difference equations has been recently applied in, among others, the papers of Agarwal et al. [10], Cabada et al. [11], Chen and Fang [12], Fang and Zhao [13], Jiang and Zhou [14], Ma and Guo [15], Mihăilescu et al. [16], Kristály et al. [17].
Along the paper, given two integer numbers  , we will denote
, we will denote  . Moreover, for every
. Moreover, for every  , we consider the following function
, we consider the following function

It is obvious that  for all
for all  and
and  . Moreover
. Moreover

Suppose that


Denote

Let us consider functions  satisfying the following assumptions.
satisfying the following assumptions.
(F1) The function  is continuous in
is continuous in  and
and  -periodic in
-periodic in  .
.
(F2) The potential function  of
of 

satisfies the Rabinowitz's type condition:
There exist  and
and  such that
such that

(F3)  as
as  .
.
Further we consider the semilinear eigenvalue  -Laplacian difference equation
-Laplacian difference equation

where  and we are looking for its homoclinic solutions, that is, solutions of (1.10) such that
and we are looking for its homoclinic solutions, that is, solutions of (1.10) such that  as
as  .
.
In order to obtain homoclinic solutions of (1.10), we will use variational approach and Brezis-Nirenberg mountain pass theorem [9].
To this end, consider the functional  , defined as
, defined as

Our main result is the following.
Theorem 1.1.
Suppose that the function  is positive and
is positive and  -periodic and the functions
-periodic and the functions  satisfy assumptions
satisfy assumptions  −
− . Then, for each
. Then, for each  , (1.10) has a nonzero homoclinic solution
, (1.10) has a nonzero homoclinic solution  , which is a critical point of the functional
, which is a critical point of the functional  .
.
Moreover, given a nontrivial solution  of problem (1.10), there exist
of problem (1.10), there exist  two integer numbers such that for all
two integer numbers such that for all  and
and  , the sequence
, the sequence  is strictly monotone.
is strictly monotone.
The paper is organized as follows. In Section 2, we present the proof of the main result and discuss the optimality of the condition  . In Section 3, we give some examples of equations modeled by this kind of problems and present some additional remarks.
. In Section 3, we give some examples of equations modeled by this kind of problems and present some additional remarks.
2. Proof of the Main Result
Let  be a sequence,
be a sequence,  and
and

It is well known that if  , then
, then  . Indeed, if
. Indeed, if  , there exists a positive integer number
, there exists a positive integer number  , such that for all
, such that for all  satisfying
satisfying  it is verified that
it is verified that  and, as consequence,
and, as consequence,  and the series
and the series  is convergent too.
is convergent too.
Consider now the functional  , defined as
, defined as

with  given in (1.7) and
given in (1.7) and  defined in (1.8).
defined in (1.8).
We have the following result.
Lemma 2.1.
The functional  is well defined,
is well defined,  -differentiable, and its critical points are solutions of (1.10).
-differentiable, and its critical points are solutions of (1.10).
Proof.
By using the inequality for nonnegative  and
and  and
and 

and the inclusion  for
for  , it follows that
, it follows that

Now, let us see that the series  is convergent: by using
is convergent: by using  , it follows that there exist
, it follows that there exist  and sufficiently large
and sufficiently large  such that
such that

Then, the series  is convergent and the functional
is convergent and the functional  is well defined on
is well defined on  .
.
It is Gâteaux differentiable and for  :
:

and partial derivatives

are continuous functions.
Moreover the functional  is continuously Fréchet-differentiable in
is continuously Fréchet-differentiable in  . It is clear, by (2.7), that the critical points of
. It is clear, by (2.7), that the critical points of  are solutions of (1.10).
are solutions of (1.10).
To obtain homoclinic solutions of (1.10) we will use mountain-pass theorem of Brezis and Nirenberg [9]. Recall its statement. Let  be a Banach space with norm
be a Banach space with norm  , and
, and  be a
be a  -functional.
-functional.  satisfies the
satisfies the  condition if every sequence
condition if every sequence  of
of  such that
such that

has a convergent subsequence. A sequence  such that (2.8) holds is referred to as
such that (2.8) holds is referred to as  -sequence.
-sequence.
Theorem 2.2 (mountain-pass theorem, Brezis and Nirenberg [9]).
Let  be a Banach space with norm
be a Banach space with norm  ,
,  and suppose that there exist
and suppose that there exist  ,
,  and
and  such that
such that 
-
(i)
 if
if  ,
, -
(ii)
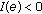 .
.
Let  , where
, where

Then, there exists a  sequence for
sequence for  . Moreover, if
. Moreover, if  satisfies the
satisfies the  condition, then
condition, then  is a critical value of
is a critical value of  , that is, there exists
, that is, there exists  such that
such that  and
and  .
.
Note that, by assumption (1.5), the norm  in
in  is equivalent to
is equivalent to

Lemma 2.3.
Suppose that  −
− hold, then there exist
hold, then there exist  ,
,  and
and  such that
such that  and
and
-
(1)
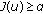 if
if  ,
, -
(2)
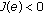 .
.
Proof.
By  , there exists
, there exists  such that
such that

Let  (
( defined in (1.6)), then, for
defined in (1.6)), then, for  ,
,  ,
,

which implies that  for all
for all  .
.
Hence, by (2.11)

By  , there exist
, there exist  ,
,  such that
such that  for all
for all  and
and  .
.
Take  ,
,  ,
,  if
if  . Then, since
. Then, since 

if  is sufficiently large.
is sufficiently large.
Then, we can take  large enough, such that for
large enough, such that for  ,
,  and (2.14) holds.
and (2.14) holds.
Lemma 2.4.
Suppose that the assumptions of Lemma 2.3 hold. Then, there exists  and a
and a  -bounded
-bounded  sequence for
sequence for  .
.
Proof.
By Lemma 2.3 and Theorem 2.2 there exists a sequence  such that
such that

where

 and
and  is defined in the proof of Lemma 2.3.
is defined in the proof of Lemma 2.3.
We will prove that the sequence  is bounded in
is bounded in  . We have for
. We have for 

and, by  ,
,

which implies that the sequence  is bounded in
is bounded in  .
.
Now we are in a position to prove Theorem 1.1.
Proof of Theorem 1.1.
For any  , the sequence
, the sequence  , given in Lemma 2.4, is bounded in
, given in Lemma 2.4, is bounded in  and, in consequence,
and, in consequence,  as
as  . Let
. Let  takes its maximum at
takes its maximum at  . There exists a unique
. There exists a unique  , such that
, such that  and let
and let  . Then
. Then  takes its maximum at
takes its maximum at  . By the
. By the  -periodicity of
-periodicity of  and
and  , it follows that
, it follows that

Since  is bounded in
is bounded in  , there exists
, there exists  , such that
, such that  weakly in
weakly in  . The weak convergence in
. The weak convergence in  implies that
implies that  for every
for every  . Indeed, if we take a test function
. Indeed, if we take a test function  ,
,  ,
,  if
if  , then
, then

Moreover, for any 

which implies that  , which means that for every
, which means that for every  ,
,

Let us take  with compact support, that is, there exist
with compact support, that is, there exist  ,
,  such that
such that  if
if  and
and  if
if  . The set of such elements
. The set of such elements  is dense in
is dense in  because if
because if  and
and  is such that
is such that  if
if  ,
,  if
if  , then
, then  as
as  . Taking
. Taking  in (2.22), due to the finite sums and the continuity of functions
in (2.22), due to the finite sums and the continuity of functions  , we obtain, passing to a limit, that
, we obtain, passing to a limit, that

From the density of  in
in  , we deduce that the previous equality is fulfilled for all
, we deduce that the previous equality is fulfilled for all  and, in consequence,
and, in consequence,  is a critical point of the functional
is a critical point of the functional  , that is,
, that is,  is a solution of (1.10).
is a solution of (1.10).
It remains to show that  .
.
Assuming, on the contrary, that  , we conclude that
, we conclude that

By  , for a given
, for a given  , there exists
, there exists  , such that if
, such that if  then, for every
then, for every  , the following inequalities holds:
, the following inequalities holds:

By (2.24), for every  , there exists a positive integer
, there exists a positive integer  such that for all
such that for all  it follows that
it follows that  . Since the maximum value of
. Since the maximum value of  is attained at
is attained at  , it follows that for
, it follows that for  and every
and every 

Then, by (2.25), for  and every
and every  :
:

which implies that

Since  is bounded in
is bounded in  ,
,  and
and  is arbitrary, by (2.28) we obtain a contradiction with
is arbitrary, by (2.28) we obtain a contradiction with  . The proof of the first part is complete.
. The proof of the first part is complete.
Now, let  be a nonzero homoclinic solution of problem (1.10). Assume that it attains positive local maximums and/or negative local minimums at infinitely many points
be a nonzero homoclinic solution of problem (1.10). Assume that it attains positive local maximums and/or negative local minimums at infinitely many points  . In particular we can assume that
. In particular we can assume that  . In consequence
. In consequence  and
and  .
.
From this, multiplying in (1.10) by  , we have
, we have

By means of condition  we arrive at the following contradiction:
we arrive at the following contradiction:

Suppose now that function  vanishes at infinitely many points
vanishes at infinitely many points  . From condition
. From condition  we conclude that
we conclude that  and, in consequence,
and, in consequence,  . Therefore it has an unbounded sequence of positive local maximums and negative local minimums, in contradiction with the previous assertion.
. Therefore it has an unbounded sequence of positive local maximums and negative local minimums, in contradiction with the previous assertion.
As a direct consequence of the two previous properties, we deduce that, for  large enough, function
large enough, function  has constant sign and it is strictly monotone.
has constant sign and it is strictly monotone.
To illustrate the optimality of the obtained results, we present in the sequel an example in which it is pointed out that condition  cannot be removed to deduce the existence result proved in Theorem 1.1.
cannot be removed to deduce the existence result proved in Theorem 1.1.
Example 2.5.
Let  be a
be a  -periodic sequence,
-periodic sequence,  ,
,  and
and  be fixed. Consider problem (1.10) with
be fixed. Consider problem (1.10) with

It is obvious that condition  holds. Since
holds. Since  we have that condition
we have that condition  is trivially fulfilled. Concerning to condition
is trivially fulfilled. Concerning to condition  , we have that
, we have that

It is clear that  for all
for all  and that
and that  for all
for all  if and only if
if and only if  .
.
When  , the inequality
, the inequality  holds if and only if either
holds if and only if either  or
or  and
and

As consequence, the inequality  for all
for all  is satisfied if and only if
is satisfied if and only if  , that is, condition
, that is, condition  does not hold.
does not hold.
Let us see that this problem has only the trivial solution for small values of the parameter  .
.
Since  , it is not difficult to verify that, for
, it is not difficult to verify that, for  , the function
, the function  is strictly decreasing for every integer
is strictly decreasing for every integer  . So, for
. So, for  in that situation, we have that
in that situation, we have that

Suppose that there is a nontrivial solution  of the considered problem, and moreover it takes some positive values. Let
of the considered problem, and moreover it takes some positive values. Let  be such that
be such that  . In such a case we deduce the following contradiction:
. In such a case we deduce the following contradiction:

Analogously it can be verified that the solution  has no negative values on
has no negative values on  .
.
3. Remarks and Examples
In this section we will consider some examples and remarks on applications and extensions of Theorem 1.1 to the existence of homoclinic solutions of difference equations of following types:
-
(A)
Second-order discrete
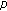 -Laplacian equations of the form
-Laplacian equations of the form 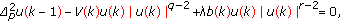 (3.1)
(3.1)
with .
.
-
(B)
Higher even-order difference equations. A model equation is the fourth-order extended Fisher-Kolmogorov equation
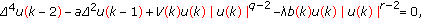 (3.2)
(3.2)
with .
.
-
(C)
Second-order difference equations with cubic and quintic nonlinearities of the forms
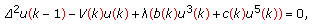 (3.3)
(3.3)

arising in mathematical physics and biology.
(A) Second-Order Discrete -Laplacian Equations.
-Laplacian Equations.
The spectrum of the Dirichlet problem  for (3.1), subject to Dirichlet boundary conditions
for (3.1), subject to Dirichlet boundary conditions

is studied in [17]. It is proved that if  ,
,  and
and  is a given function, then there exist two positive constants
is a given function, then there exist two positive constants  and
and  with
with  such that no
such that no  is an eigenvalue of problem
is an eigenvalue of problem  while any
while any  is an eigenvalue of problem
is an eigenvalue of problem  . Moreover, we have
. Moreover, we have

where  and
and  . Note that if
. Note that if  is positive and
is positive and  then
then

where  is a constant depending on
is a constant depending on  , which implies that
, which implies that  and
and  as
as  . It implies that for a given
. It implies that for a given  , there exists
, there exists  such that for any
such that for any  , the problem
, the problem  has a solution for every
has a solution for every  .
.
We extend this phenomenon, looking for homoclinic solutions of (3.1). Applying Theorem 1.1 with  and
and  , we obtain the following.
, we obtain the following.
Corollary 3.1.
Suppose that the function  is positive and
is positive and  -periodic and
-periodic and  . Then, for each
. Then, for each  , (3.1) has a nonzero homoclinic solution.
, (3.1) has a nonzero homoclinic solution.
Moreover, given a nontrivial solution  of problem (3.1), there exist
of problem (3.1), there exist  two integer numbers such that for all
two integer numbers such that for all  and
and  , the sequence
, the sequence  is strictly monotone.
is strictly monotone.
(B) Higher Even-Order Difference Equations.
The statement of Theorem 1.1 can be extended to higher even-order difference equations. For simplicity we consider the fourth-order difference equations of the form

where  for each
for each  , satisfy the assumptions
, satisfy the assumptions  −
− .
.
We consider the functional  ,
,

where

which is well defined for  ,
, .
.
Note that the series  is convergent because
is convergent because

while  is convergent since
is convergent since  .
.
Now following the steps of the proof of Theorem 1.1 one can prove the following.
Theorem 3.2.
Suppose that  , the function
, the function  is positive and
is positive and  -periodic and the functions
-periodic and the functions  satisfy assumptions
satisfy assumptions  −
− and
and  ,
, . Then, for each
. Then, for each  , (3.8) has a nonzero homoclinic solution
, (3.8) has a nonzero homoclinic solution  , which is a critical point of the functional
, which is a critical point of the functional  .
.
A typical example of (3.8) is (3.2), which is a discretization of a fourth-order extended Fisher-Kolmogorov equation. Homoclinic solutions for fourth-order ODEs are studied in [7] using variational approach and concentration-compactness arguments. As a consequence of Theorem 3.2 we obtain the following corollary.
Corollary 3.3.
Suppose that  , the function
, the function  is positive and
is positive and  -periodic and
-periodic and  . Then, for each
. Then, for each  , (3.2) has a nonzero homoclinic solution
, (3.2) has a nonzero homoclinic solution  .
.
(C) Second-Order Difference Equations with Cubic and Quintic Nonlinearities.
Our next example is (3.3), known as stationary Ginzubrg-Landau equation with cubic-quintic nonlinearity. We refer to [18, 19] and references therein. From physical point of view it is interesting the case  ,
, ,
, . Theorem 1.1 can be applied for
. Theorem 1.1 can be applied for  with
with  ,
,  -periodic, and
-periodic, and  positive. Then
positive. Then  satisfies assumptions
satisfies assumptions  −
− with
with  and as a consequence we have the following corollary.
and as a consequence we have the following corollary.
Corollary 3.4.
Suppose that the functions  ,
,  and
and  are
are  -periodic and
-periodic and  and
and  are positive. Then, for each
are positive. Then, for each  , (3.3) has a nonzero homoclinic solution
, (3.3) has a nonzero homoclinic solution  .
.
Moreover, given a nontrivial solution  of problem (1.10), there exist
of problem (1.10), there exist  two integer numbers such that for all
two integer numbers such that for all  and
and  , the sequence
, the sequence  is strictly monotone.
is strictly monotone.
Moreover, we can prove that if in addition to conditions  −
− the following condition holds:
the following condition holds:
(F4)  ,
,
the homoclinic solution of (1.10) is positive.
Indeed, let  be a homoclinic solution of (1.10) and assume that
be a homoclinic solution of (1.10) and assume that  holds. Suppose that there exists
holds. Suppose that there exists  such that
such that  and let
and let  be such that
be such that  . In consequence
. In consequence  , which implies that
, which implies that

in contradiction with  . Then
. Then  for every
for every  .
.
If  for some
for some  , we know that
, we know that  and, in consequence,
and, in consequence,  , and we arrive at a contradiction as in the previous case.
, and we arrive at a contradiction as in the previous case.
We summarize above observations in the following.
Theorem 3.5.
Suppose that the function  is positive and
is positive and  -periodic and the functions
-periodic and the functions  satisfy assumptions
satisfy assumptions  ,
,  , and
, and  . Then, for each
. Then, for each  , (1.10) has a nonzero homoclinic solution
, (1.10) has a nonzero homoclinic solution  . If moreover
. If moreover  holds,
holds,  is a positive solution on
is a positive solution on  that is strictly monotone for
that is strictly monotone for  large enough.
large enough.
In the case  we can estimate the maximum of the solution
we can estimate the maximum of the solution  , provided the additional assumption
, provided the additional assumption
(F5) Assume that for all  and
and  function
function  has the form
has the form  , where
, where  is
is  -periodic in
-periodic in  ,
,  and for each
and for each  ,
,  is increasing in
is increasing in  for
for  .
.
Let  be the inverse function of
be the inverse function of  for
for  . We have that
. We have that  is increasing in
is increasing in  for
for  . Let
. Let  be a positive homoclinic solution of (1.10) in view of last theorem and
be a positive homoclinic solution of (1.10) in view of last theorem and  is its maximum. Note that, in view of the periodicity of coefficients, if
is its maximum. Note that, in view of the periodicity of coefficients, if  is a solution of (1.10), then
is a solution of (1.10), then  is also a solution of (1.10). Hence, we may assume that
is also a solution of (1.10). Hence, we may assume that  . Then
. Then  and
and

and hence by properties of  and
and 

Thus

We summarize above observation in the following.
Corollary 3.6.
Let  and suppose that the functions
and suppose that the functions  and
and  satisfy assumptions of Theorem 3.5. Then, if in addition,
satisfy assumptions of Theorem 3.5. Then, if in addition,  satisfies condition
satisfies condition  , the positive homoclinic solution of the equation
, the positive homoclinic solution of the equation

satisfies the estimate (3.15).
Our next example, concerning Theorem 3.5, are (3.4) and

where  .
.
Positive homoclinic solutions of corresponding differential equation are studied in [3] and periodic solutions in [20]. We suppose that the coefficients  ,
,  , and
, and  are
are  -periodic and there are constants
-periodic and there are constants  ,
, ,
, ,
, , and
, and  such that
such that

By Theorem 3.5, (3.17) has a positive solution  , which is a critical point of the functional
, which is a critical point of the functional  ,
,

Clearly, the positive solution of (3.17) is a positive solution of (3.4) too.
Further, let  take its positive maximum at
take its positive maximum at  , then
, then  and, since
and, since  , we have from (3.4) that
, we have from (3.4) that

In view of (3.18), the last inequality implies

or

We obtain a positive lower bound for  in the case
in the case

and (3.22) shows that  blows up, that is, tends to
blows up, that is, tends to  as
as  .
.
We summarize above facts in the following.
Corollary 3.7.
Let  and
and  and
and  be
be  -periodic sequences.
-periodic sequences.
Assume that there are constants  ,
, ,
, ,
, , and
, and  such that (3.18) holds. Then,
such that (3.18) holds. Then,

has a positive homoclinic solution and for  ,
,

Let  . By the last statement, if
. By the last statement, if  is the solution of the equation
is the solution of the equation

then

Let  be such that
be such that  . Since
. Since  is an infinite sequence of integers, by Dirichlet principle, there exists a fixed
is an infinite sequence of integers, by Dirichlet principle, there exists a fixed  and a subsequence of
and a subsequence of  , still denoted by
, still denoted by  , such that
, such that  and
and  . Note that if
. Note that if  , then
, then  or
or  .
.
Dedication
This work is dedicated to Professor Gheorghe Moroşanu on the occasion of his 60-th birthday.
References
Poincaré H: Les Méthodes Nouvelles de la Mécanique Céleste. Gauthier-Villars, Paris, France; 1899.
Coti Zelati V, Rabinowitz PH: Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. Journal of the American Mathematical Society 1991,4(4):693-727. 10.1090/S0894-0347-1991-1119200-3
Grossinho M, Minhós F, Tersian S: Positive homoclinic solutions for a class of second order differential equations. Journal of Mathematical Analysis and Applications 1999,240(1):163-173. 10.1006/jmaa.1999.6606
Omana W, Willem M: Homoclinic orbits for a class of Hamiltonian systems. Differential and Integral Equations 1992,5(5):1115-1120.
Rabinowitz PH: Homoclinic orbits for a class of Hamiltonian systems. Proceedings of the Royal Society of Edinburgh. Section A 1990,114(1-2):33-38. 10.1017/S0308210500024240
Tanaka K: Homoclinic orbits in a first order superquadratic Hamiltonian system: convergence of subharmonic orbits. Journal of Differential Equations 1991,94(2):315-339. 10.1016/0022-0396(91)90095-Q
Tersian S, Chaparova J: Periodic and homoclinic solutions of extended Fisher-Kolmogorov equations. Journal of Mathematical Analysis and Applications 2001,260(2):490-506. 10.1006/jmaa.2001.7470
Li C: A unified proof on existence of homoclinic orbits for some semilinear ordinary differential equations with periodic potentials. Journal of Mathematical Analysis and Applications 2010,365(2):510-516. 10.1016/j.jmaa.2009.11.013
Brezis H, Nirenberg L: Remarks on finding critical points. Communications on Pure and Applied Mathematics 1991,44(8-9):939-963. 10.1002/cpa.3160440808
Agarwal RP, Perera K, O'Regan D: Multiple positive solutions of singular and nonsingular discrete problems via variational methods. Nonlinear Analysis: Theory, Methods & Applications 2004,58(1-2):69-73. 10.1016/j.na.2003.11.012
Cabada A, Iannizzotto A, Tersian S: Multiple solutions for discrete boundary value problems. Journal of Mathematical Analysis and Applications 2009,356(2):418-428. 10.1016/j.jmaa.2009.02.038
Chen P, Fang H:Existence of periodic and subharmonic solutions for second-order
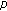 -Laplacian difference equations. Advances in Difference Equations 2007, 2007:-9.
-Laplacian difference equations. Advances in Difference Equations 2007, 2007:-9.Fang H, Zhao D: Existence of nontrivial homoclinic orbits for fourth-order difference equations. Applied Mathematics and Computation 2009,214(1):163-170. 10.1016/j.amc.2009.03.061
Jiang L, Zhou Z:Three solutions to Dirichlet boundary value problems for
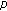 -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.Ma M, Guo Z: Homoclinic orbits for second order self-adjoint difference equations. Journal of Mathematical Analysis and Applications 2006,323(1):513-521. 10.1016/j.jmaa.2005.10.049
Mihăilescu M, Rădulescu V, Tersian S: Eigenvalue problems for anisotropic discrete boundary value problems. Journal of Difference Equations and Applications 2009,15(6):557-567. 10.1080/10236190802214977
Kristály A, Mihăilescu M, Rădulescu V, Tersian S: Spectral estimates for a nonhomogeneous difference problem. Communications in Contemporary Mathematics. In press
Efremidis NK, Christodoulides DN: Discrete Ginzburg-Landau solitons. Physical Review E 2003., 67:
Maruno K, Ankiewicz A, Akhmediev N: Dissipative solitons of the discrete complex cubic-quintic Ginzburg-Landau equation. Physics Letters A 2005,347(4–6):231-240. 10.1016/j.physleta.2005.08.028
Grossinho MR, Sanchez L: A note on periodic solutions of some nonautonomous differential equations. Bulletin of the Australian Mathematical Society 1986,34(2):253-265. 10.1017/S000497270001011X
Acknowledgment
S. Tersian is thankful to Department of Mathematical Analysis at University of Santiago de Compostela, Spain, where a part of this work was prepared during his visit. A. Cabada partially supported by Ministerio de Educación y Ciencia, Spain, project MTM2007-61724.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cabada, A., Li, C. & Tersian, S. On Homoclinic Solutions of a Semilinear 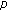 -Laplacian Difference Equation with Periodic Coefficients.
Adv Differ Equ 2010, 195376 (2010). https://doi.org/10.1155/2010/195376
-Laplacian Difference Equation with Periodic Coefficients.
Adv Differ Equ 2010, 195376 (2010). https://doi.org/10.1155/2010/195376
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/195376
 if
if  ,
,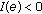 .
.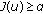 if
if  ,
,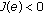 .
.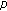 -Laplacian equations of the form
-Laplacian equations of the form 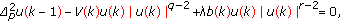
 -Laplacian difference equations. Advances in Difference Equations 2007, 2007:-9.
-Laplacian difference equations. Advances in Difference Equations 2007, 2007:-9. -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.