- Research Article
- Open access
- Published:
Some Identities of Bernoulli Numbers and Polynomials Associated with Bernstein Polynomials
Advances in Difference Equations volume 2010, Article number: 305018 (2010)
Abstract
We investigate some interesting properties of the Bernstein polynomials related to the bosonic  -adic integrals on
-adic integrals on  .
.
1. Introduction
Let  be the set of continuous functions on
be the set of continuous functions on  . Then the classical Bernstein polynomials of degree
. Then the classical Bernstein polynomials of degree  for
for  are defined by
are defined by

where  is called the Bernstein operator and
is called the Bernstein operator and

are called the Bernstein basis polynomials (or the Bernstein polynomials of degree  ). Recently, Acikgoz and Araci have studied the generating function for Bernstein polynomials (see [1, 2]). Their generating function for
). Recently, Acikgoz and Araci have studied the generating function for Bernstein polynomials (see [1, 2]). Their generating function for  is given by
is given by

where  and
and  . Note that
. Note that

for  (see [1, 2]). In [3], Simsek and Acikgoz defined generating function of the (
(see [1, 2]). In [3], Simsek and Acikgoz defined generating function of the ( -)Bernstein-Type Polynomials,
-)Bernstein-Type Polynomials,  as follows:
as follows:

where  . Observe that
. Observe that

Hence by the above one can very easily see that

Thus, we have arrived at the generating function in [1, 2] and also in (1.3) as well.
The Bernstein polynomials can also be defined in many different ways. Thus, recently, many applications of these polynomials have been looked for by many authors. Some researchers have studied the Bernstein polynomials in the area of approximation theory (see [1–7]). In recent years, Acikgoz and Araci [1, 2] have introduced several type Bernstein polynomials.
In the present paper, we introduce the Bernstein polynomials on the ring of  -adic integers
-adic integers  . We also investigate some interesting properties of the Bernstein polynomials related to the bosonic
. We also investigate some interesting properties of the Bernstein polynomials related to the bosonic  -adic integrals on the ring of
-adic integrals on the ring of  -adic integers
-adic integers  .
.
2. Bernstein Polynomials Related to the Bosonic  -Adic Integrals on
-Adic Integrals on 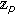
Let  be a fixed prime number. Throughout this paper,
be a fixed prime number. Throughout this paper,  ,
,  , and
, and  will denote the ring of
will denote the ring of  -adic integers, the field of
-adic integers, the field of  -adic numbers, and the completion of the algebraic closure of
-adic numbers, and the completion of the algebraic closure of  , respectively. Let
, respectively. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  . For
. For  , the bosonic distribution
, the bosonic distribution  on
on 

is known as the  -adic Haar distribution
-adic Haar distribution  where
where  (cf. [8]). We will write
(cf. [8]). We will write  to remind ourselves that
to remind ourselves that  is the variable of integration. Let
is the variable of integration. Let  be the space of uniformly differentiable function on
be the space of uniformly differentiable function on  . Then
. Then  yields the fermionic
yields the fermionic  -adic
-adic  -integral of a function
-integral of a function 

(cf. [8]). Many interesting properties of (2.2) were studied by many authors (cf. [8, 9] and the references given there). For  , write
, write  . We have
. We have

This identity is to derives interesting relationships involving Bernoulli numbers and polynomials. Indeed, we note that

where  are the Bernoulli polynomials (cf. [8]). From (1.2), we have
are the Bernoulli polynomials (cf. [8]). From (1.2), we have

By (2.5), we obtain the following proposition.
Proposition 2.1.
For  ,
,

From (2.4), we note that

with the usual convention of replacing  by
by  and
and  by
by  . Thus, we have
. Thus, we have

for  , since
, since  . Therefore we obtain the following theorem.
. Therefore we obtain the following theorem.
Theorem 2.2.
For  ,
,

Also we obtain

Therefore we obtain the following result.
Corollary 2.3.
For  ,
,

From the property of the Bernstein polynomials of degree  , we easily see that
, we easily see that

Continuing this process, we obtain the following theorem.
Theorem 2.4.
The multiplication of the sequence of Bernstein polynomials

for  with different degree under
with different degree under  -adic integral on
-adic integral on  , can be given as
, can be given as

We put

Theorem 2.5.
The multiplication of

Bernstein polynomials with different degrees  under
under  -adic integral on
-adic integral on  can be given as
can be given as

Theorem 2.6.
The multiplication of

Bernstein polynomials with different degrees  with different powers
with different powers  under
under  -adic integral on
-adic integral on  can be given as
can be given as

Problem 2.
Find the Witt's formula for the Bernstein polynomials in  -adic number field.
-adic number field.
References
Acikgoz M, Araci S: A study on the integral of the product of several type Bernstein polynomials. IST Transaction of Applied Mathematics-Modelling and Simulation. In press
Acikgoz M, Araci S: On the generating function of the Bernstein polynomials. In Proceedings of the 8th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM '10), March 2010, Rhodes, Greece. AIP;
Simsek Y, Acikgoz M:A new generating function of (
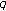 -) Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.
-) Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.Bernstein S: Demonstration du theoreme de Weierstrass, fondee sur le calcul des probabilities. Communications of the Kharkov Mathematical Society 1913, 13: 1-2.
Jang L-C, Kim W-J, Simsek Y:A study on the p-adic integral representation on
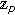 associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.
associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.Kim T, Jang L-C, Yi H:A note on the modified
 -bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.
-bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.Phillips GM:Bernstein polynomials based on the
 -integers. Annals of Numerical Mathematics 1997,4(1–4):511-518.
-integers. Annals of Numerical Mathematics 1997,4(1–4):511-518.Kim T:On a
 -analogue of the
-analogue of the 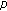 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373Kim T, Choi J, Kim Y-H:Some identities on the
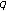 -Bernstein polynomials,
-Bernstein polynomials, 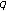 -Stirling numbers and
-Stirling numbers and  -Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010,20(3):335-341.
-Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010,20(3):335-341.
Acknowledgments
The first author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (2010-0001654). The second author was supported by the research grant of Kwangwoon University in 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, MS., Kim, T., Lee, B. et al. Some Identities of Bernoulli Numbers and Polynomials Associated with Bernstein Polynomials. Adv Differ Equ 2010, 305018 (2010). https://doi.org/10.1155/2010/305018
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/305018
 -Adic Integrals on
-Adic Integrals on 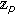
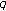 -) Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.
-) Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.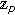 associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.
associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6. -bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.
-bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12. -integers. Annals of Numerical Mathematics 1997,4(1–4):511-518.
-integers. Annals of Numerical Mathematics 1997,4(1–4):511-518. -analogue of the
-analogue of the 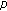 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373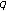 -Bernstein polynomials,
-Bernstein polynomials, 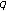 -Stirling numbers and
-Stirling numbers and  -Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010,20(3):335-341.
-Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010,20(3):335-341.