- Research Article
- Open access
- Published:
Existence of Periodic Solutions for 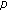 -Laplacian Equations on Time Scales
-Laplacian Equations on Time Scales
Advances in Difference Equations volume 2010, Article number: 584375 (2009)
Abstract
We systematically explore the periodicity of Liénard type  -Laplacian equations on time scales. Sufficient criteria are established for the existence of periodic solutions for such equations, which generalize many known results for differential equations when the time scale is chosen as the set of the real numbers. The main method is based on the Mawhin's continuation theorem.
-Laplacian equations on time scales. Sufficient criteria are established for the existence of periodic solutions for such equations, which generalize many known results for differential equations when the time scale is chosen as the set of the real numbers. The main method is based on the Mawhin's continuation theorem.
1. Introduction
In the past decades, periodic problems involving the scalar p-Laplacian were studied by many authors, especially for the second-order and three-order p-Laplacian differential equation, see [1–8] and the references therein. Of the aforementioned works, Lu in [1] investigated the existence of periodic solutions for a p-Laplacian Liénard differential equation with a deviating argument

by Mawhin's continuation theorem of coincidence degree theory [3]. The author obtained a new result for the existence of periodic solutions and investigated the relation between the existence of periodic solutions and the deviating argument  Cheung and Ren [4] studied the existence of
Cheung and Ren [4] studied the existence of  -periodic solutions for a p-Laplacian Liénard equation with a deviating argument
-periodic solutions for a p-Laplacian Liénard equation with a deviating argument

by Mawhin's continuation theorem. Two results for the existence of periodic solutions were obtained. Such equations are derived from many fields, such as fluid mechanics and elastic mechanics.
The theory of time scales has recently received a lot of attention since it has a tremendous potential for applications. For example, it can be used to describe the behavior of populations with hibernation periods. The theory of time scales was initiated by Hilger [9] in his Ph.D. thesis in 1990 in order to unify continuous and discrete analysis. By choosing the time scale to be the set of real numbers, the result on dynamic equations yields a result concerning a corresponding ordinary differential equation, while choosing the time scale as the set of integers, the same result leads to a result for a corresponding difference equation. Later, Bohner and Peterson systematically explore the theory of time scales and obtain many perfect results in [10] and [11]. Many examples are considered by the authors in these books.
But the research of periodic solutions on time scales has not got much attention, see [12–16]. The methods usually used to explore the existence of periodic solutions on time scales are many fixed point theory, upper and lower solutions, Masseras theorem, and so on. For example, Kaufmann and Raffoul in [12] use a fixed point theorem due to Krasnosel'ski to show that the nonlinear neutral dynamic system with delay

has a periodic solution. Using the contraction mapping principle the authors show that the periodic solution is unique under a slightly more stringent inequality.
The Mawhin's continuation theorem has been extensively applied to explore the existence problem in ordinary differential (difference) equations but rarely applied to dynamic equations on general time scales. In [13], Bohner et al. introduce the Mawhin's continuation theorem to explore the existence of periodic solutions in predator-prey and competition dynamic systems, where the authors established some suitable sufficient criteria by defining some operators on time scales.
In [14], Li and Zhang have studied the periodic solutions for a periodic mutualism model

on a time scale  by employing Mawhin's continuation theorem, and have obtained three sufficient criteria.
by employing Mawhin's continuation theorem, and have obtained three sufficient criteria.
Combining Brouwer's fixed point theorem with Horn's fixed point theorem, two classes of one-order linear dynamic equations on time scales

are considered in [15] by Liu and Li. The authors presented some interesting properties of the exponential function on time scales and obtain a sufficient and necessary condition that guarantees the existence of the periodic solutions of the equation 
In [16], Bohner et al. consider the system

easily verifiable sufficient criteria are established for the existence of periodic solutions of this class of nonautonomous scalar dynamic equations on time scales, the approach that authors used in this paper is based on Mawhin's continuation theorem.
In this paper, we consider the existence of periodic solutions for p-Laplacian equations on a time scales 

where  is a constant,
is a constant, 
 and
and  is a function with periodic
is a function with periodic  is a periodic time scale which has the subspace topology inherited from the standard topology on
is a periodic time scale which has the subspace topology inherited from the standard topology on  Sufficient criteria are established for the existence of periodic solutions for such equations, which generalize many known results for differential equations when the time scales are chosen as the set of the real numbers. The main method is based on the Mawhin's continuation theorem.
Sufficient criteria are established for the existence of periodic solutions for such equations, which generalize many known results for differential equations when the time scales are chosen as the set of the real numbers. The main method is based on the Mawhin's continuation theorem.
If  (1.7) reduces to the differential equation
(1.7) reduces to the differential equation

We will use Mawhin's continuation theorem to study (1.7).
2. Preliminaries
In this section, we briefly give some basic definitions and lemmas on time scales which are used in what follows. Let  be a time scale (a nonempty closed subset of
be a time scale (a nonempty closed subset of  ). The forward and backward jump operators
). The forward and backward jump operators  and the graininess
and the graininess  are defined, respectively, by
are defined, respectively, by

We say that a point  is left-dense if
is left-dense if  and
and  If
If  and
and  then
then  is called right-dense. A point
is called right-dense. A point  is called left-scattered if
is called left-scattered if  while right-scattered if
while right-scattered if  If
If  has a left-scattered maximum
has a left-scattered maximum  then we set
then we set  otherwise set
otherwise set  If
If  has a right-scattered minimum
has a right-scattered minimum  then set
then set  otherwise set
otherwise set 
A function  is right-dense continuous (rd-continuous) provided that it is continuous at right-dense point in
is right-dense continuous (rd-continuous) provided that it is continuous at right-dense point in  and its left side limits exist at left-dense points in
and its left side limits exist at left-dense points in  If
If  is continuous at each right-dense point and each left-dense point, then
is continuous at each right-dense point and each left-dense point, then  is said to be continuous function on
is said to be continuous function on 
Definition 2.1 (see [10]).
Assume  is a function and let
is a function and let  We define
We define  to be the number (if it exists) with the property that for a given
to be the number (if it exists) with the property that for a given  there exists a neighborhood
there exists a neighborhood  of
of  such that
such that

We call  the delta derivative of
the delta derivative of  at
at 
If  is continuous, then
is continuous, then  is right-dense continuous, and if
is right-dense continuous, and if  is delta differentiable at
is delta differentiable at  then
then  is continuous at
is continuous at 
Let  be right-dense continuous. If
be right-dense continuous. If  for all
for all  then we define the delta integral by
then we define the delta integral by

Definition 2.2 (see [12]).
We say that a time scale  is periodic if there is
is periodic if there is  such that if
such that if  then
then  For
For  the smallest positive
the smallest positive  is called the period of the time scale.
is called the period of the time scale.
Definition 2.3 (see [12]).
Let  be a periodic time scale with period
be a periodic time scale with period  We say that the function
We say that the function  is periodic with period
is periodic with period  if there exists a natural number
if there exists a natural number  such that
such that  for all
for all  and
and  is the smallest number such that
is the smallest number such that  If
If  we say that
we say that  is periodic with period
is periodic with period  if
if  is the smallest positive number such that
is the smallest positive number such that  for all
for all 
Lemma 2.4 (see [10]).
If  , and
, and  then
then
-
(A1)

-
(A2)
if
 for all
for all  then
then 
-
(A3)
if
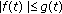 on
on  then
then 
Lemma 2.5 (H lder's inequality [11]).
lder's inequality [11]).
Let  For rd-continuous functions
For rd-continuous functions  one has
one has

where  and
and 
For convenience, we denote

where  is an
is an  -periodic real function, that is,
-periodic real function, that is,  for all
for all 
Next, let us recall the continuation theorem in coincidence degree theory. To do so, we introduce the following notations.
Let  be real Banach spaces,
be real Banach spaces,  a linear mapping,
a linear mapping,  a continuous mapping. The mapping
a continuous mapping. The mapping  will be called a Fredholm mapping of index zero if
will be called a Fredholm mapping of index zero if  and
and  is closed in
is closed in  If
If  is a Fredholm mapping of index zero and there exist continuous projections
is a Fredholm mapping of index zero and there exist continuous projections  such that
such that  then it follows that
then it follows that  is invertible. We denote the inverse of that map by
is invertible. We denote the inverse of that map by  If
If  is an open bounded subset of
is an open bounded subset of  the mapping
the mapping  will be called
will be called  -compact on
-compact on  if
if  is bounded and
is bounded and  is compact. Since
is compact. Since  is isomorphic to
is isomorphic to  there exists an isomorphism
there exists an isomorphism 
Lemma 2.6 (continuation theorem).
Suppose that  and
and  are two Banach spaces, and
are two Banach spaces, and  is a Fredholm operator of index 0. Furthermore, let
is a Fredholm operator of index 0. Furthermore, let  be an open bounded set and
be an open bounded set and  L-compact on
L-compact on  If
If
-
(B1)
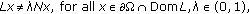
-
(B2)

-
(B3)
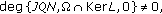 where
where  is an isomorphism,
is an isomorphism,
then the equation  has at least one solution in
has at least one solution in 
Lemma 2.7 (see [13]).
Let  and
and  If
If  is
is  -periodic, then
-periodic, then

In order to use Mawhin's continuation theorem to study the existence of  -periodic solutions for (1.7), we consider the following system:
-periodic solutions for (1.7), we consider the following system:

where  is a constant with
is a constant with  Clearly, if
Clearly, if  is an
is an  -periodic solution to (2.7), then
-periodic solution to (2.7), then  must be an
must be an  -periodic solution to (1.7). Thus, in order to prove that (1.7) has an
-periodic solution to (1.7). Thus, in order to prove that (1.7) has an  -periodic solution, it suffices to show that (2.7) has an
-periodic solution, it suffices to show that (2.7) has an  -periodic solution.
-periodic solution.
Now, we set  with the norm
with the norm  It is easy to show that
It is easy to show that  is a Banach space when it is endowed with the above norm
is a Banach space when it is endowed with the above norm 
Let

Then it is easy to show that  and
and  are both closed linear subspaces of
are both closed linear subspaces of  We claim that
We claim that  and
and  Since for any
Since for any  we have
we have  and
and

so we obtain 
Take  Define
Define

by

and  by
by

Define the operator  and
and  by
by

It is easy to see that (2.7) can be converted to the abstract equation 
Then  and
and  Since
Since  is closed in
is closed in  it follows that
it follows that  is a Fredholm mapping of index zero. It is not difficult to show that
is a Fredholm mapping of index zero. It is not difficult to show that  and
and  are continuous projections such that
are continuous projections such that  and
and  Furthermore, the generalized inverse (to
Furthermore, the generalized inverse (to  )
)  exists and is given by
exists and is given by

Since for every  we have
we have

from the definition of  and the condition that
and the condition that  then
then  Thus, we get
Thus, we get  Similarly, we can prove that
Similarly, we can prove that  for every
for every  So the operator
So the operator  is well defined. Thus,
is well defined. Thus,

Denote  We have
We have

Clearly,  and
and  are continuous. Since
are continuous. Since  is a Banach space, it is easy to show that
is a Banach space, it is easy to show that  is a compact for any open bounded set
is a compact for any open bounded set  Moreover,
Moreover,  is bounded. Thus,
is bounded. Thus,  is
is  -compact on
-compact on 
3. Main Results
In this section, we present our main results.
Theorem 3.1.
Suppose that there exist positive constants  and
and  such that the following conditions hold:
such that the following conditions hold:
-
(i)
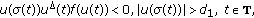
-
(ii)
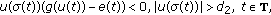
then (1.7) has at least one  -periodic solution.
-periodic solution.
Proof.
Consider the equation  where
where  and
and  are defined by the second section. Let
are defined by the second section. Let 
If  then we have
then we have

From the first equation of (3.1), we obtain  and then by substituting it into the second equation of (3.1), we get
and then by substituting it into the second equation of (3.1), we get

Integrating both sides of (3.2) from  to
to  noting that
noting that  and applying Lemma 2.4, we have
and applying Lemma 2.4, we have

that is,

There must exist  such that
such that

From conditions (i) and (ii), when  we have
we have  and
and  which contradicts to (3.5). Consequently
which contradicts to (3.5). Consequently  Similarly, there must exist
Similarly, there must exist  such that
such that

Then we have  Applying Lemma 2.7, we get
Applying Lemma 2.7, we get

Let  Then (3.7) equals to the following inequality:
Then (3.7) equals to the following inequality:

Let 
Consider the second equation of (3.1) and (3.8), then we have

Applying Lemma 2.5, we obtain that

where

That is,

Thus,

Since  then we obtain that there exists a positive constant
then we obtain that there exists a positive constant  such that
such that

Therefore,

Let  If
If  then
then  is a constant vector with
is a constant vector with

From the second equation of (3.16) we get

that is,

By assumptions (i) and (ii), we see that  and
and  which implies
which implies 
Now, we set  Then
Then  Thus from (3.8) and (3.14), we see that conditions (B1) and (B2) of Lemma 2.6 are satisfied. The remainder is verifying condition (B3) of Lemma 2.6. In order to do it, let
Thus from (3.8) and (3.14), we see that conditions (B1) and (B2) of Lemma 2.6 are satisfied. The remainder is verifying condition (B3) of Lemma 2.6. In order to do it, let

Set

It is easy to see that the equation  that is,
that is,

has no solution in  So
So 
Let

If  then we get
then we get

so we have

Then we see that

so the condition (B3) of Lemma 2.6 is satisfied, the proof is complete.
When  where
where  we have the following result.
we have the following result.
Corollary 3.2.
Suppose that the following conditions hold:
-
(i)

-
(ii)
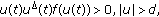
then (1.7) has at least one  -periodic solution.
-periodic solution.
References
Lu S:Existence of periodic solutions to a
 -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041Xiao B, Liu B:Periodic solutions for Rayleigh type
 -Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010
-Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010Gaines RE, Mawhin JL: Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics. Volume 568. Springer, Berlin, Germany; 1977:i+262.
Cheung WS, Ren JL:On the existence of periodic solutions for
 -Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.
-Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.Zhang FX, Li Y:Existence and uniqueness of periodic solutions for a kind of Duffing type
 -Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013
-Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013Liu B:Existence and uniqueness of periodic solutions for a kind of Liénard type
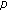 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007Manásevich R, Mawhin J:Periodic solutions for nonlinear systems with
 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425Cao FJ, Han ZL:Existence of periodic solutions for
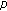 -Laplacian differential equation with deviating arguments. Journal of Uuniversity of Jinan (Science & Technology) 2010, 24: 1-4.
-Laplacian differential equation with deviating arguments. Journal of Uuniversity of Jinan (Science & Technology) 2010, 24: 1-4.Hilger S: Analysis on measure chains-a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Kaufmann ER, Raffoul YN: Periodic solutions for a neutral nonlinear dynamical equation on a time scale. Journal of Mathematical Analysis and Applications 2006,319(1):315-325. 10.1016/j.jmaa.2006.01.063
Bohner M, Fan M, Zhang JM: Existence of periodic solutions in predator-prey and competition dynamic systems. Nonlinear Analysis: Real World Applications 2006,7(5):1193-1204. 10.1016/j.nonrwa.2005.11.002
Li YK, Zhang HT: Existence of periodic solutions for a periodic mutualism model on time scales. Journal of Mathematical Analysis and Applications 2008,343(2):818-825. 10.1016/j.jmaa.2008.02.002
Liu XL, Li WT: Periodic solutions for dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2007,67(5):1457-1463. 10.1016/j.na.2006.07.030
Bohner M, Fan M, Zhang JM: Periodicity of scalar dynamic equations and applications to population models. Journal of Mathematical Analysis and Applications 2007,330(1):1-9. 10.1016/j.jmaa.2006.04.084
Acknowledgments
The authors sincerely thank the reviewers for their valuable suggestions and useful comments that have led to the present improved version of the original manuscript. This research is supported by the Natural Science Foundation of China (60774004, 60904024), China Postdoctoral Science Foundation Funded Project (20080441126, 200902564), Shandong Postdoctoral Funded Project (200802018) and supported by Shandong Research Funds (Y2008A28), also supported by University of Jinan Research Funds for Doctors (B0621, XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, F., Han, Z. & Sun, S. Existence of Periodic Solutions for 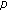 -Laplacian Equations on Time Scales.
Adv Differ Equ 2010, 584375 (2009). https://doi.org/10.1155/2010/584375
-Laplacian Equations on Time Scales.
Adv Differ Equ 2010, 584375 (2009). https://doi.org/10.1155/2010/584375
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/584375

 for all
for all  then
then 
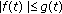 on
on  then
then 
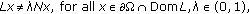

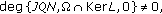 where
where  is an isomorphism,
is an isomorphism,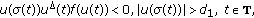
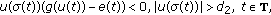

 -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041 -Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010
-Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010 -Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.
-Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75. -Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013
-Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425 -Laplacian differential equation with deviating arguments. Journal of Uuniversity of Jinan (Science & Technology) 2010, 24: 1-4.
-Laplacian differential equation with deviating arguments. Journal of Uuniversity of Jinan (Science & Technology) 2010, 24: 1-4.