- Research Article
- Open access
- Published:
Three Solutions for a Discrete Nonlinear Neumann Problem Involving the 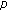 -Laplacian
-Laplacian
Advances in Difference Equations volume 2010, Article number: 862016 (2010)
Abstract
We investigate the existence of at least three solutions for a discrete nonlinear Neumann boundary value problem involving the  -Laplacian. Our approach is based on three critical points theorems.
-Laplacian. Our approach is based on three critical points theorems.
1. Introduction
In these last years, the study of discrete problems subject to various boundary value conditions has been widely approached by using different abstract methods as fixed point theorems, lower and upper solutions, and Brower degree (see, e.g., [1–3] and the reference given therein). Recently, also the critical point theory has aroused the attention of many authors in the study of these problems [4–12].
The main aim of this paper is to investigate different sets of assumptions which guarantee the existence and multiplicity of solutions for the following nonlinear Neumann boundary value problem

where  is a fixed positive integer,
is a fixed positive integer,  is the discrete interval
is the discrete interval  ,
,  for all
for all  ,
,  is a positive real parameter,
is a positive real parameter,  ,
,  , is the forward difference operator,
, is the forward difference operator,  ,
,  , and
, and  is a continuous function.
is a continuous function.
In particular, for every  lying in a suitable interval of parameters, at least three solutions are obtained under mutually independent conditions. First, we require that the primitive
lying in a suitable interval of parameters, at least three solutions are obtained under mutually independent conditions. First, we require that the primitive  of
of  is
is  sublinear at infinity and satisfies appropriate local growth condition (Theorem 3.1). Next, we obtain at least three positive solutions uniformly bounded with respect to
sublinear at infinity and satisfies appropriate local growth condition (Theorem 3.1). Next, we obtain at least three positive solutions uniformly bounded with respect to  , under a suitable sign hypothesis on
, under a suitable sign hypothesis on  , an appropriate growth conditions on
, an appropriate growth conditions on  in a bounded interval, and without assuming asymptotic condition at infinity on
in a bounded interval, and without assuming asymptotic condition at infinity on  (Theorem 3.4, Corollary 3.6). Moreover, the existence of at least two nontrivial solutions for problem () is obtained assuming that
(Theorem 3.4, Corollary 3.6). Moreover, the existence of at least two nontrivial solutions for problem () is obtained assuming that  is
is  sublinear at zero and
sublinear at zero and  superlinear at infinity (Theorem 3.5).
superlinear at infinity (Theorem 3.5).
It is worth noticing that it is the first time that this type of results are obtained for discrete problem with Neumann boundary conditions; instead of Dirichlet problem, similar results have been already given in [6, 9, 13]. Moreover, in [14], the existence of multiple solutions to problem () is obtained assuming different hypotheses with respect to our assumptions (see Remark 3.7).
Investigation on the relation between continuous and discrete problems are available in the papers [15, 16]. General references on difference equations and their applications in different fields of research are given in [17, 18]. While for an overview on variational methods, we refer the reader to the comprehensive monograph [19].
2. Critical Point Theorems and Variational Framework
Let  be a real Banach space, let
be a real Banach space, let  be two functions of class
be two functions of class  on
on  , and let
, and let  be a positive real parameter. In order to study problem (), our main tools are critical points theorems for functional of type
be a positive real parameter. In order to study problem (), our main tools are critical points theorems for functional of type  which insure the existence at least three critical points for every
which insure the existence at least three critical points for every  belonging to well-defined open intervals. These theorems have been obtained, respectively, in [6, 20, 21].
belonging to well-defined open intervals. These theorems have been obtained, respectively, in [6, 20, 21].
Theorem 2.1 (see [11, Theorem 2.6]).
Let  be a reflexive real Banach space,
be a reflexive real Banach space,  be a coercive, continuously Gâteaux differentiable and sequentially weakly lower semicontinuous functional whose Gâteaux derivative admits a continuous inverse on
be a coercive, continuously Gâteaux differentiable and sequentially weakly lower semicontinuous functional whose Gâteaux derivative admits a continuous inverse on  ,
,  be a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact such that
be a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact such that

Assume that there exist  and
and  , with
, with  such that
such that
()  ,
,
() for each  the functional
the functional  is coercive.
is coercive.
Then, for each  , the functional
, the functional  has at least three distinct critical points in
has at least three distinct critical points in  .
.
Theorem 2.2 (see [7, Corollary 3.1]).
Let  be a reflexive real Banach space,
be a reflexive real Banach space,  be a convex, coercive, and continuously Gâteaux differentiable functional whose Gâteaux derivative admits a continuous inverse on
be a convex, coercive, and continuously Gâteaux differentiable functional whose Gâteaux derivative admits a continuous inverse on  , and let
, and let  be a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact such that
be a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact such that

Assume that there exist two positive constants  ,
,  and
and  , with
, with  such that
such that
(b1) ,
,
(b2) ,
,
(b3) for each  ,
,  and for every
and for every  , which are local minima for the functional
, which are local minima for the functional  such that
such that  and
and  , and one has
, and one has  .
.
Then, for each  , the functional
, the functional  admits at least three critical points which lie in
admits at least three critical points which lie in  .
.
Finally, for all  , we put
, we put

where we read  if this case occurs.
if this case occurs.
Theorem 2.3 (see [8, Theorem 2.3]).
Let  be a finite dimensional real Banach space. Assume that for each
be a finite dimensional real Banach space. Assume that for each  one has
one has
(e) .
.
Then, for each  , the functional
, the functional  admits at least three distinct critical points.
admits at least three distinct critical points.
Remark 2.4.
It is worth noticing that whenever  is a finite dimensional Banach space, a careful reading of the proofs of Theorems 2.1 and 2.2 shows that regarding to the regularity of the derivative of
is a finite dimensional Banach space, a careful reading of the proofs of Theorems 2.1 and 2.2 shows that regarding to the regularity of the derivative of  and
and  , it is enough to require only that
, it is enough to require only that  and
and  are two continuous functionals on
are two continuous functionals on  .
.
Now, consider the  -dimensional normed space
-dimensional normed space  endowed with the norm
endowed with the norm

In the sequel, we will use the following inequality:

Moreover, put

where  for every
for every  . It is easy to show that
. It is easy to show that  and
and  are two
are two  functionals on
functionals on  .
.
Next lemma describes the variational structure of problem (), for the reader convenience we give a sketch of the proof, see also [14],
Lemma 2.5.
 is a Banach space. Let
is a Banach space. Let  ,
,  be a solution of problem () if and only if
be a solution of problem () if and only if  is a critical point of the functional
is a critical point of the functional  .
.
Proof.
Bearing in mind both that a finite dimensional normed space is a Banach space and the following partial sum:

for every  and
and  , standard variational arguments complete the proof.
, standard variational arguments complete the proof.
Finally, we point out the following strong maximum principle for problem ().
Lemma 2.6.
Fix  such that
such that

Then, either  in
in  , or
, or  .
.
Proof.
Let  be such that
be such that  . An immediate computation gives
. An immediate computation gives

From this, by (2.8), we obtain

so  , that is
, that is  . Moreover, assuming that
. Moreover, assuming that  , from the preciding inequality and nonnegativity of
, from the preciding inequality and nonnegativity of  , one has
, one has

so  . Thus, repeating these arguments, the conclusion follows at once.
. Thus, repeating these arguments, the conclusion follows at once.
3. Main Results
For each positive constants  and
and  , we write
, we write

Now, we give the main results.
Theorem 3.1.
Assume that there exist three positive constants  ,
,  , and
, and  with
with  , and
, and  such that
such that
(i1) ,
,
(i2) .
.
Then, for every

problem (Pλf) admits at least three solutions.
Proof.
We apply Theorem 2.1, by putting  and
and  defined as in (2.6) on the space
defined as in (2.6) on the space  . An easy computation ensures the regularity assumptions required on
. An easy computation ensures the regularity assumptions required on  and
and  ; see Remark 2.4. Therefore, it remains to verify assumptions (
; see Remark 2.4. Therefore, it remains to verify assumptions ( ) and (
) and ( ). To this hand, we put
). To this hand, we put

and we pick  , defined by putting
, defined by putting

Clearly, since  , one has
, one has  , and in addition, by (2.5), we have
, and in addition, by (2.5), we have

On the other hand, we compute

Therefore, by ( ), combining (3.5) and (3.6), it is clear that (
), combining (3.5) and (3.6), it is clear that ( ) holds. Moreover, one has
) holds. Moreover, one has

Now, fix  as in the conclusion; first, we observe that for every
as in the conclusion; first, we observe that for every  , one has
, one has

Next, by ( ), there exist two positive constants
), there exist two positive constants  and
and  such that
such that

Hence, for every  , we get
, we get

At this point, since  , it is clear that the functional
, it is clear that the functional  turns out to be coercive.
turns out to be coercive.
Remark 3.2.
We note that hypothesis ( ) can be replaced with the following:
) can be replaced with the following:
(i21)  .
.
Arguing as before, there exist two constant  and
and  such that
such that

Hence, for every  , it easy to see that
, it easy to see that

with  .
.
Remark 3.3.
It is worth noticing that a careful reading of the proof of Theorem 3.1 shows that, provided that  and under the only condition (
and under the only condition ( ), problem () admits at least one solution for every
), problem () admits at least one solution for every  and at least three solutions for every
and at least three solutions for every  , whenever there exists
, whenever there exists  for which
for which  .
.
Theorem 3.4.
Let  be a continuous function in
be a continuous function in  such that
such that  for some
for some  . Assume that there exist three positive constants
. Assume that there exist three positive constants  ,
,  , and
, and  with
with  such that
such that
() for each
for each  ,
,
() .
.
Then, for each  , problem () admits at least three positive solutions
, problem () admits at least three positive solutions  ,
,  , such that
, such that

for all  ,
,  .
.
Proof.
Consider the auxiliary problem

where  is a continuous function defined putting
is a continuous function defined putting

From ( ), owing to Lemma 2.6, any solution of problem () is positive. In addition, if it satisfies also the condition
), owing to Lemma 2.6, any solution of problem () is positive. In addition, if it satisfies also the condition  , and for every
, and for every  , clearly it turns to be also a positive solution of (). Therefore, for our goal, it is enough to show that our conclusion holds for (). In this connection, our aim is to apply Theorem 2.2. Fix
, clearly it turns to be also a positive solution of (). Therefore, for our goal, it is enough to show that our conclusion holds for (). In this connection, our aim is to apply Theorem 2.2. Fix  in
in  and let
and let  ,
,  and
and  as before. Now, take
as before. Now, take

From (2.5), arguing as before, we obtain

for all  such that
such that  , and
, and

for all  such that
such that  .
.
Therefore, one has

as well as

On the other hand, pick  , defined as in (3.4), bearing in mind (3.6), and from
, defined as in (3.4), bearing in mind (3.6), and from  , we obtain
, we obtain  Moreover, taking into account (3.18), (3.19), from (
Moreover, taking into account (3.18), (3.19), from ( ), assumptions (
), assumptions ( ) and (
) and ( ) follow. Further, again from (3.18), (3.19), and (3.6), one has that
) follow. Further, again from (3.18), (3.19), and (3.6), one has that

Now, let  and
and  be two local minima for
be two local minima for  such that
such that  and
and  . Owing to Lemmas 2.5 and 2.6, they are two positive solutions for () so
. Owing to Lemmas 2.5 and 2.6, they are two positive solutions for () so  , for all
, for all  and for all
and for all  . Hence, since one has
. Hence, since one has  for all
for all  ,
,  is verified.
is verified.
Therefore, the functional  admits at least three critical points
admits at least three critical points  ,
,  , which are three positive solutions of (). Finally, from (2.5), for
, which are three positive solutions of (). Finally, from (2.5), for  , one has
, one has

and the proof is completed.
Theorem 3.5.
Let  be a continuous function such that
be a continuous function such that  for some
for some  . Assume that there exist four constants
. Assume that there exist four constants  ,
,  ,
,  , and
, and  , with
, with  ,
,  and
and  such that
such that
() , for all
, for all  .
.
Then, for each  , where
, where

problem () admits at least three nontrivial solutions.
Proof.
Our aim is to apply Theorem 2.3 with  and
and  as above. Fix
as above. Fix  , and there is
, and there is  such that
such that  . Setting
. Setting  and arguing as in the proof of Theorem 3.1, one has
and arguing as in the proof of Theorem 3.1, one has

that is  . Moreover, denote
. Moreover, denote

it is a simple matter to show that for each  , one has
, one has

Hence, from ( ), for each
), for each  , we get
, we get

Therefore, since  and
and  , condition (
, condition ( ) is verified. Hence, from Theorem 2.3, the functional
) is verified. Hence, from Theorem 2.3, the functional  admits three critical points, which are three solutions for (). Since
admits three critical points, which are three solutions for (). Since  for some
for some  , they are nontrivial solutions, and the conclusion is proved.
, they are nontrivial solutions, and the conclusion is proved.
Corollary 3.6.
Let  be a continuous function such that
be a continuous function such that  for some
for some  . Assume that there exist four constants
. Assume that there exist four constants  ,
,  ,
,  , and
, and  with
with  and
and  such that
such that
(l1) ,
,
(l2) , for all
, for all  .
.
Then, for every

problem () admits at least three solutions.
Proof.
Our claim is to prove that condition ( ) of Theorem 2.3 holds for every
) of Theorem 2.3 holds for every  . Indeed, from (
. Indeed, from ( ), arguing as in (3.23), one has that
), arguing as in (3.23), one has that  . Moreover, by (
. Moreover, by ( ), from (3.26) with
), from (3.26) with  , for every
, for every  , we have
, we have

where  , which implies condition (
, which implies condition ( ).
).
Remark 3.7.
In [14], by Mountain Pass Theorem, the authors established the existence of at least one solution for problem () requiring the following conditions:
(θ1)  for
for  uniformly in
uniformly in  ,
,
(θ2) there exist two positive constants  and
and  with
with  such that
such that

for every  and
and  .
.
Moreover, they remember that the above conditions imply, respectively, the following:
(θ3)  for
for  uniformly in
uniformly in  ,
,
(θ4) there exist two positive constants  and
and  such that
such that

Next result shows that under more general conditions than ( ) and (
) and ( ), problem (
), problem ( ) has at least two nontrivial solutions.
) has at least two nontrivial solutions.
Theorem 3.8.
Assume that ( ) holds and in addition
) holds and in addition
(θ5) .
.
Then, problem ( ) has at least two nontrivial solutions.
) has at least two nontrivial solutions.
Proof.
We claim that the functional  admits a local minimum at zero and a local nonzero maximum. To this end, we observe that by (
admits a local minimum at zero and a local nonzero maximum. To this end, we observe that by ( ), there exist
), there exist  and
and  such that
such that

Hence, bearing in mind Lemma 2.5 and (3.25), with  , for every
, for every  with
with  , we get
, we get

that is, 0 is a local minimum. Moreover, by ( ), by now, it is evident that the functional
), by now, it is evident that the functional  is anticoercive in
is anticoercive in  . Hence, by the regularity of
. Hence, by the regularity of  , there exists
, there exists  which is a global maximum for the functional. Therefore, since it is not restrictive to suppose that
which is a global maximum for the functional. Therefore, since it is not restrictive to suppose that  (otherwise, there are infinitely many critical points), our conclusion follows: if
(otherwise, there are infinitely many critical points), our conclusion follows: if  , from Corollary 2.11 of [22] which ensures a third critical point different from 0 and
, from Corollary 2.11 of [22] which ensures a third critical point different from 0 and  and by standards arguments if
and by standards arguments if  .
.
References
Anderson DR, Rachůnková I, Tisdell CC: Solvability of discrete Neumann boundary value probles. Advances in Differential Equations 2007, 2: 93-99.
Bereanu C, Mawhin J:Boundary value problems for second-order nonlinear difference equations with discrete
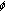 -Laplacian and singular
-Laplacian and singular  . Journal of Difference Equations and Applications 2008,14(10-11):1099-1118. 10.1080/10236190802332290
. Journal of Difference Equations and Applications 2008,14(10-11):1099-1118. 10.1080/10236190802332290Rachůnková I, Tisdell CC: Existence of non-spurious solutions to discrete Dirichlet problems with lower and upper solutions. Nonlinear Analysis: Theory, Methods & Applications 2007,67(4):1236-1245. 10.1016/j.na.2006.07.010
Agarwal RP, Perera K, O'Regan D: Multiple positive solutions of singular and nonsingular discrete problems via variational methods. Nonlinear Analysis: Theory, Methods & Applications 2004,58(1-2):69-73. 10.1016/j.na.2003.11.012
Agarwal RP, Perera K, O'Regan D:Multiple positive solutions of singular discrete
 -Laplacian problems via variational methods. Advances in Difference Equations 2005, (2):93-99. 10.1155/ADE.2005.93
-Laplacian problems via variational methods. Advances in Difference Equations 2005, (2):93-99. 10.1155/ADE.2005.93Bonanno G, Candito P: Nonlinear difference equations investigated via critical point methods. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3180-3186. 10.1016/j.na.2008.04.021
Bonanno G, Candito P: Infinitely many solutions for a class of discrete non-linear boundary value problems. Applicable Analysis 2009,88(4):605-616. 10.1080/00036810902942242
Bonanno G, Candito P: Difference equations through variational methods. In Handbook on Nonconvex Analysis. Edited by: Gao DY, Motreanu D. International Press of Boston, Sommerville, Boston, Mass, USA; 2010:1-44.
Candito P, D'Aguì G: Three solutions to a perturbed nonlinear discrete Dirichlet problem. Journal of Mathematical Analysis and Applications 2011,375(2):594-601. 10.1016/j.jmaa.2010.09.050
Candito P, Molica Bisci G: Existence of two solutions for a nonlinear second-order discrete boundary value problem. to appear in Advanced Nonlinear Studies
Jiang L, Zhou Z:Three solutions to Dirichlet boundary value problems for
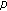 -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.Kristély A, Mihailescu M, Radulescu V: Discrete boundary value problems involving oscillatory nonlinearities: small and large solutions. Journal of Difference Equations and Applications. In press
Candito P, Giovannelli N:Multiple solutions for a discrete boundary value problem involving the
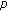 -Laplacian. Computers & Mathematics with Applications 2008,56(4):959-964. 10.1016/j.camwa.2008.01.025
-Laplacian. Computers & Mathematics with Applications 2008,56(4):959-964. 10.1016/j.camwa.2008.01.025Tian Y, Ge W:The existence of solutions for a second-order discrete Neumann problem with a
 -Laplacian. Journal of Applied Mathematics and Computing 2008,26(1-2):333-340. 10.1007/s12190-007-0012-5
-Laplacian. Journal of Applied Mathematics and Computing 2008,26(1-2):333-340. 10.1007/s12190-007-0012-5Agarwal RP: On multipoint boundary value problems for discrete equations. Journal of Mathematical Analysis and Applications 1983,96(2):520-534. 10.1016/0022-247X(83)90058-6
Lovász L: Discrete and continuous: two sides of the same? Geometric and Functional Analysis 2000, 359-382.
Agarwal RP: Difference Equations and Inequalities: Theory, Methods and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Kelley WG, Peterson AC: Difference Equations: An Introduction with Applications. Academic Press, Boston, Mass, USA; 1991:xii+455.
Struwe M: Variational Methods, Results in Mathematics and Related Areas (3). Volume 34. 2nd edition. Springer, Berlin, Germany; 1996:xvi+272.
Bonanno G, Marano SA: On the structure of the critical set of non-differentiable functions with a weak compactness condition. Applicable Analysis 2010,89(1):1-10. 10.1080/00036810903397438
Bonanno G, Candito P: Non-differentiable functionals and applications to elliptic problems with discontinuous nonlinearities. Journal of Differential Equations 2008,244(12):3031-3059. 10.1016/j.jde.2008.02.025
Fang G: On the existence and the classification of critical points for non-smooth functionals. Canadian Journal of Mathematics 1995,47(4):684-717. 10.4153/CJM-1995-036-9
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Candito, P., D'Aguì, G. Three Solutions for a Discrete Nonlinear Neumann Problem Involving the 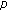 -Laplacian.
Adv Differ Equ 2010, 862016 (2010). https://doi.org/10.1155/2010/862016
-Laplacian.
Adv Differ Equ 2010, 862016 (2010). https://doi.org/10.1155/2010/862016
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/862016
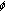 -Laplacian and singular
-Laplacian and singular  . Journal of Difference Equations and Applications 2008,14(10-11):1099-1118. 10.1080/10236190802332290
. Journal of Difference Equations and Applications 2008,14(10-11):1099-1118. 10.1080/10236190802332290 -Laplacian problems via variational methods. Advances in Difference Equations 2005, (2):93-99. 10.1155/ADE.2005.93
-Laplacian problems via variational methods. Advances in Difference Equations 2005, (2):93-99. 10.1155/ADE.2005.93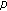 -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.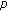 -Laplacian. Computers & Mathematics with Applications 2008,56(4):959-964. 10.1016/j.camwa.2008.01.025
-Laplacian. Computers & Mathematics with Applications 2008,56(4):959-964. 10.1016/j.camwa.2008.01.025 -Laplacian. Journal of Applied Mathematics and Computing 2008,26(1-2):333-340. 10.1007/s12190-007-0012-5
-Laplacian. Journal of Applied Mathematics and Computing 2008,26(1-2):333-340. 10.1007/s12190-007-0012-5