- Research Article
- Open access
- Published:
Limit Cycles of a Class of Hilbert's Sixteenth Problem Presented by Fractional Differential Equations
Advances in Difference Equations volume 2010, Article number: 938180 (2010)
Abstract
The second part of Hilbert's sixteenth problem concerned with the existence and number of the limit cycles for planer polynomial differential equations of degree n. In this article after a brief review on previous studies of a particular class of Hilbert's sixteenth problem, we will discuss the existence and the stability of limit cycles of this class in the form of fractional differential equations.
1. Introduction
The second part of the well-known Hilbert's 16th problem is still unsolved since Hilbert proposed it in 1900. This problem is concerned with the maximum number of limit cycles and their relative distributions of the real planar polynomial systems of degree n in the form of

where  and
and  are polynomial of degree
are polynomial of degree  with real coefficients. The general form of this problem, even for
with real coefficients. The general form of this problem, even for  , is yet an open problem that has attracted more researches but it is remarkably inflexible. With the development of computer's and graphical software, many recent new improvement results have been obtained. Some survey articles can be found in [1–5] and references therein. One of the classical methods to produce and study limit cycles in such system (1.1) is by perturbing a system which has a centre (e.g., see [6, 7]). In such methods the limit cycles are produced in the perturbed system from the periodic orbits of the periodic annulus of the unperturbed system. As we can see in [8] by perturbing the linear centre
, is yet an open problem that has attracted more researches but it is remarkably inflexible. With the development of computer's and graphical software, many recent new improvement results have been obtained. Some survey articles can be found in [1–5] and references therein. One of the classical methods to produce and study limit cycles in such system (1.1) is by perturbing a system which has a centre (e.g., see [6, 7]). In such methods the limit cycles are produced in the perturbed system from the periodic orbits of the periodic annulus of the unperturbed system. As we can see in [8] by perturbing the linear centre 
 , using arbitrary polynomials
, using arbitrary polynomials  and
and  of degree n,
of degree n,  limit cycles bifurcated with the bifurcation parameter
limit cycles bifurcated with the bifurcation parameter  of order one. Almost the same argument can be seen in [9] by perturbing the system
of order one. Almost the same argument can be seen in [9] by perturbing the system 
 with maximum n limit cycles. By perturbing the Hamiltonian centre given by
with maximum n limit cycles. By perturbing the Hamiltonian centre given by  in the polynomial differential systems of odd degree n, we can obtain
in the polynomial differential systems of odd degree n, we can obtain  limit cycles [10]. Several other similar investigations have been done using the perturbed polynomial differential systems of second, third, or even more degree. For example, see [11–13] and references therein.
limit cycles [10]. Several other similar investigations have been done using the perturbed polynomial differential systems of second, third, or even more degree. For example, see [11–13] and references therein.
Based on the above studies, some of the authors of this article investigated the number of limit cycles of perturbed quintic Hamiltonian systems with different degree polynomials [14, 15]. In these former articles a weakened Hilbert's 16th problem in the following form is considered:

In system (1.2)  is a real polynomial of degree n, and
is a real polynomial of degree n, and  and
and  are two real polynomial of degree m. Moreover, system (1.2) contains at least a family of closed orbits for any level curve
are two real polynomial of degree m. Moreover, system (1.2) contains at least a family of closed orbits for any level curve  with
with  and
and  . A full investigation of this planar system for the number of limit cycles and their stabilities can be found in [15]. In this article we study the existence of limit cycles and their stabilities for such system in the form of Fractional Differential Equations (FDEs). Recently great considerations have been made to the systems of FDE. The most essential property of these systems is their nonlocal property which does not exist in the integer-order differential operators. We mean by this property that the next state of a system depends not only upon its current state but also upon all of its historical states. This is a more realistic and is one reason why fractional calculus has become more and more popular. On the other hand, the integer-order differential operator is indifferent to its history. Furthermore, there have been several recent mathematical discoveries that have helped to unlock the power of the fractional derivative [16]. One such discovery is that of fractal functions. Indeed, most of the functions that we are familiar with are smooth. This means that locally they can be approximated by a straight line segment. For example, the function
. A full investigation of this planar system for the number of limit cycles and their stabilities can be found in [15]. In this article we study the existence of limit cycles and their stabilities for such system in the form of Fractional Differential Equations (FDEs). Recently great considerations have been made to the systems of FDE. The most essential property of these systems is their nonlocal property which does not exist in the integer-order differential operators. We mean by this property that the next state of a system depends not only upon its current state but also upon all of its historical states. This is a more realistic and is one reason why fractional calculus has become more and more popular. On the other hand, the integer-order differential operator is indifferent to its history. Furthermore, there have been several recent mathematical discoveries that have helped to unlock the power of the fractional derivative [16]. One such discovery is that of fractal functions. Indeed, most of the functions that we are familiar with are smooth. This means that locally they can be approximated by a straight line segment. For example, the function  is well approximated by
is well approximated by  at the point
at the point  . The derivative of the function at a particular point provides the slope of the straight line approximation or tangent to the curve. Fractal functions are not smooth. They have details on all scales and they cannot be approximated locally by straight line segments. An example is the Weierstrass function which can be written as the infinite sum of cosine functions,
. The derivative of the function at a particular point provides the slope of the straight line approximation or tangent to the curve. Fractal functions are not smooth. They have details on all scales and they cannot be approximated locally by straight line segments. An example is the Weierstrass function which can be written as the infinite sum of cosine functions,  . For this function at the point
. For this function at the point  , the tangent changes orientation under increasing magnification. Functions such as the Weierstrass function cannot be differentiated (a whole number of times). But it turns out that these fractal functions can be differentiated a fractional number of times, and the fractional calculus is important for studying these differentiability properties. Fractals are characterized by scaling laws and the fractional derivative at a point can reveal this law. In recent research, scientists at the Mount Sinai School of Medicine have shown that the surfaces of breast cells are fractals and they have found clear differences in the scaling laws for benign cells and malignant cells. The different scaling laws have enabled accurate diagnosis of breast cancers. Another important new discovery that has brought fractional calculus into prominence is that many physical processes are modeled by fractional differential equations. Obviously, the importance of a mathematical model is that it can be used to make predictions and to give insight into the physical process that underlies the behavior. One area where mathematical models have been employed extensively is that of diffusion and transport processes. For example, the dispersion of pollutants in the ocean and the motion of electronic charges in conductors are diffusion processes. Here, a probabilistic description leads to a (whole number) differential equation which can be solved to predict average properties of the system. Similar types of equations are used by financial analysts to model stock prices. It has recently been discovered that processes governed by diffusion which is enhanced or hindered in some fashion are better modeled by FDEs than by integer-order differential equations. These FDEs are finding numerous applications in areas ranging from financial mathematics to ocean-atmosphere dynamics to mathematical biology [16].
, the tangent changes orientation under increasing magnification. Functions such as the Weierstrass function cannot be differentiated (a whole number of times). But it turns out that these fractal functions can be differentiated a fractional number of times, and the fractional calculus is important for studying these differentiability properties. Fractals are characterized by scaling laws and the fractional derivative at a point can reveal this law. In recent research, scientists at the Mount Sinai School of Medicine have shown that the surfaces of breast cells are fractals and they have found clear differences in the scaling laws for benign cells and malignant cells. The different scaling laws have enabled accurate diagnosis of breast cancers. Another important new discovery that has brought fractional calculus into prominence is that many physical processes are modeled by fractional differential equations. Obviously, the importance of a mathematical model is that it can be used to make predictions and to give insight into the physical process that underlies the behavior. One area where mathematical models have been employed extensively is that of diffusion and transport processes. For example, the dispersion of pollutants in the ocean and the motion of electronic charges in conductors are diffusion processes. Here, a probabilistic description leads to a (whole number) differential equation which can be solved to predict average properties of the system. Similar types of equations are used by financial analysts to model stock prices. It has recently been discovered that processes governed by diffusion which is enhanced or hindered in some fashion are better modeled by FDEs than by integer-order differential equations. These FDEs are finding numerous applications in areas ranging from financial mathematics to ocean-atmosphere dynamics to mathematical biology [16].
These and the other applications of FDEs provide a good motivation for study such Hilbert's 16th problem of system (1.2) in the form of FDE. So, in the next section we will consider system (1.2) in the form of FDEs and to be more specific we will take  ,
,  as polynomials of degree 1 and
as polynomials of degree 1 and  ,
,  as polynomials of degrees 3 and 5, respectively. Due to the existence of Riemann-Liouville integral operator in the definition of FDE in the Caputo sense [17], direct analytical solution for FDE is too rare, and so using the numerical methods is inevitable. In order to use a reliable numerical method we should first discretized the given FDE. However, discretization schemes that produce difference equations whose dynamics resemble that of their continuous counterparts are a major challenge in numerical analysis. To this end we will apply the Mickens nonstandard discretization scheme [18] to the Grunwald-Letnikov discretization process for our system of FDE. As we will see in Section 3 this discretization scheme leads to the fast convergence with more accurate results in solving the original system (1.2) with integer-order derivative one. Therefore, we are expecting the same accurate results for system (1.2) in the form of FDE with different noninteger-order derivative. Then in Section 4 we will discuss the stability of limit cycle which exists in our system and illustrate the numerical results. We will summarize the results with some final comments in Section 5.
as polynomials of degrees 3 and 5, respectively. Due to the existence of Riemann-Liouville integral operator in the definition of FDE in the Caputo sense [17], direct analytical solution for FDE is too rare, and so using the numerical methods is inevitable. In order to use a reliable numerical method we should first discretized the given FDE. However, discretization schemes that produce difference equations whose dynamics resemble that of their continuous counterparts are a major challenge in numerical analysis. To this end we will apply the Mickens nonstandard discretization scheme [18] to the Grunwald-Letnikov discretization process for our system of FDE. As we will see in Section 3 this discretization scheme leads to the fast convergence with more accurate results in solving the original system (1.2) with integer-order derivative one. Therefore, we are expecting the same accurate results for system (1.2) in the form of FDE with different noninteger-order derivative. Then in Section 4 we will discuss the stability of limit cycle which exists in our system and illustrate the numerical results. We will summarize the results with some final comments in Section 5.
2. Specific Case of the Weakened Hilbert's 16th Problem
We consider the specific case of system (1.2) as

where  , and
, and  are real constants. As discussed in [15] there is a closed relation between the number of the limit cycles in (2.1) and the number of zeros of its related Abelian integral [19]. The related Abelian integral of (2.1) stated as
are real constants. As discussed in [15] there is a closed relation between the number of the limit cycles in (2.1) and the number of zeros of its related Abelian integral [19]. The related Abelian integral of (2.1) stated as

where  is the area surrounded by the first integral curves of (2.1), that is,
is the area surrounded by the first integral curves of (2.1), that is,

as  and
and  . Now to evaluate the Abelian integral in (2.2), first we note that the limits of the double integrals can be found by solving the first integral (2.3) for y, that is,
. Now to evaluate the Abelian integral in (2.2), first we note that the limits of the double integrals can be found by solving the first integral (2.3) for y, that is,  and then for
and then for  by solving
by solving  when
when  , which yields
, which yields  with
with  . Hence, with the symmetry of
. Hence, with the symmetry of  which exists with respect to
which exists with respect to  and noting that
and noting that  , integral (2.2) yields
, integral (2.2) yields  . After evaluating and simplifying this equation as a polynomial of
. After evaluating and simplifying this equation as a polynomial of  , we get
, we get

Note that here we replace  where
where  . Finally, with this brief discussion the existence and stability of limit cycle for perturbed system (2.1) can be finalized in the following theorem.
. Finally, with this brief discussion the existence and stability of limit cycle for perturbed system (2.1) can be finalized in the following theorem.
Theorem 2.1.
The perturbed system (2.1) has no limit cycle for  and one limit cycle for
and one limit cycle for  . In the former case the unique limit cycle is stable for
. In the former case the unique limit cycle is stable for  and unstable for
and unstable for  .
.
For the proof of this theorem, as discussed above, we need to find the zero of the Abelian integral (2.4) which leads to a polynomial of degree 3 with respect to  . Then it is straight forward to see that this polynomial has no positive root for
. Then it is straight forward to see that this polynomial has no positive root for  and at least one positive real root for
and at least one positive real root for  . That is, in the first case system (2.1) has no limit cycle and in the former case there is one limit cycle. For the detail proof of this theorem refer to [15].
. That is, in the first case system (2.1) has no limit cycle and in the former case there is one limit cycle. For the detail proof of this theorem refer to [15].
3. System (2.1) in the Form of Fractional Differential Equations and Its Discretization
In general,  and
and  is a single initial value FDE, where
is a single initial value FDE, where  denotes the fractional derivative in the Caputo sense [17] and defined by
denotes the fractional derivative in the Caputo sense [17] and defined by  . Here
. Here  ,
,  and
and  is the
is the  -order Riemann-Liouville integral operator defined as
-order Riemann-Liouville integral operator defined as

with  A limited number of methods have been utilized to solve this initial value problem. In order to apply Mickens' nonstandard discretization scheme [18] in our numerical scheme we choose the Grunwald-Letnikov method to approximate the one-dimensional fractional derivative as follows [20]:
A limited number of methods have been utilized to solve this initial value problem. In order to apply Mickens' nonstandard discretization scheme [18] in our numerical scheme we choose the Grunwald-Letnikov method to approximate the one-dimensional fractional derivative as follows [20]:

where  denotes the integer part of
denotes the integer part of  and
and  is the step size. In this case the above initial value problem is discretized as
is the step size. In this case the above initial value problem is discretized as

where  and
and  are the Grunwald-Letnikov coefficients defined as
are the Grunwald-Letnikov coefficients defined as  , or recursively
, or recursively  and
and  .
.
Now using this definition for FDE with Grunwald-Letnikov discretization method, system (2.1) in the form of FDE is discretized as follows:

We assert that nonstandard discretization method is a numerical attempt which can be used in discretization process of FDE to get the better results and preserves their crucial property, that is, nonlocal property. In order to do this, we apply the Mickens nonstandard discretization scheme [18] to the Grunwald-Letnikov discretization process for FDE system (3.4). Indeed, the derivative term,  , in the Mickens schemes is replaced by
, in the Mickens schemes is replaced by  , where
, where  is a continuous function of step size
is a continuous function of step size  . In addition the nonlinear terms such as
. In addition the nonlinear terms such as  are either replaced by
are either replaced by  ,
,  or left untouched depending upon the context of the differential equation. There is no appropriate general method for choosing the function
or left untouched depending upon the context of the differential equation. There is no appropriate general method for choosing the function  , but some special techniques may be found in [18, 21].
, but some special techniques may be found in [18, 21].
Now we first write system (3.4) as follows:

Here, we replaced  and
and  by
by  and
and  , respectively. Later on, following Mickens' method in the next section, for finding the better results we replace the nonlinear terms in system (3.5) by appropriate combination of the variables in different levels of times.
, respectively. Later on, following Mickens' method in the next section, for finding the better results we replace the nonlinear terms in system (3.5) by appropriate combination of the variables in different levels of times.
4. Stability of the Limit Cycles in System (3.5) and Numerical Results
First we note that the linearized system (3.5), around a stationary point  or simply
or simply  , will be
, will be  where matrix
where matrix  is evaluated as
is evaluated as

Without losing our generality, we suppose here  to be positive. Now, from theory of dynamical systems, the limit cycle exists in system (3.5) whenever the characteristic equation of matrix,
to be positive. Now, from theory of dynamical systems, the limit cycle exists in system (3.5) whenever the characteristic equation of matrix, , has two solutions with module one.
, has two solutions with module one.
In addition, for the stability of this limit cycle we can use the stability analysis which is thoroughly investigated by Matignon in [22]. To utilize this theorem for our problem, first we consider the linearization of system (2.1) in the form of FDE with the derivative order  in both equations around a given stationary point
in both equations around a given stationary point  . This linearized system can be written as
. This linearized system can be written as  where matrix
where matrix  is similar to matrix
is similar to matrix  in (4.1) with
in (4.1) with  and
and  . Now the Matignon stability theorem for our problem can be stated as the following theorem.
. Now the Matignon stability theorem for our problem can be stated as the following theorem.
Theorem 4.1.
The linearized system of fractional differential equations  is asymptotically stable if and only if
is asymptotically stable if and only if  .
.
Note that the stability exists if and only if either asymptotically stability exists or those eigenvalues which satisfy  have geometric multiplicity one.
have geometric multiplicity one.
Now we will implement our numerical method described above for the existence of limit cycles in system (2.1) in the form of FDE for different values of fractional order  . In order to be consistence with the results in [15], in system (3.5) we let the constants
. In order to be consistence with the results in [15], in system (3.5) we let the constants  ,
,  be one and choose
be one and choose  ,
,  according to the following discussion with
according to the following discussion with  . By these assumptions characteristic equation of matrix
. By these assumptions characteristic equation of matrix  in (4.1) at the point (1, 1) will be
in (4.1) at the point (1, 1) will be

which yields

Equation (4.3) has two solutions with modular one if

First, we note that for  the inequality and equality occur in (4.4) if
the inequality and equality occur in (4.4) if  . That is, for some choice of
. That is, for some choice of  and
and  with opposite signs there is a limit cycle for system (3.5). This result agrees with the consequence of Theorem 2.1. Suppose that we choose
with opposite signs there is a limit cycle for system (3.5). This result agrees with the consequence of Theorem 2.1. Suppose that we choose  and
and  ; then the numerical solutions results of system (3.5) are illustrated in Figure 1. As we stated before, in order to get the better results in solving this system, following Mickens' method, we replace nonlinear terms
; then the numerical solutions results of system (3.5) are illustrated in Figure 1. As we stated before, in order to get the better results in solving this system, following Mickens' method, we replace nonlinear terms  , and
, and  with
with  ,
,  , and
, and  , respectively. Note that, given
, respectively. Note that, given  ,
,  , and
, and  from conditions (4.4) we can evaluate the best choice for
from conditions (4.4) we can evaluate the best choice for  (or
(or  ). Here, we get
). Here, we get  .
.
For the stability of this limit cycle, since  , by the well-known theories of dynamical systems we should find the eigenvalues of the linearized system (2.1) at the given point (1,1). In this case, with the choice of the above parameters, these eigenvalues are
, by the well-known theories of dynamical systems we should find the eigenvalues of the linearized system (2.1) at the given point (1,1). In this case, with the choice of the above parameters, these eigenvalues are  . Obviously, since the signs of real parts of
. Obviously, since the signs of real parts of  and
and  are negative, the limit cycle in Figure 1 is stable. With similar discussion, if we choose
are negative, the limit cycle in Figure 1 is stable. With similar discussion, if we choose  to be a positive constant, say 2, then the related eigenvalues will be
to be a positive constant, say 2, then the related eigenvalues will be  with the positive real parts. In this case, as we can see in Figure 2, the limit cycle is unstable. These results agree with consequence of Theorem 2.1.
with the positive real parts. In this case, as we can see in Figure 2, the limit cycle is unstable. These results agree with consequence of Theorem 2.1.
Now for the fractional order  , say
, say  , with the same values as above for
, with the same values as above for  ,
,  and
and  , conditions (4.4) are satisfied. So by these values of the parameters, there is a limit cycle for the system (3.5). As illustrated in Figures 2, 3, 4, and 5 these limit cycles exist for different values of
, conditions (4.4) are satisfied. So by these values of the parameters, there is a limit cycle for the system (3.5). As illustrated in Figures 2, 3, 4, and 5 these limit cycles exist for different values of  . For the stability of these limit cycles we may apply Theorem 4.1. For example, for
. For the stability of these limit cycles we may apply Theorem 4.1. For example, for  corresponding eigenvalues of matrix
corresponding eigenvalues of matrix  at the point
at the point  can be found as
can be found as  which yields
which yields  with argument
with argument  . Obviously, this value of
. Obviously, this value of  is beiger than
is beiger than  for
for  , which proves the stability of the limit cycles whenever exist.
, which proves the stability of the limit cycles whenever exist.
5. Final Comments
In this article we discussed the existence and stability of the limit cycle for special case of perturbed Hilbert's 16th problem. We found these limit cycles for different values of fractional order  using discretized system (3.5), provided by Grunwald-Letnikov numerical method for solving FDEs and applying Mickens' nonstandard method for more accurate results. The difficulties that we are facing here are in solving system (3.5) for values of
using discretized system (3.5), provided by Grunwald-Letnikov numerical method for solving FDEs and applying Mickens' nonstandard method for more accurate results. The difficulties that we are facing here are in solving system (3.5) for values of  . Though this is the case for different nonlinear systems of FDEs, existing numerical methods are not capable for solving such these systems for small fractional derivative order
. Though this is the case for different nonlinear systems of FDEs, existing numerical methods are not capable for solving such these systems for small fractional derivative order  . In other words, for the small efficient dimension, which is the sum of fractional derivatives of the equations in the systems such as system (2.1), the numerical results are not accurate enough. Here, for the values of
. In other words, for the small efficient dimension, which is the sum of fractional derivatives of the equations in the systems such as system (2.1), the numerical results are not accurate enough. Here, for the values of  with the same values for other parameters as above, the results are found by solving system (3.5) all converging to zero (see Figure 6).
with the same values for other parameters as above, the results are found by solving system (3.5) all converging to zero (see Figure 6).
Another difficulty exists in choosing  and
and  for conditions in (4.4) to be satisfied. That is, whenever
for conditions in (4.4) to be satisfied. That is, whenever  by choosing small positive values for
by choosing small positive values for  and
and  conditions (4.4) are satisfied, but the numerical limit cycle cannot be found in system (3.5) even in unstable form. Nevertheless, as we saw the limit cycles exist for the values
conditions (4.4) are satisfied, but the numerical limit cycle cannot be found in system (3.5) even in unstable form. Nevertheless, as we saw the limit cycles exist for the values  and
and  with different signs. In particular these limit cycles are stable, easy to find for values
with different signs. In particular these limit cycles are stable, easy to find for values  , and agreed with the stability condition in Theorem 4.1.
, and agreed with the stability condition in Theorem 4.1.
References
Gaiko VA: Hilbert's sixteenth problem and global bifurcations of limit cycles. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4455-4466. 10.1016/S0362-546X(01)00559-4
Gasull A, Giacomini H: A new criterion for controlling the number of limit cycles of some generalized Liénard equations. Journal of Differential Equations 2002,185(1):54-73. 10.1006/jdeq.2002.4172
Chen F, Li C, Llibre J, Zhang Z:A unified proof on the weak Hilbert 16th problem for
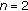 . Journal of Differential Equations 2006,221(2):309-342. 10.1016/j.jde.2005.01.009
. Journal of Differential Equations 2006,221(2):309-342. 10.1016/j.jde.2005.01.009Giné J: On some open problems in planar differential systems and Hilbert's 16th problem. Chaos, Solitons & Fractals 2007,31(5):1118-1134. 10.1016/j.chaos.2005.10.057
Du C, Liu Y: The problem of general center-focus and bifurcation of limit cycles for a planar system of nine degrees. Journal of Computational and Applied Mathematics 2009,223(2):1043-1057. 10.1016/j.cam.2008.03.037
Blows TR, Perko LM: Bifurcation of limit cycles from centers and separatrix cycles of planar analytic systems. SIAM Review 1994,36(3):341-376. 10.1137/1036094
Chow S-N, Li CZ, Wang D: Normal Forms and Bifurcation of Planar Vector Fields. Cambridge University Press, Cambridge, UK; 1994:viii+472.
Giacomini H, Llibre J, Viano M: On the nonexistence, existence and uniqueness of limit cycles. Nonlinearity 1996,9(2):501-516. 10.1088/0951-7715/9/2/013
Llibre J, Pérez del Río JS, Rodríguez JA: Averaging analysis of a perturbated quadratic center. Nonlinear Analysis: Theory, Methods & Applications 2001,46(1):45-51. 10.1016/S0362-546X(99)00444-7
Li C, Li W, Llibre J, Zhang Z: Polynomial systems: a lower bound for the weakened 16th Hilbert problem. Extracta Mathematicae 2001,16(3):441-447.
Coll B, Gasull A, Prohens R: Bifurcation of limit cycles from two families of centers. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2005,12(2):275-287.
Llibre J, Zhang X: On the number of limit cycles for some perturbed Hamiltonian polynomial systems. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2001,8(2):161-181.
García B, Llibre J, Pérez del Río JS: On the number of limit cycles surrounding a unique singular point for polynomial differential systems of arbitrary degree. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4461-4469. 10.1016/j.na.2007.11.004
Atabaigi A, Nyamoradi N, Zangeneh HRZ: The number of limit cycles of a quintic polynomial system. Computers & Mathematics with Applications 2009,57(4):677-684. 10.1016/j.camwa.2008.10.079
Atabaigi A, Nyamoradi N, Zangeneh HRZ: The number of limit cycles of a quintic Hamiltonian system with perturbation. Balkan Journal of Geometry and Its Applications 2008,13(2):1-11.
Borredon L, Henry B, Wearne S: Differentiating the non-differentiable fractional calculus. Parabola 1999,35(2):8-17.
Caputo M: Linear models of dissipation whose Q is almost frequency independent-II. Geophysical Journal of the Royal Astronomical Society 1967, 13: 529-539. 10.1111/j.1365-246X.1967.tb02303.x
Mickens RE: Nonstandard Finite Difference Models of Differential Equations. World Scientific, River Edge, NJ, USA; 1994:xii+249.
Ye YQ, Cai SL, Chen LS, et al.: Theory of Limit Cycles, Translations of Mathematical Monographs. Volume 66. 2nd edition. American Mathematical Society, Providence, RI, USA; 1986:xi+435.
Meerschaert MM, Tadjeran C: Finite difference approximations for fractional advection-dispersion flow equations. Journal of Computational and Applied Mathematics 2004,172(1):65-77. 10.1016/j.cam.2004.01.033
Liu P, Elaydi SN: Discrete competitive and cooperative models of Lotka-Volterra type. Journal of Computational Analysis and Applications 2001,3(1):53-73. 10.1023/A:1011539901001
Matignon D: Stability results of fractional differential equations with applications to control processing. Proceeding of the IMACS-IEEE Multiconference on Computational Engineering in Systems Applications (CESA '96), July 1996, Lille, France 963:
Acknowledgment
This work is supported by Qatar National Research Fund under the Grant no. NPRP08-056-1–014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Erjaee, G., Zangeneh, H. & Nyamoradi, N. Limit Cycles of a Class of Hilbert's Sixteenth Problem Presented by Fractional Differential Equations. Adv Differ Equ 2010, 938180 (2010). https://doi.org/10.1155/2010/938180
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/938180

 ,
,  ,
,  , and
, and  with starting point (1, 1).
with starting point (1, 1).
 , and
, and  with starting point (1, 1).
with starting point (1, 1).
 ,
, 
 , and
, and  with starting point (1, 1).
with starting point (1, 1).
 ,
,  ,
,  , and
, and  with starting point (1, 1).
with starting point (1, 1).
 ,
,  ,
,  , and
, and  with starting point (1, 1).
with starting point (1, 1).
 ,
,  ,
,  , and
, and  with starting point (1, 1).
with starting point (1, 1).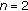 . Journal of Differential Equations 2006,221(2):309-342. 10.1016/j.jde.2005.01.009
. Journal of Differential Equations 2006,221(2):309-342. 10.1016/j.jde.2005.01.009