- Research Article
- Open access
- Published:
Nonlocal Conditions for Lower Semicontinuous Parabolic Inclusions
Advances in Difference Equations volume 2011, Article number: 109570 (2011)
Abstract
We discuss conditions for the existence of at least one solution of a discontinuous parabolic equation with lower semicontinuous right hand side and a nonlocal initial condition of integral type. Our technique is based on fixed point theorems for multivalued maps.
1. Introduction
Let  be an open bounded domain in
be an open bounded domain in  ,
,  , with a smooth boundary
, with a smooth boundary  . We denote the norm (usually the Euclidean norm) of
. We denote the norm (usually the Euclidean norm) of  by
by  . Let
. Let  be a positive real number. Set
be a positive real number. Set  and
and  . For
. For  we denote its partial derivatives (when they exist) by
we denote its partial derivatives (when they exist) by  .
.
Let  denote the Banach space of continuous functions
denote the Banach space of continuous functions  , endowed with the norm
, endowed with the norm

For  , we say that
, we say that  is in
is in  if
if  is measurable and
is measurable and  , in which case we define its norm by
, in which case we define its norm by

Consider the linear nonhomogeneous problem


with the following nonlocal initial condition:

Here,  is an elliptic operator given by
is an elliptic operator given by

We will assume throughout this paper that the functions  are Hölder continuous,
are Hölder continuous,  , and moreover, there exist positive numbers
, and moreover, there exist positive numbers  such that
such that

Let  be continuous. For the problem (1.3), (1.4) together with initial condition
be continuous. For the problem (1.3), (1.4) together with initial condition

we have the following classical result.
Assume that the function  is Hölder continuous on
is Hölder continuous on  and
and  is continuous on
is continuous on  . Then problem (1.3), (1.4), (1.8) has a unique solution
. Then problem (1.3), (1.4), (1.8) has a unique solution  , which for each
, which for each  , is given by
, is given by

where  , is the Green's function corresponding to the linear homogeneous problem. This function has the following properties (see [1, 4]).
, is the Green's function corresponding to the linear homogeneous problem. This function has the following properties (see [1, 4]).
-
(i)
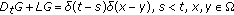 .
. -
(ii)
 .
. -
(iii)
 .
. -
(iv)
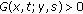 for
for  .
. -
(v)
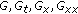 are continuous functions of
are continuous functions of  .
.In addition to the above,
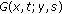 satisfies the following important estimate.
satisfies the following important estimate. -
(vi)
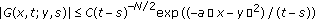 , for some positive constants
, for some positive constants  (see [2]).
(see [2]).
Since  , it is clear that the functions
, it is clear that the functions  and
and  are continuous. Let
are continuous. Let 
 and let
and let  Also, property (vi) above shows that
Also, property (vi) above shows that  .
.
In this paper, we consider a nonlocal problem for a class of nonlinear parabolic equations with a lower semicontinuous multivalued right hand side. More specifically, we consider the following problem,

Parabolic problems with discontinuous nonlinearities arise as simplified models in the description of porous medium combustion [5], chemical reactor theory [6]. Also, best response dynamics arising in game theory can be modeled by a parabolic equation with a discontinuous right hand side [7, 8]. Parabolic problems with discontinuous nonlinearities have been also investigated in the papers [9–13]. On the other hand, parabolic problems with integral boundary conditions appear in the modeling of concrete problems, such as heat conduction [14, 15] and thermoelasticity [16]. Also, the importance of nonlocal conditions and their applications in different field has been discussed in [17, 18]. Several papers have been devoted to the study of parabolic problems with integral conditions [19, 20]. Next, we state some important facts about multivalued functions and results that will be used in the remainder of the paper.
A subset  is
is  measurable if
measurable if  belongs to the
belongs to the  -algebra generated by all sets of the form
-algebra generated by all sets of the form  where
where  is Lebesgue measurable in
is Lebesgue measurable in  and
and  is Borel measurable in
is Borel measurable in  . Let
. Let  and
and  be Banach spaces.
be Banach spaces.  denotes the set of all nonempty subsets of
denotes the set of all nonempty subsets of  . The domain of a multivalued map
. The domain of a multivalued map  is the set Dom(
is the set Dom( has closed values if
has closed values if  is a closed subset of
is a closed subset of  for each
for each  and we write
and we write  . Also,
. Also,  denotes the set of all nonempty closed and convex subsets of
denotes the set of all nonempty closed and convex subsets of  .
.  is bounded if
is bounded if  is called lower semicontinuous (lsc) on
is called lower semicontinuous (lsc) on  if
if  is open in
is open in  whenever
whenever  is open in
is open in  , or the set
, or the set  is closed in
is closed in  whenever
whenever  is closed in
is closed in  . For more details on multivalued maps, we refer the interested reader to the books [21–24].
. For more details on multivalued maps, we refer the interested reader to the books [21–24].
Let  denote the Kuratowski measure of noncompactness. See [25] for definitions and details.
denote the Kuratowski measure of noncompactness. See [25] for definitions and details.
Theorem 1.2 (see [26, Theorem 3.1]).
Let  be a separable Banach space. Assume the following conditions hold. There exists
be a separable Banach space. Assume the following conditions hold. There exists  , independent of
, independent of  , with
, with  for any solution
for any solution  to
to  a.e. on
a.e. on  for each
for each  is a closed map,
is a closed map,  is a bounded subset of
is a bounded subset of  , and
, and  for all
for all  with strict inequality if
with strict inequality if  . Then the inclusion
. Then the inclusion  has a solution
has a solution  .
.
2. Main Result
By a solution of problem (1.10), (7), (8) we mean a function  such that there exists a function
such that there exists a function  with
with  for each
for each  and (1.3), (1.4), (1.5) hold.
and (1.3), (1.4), (1.5) hold.
Theorem 2.1.
Assume that the following conditions are satisfied.
(HF) is
is  measurable,
measurable,  is lsc for a.e.
is lsc for a.e. , there exist
, there exist  such that
such that  with 2Vol
with 2Vol and there exists
and there exists 
 such that
such that  for any bounded set
for any bounded set  ,
,
(Hk) is continuous, bounded and there exists
is continuous, bounded and there exists  such that
such that  .
.
Then problem (1.10), (7), (8) has a solution provided that  .
.
Proof.
We shall follow the ideas developed in [27]. It follows from the integral representation (1.9) that any solution  of (1.10), (7), (8) is a solution of the operator inclusion
of (1.10), (7), (8) is a solution of the operator inclusion

for  , where
, where

where  is given by
is given by

while  is given by
is given by

First, we show that solutions of (2.1) are a priori bounded. We have

where  , that is
, that is  for each
for each  . Since
. Since  is bounded there exists
is bounded there exists  such that
such that 
 . It follows from the properties of the Green's function and the assumption (HF) that
. It follows from the properties of the Green's function and the assumption (HF) that

Hence

Equation (2.7) implies that

or

Therefore, there exists  , independent of
, independent of  , but depending on
, but depending on  and the Green's function such that any possible solution of (2.1) satisfies
and the Green's function such that any possible solution of (2.1) satisfies

Let  . Then
. Then  is nonempty, closed, and bounded subset of
is nonempty, closed, and bounded subset of  .
.
Since the multifunction  has nonempty, closed and convex values, it follows that
has nonempty, closed and convex values, it follows that  has nonempty, closed, and convex values. Since
has nonempty, closed, and convex values. Since  is a continuous single valued operator, it is clear that
is a continuous single valued operator, it is clear that  has nonempty, closed, and convex values. Next, we can easily show that
has nonempty, closed, and convex values. Next, we can easily show that  is a closed map (i.e., has a closed graph) and
is a closed map (i.e., has a closed graph) and  is a bounded subset of
is a bounded subset of  .
.
Finally, we show that  for any bounded subset
for any bounded subset  . So, let
. So, let  . Then, since
. Then, since  , we have
, we have

Hence

It follows from the assumption that

This shows that  is a condensing multivalued map.
is a condensing multivalued map.
By Theorem 3.1 in [26],  has a fixed point in
has a fixed point in  , which is a solution of problem (1.10), (7), (8). This completes the proof of the main result.
, which is a solution of problem (1.10), (7), (8). This completes the proof of the main result.
References
Friedman A: Partial Differential Equations of Parabolic Type. Prentice-Hall, Englewood Cliffs, NJ, USA; 1964:xiv+347.
Ladyzhenskaya OA, Solonnikov VA, Uraltseva NN: Linear and Quasilinear Equations of Parabolic Type. Nauka, Moscow, Russia; 1967. English translation: American Mathematical Society, Providence, RI, USA, 1968
Lieberman GM: Second Order Parabolic Di¤erential Equations. World Scientific, River Edge, NJ, USA; 1996:xii+439.
Pao CV: Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York, NY, USA; 1992:xvi+777.
Feireisl E, Norbury J: Some existence, uniqueness and nonuniqueness theorems for solutions of parabolic equations with discontinuous nonlinearities. Proceedings of the Royal Society of Edinburgh A 1991,119(1-2):1-17. 10.1017/S0308210500028262
Fleishman BA, Mahar TJ: A step-function model in chemical reactor theory: multiplicity and stability of solutions. Nonlinear Analysis 1981,5(6):645-654. 10.1016/0362-546X(81)90080-8
Deguchi H: On weak solutions of parabolic initial value problems with discontinuous nonlinearities. Nonlinear Analysis, Theory, Methods and Applications 2005,63(5–7):e1107-e1117.
Hofbauer J, Simon PL:An existence theorem for parabolic equations on
 with discontinuous nonlinearity. Electronic Journal of Qualitative Theory of Differential Equations 2001, (8):-9.
with discontinuous nonlinearity. Electronic Journal of Qualitative Theory of Differential Equations 2001, (8):-9.Cardinali T, Fiacca A, Papageorgiou NS: Extremal solutions for nonlinear parabolic problems with discontinuities. Monatshefte für Mathematik 1997,124(2):119-131. 10.1007/BF01300615
Carl S, Grossmann Ch, Pao CV: Existence and monotone iterations for parabolic differential inclusions. Communications on Applied Nonlinear Analysis 1996,3(1):1-24.
Carl S, Heikkilä S: On a parabolic boundary value problem with discontinuous nonlinearity. Nonlinear Analysis: Theory, Methods & Applications 1990,15(11):1091-1095. 10.1016/0362-546X(90)90156-B
Pisani R: Problemi al contorno per operatori parabolici con non linearita discontinua. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 1982, 14: 85-98.
Rauch J: Discontinuous semilinear differential equations and multiple valued maps. Proceedings of the American Mathematical Society 1977,64(2):277-282. 10.1090/S0002-9939-1977-0442453-6
Cannon JR: The solution of the heat equation subject to the specification of energy. Quarterly of Applied Mathematics 1963, 21: 155-160.
Ionkin NI: Solution of a boundary value problem in heat conduction theory with nonlocal boundary conditions. Differential Equations 1977, 13: 204-211.
Day WA: A decreasing property of solutions of parabolic equations with applications to thermoelasticity. Quarterly of Applied Mathematics 1983,40(4):468-475.
Balachandran K, Uchiyama K: Existence of solutions of nonlinear integrodifferential equations of Sobolev type with nonlocal condition in Banach spaces. Proceedings of the Indian Academy of Sciences 2000,110(2):225-232. 10.1007/BF02829493
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. Journal of Mathematical Analysis and Applications 1991,162(2):494-505. 10.1016/0022-247X(91)90164-U
Dai D-Q, Huang Y: Remarks on a semilinear heat equation with integral boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2007,67(2):468-475. 10.1016/j.na.2006.06.012
Olmstead WE, Roberts CA: The one-dimensional heat equation with a nonlocal initial condition. Applied Mathematics Letters 1997,10(3):89-94. 10.1016/S0893-9659(97)00041-4
Aubin J-P, Cellina A: Differential Inclusions. Springer, Berlin, Germany; 1984:xiii+342.
Aubin J-P, Frankowska H: Set-Valued Analysis, Systems & Control: Foundations & Applications. Volume 2. Birkhäuser, Boston, Mass, USA; 1990:xx+461.
Deimling K: Multivalued Differential Equations, de Gruyter Series in Nonlinear Analysis and Applications. Volume 1. Walter de Gruyter, Berlin, Germany; 1992:xii+260.
Hu S, Papageorgiou NS: Handbook of Multivalued Analysis, Vol. I: Theory, Mathematics and Its Applications. Volume 419. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000.
Kamenskii M, Obukhovskii V, Zecca P: Condensing Multivalued Maps and Semilinear Differential Inclusions in Banach Spaces, de Gruyter Series in Nonlinear Analysis and Applications. Volume 7. Walter de Gruyter, Berlin, Germany; 2001:xii+231.
Agarwal RP, O'Regan D: Existence criteria for operator inclusions in abstract spaces. Journal of Computational and Applied Mathematics 2000,113(1-2):183-193. 10.1016/S0377-0427(99)00252-6
Byszewski L, Papageorgiou NS: An application of a noncompactness technique to an investigation of the existence of solutions to a nonlocal multivalued Darboux problem. Journal of Applied Mathematics and Stochastic Analysis 1999,12(2):179-190. 10.1155/S1048953399000180
Acknowledgments
This work is part of an ongoing research project FT090001. The author is grateful to KFUPM for its constant support. The author would like to thank an anonymous referee for his/her comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boucherif, A. Nonlocal Conditions for Lower Semicontinuous Parabolic Inclusions. Adv Differ Equ 2011, 109570 (2011). https://doi.org/10.1155/2011/109570
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/109570
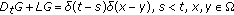 .
. .
. .
.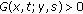 for
for  .
.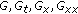 are continuous functions of
are continuous functions of  .
.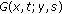 satisfies the following important estimate.
satisfies the following important estimate.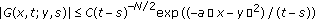 , for some positive constants
, for some positive constants  (see [
(see [ with discontinuous nonlinearity. Electronic Journal of Qualitative Theory of Differential Equations 2001, (8):-9.
with discontinuous nonlinearity. Electronic Journal of Qualitative Theory of Differential Equations 2001, (8):-9.