Bifurcation of limit cycles from a hyper-elliptic Hamiltonian system with a double heteroclinic loops

Abstract

In this article, we consider the Liénard system of the form

$$\dot{x}=y,\dot{y}=x(x-1)(x+1)(x^2-3)+\epsilon (\alpha +\beta x^2+\gamma x^4)y$$

with $0<\epsilon \ll 1$, a, b and c are real bounded parameters. We prove that the least upper bound of the number of isolated zeros of the corresponding Abelian integral

$$I(h)={\oint }_{{\mathrm{\Gamma }}_h}(\alpha +\beta x^2+\gamma x^4)ydx$$

is four (counting the multiplicity). This implies that the number of limit cycles that bifurcated from periodic orbits of the unperturbed system for $\epsilon =0$ is less than or equal to four.

MSC:34C05, 34C07, 34C08.

1 Introduction

Let $H(x,y)$, $p(x,y)$ and $q(x,y)$ be polynomials of x and y, and suppose that $deg(H)=n+1$ and $max\{def(p),deg(q)\}=n$. $H(x,y)$ defines at least one family of closed curves (or ovals) $L_h$, where h is a parameter on an open interval J. Then $\omega =q(x,y)dx-p(x,y)dy$ is called 1-form of degree n and the so-called Abelian integral (also called a first-order Melnikov function) defined on all ovals of $H(x,y)$ is as follows:

$$A(h)={\oint }_{{\mathrm{\Gamma }}_h}\omega ,h\in J.$$

(1.1)

For a given n, which is the maximal number of zeros of $A(h)$, this is the famous weak Hilbert’s 16th problem proposed by Arnold in 1977. It is well known that this problem is very difficult and still remains unresolved, its research advance and the recent popular and efficient method for special Abelian integral (1.1) can be found in the summary works [1, 2]. Using the above $H(x,y)$, $p(x,y)$ and $q(x,y)$, we can obtain the following system:

$$\dot{x}=H_y+\epsilon p(x,y,\delta ),\dot{y}=-H_x+\epsilon q(x,y,\delta ),$$

(1.2)

which is called a near-Hamiltonian system, ε is a small positive parameter. Taking $\epsilon =0$, we obtain the corresponding Hamiltonian system

$$\dot{x}=H_y,\dot{y}=-H_x.$$

(1.3)

The closed curves $L_h$ correspond to the periodic orbits of system (1.3) which form the annulus of system (1.3). If $A(h)$ is not identically zero, the number of zeros of $A(h)$ provides an upper bound of the number of limit cycles of (1.2) bifurcated from the periodic annulus of (1.3) by the Poincaré-Pontryagin theorem [3]. Therefore, system (1.2) is also an important and main research system in the second part of Hilbert’s 16th problem which asks for the maximum number and position of limit cycles for polynomial planar vector fields depending on the degree of the vector field. However, it is still an open problem to find the maximum number of limit cycles even for quadratic systems; see a recent summary work [4] for its research advance.

In the progress to solve the weak Hilbert’s 16th problem and the second part of Hilbert’s 16th problem, many mathematicians are more interested in the following special near-Hamiltonian system that is called the Liénard system:

$$\dot{x}=y,\dot{y}=g(x)+\epsilon f(x)y$$

(1.4)

of type $(m,n)$, where $g(x)$ and $f(x)$ are polynomials of degree, respectively, m and n, ε is positive and very small, and the corresponding Hamiltonian function is as follows:

$$H(x,y)=\frac{y^2}{2}-\int g(x)dx.$$

When the degree of $H(x,y)$ is three or four, system (1.4) is of elliptic Hamiltonian systems,when the degree of $H(x,y)$ is more than five, (1.4) is of hyperelliptic Hamiltonian systems. A comprehensive study has been made in [5] for the cases $m+n\le 4$, except for $(m,n)=(1,3)$. In all these cases, it has been proven that at most one limit cycle can appear, and for $(m,n)=(1,3)$, the same result has been conjectured (see [6]).

Taking $g(x)$ is a polynomial of degree three and $f(x)=a+bx+c{x}^2$, system (1.4) is of type $(3,2)$, there are several cases according to the portraits of the unperturbed system. Dumortier and Li [7–10] have made a complete study on these cases and obtained different sharp upper bounds of the number of zeros of Abelian integrals for different cases. Li, Pavao and Roussarieb [11] investigated some Liénard systems of type $(3,2)$ with symmetry and also obtained their sharp bound of the corresponding Abelian integral. For the type $(4,3)$, Wang and Xiao [12] have investigated some Liénard system of type $(4,3)$, combined with the PhD thesis [13]. They have proved that four is the least upper bound and three is maximum lower bound of the number of zeros for the corresponding Abelian integral. The results of the maximum lower bound of the number of zeros for the Abelian integral corresponding to this kind system can be found in [14–16].

For the type $(5,4)$, mathematicians have studied the following Liénard systems with symmetry of the form

$$\dot{x}=y,\dot{y}=\eta x(x^2-a)(x^2-b)+\epsilon (\alpha +\beta x^2+\gamma x^4)y,$$

(1.5)

where $\eta =\pm 1$, α, β and γ are real bounded numbers. Without loss of generality, we assume $b\ge a\ge 0$. When the portraits of system (1.5) with $\epsilon =0$ have at least one periodic annulus surrounding an element center, there are several cases according to the value of a and b; see Figure 1.

Figure 1

Six cases for ( 1.5 ) have at least one annulus surrounding an elementary center.

For case 1, Asheghi and Zangeneh [17] studied (1.5) by taking $a=0$, $b=1$ and proved that the corresponding Abelian integral has at most two zeros inside the double cuspidal loop. For case 2, Qi and Zhao [18] proved that system (1.5) with $a=\frac{21-\sqrt{41}}{20}$ and $b=\frac{21+\sqrt{41}}{20}$ has at most two limit cycles bifurcated from each annulus. For case 4, Xu and Li [19] proved that system (1.5) has at least five limit cycles bifurcated from three annuluses of system (1.5) with $a=\frac{1}{4}$, $b=1$. For case 5, Zhang et al. [20] proved that system (1.5) with $a=\frac{1}{2}$, $b=2$ has at most three limit cycles bifurcated from the annuluses. For case 6, Asheghi and Zangeneh studied (1.5) with $a=b=1$ and proved that the least upper bound for the number of zeros of the related Abelian integral inside the eye-figure loop is two in [21] and both inside and outside the eye-figure loop is four in [22].

In this article, we study case 3 by a very new algebra method. Without loss of generality, we take $\eta =1$, $a=1$, $b=3$, then system (1.5) becomes

$$\dot{x}=y,\dot{y}=x(x^2-1)(x^2-3)+\epsilon (\alpha +\beta x^2+\gamma x^4)y,$$

(1.6)

with the Hamiltonian function of the unperturbed system

$$\tilde{H}(x,y)=\frac{y^2}{2}-\frac{3}{2}{x}^2+x^4-\frac{1}{6}{x}^6.$$

(1.7)

The level sets (i.e., $\tilde{H}(x,y)=h$) of Hamiltonian function (1.7) are sketched in Figure 2. It is easy to check $\tilde{H}(x,y)=h$ defines two families of ovals with symmetry which correspond to two symmetric period annuluses that consist of closed clockwise orbits of system (1.6) denoted by ${\mathrm{\Gamma }}_h$. $H(x,y)=0$ defines two symmetric 2-polycycles ${\mathrm{\Gamma }}^1=\{(x,y)|H(x,y)=0,x>0\}$ and ${\mathrm{\Gamma }}^2=\{(x,y)|H(x,y)=0,x<0\}$ which are formed by heteroclinic orbits.

Figure 2

The level set of $\tilde{\mathit{H}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ .

On the right half-plane, the closed orbits ${\mathrm{\Gamma }}_h$ inside ${\mathrm{\Gamma }}^1$ are defined by

$${\mathrm{\Gamma }}_h=\{(x,y)|\tilde{H}(x,y)=h,h\in (-\frac{2}{3},0)\},$$

${\mathrm{\Gamma }}_h$ shrinks to the center $C(1,0)$ defined by $H(x,y)=-\frac{2}{3}$ when $h\to -{\frac{2}{3}}^{+}$, ${\mathrm{\Gamma }}_h$ expands to the 2-polycycles ${\mathrm{\Gamma }}^1$ when $h\to 0^{-}$. The Abelian integral on ${\mathrm{\Gamma }}_h$ of the right half-plane is as follows:

$$I(h,\delta )={\oint }_{{\mathrm{\Gamma }}_h}(\alpha +\beta x^2+\gamma x^4)ydx\equiv \alpha I_0(h)+\beta I_1(h)+\gamma I_2(h)$$

(1.8)

for $h\in (-\frac{2}{3},0)$, where $\delta =(\alpha ,\beta ,\gamma )$, $I_i(h)={\oint }_{{\mathrm{\Gamma }}_h}{x}^{2i}ydx$, $i=0,1,2$. By symmetry, we can only investigate the right half-plane. Without loss of generality, we fix $\gamma =1$ and obtain the following main results.

Theorem A For all α and β, the least upper bound of the number of zeros of the Abelian integral $I(h,\delta )$ is two (counting the multiplicity) for $h\in (-\frac{2}{3},0)$ with ${\mathrm{\Gamma }}_h$ inside one saddle polycycle ${\mathrm{\Gamma }}^i$ for $i=1,2$. System (1.6) has at most two limit cycles bifurcated from each period annulus and at most four limit cycles from the two period annuluses.

The rest of the article is organized as follows. In Section 2, we introduce some definitions and the new criteria which are used to determine the number of zeros of the Abelian integral $I(h,\delta )$. In Section 3, we prove the main result.

2 Preliminary lemmas and definitions

The method we introduce proposes some criterion functions defined directly by Hamiltonian and integrands of Abelian integrals, through which the problem whether the basis of the vector space generated by an Abelian integral is a Chebyshev system could be reduced to the problem whether the family of criterion functions form a Chebyshev system, since the latter can be tackled by checking the non-vanishing properties of its Wronskians. For this paper to be self-contained, we list some related definitions and criterions. For more details, refer to [23, 24].

Definition 2.1 Suppose $f_0,f_1,f_2,\dots ,f_{n-1}$ are analytic functions on a real open interval J.

• (i) The family of sets $\{f_0,f_1,f_2,\dots ,f_{n-1}\}$ is called a Chebyshev system (T-system for short) provided that any nontrivial linear combination

  $$k_0{f}_0(x)+k_1{f}_1(x)+\cdots +k_{n-1}{f}_{n-1}(x)$$

has at most $n-1$ isolated zeros on J.

• (ii) An ordered set of n functions $\{f_0,f_1,f_2,\dots ,f_{n-1}\}$ is called a complete Chebyshev system (CT-system for short) provided any nontrivial linear combination $k_0{f}_0(x)+k_1{f}_1(x)+\cdots +k_{i-1}{f}_{i-1}(x)$ has at most $i-1$ zeros for all $i=1,2,\dots ,n$. Moreover, it is called an extended complete Chebyshev system (ECT-system for short) if the multiplicities of zeros are taken into account.

• (iii) The continuous Wronskian of $\{f_0,f_1,f_2,\dots ,f_{n-1}\}$ at $x\in R$ is

  

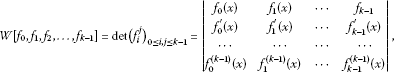
where $f^{\prime }(x)$ is the first-order derivative of $f(x)$ and $f^{(i)}(x)$ is the i th-order derivative of $f(x)$, $i\ge 2$. The definitions imply that the function tuple $\{f_0,f_1,\dots ,f_{k-1}\}$ is an ECT-system on J, therefore it is a CT-system on J, and then a T-system on J; however, the inverse implications are all not true.

Recall that the authors of [24] studied the number of isolated zeros of Abelian integrals in a purely algebraic criteria which are developed from the idea introduced in [25]. Let $H(x,y)=A(x)+\frac{1}{2}{y}^2$ be an analytic function in some open subset of the plane that has a local minimum at $(x_0,0)$. Then there exists a punctured neighborhood P of the origin foliated by ovals $L_h=H(x,y)=h$ which correspond to the clockwise closed orbits of (1.3). The set of ovals $L_h$ inside the period annulus is parameterized by the energy levels $h\in (h_1,h_2)=J$ for some $h_i\in (0,+\mathrm{\infty }]$. The projection of P on the x-axis is an interval $(x_l,x_r)$ with $x_l<x_0<x_r$. Under the above assumptions, it is easy to verify that $x{A}^{\prime }(x)>0$ for all $x\in (x_l,x_r)\setminus \{x_0\}$. Then $A(x)$ has a zero of even multiplicity at $x=x_0$, and so there exists an analytic involution $z(x)$ such that

$$A(x)=A(z(x))$$

for all $x\in (x_l,x_r)$.

For the number of isolated zeros of nontrivial linear combination of some Abelian integrals, the algebraic criterion in [24] (Theorem B) can be stated as follows.

Lemma 2.1 Assume that function $f_i(x)$ is analytic on the interval $(x_l,x_r)$ for $i=0,1,\dots ,n-1$, and considering

$$A_i(h)={\int }_{L_h}{f}_i(x)y^{2s-1}dx,i=0,1,\dots ,n-1,$$

where for each $h\in (0,h_0)$, $L_h$ is the oval surrounding the origin inside the level curve $\{A(x)+\frac{1}{2}{y}^{2m}=h\}$, we define

$$l_i(x):=\frac{f_i(x)}{A^{\prime }(x)}-\frac{f_i(z(x))}{A^{\prime }(z(x))}.$$

Then $\{A_0,A_1,\dots ,A_{n-1}\}$ is an extended complete Chebyshev system on $(h_1,h_2)$ if $\{l_0,l_1,\dots ,l_{n-1}\}$ is a complete Chebyshev system on $(x_l,x_0)$ or $(x_0,x_r)$ and $s>(n-2)$. And $\{l_0,l_1,\dots ,l_{n-1}\}$ is an ECT-system on $(x_0,x_r)$ or $(x_l,x_0)$ if and only if the continuous Wronskian of $\{l_0,l_1,\dots ,l_{k-1}\}$ does not vanish for $x\in (x_0,x_r)$ or for $z\in (x_l,x_0)$ and $k=1,\dots ,n$.

Usually s is not big enough ($s>n-2$ does not hold), we cannot apply Lemma 2.1 directly. To overcome this problem, we can use the following result (see [24], Lemma 4.1) to increase the power of y in $A_i(h)$.

Lemma 2.2 Let $L_h$ be an oval inside the level curve $A(x)+\frac{1}{2}(x)y^2=h$ and consider a function $F(x)$ such that $\frac{F(x)}{A^{\prime }(x)}$ is analytic at $x=0$. Then for any $k\in N$,

$${\oint }_{L_h}F(x)y^{k-2}dx={\oint }_{L_h}G(x)y^{k}dx,$$

where $G(x)=\frac{1}{k}{(\frac{F}{A^{\prime }})}^{\prime }(x)$.

3 Proof of the main result

In what follows, we shall apply Lemma 2.1 to study if Abelian integrals

$$I_i(h)={\int }_{{\mathrm{\Gamma }}_h}{x}^{2i}ydx,i=0,1,2$$

have the Chebyshev property in the interval $(-\frac{2}{3},0)$. Following the notation in Lemma 2.1, we have $A(x)=\tilde{H}(x,0)=-\frac{3}{2}{x}^2+x^4-\frac{1}{6}{x}^6$, and $s=1$, $n=3$. The period annulus is foliated by the ovals ${\mathrm{\Gamma }}_h$, and the projection of the period annulus on the right half-plane is an open interval $(0,\sqrt{3})$ satisfying $A(0)=A(\sqrt{3})$. Noting that $x{A}^{\prime }(x)>0$ for all $x\in (0,\sqrt{3})\setminus \{1\}$, therefore there exists an analytic involution $z(x)$ as $0<x<1$ and $1<z(x)<\sqrt{3}$ such that

$$A(x)=A(z(x))$$

as $0<x<1$, the involution is represented in Figure 3.

Figure 3

The involution $\mathit{z}\mathbf{(}\mathit{x}\mathbf{)}$ defined by $\mathit{A}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{=}\mathit{A}\mathbf{(}\mathit{z}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{)}$ .

Our goal is to prove that the vector space generated by an Abelian integral $I_i(h)$ has the Chebyshev property for $x\in (0,\sqrt{3})$ by Lemma 2.1. However, note that $s=1$ and $n=3$, which does not satisfy the hypothesis $s>n-2$ in Lemma 2.1. Thus, we have to promote the power s of y in the integrand of $I_i(h)$ such that the condition $s>n-2$ holds.

Lemma 3.1 For $i=0,1,2$, we have

$$2h{I}_i(h)={\int }_{{\mathrm{\Gamma }}_h}{f}_i(x)y^{3}dx,$$

where $f_i(x)=\frac{2}{9}\frac{x^{2i}{\tilde{f}}_i(x)}{{(x-1)}^2{(x+1)}^2}$ and ${\tilde{f}}_i(x)=5x^4-9x^2+6+i{x}^4-4i{x}^2+3i$.

Proof It is clear that on every periodic orbit ${\mathrm{\Gamma }}_h=\{\tilde{H}(x,y)=h\}$, $\frac{2A(x)+y^2}{2h}=1$ holds, therefore

$$\begin{array}{rl}{I}_i(h)& =\frac{1}{2h}{\int }_{{\mathrm{\Gamma }}_h}(2A(x)+y^2)x^{2i}ydx\\ =\frac{1}{2h}{\int }_{{\mathrm{\Gamma }}_h}2x^{2i}A(x)ydx+\frac{1}{2h}{\int }_{{\mathrm{\Gamma }}_h}{x}^{2i}{y}^{3}dx,i=0,1,2.\end{array}$$

(3.1)

Note that the functions $\frac{2x^{2i}A(x)}{A^{\prime }(x)}$ are analytic on $x=1$. Applying Lemma 2.2, we have

$${\int }_{{\mathrm{\Gamma }}_h}2x^{2i}A(x)ydx={\int }_{{\mathrm{\Gamma }}_h}{G}_i(x)y^{3}dx,$$

where $G_i(x)=\frac{1}{9}\frac{(x^4+2i{x}^4-8i{x}^2+3+6i)x^{2i}}{{(x-1)}^2{(x+1)}^2}$. Combined with (3.1), we proved Lemma 3.1. □

Let

$${\tilde{I}}_i(h)={\int }_{{\mathrm{\Gamma }}_h}{f}_i(x)y^{3}dx,$$

then $\{I_0,I_1,I_2\}$ is an ECT-system on $(-\frac{2}{3},0)$ if and only if $\{{\tilde{I}}_0,{\tilde{I}}_1,{\tilde{I}}_2\}$ is as well. Since $s=2$, $n=3$ and the condition $s>n-2$ holds, we can now study if $\{{\tilde{I}}_0,{\tilde{I}}_1,{\tilde{I}}_2\}$ is an ECT-system in the interval $(-\frac{2}{3},0)$ by Lemma 2.1. Thus, set the criteria functions

$$l_i(x)=\left(\frac{f_i}{A^{\prime }}\right)(x)-\left(\frac{f_i}{A^{\prime }}\right)(z(x)),0<x<1,i=0,1,2,$$

where $z(x)$ is the analytic involution $z(x)$ defined by $A(x)=A(z)$. Note that for $0<x<1<z<\sqrt{3}$,

$$A(x)-A(z)=-\frac{1}{6}(x-z)(x+z)(x^2-3+xz+z^2)q(x,z)=0,$$

where

$$q(x,z)=x^2-3-xz+z^2.$$

It is not difficult to find $z(x)$ is implicitly determined by $q(x,z)$, therefore $z^{\prime }(x)=-\frac{2x-z}{-x+2z}$.

In the following, we check if the ordered set of criterion functions $\{l_0(x),l_1(x),l_2(x)\}$ is an ECT-system as $x\in (0,1)$ by verifying the non-vanishing property of continuous Wronskians $W[l_0]$, $W[l_0,l_1]$, $W[l_0,l_1,l_2]$.

Lemma 3.2 The function tuple $\{l_0(x),l_1(x),l_2(x)\}$ is an ECT-system for $x\in (0,1)$.

Proof From Definition 2.1(iii) about continuous Wronskian and with the aid of Maple 13, we have

$$\begin{array}{c}W[l_0(x)]=\frac{2(x-z)p_1(x,z)}{9{(x-1)}^3{(x+1)}^{3}x(x^2-3){(z-1)}^3{(z+1)}^{3}z(z^2-3)},\hfill \\ W[l_0(x),l_1(x)]=\frac{16{(x-z)}^3(x+z)p_2(x,z)}{27x^2{z}^2(x-2z){(z^2-3)}^2{(z+1)}^4{(z-1)}^4{(x^2-3)}^2{(x+1)}^4{(x-1)}^4},\hfill \\ \begin{array}{r}W[l_0(x),l_1(x),l_2(x)]\\ =\frac{256{(x+z)}^3{(x-z)}^6{p}_3(x,z)}{243{(x^2-3)}^3{x}^3{(x+1)}^7{(x-1)}^7{z}^3{(z^2-3)}^3{(z+1)}^7{(z-1)}^7{(x-2z)}^3},\end{array}\hfill \end{array}$$

where $z=z(x)$ is implicitly determined by the equation $q(x,z)=0$ for $0<x<1<z<\sqrt{3}$, while $p_1(x,z)$, $p_2(x,z)$ and $p_3(x,z)$ are polynomials of $(x,z)$ with very long expressions of degree 12, 16 and 28, respectively; their expressions are shown in the Appendix. It is crucial to check if $p_i(x,z)\ne 0$ for all $(x,z)$ satisfies $q(x,z)=0$ and $0<x<1<z<\sqrt{3}$ for $i=1,2,3$ one by one, i.e., to check if $p_i(x,z)=0$ and $q(x,z)=0$ have a common root on $\{(x,z)|0<x<1<z<\sqrt{3}\}$ for $i=0,1,2$.

Firstly, calculating the resultant with respect to z between $q(x,z)$ and $p_1(x,z)$ (i.e., eliminating z from $q(x,z)=0$ and $p_1(x,z)=0$) gives

$$R(q,p_1,z)=4x^2(x^2-3){(x-1)}^6{(x+1)}^6{w}_{1r},$$

where $w_{1r}(x)=25x^8-255x^6+861x^4-1\text{,}107x^2+576$. Applying Sturm’s theorem to $w_{1r}$ gives $w_{1r}(x)\ne 0$ for all $x\in (0,1)$, hence $R(q,p_1,z)\ne 0$ on $(0,1)$. Therefore, $p_1(x,z)=0$ and $q(x,z)=0$ have no common roots, which implies that $W[l_0]\ne 0$ for all $x\in (0,1)$.

Secondly, calculating the resultant with respect to z between $q(x,z)$ and $p_2(x,z)$ gives

$$R(q,p_2,z)=1\text{,}024x^4{(x^2-3)}^2{(x-1)}^8{(x+1)}^8{w}_{2r},$$

where $w_{2r}(x)=900-1\text{,}212x^2+889x^4-260x^6+25x^8$. Applying Sturm’s theorem to $w_{2r}$ gives $w_{2r}(x)\ne 0$ for all $x\in (0,1)$, hence $R(q,p_2,z)\ne 0$ on $(0,1)$. Therefore, $p_2(x,z)=0$ and $q(x,z)=0$ have no common roots, which implies that $W[l_0,l_1]\ne 0$ for all $x\in (0,1)$.

Lastly, calculating the resultant with respect to z between $q(x,z)$ and $p_3(x,z)$ gives

$$R(q,p_3,z)=262\text{,}144x^6{(x^2-3)}^3{(x-1)}^{1}4{(x+1)}^{1}4w_{3r},$$

where $w_{3r}(x)=1\text{,}166\text{,}400-3\text{,}815\text{,}100x^2+5\text{,}589\text{,}000x^4-4\text{,}818\text{,}177x^6+2\text{,}724\text{,}687x^8-987\text{,}504x^{10}+214\text{,}816x^{12}-25\text{,}235x^{14}+1\text{,}225x^{16}$. Applying Sturm’s theorem to $w_{3r}$ gives $w_{3r}(x)\ne 0$ for all $x\in (0,1)$, hence $R(q,p_3,z)\ne 0$ on $(0,1)$. Therefore, $p_3(x,z)=0$ and $q(x,z)=0$ have no common roots, which implies that $W[l_0,l_1,L_2]\ne 0$ for all $x\in (0,1)$.

From the discussion above, three Wronskians do not vanish for $x\in (0,1)$, therefore Lemma 3.2 is proved. □

By Lemma 2.1 and Lemma 3.2, we have proved that $\{{\tilde{I}}_0(h),{\tilde{I}}_1(h),{\tilde{I}}_2(h)\}$ is an ECT-system on $(-\frac{2}{3},0)$, therefore $\{I_0,I_1,I_2\}$ is an ECT-system on $(-\frac{2}{3},0)$ as well. Therefore, $I(h,\delta )$ has at most two zeros on the right half-plane; by symmetry, $I(h,\delta )$ has at most four zeros on the two period annuluses. By the Poincaré-Pontryagin theorem, system (1.6) has at most four limit cycles bifurcated from two annuluses.

4 Conclusion

In this work, we study case 3 for the Liénard system of type $(5,4)$ given above by a new algebra method which is different from the geometrical method used in [17, 18, 20–22]. It is proved that four is the least upper bound of the number of limit cycles bifurcated from two annuluses. Up to now, the least upper bound of the number of limit cycles has been given for six cases of (1.5) except for case 4. By the result of [19], the maximal lower bound of the number of limit cycles for this case is five, therefore the least upper bound is more than or equal to five.

Appendix

As an appendix, we give the expression of the long polynomials $p_1(x,z)$, $p_2(x,z)$ and $p_3(x,z)$.

$$\begin{array}{c}\begin{array}{rl}{p}_1(x,z)=& 5x^8{z}^4+5x^7{z}^5+5x^6{z}^6+5x^5{z}^7+5x^4{z}^8-9x^8{z}^2-9x^7{z}^3-39x^6{z}^4-39x^5{z}^5\\ -39x^4{z}^6-9x^3{z}^7-9x^2{z}^8+6x^8+6x^{7}z+60x^6{z}^2+60x^5{z}^3+120x^4{z}^4\\ +60x^3{z}^5+60x^2{z}^6+6x{z}^7+6z^8-36x^6-36x^{5}z-144x^4{z}^2-94x^3{z}^3\\ -144x^2{z}^4-36x{z}^5-36z^6+72x^4+57x^{3}z+147x^2{z}^2+57x{z}^3+72z^4-60x^2\\ -33xz-60z^2+18,\end{array}\hfill \\ \begin{array}{rl}{p}_2(x,z)=& 10x^{11}{z}^5+15x^{10}{z}^6+30x^9{z}^7+15x^8{z}^8+30x^7{z}^9+15x^6{z}^{10}+10x^5{z}^{11}-16x^{11}{z}^3\\ -24x^{10}{z}^4-148x^9{z}^5-111x^8{z}^6-285x^7{z}^7-111x^6{z}^8-148x^5{z}^9-24x^4{z}^{10}\\ -16x^3{z}^{11}+18x^{11}z+27x^{10}{z}^2+214x^9{z}^3+159x^8{z}^4+834x^7{z}^5+330x^6{z}^6\\ +834x^5{z}^7+159x^4{z}^8+214x^3{z}^9+27x^2{z}^{10}+18x{z}^{11}-180x^{9}z-153x^8{z}^2\\ -1\text{,}065x^7{z}^3-384x^6{z}^4-2\text{,}015x^5{z}^5-384x^4{z}^6-1\text{,}065x^3{z}^7-153x^2{z}^8\\ -180x{z}^9-18x^8+702x^{7}z+255x^6{z}^2+2\text{,}354x^5{z}^3+354x^4{z}^4+2\text{,}354x^3{z}^5\\ +255x^2{z}^6+702x{z}^7-18z^8+111x^6-1\text{,}299x^{5}z-48x^4{z}^2-2\text{,}513x^3{z}^3\\ -48x^2{z}^4-1\text{,}299x{z}^5+111z^6-237x^4+1\text{,}182x^{3}z-252x^2{z}^2+1\text{,}182x{z}^3\\ -237z^4+225x^2-459xz+225z^2-81,\end{array}\hfill \\ \begin{array}{rl}{p}_3(x,z)=& 280x^{17}{z}^{11}-105x^{16}{z}^{12}+840x^{15}{z}^{13}-315x^{14}{z}^{14}+840x^{13}{z}^{15}-105x^{12}{z}^{16}\\ +280x^{11}{z}^{17}-952x^{17}{z}^9+798x^{16}{z}^{10}-7\text{,}042x^{15}{z}^{11}+3\text{,}927x^{14}{z}^{12}\\ -12\text{,}327x^{13}{z}^{13}+3\text{,}927x^{12}{z}^{14}-7\text{,}042x^{11}{z}^{15}+798x^{10}{z}^{16}-952x^9{z}^{17}\\ +1\text{,}848x^{17}{z}^7-1\text{,}953x^{16}{z}^8+20\text{,}104x^{15}{z}^9-16\text{,}905x^{14}{z}^{10}+63\text{,}504x^{13}{z}^{11}\\ -32\text{,}214x^{12}{z}^{12}+63\text{,}504x^{11}{z}^{13}-16\text{,}905x^{10}{z}^{14}+20\text{,}104x^9{z}^{15}-1\text{,}953x^8{z}^{16}\\ +1\text{,}848x^7{z}^{17}-1\text{,}944x^{17}{z}^5+2\text{,}964x^{16}{z}^6-34\text{,}314x^{15}{z}^7+35\text{,}878x^{14}{z}^8\\ -160\text{,}005x^{13}{z}^9+115\text{,}038x^{12}{z}^{10}-268\text{,}979x^{11}{z}^{11}+115\text{,}038x^{10}{z}^{12}\\ -160\text{,}005x^9{z}^{13}+35\text{,}878x^8{z}^{14}-34\text{,}314x^7{z}^{15}+2\text{,}964x^6{z}^{16}-1\text{,}944x^5{z}^{17}\\ +864x^{17}{z}^3-2\text{,}379x^{16}{z}^4+32\text{,}994x^{15}{z}^5-47\text{,}836x^{14}{z}^6+248\text{,}148x^{13}{z}^7\\ -228\text{,}640x^{12}{z}^8+631\text{,}070x^{11}{z}^9-380\text{,}121x^{10}{z}^{10}+631\text{,}070x^9{z}^{11}\\ -228\text{,}640x^8{z}^{12}+248\text{,}148x^7{z}^{13}-47\text{,}836x^6{z}^{14}+32\text{,}994x^5{z}^{15}-2\text{,}379x^4{z}^{16}\\ +864x^3{z}^{17}+630x^{16}{z}^2-13\text{,}992x^{15}{z}^3+34\text{,}590x^{14}{z}^4-221\text{,}895x^{13}{z}^5\\ +284\text{,}359x^{12}{z}^6-919\text{,}212x^{11}{z}^7+732\text{,}354x^{10}{z}^8-1\text{,}425\text{,}248x^9{z}^9\\ +732\text{,}354x^8{z}^{10}-919\text{,}212x^7{z}^{11}+284\text{,}359x^6{z}^{12}-221\text{,}895x^5{z}^{13}\\ +34\text{,}590x^4{z}^{14}-13\text{,}992x^3{z}^{15}+630x^2{z}^{16}+189x^{16}+378x^{15}z-8\text{,}370x^{14}{z}^2\\ +90\text{,}258x^{13}{z}^3-191\text{,}574x^{12}{z}^4+778\text{,}122x^{11}{z}^5-867\text{,}846x^{10}{z}^6\\ +1\text{,}982\text{,}166x^9{z}^7-1\text{,}373\text{,}042x^8{z}^8+1\text{,}982\text{,}166x^7{z}^9-867\text{,}846x^6{z}^{10}\\ +778\text{,}122x^5{z}^{11}-191\text{,}574x^4{z}^{12}+90\text{,}258x^3{z}^{13}-8\text{,}370x^2{z}^{14}+378x{z}^{15}\\ +189z^{16}-2\text{,}349x^{14}-4\text{,}023x^{13}z+41\text{,}598x^{12}{z}^2-305\text{,}397x^{11}{z}^3\\ +547\text{,}713x^{10}{z}^4-1\text{,}599\text{,}747x^9{z}^5+1\text{,}542\text{,}134x^8{z}^6-2\text{,}617\text{,}500x^7{z}^7\\ +1\text{,}542\text{,}134x^6{z}^8-1\text{,}599\text{,}747x^5{z}^9+547\text{,}713x^4{z}^{10}-305\text{,}397x^3{z}^{11}\\ +41\text{,}598x^2{z}^{12}-4\text{,}023x{z}^{13}-2\text{,}349z^{14}+12\text{,}663x^{12}+17\text{,}226x^{11}z\\ -101\text{,}304x^{10}{z}^2+606\text{,}096x^9{z}^3-894\text{,}828x^8{z}^4+2\text{,}004\text{,}954x^7{z}^5\\ -1\text{,}598\text{,}321x^6{z}^6+2\text{,}004\text{,}954x^5{z}^7-894\text{,}828x^4{z}^8+606\text{,}096x^3{z}^9\\ -101\text{,}304x^2{z}^{10}+17\text{,}226x{z}^{11}+12\text{,}663z^{12}-38\text{,}655x^{10}-39\text{,}348x^{9}z\\ +122\text{,}814x^8{z}^2-728\text{,}910x^7{z}^3+809\text{,}760x^6{z}^4-1\text{,}455\text{,}003x^5{z}^5\\ +809\text{,}760x^4{z}^6-728\text{,}910x^3{z}^7+122\text{,}814x^2{z}^8-39\text{,}348x{z}^9-38\text{,}655z^{10}\\ +73\text{,}179x^8+51\text{,}444x^{7}z-39\text{,}519x^6{z}^2+503\text{,}856x^5{z}^3-294\text{,}786x^4{z}^4\\ +503\text{,}856x^3{z}^5-39\text{,}519x^2{z}^6+51\text{,}444x{z}^7+73\text{,}179z^8-88\text{,}659x^6\\ -36\text{,}261x^{5}z-76\text{,}221x^4{z}^2-164\text{,}331x^3{z}^3-76\text{,}221x^2{z}^4-36\text{,}261x{z}^5\\ -88\text{,}659z^6+67\text{,}689x^4+10\text{,}584x^{3}z+90\text{,}477x^2{z}^2+10\text{,}584x{z}^3+67\text{,}689z^4\\ -29\text{,}889x^2-29\text{,}889z^2+5\text{,}832.\end{array}\hfill \end{array}$$