Eisenstein series and their applications to some arithmetic identities and congruences

Abstract

Utilizing the theory of elliptic curves over ℂ to the normalized lattice ${\mathrm{\Lambda }}_{\tau }$, its connection to the Weierstrass ℘-functions and to the Eisenstein series $E_4(\tau )$ and $E_6(\tau )$, we establish some arithmetic identities involving certain arithmetic functions and convolution sums of restricted divisor functions. We also prove some congruence relations involving certain divisor functions and restricted divisor functions.

MSC:11A25, 11A07, 11G99.

1 Introduction

The study of arithmetical identities and congruences is classical in number theory and such investigations have been carried out by several mathematicians including the legend Srinivasa Ramanujan. This study constitutes an important and significant part of the subject number theory.

For $N,m,r,s,d\in \mathbb{Z}$ with $d,s>0$ and $r\ge 0$, we define some divisor functions for our use in the sequel. Let

$${\sigma }_s(N)=\sum _{d|N}{d}^s,$$

and let us define the restricted divisor function

$${\sigma }_{s,r}(N;m)=\underset{d\equiv rmodm}{\sum _{d|N}}{d}^s.$$

Note that

$$\sigma (N):={\sigma }_1(N)=\sum _{d|N}d.$$

For $a,b,n\in \mathbb{N}$, let us define the convolution sum

$$S_{a,b}(n):=\sum _{m=1}^{n-1}{\sigma }_a(m){\sigma }_b(n-m).$$

Ramanujan showed that the sum $S_{a,b}(n)$ can be evaluated in terms of ${\sigma }_{a+b+1}(n),{\sigma }_{a+b-1}(n),\dots ,{\sigma }_3(n),{\sigma }_1(n)$ for the nine pairs $(a,b)\in {\mathbb{N}}^2$ satisfying $a+b=2,4,6,8,12$, $a\le b$, . For example, explicitly, we know (see [1]) that

$$S_{1,11}(n)=\frac{691}{65\text{,}520}{\sigma }_{13}(n)+(\frac{1}{24}-\frac{1}{24}n){\sigma }_{11}(n)-\frac{691}{65\text{,}520}{\sigma }_1(n)$$

(1)

and (see [[2], p.35])

$$S_{3,9}(n)=\frac{1}{2\text{,}640}{\sigma }_{13}(n)-\frac{1}{240}{\sigma }_9(n)+\frac{1}{264}{\sigma }_3(n).$$

(2)

From [3], we note that for any integer $n\ge 3$, we have

$$\begin{array}{c}\underset{m_1+m_2+m_3=n}{\sum _{(m_1,m_2,m_3)\in {\mathbb{N}}^3}}{m}_1{m}_2{\sigma }_1(m_1){\sigma }_1(m_2){\sigma }_1(m_3)\hfill \\ =\frac{1}{288}(n^2{\sigma }_5(n)+(n^2-4n^3){\sigma }_3(n)-(n^3-3n^4){\sigma }_1(n)).\hfill \end{array}$$

(3)

For an elementary proof of (1) and (2), we refer to [4]. An another interesting arithmetical identity (which was stated by Ramanujan, see [[1], p.146], for some analytical proofs of this identity, one may refer to [[5], p.329], [[6], p.136] and [7], also [4]) is for $n\in \mathbb{N}$, we have

$$\sum _{k=0}^{n-1}{\sigma }_1(2k+1){\sigma }_3(n-k)=\frac{1}{240}{\sigma }_5(2n+1)-\frac{1}{240}{\sigma }_3(2n+1).$$

(4)

There are some nice arithmetical identities connecting the divisor functions along with Ramanujan’s τ-function. For instance, we know (see [8]) that

$$\sum _{m=1}^{n-1}m(n-m){\sigma }_3(m){\sigma }_3(n-m)=\frac{1}{540}{n}^2{\sigma }_7(n)-\frac{1}{540}\tau (n)$$

(5)

and from [9], we observe that for $n\in \mathbb{N}\cup \{0\}$,

$$t_{24}(n)=\frac{1}{176\text{,}896}({\sigma }_{11}^{\ast }(n+3)-\tau (n+3)-2\text{,}072\tau \left(\frac{n+3}{2}\right)),$$

(6)

where $t_k(n)$ denotes the number of representations of n as a sum of k triangular numbers, i.e. (with ${\mathbb{N}}_0=\mathbb{N}\cup \{0\}$),

$$\begin{array}{c}{t}_k(n):=\mathrm{\#}\{(m_1,\dots ,m_k)\in {\mathbb{N}}_0^k|n=\frac{1}{2}{m}_1(m_1+1)+\cdots +\frac{1}{2}{m}_k(m_k+1)\},\hfill \\ {\sigma }_k^{\ast }(n):=\underset{\frac{n}{d}\mathrm{odd}}{\sum _{d|n}}{d}^k,\hfill \end{array}$$

and $\tau (n)$ is the coefficient defined by the expression:

$$q{\{(1-q)(1-q^2)\cdots \}}^{24}=\sum _{n=1}^{\mathrm{\infty }}\tau (n)q^n,q\in \mathbb{C}\text{ with }|q|<1.$$

For any integer $k\ge 2$, let

$$r_k(n):=\mathrm{\#}\{(x_1,\dots ,x_k)\in {\mathbb{Z}}^k\mid n=x_1^2+\cdots +x_k^2\}.$$

An another identity worth mentioning (see [1]) is

$$r_{24}(n)=\frac{16}{691}{\sigma }_{11}^{\ast \ast }(n)+\frac{128}{691}(259{(-1)}^{n-1}\tau (n)-512\tau \left(\frac{n}{2}\right)),$$

(7)

where ${\sigma }_k^{\ast \ast }(n):={\sum }_{d|n}{(-1)}^d{d}^k$ and $\tau (\frac{n}{2})=0$ if $\frac{n}{2}$ is not an integer.

From (3), (4) and (5), it is immediate (and interesting) to note that, for $n\in \mathbb{N}$,

(8)

(9)

and

(10)

The proofs of all these identities and congruences heavily depend upon the theory of modular functions and the properties of Eisenstein series. Later some of these identities have been proved using only elementary techniques.

Define the integers $a(n)$ (for $n\in \mathbb{N}$) by

$$\sum _{n=1}^{\mathrm{\infty }}a(n)q^n=q\prod _{n=1}^{\mathrm{\infty }}{(1-q^{2n})}^{12},q\in \mathbb{C}\text{ with }|q|<1.$$

(11)

Also define the integers $b(n)$ (for $n\in \mathbb{N}$) by

$$\sum _{n=1}^{\mathrm{\infty }}b(n)q^n=q\prod _{n=1}^{\mathrm{\infty }}{(1-q^{2n})}^4{(1-q^{4n})}^4,q\in \mathbb{C}\text{ with }|q|<1.$$

(12)

Note that $a(n)\equiv 0$ if and $b(n)\equiv 0$ if . It has been proved by Kenneth Williams (see [10, 11]) that (for $n\in \mathbb{N}$),

$$r_{12}(n)=8{\sigma }_5(n)-512{\sigma }_5\left(\frac{n}{4}\right)+16a(n)$$

(13)

and

$$\begin{array}{rcl}{A}_8(n)& =& \frac{1}{192}{\sigma }_3(n)+\frac{1}{64}{\sigma }_3\left(\frac{n}{2}\right)+\frac{1}{16}{\sigma }_3\left(\frac{n}{4}\right)+\frac{1}{3}{\sigma }_3\left(\frac{n}{8}\right)\\ +(\frac{1}{24}-\frac{1}{32}n){\sigma }_1(n)+(\frac{1}{24}-\frac{1}{4}n){\sigma }_1\left(\frac{n}{8}\right)-\frac{1}{64}b(n),\end{array}$$

where $r_{12}(n)$ is as mentioned before and for $s,n\in \mathbb{N}$,

$$A_s(n):=\underset{k<\frac{n}{s}}{\sum _{k\in \mathbb{N}}}{\sigma }_1(k){\sigma }_1(n-sk).$$

It should be mentioned that Bernoulli identities associated with the Weierstrass ℘-function have been studied by Chang and Srivastava in [12]. Families of Weierstrass type functions and their applications have been investigated by Chang, Srivastava and Wu in [13]. It is also interesting to note that the families of Weierstrass type functions, Weber type functions and their applications have been studied by Aygunes and Simsek in [14]. A few more related references are [15, 16] and [17].

Though there are plenty of identities and congruences involving various arithmetic functions available in the literature, practically nothing seriously known involving restricted divisor functions.

For any integer $M\ge 2$ with $M=p_1^{e_1}\cdots p_r^{e_r}$, we define ${ord}_{p_j}M:=e_j$.

Throughout the paper, $q=e^{2\pi i\tau }$ where $\tau \in \mathfrak{h}=\{x+yi\mid y>0\}$ unless otherwise specified hereafter. The aim of this article is to prove some arithmetical identities involving certain arithmetic functions and convolution sums of restricted divisor functions. We also establish some congruence relations similar to (8), (9) and (10). More precisely, we prove the following theorems.

Theorem 1.1

• (i) For any integer $M\ge 2$, we have

  

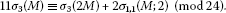
• (ii) Moreover, if M is odd or ${ord}_{p}M$ is odd for an odd prime p, then

  

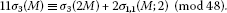
Theorem 1.2 For any integer $M\ge 3$, we have

Theorem 1.3 Let $N\in \mathbb{N}$. Then, we have

$$\begin{array}{c}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}{\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\frac{1}{256}[{\sigma }_5(2N-1)-a(2N-1)],\hfill \end{array}$$

where

$$\sum _{N=1}^{\mathrm{\infty }}a(N)q^N=q\prod _{N=1}^{\mathrm{\infty }}{(1-q^{2N})}^{12}.$$

Corollary 1.4 For $N\in \mathbb{N}$, we have

In particular, if , then we have

Theorem 1.5 Let $N\in \mathbb{N}$. Then we have

$$\begin{array}{c}\sum _{M=1}^{N-1}\sum _{m=1}^{M-1}{\sigma }_{1,1}(2N-1-2M;2){\sigma }_{1,1}(M-m;2){\sigma }_{1,1}(m;2)\hfill \\ =\frac{1}{2\text{,}304}[{\sigma }_5(2N-1)-8{\sigma }_3(2N-1)+4{\sigma }_1(2N-1)+3a(2N-1)].\hfill \end{array}$$

Remark The main idea in proving Theorems 1.1 and 1.2 is to obtain q-series expansions for $E_4(\tau )$ and $E_6(\tau )$ with coefficients being restricted divisor functions and their convolution sums. Then we have to compare these expressions with the already known q-series expressions of $E_4(\tau )$ and $E_6(\tau )$.

The paper is organized as follows. In Section 2, we express $g_2(\tau )$ and $g_3(\tau )$ in terms of q-products. In Section 3, $g_2(\tau )$ and $g_3(\tau )$ are transformed into expressions involving $S_1$ and $S_2$ where $S_1$ and $S_2$ are q-series expressions with coefficients as restricted divisor functions. Then we obtain q-series expressions for $E_4(\tau )$ and $E_6(\tau )$ with coefficients being restricted divisor functions and their convolution sums. Then we compare these expressions of $E_4(\tau )$ and $E_6(\tau )$ with already known expressions. Section 4 concludes the proofs of Theorems 1.1 and 1.2. In proving arithmetical identities involving the coefficient $a(n)$ (where $a(n)$ is defined as in (11)), we need to study the quantities $S_1^3$ and $S_1{S}_2^2$ and in turn the convolution sums of restricted divisor functions along with $a(n)$ come out very naturally.

2 q-product expressions for the Eisenstein series $g_2(\tau )$and $g_3(\tau )$

Let ${\mathrm{\Lambda }}_{\tau }=\mathbb{Z}+\tau \mathbb{Z}$ ($\tau \in \mathfrak{H}$ the complex upper half plane) be a lattice and $z\in \mathbb{C}$. The Weierstrass ℘ function relative to ${\mathrm{\Lambda }}_{\tau }$ is defined by the series

$$\mathrm{\wp }(z;{\mathrm{\Lambda }}_{\tau })=\frac{1}{z^2}+\underset{\omega \ne 0}{\sum _{\omega \in {\mathrm{\Lambda }}_{\tau }}}\{\frac{1}{{(z-\omega )}^2}-\frac{1}{{\omega }^2}\},$$

and the Eisenstein series of weight 2k for ${\mathrm{\Lambda }}_{\tau }$ with $k>1$ is the series

$$G_{2k}({\mathrm{\Lambda }}_{\tau })=\underset{\omega \ne 0}{\sum _{\omega \in {\mathrm{\Lambda }}_{\tau }}}{\omega }^{-2k}.$$

We shall use the notations $\mathrm{\wp }(z)$ and $G_{2k}$ instead of $\mathrm{\wp }(z;{\mathrm{\Lambda }}_{\tau })$ and $G_{2k}({\mathrm{\Lambda }}_{\tau })$, respectively, when the lattice ${\mathrm{\Lambda }}_{\tau }$ has been fixed. Then the Laurent series for $\mathrm{\wp }(z)$ about $z=0$ is given by

$$\mathrm{\wp }(z)=z^{-2}+\sum _{k=1}^{\mathrm{\infty }}(2k+1)G_{2k+2}{z}^{2k}.$$

As is customary, by setting

$$g_2(\tau )=g_2({\mathrm{\Lambda }}_{\tau })=60G_4\text{and}{g}_3(\tau )=g_3({\mathrm{\Lambda }}_{\tau })=140G_6,$$

the algebraic relation between $\mathrm{\wp }(z)$ and ${\mathrm{\wp }}^{\mathrm{\prime }}(z)$ becomes

$${\mathrm{\wp }}^{\mathrm{\prime }}{(z)}^2=4\mathrm{\wp }{(z)}^3-g_2(\tau )\mathrm{\wp }(z)-g_3(\tau ).$$

We use the following q-product expressions:

$$\begin{array}{c}{P}_0=\prod _{n=1}^{\mathrm{\infty }}(1-q^{2n}),P_1=\prod _{n=1}^{\mathrm{\infty }}(1-q^{2n-1}),\hfill \\ P_2=\prod _{n=1}^{\mathrm{\infty }}(1+q^{2n}),P_3=\prod _{n=1}^{\mathrm{\infty }}(1+q^{2n-1}).\hfill \end{array}$$

Theorem 2.1 We have

$$g_2(\tau )=\frac{4{\pi }^4}{3}{P}_0^8(P_3^{16}-2^{4}q{P}_2^8{P}_3^8+2^8{q}^2{P}_2^{16})$$

and

$$g_3(\tau )=\frac{4{\pi }^6}{27}{P}_0^{12}(-2P_3^{24}+3P_1^8{P}_3^{16}+3P_1^{16}{P}_3^8-2P_1^{24}).$$

To prove Theorem 2.1, we need the following lemma.

Lemma 2.2 Let $e_1=\mathrm{\wp }(\frac{\tau }{2})$, $e_2=\mathrm{\wp }(\frac{1}{2})$ and $e_3=\mathrm{\wp }(\frac{\tau +1}{2})$.

• (1) $e_2-e_1={\pi }^2{P}_0^4{P}_3^8$.

• (2) $e_2-e_3={\pi }^2{P}_0^4{P}_1^8$.

• (3) $e_3-e_1=2^4{\pi }^{2}q{P}_0^4{P}_2^8$.

Proof See [18]. □

Proof of Theorem 2.1 From [[19], p.63], we observe that $e_1$, $e_2$ and $e_3$ are the roots of the equation

$$4\mathrm{\wp }{(z)}^3-g_2(\tau )\mathrm{\wp }(z)-g_3(\tau )=0.$$

Therefore, we have

$$\begin{array}{c}{e}_1+e_2+e_3=0,\hfill \\ e_1{e}_2+e_2{e}_3+e_3{e}_1=-\frac{g_2(\tau )}{4}\hfill \end{array}$$

and

$$e_1{e}_2{e}_3=\frac{g_3(\tau )}{4}.$$

By the above equations and Lemma 2.2, we deduce that

$$2e_1+e_3=e_1-(-e_3-e_1)=e_1-e_2=-{\pi }^2{P}_0^4{P}_3^8,$$

and the following three identities:

$$\begin{array}{rl}{e}_1& =\frac{1}{3}[(2e_1+e_3)+(e_1-e_3)]\\ =\frac{1}{3}(-{\pi }^2{P}_0^4{P}_3^8-2^4{\pi }^{2}q{P}_0^4{P}_2^8)\\ =-\frac{{\pi }^2}{3}{P}_0^4(P_3^8+2^{4}q{P}_2^8),\end{array}$$

(14)

$$e_3=e_1+2^4{\pi }^{2}q{P}_0^4{P}_2^8=-\frac{{\pi }^2}{3}{P}_0^4(P_3^8-2^{5}q{P}_2^8)$$

(15)

and

$$e_2=e_1+{\pi }^2{P}_0^4{P}_3^8=-\frac{{\pi }^2}{3}{P}_0^4(-2P_3^8+2^{4}q{P}_2^8).$$

(16)

Using (14), (15) and (16), we obtain the identities for $g_2(\tau )$ and $g_3(\tau )$, namely

$$\begin{array}{rcl}{g}_2(\tau )& =& -4(e_1{e}_2+e_2{e}_3+e_3{e}_1)\\ =& -\frac{4{\pi }^4}{9}{P}_0^8[(P_3^8+2^{4}q{P}_2^8)(-2P_3^8+2^{4}q{P}_2^8)\\ +(P_3^8-2^{5}q{P}_2^8)(-2P_3^8+2^{4}q{P}_2^8)\\ +(P_3^8+2^{4}q{P}_2^8)(P_3^8-2^{5}q{P}_2^8)]\\ =& \frac{4{\pi }^4}{3}{P}_0^8(P_3^{16}-2^{4}q{P}_2^8{P}_3^8+2^8{q}^2{P}_2^{16})\end{array}$$

(17)

and

$$\begin{array}{rcl}{g}_3(\tau )& =& 4e_1{e}_2{e}_3\\ =& -\frac{4{\pi }^6}{27}{P}_0^{12}(P_3^8+2^{4}q{P}_2^8)(-2P_3^8+2^{4}q{P}_2^8)(P_3^8-2^{5}q{P}_2^8)\\ =& \frac{4{\pi }^6}{27}{P}_0^{12}(-2P_3^{24}+3P_1^8{P}_3^{16}+3P_1^{16}{P}_3^8-2P_1^{24}).\end{array}$$

(18)

This proves the theorem. □

3 Eisenstein series and divisor functions

We use the q-series and q-products notions

$$\begin{array}{c}{S}_1:=\sum _{N\mathrm{odd}}{\sigma }_{1,1}(N;2)q^N,\hfill \\ S_2:=\sum _{N\ge 2\mathrm{even}}{\sigma }_{1,1}(N;2)q^N,\hfill \\ {(a;q)}_{\mathrm{\infty }}:={(a)}_{\mathrm{\infty }}:=\prod _{n\ge 0}(1-a{q}^n)\hfill \end{array}$$

in the following. Some identities of the basic hypergeometric series type are quoted by Fine (see [20]). Some of these identities (in a similar form) can also be found in [21] and [22]. It should be mentioned that some generalizations and basic q-extensions of Bernoulli, Euler and Genocchi polynomials have been studied recently by Srivastava (see [23]). We also refer to [24] in which zeta and q-zeta function, associated series and integrals have been investigated by Srivastava and Choi. We mention below two identities (see [[20], p.78, p.79]) for our further use. These are

$$\frac{{(q^2;q^2)}_{\mathrm{\infty }}^{20}}{{(q)}_{\mathrm{\infty }}^8{(q^4;q^4)}_{\mathrm{\infty }}^8}=1+8\sum _{N=1}^{\mathrm{\infty }}{q}^N(2+{(-1)}^N)\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega$$

(19)

and

$$\frac{q{(q^4;q^4)}_{\mathrm{\infty }}^8}{{(q^2;q^2)}_{\mathrm{\infty }}^4}=\sum _{N\mathrm{odd}}\sigma (N)q^N.$$

(20)

Using (19), (20) and the facts,

$$\prod _{n=1}^{\mathrm{\infty }}(1-q^{2n-1})=\prod _{n=1}^{\mathrm{\infty }}\frac{(1-q^n)}{(1-q^{2n})},\prod _{n=1}^{\mathrm{\infty }}(1+q^{2n-1})=\prod _{n=1}^{\mathrm{\infty }}\frac{(1-q^{2n})}{(1-q^n)}\frac{(1-q^{2n})}{(1-q^{4n})}$$

and

$$\prod _{n=1}^{\mathrm{\infty }}(1+q^{2n})=\prod _{n=1}^{\mathrm{\infty }}\frac{(1-q^{4n})}{(1-q^{2n})},$$

our aim here is first to prove the following lemma.

Lemma 3.1 Let $q=e^{2\pi i\tau }$, $\tau \in \mathfrak{H}$. Then we have

• (a)
  $$\mathrm{\wp }\left(\frac{\tau }{2}\right)=-\frac{{\pi }^2}{3}(1+24S_1+24S_2).$$
• (b)
  $$\mathrm{\wp }\left(\frac{\tau +1}{2}\right)=-\frac{{\pi }^2}{3}(1-24S_1+24S_2).$$
• (c)
  $$\mathrm{\wp }\left(\frac{1}{2}\right)=\frac{2{\pi }^2}{3}(1+24S_2).$$

Proof

• (a) From (14), we have

  $$\begin{array}{rcl}\mathrm{\wp }\left(\frac{\tau }{2}\right)& =& -\frac{{\pi }^2}{3}(\frac{{(q^2;q^2)}_{\mathrm{\infty }}^{20}}{{(q)}_{\mathrm{\infty }}^8{(q^4;q^4)}_{\mathrm{\infty }}^8}+16\frac{q{(q^4;q^4)}_{\mathrm{\infty }}^8}{{(q^2;q^2)}_{\mathrm{\infty }}^4})\\ =& -\frac{{\pi }^2}{3}(1+8\sum _{N=1}^{\mathrm{\infty }}{q}^N(2+{(-1)}^N)\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega +16\sum _{N\mathrm{odd}}\sigma (N)q^N)\\ =& -\frac{{\pi }^2}{3}(1+8\sum _{N\mathrm{odd}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega +24\sum _{N\mathrm{even}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega +16\sum _{N\mathrm{odd}}\sigma (N)q^N)\\ =& -\frac{{\pi }^2}{3}(1+24\sum _{N=1}^{\mathrm{\infty }}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega )\\ =& -\frac{{\pi }^2}{3}(1+24\sum _{N=1}^{\mathrm{\infty }}{\sigma }_{1,1}(N;2)q^N)\\ =& -\frac{{\pi }^2}{3}(1+24S_1+24S_2).\end{array}$$

  (21)

• (b) From (15), we have

  $$\begin{array}{c}\mathrm{\wp }\left(\frac{\tau +1}{2}\right)\hfill \\ =-\frac{{\pi }^2}{3}(\frac{{(q^2;q^2)}_{\mathrm{\infty }}^{20}}{{(q)}_{\mathrm{\infty }}^8{(q^4;q^4)}_{\mathrm{\infty }}^8}-32\frac{q{(q^4;q^4)}_{\mathrm{\infty }}^8}{{(q^2;q^2)}_{\mathrm{\infty }}^4})\hfill \\ =-\frac{{\pi }^2}{3}(1+8\sum _{N=1}^{\mathrm{\infty }}{q}^N(2+{(-1)}^N)\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega -32\sum _{N\mathrm{odd}}\sigma (N)q^N)\hfill \\ =-\frac{{\pi }^2}{3}(1+8\sum _{N\mathrm{odd}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega +24\sum _{N\mathrm{even}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega -32\sum _{N\mathrm{odd}}\sigma (N)q^N)\hfill \\ =-\frac{{\pi }^2}{3}(1+24\sum _{N=1}^{\mathrm{\infty }}{(-1)}^N{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega )\hfill \\ =-\frac{{\pi }^2}{3}(1+24\sum _{N=1}^{\mathrm{\infty }}{(-1)}^N{\sigma }_{1,1}(N;2)q^N)\hfill \\ =-\frac{{\pi }^2}{3}(1-24S_1+24S_2).\hfill \end{array}$$

  (22)

• (c) From (16), we have

  $$\begin{array}{rcl}\mathrm{\wp }\left(\frac{1}{2}\right)& =& \frac{2{\pi }^2}{3}(\frac{{(q^2;q^2)}_{\mathrm{\infty }}^{20}}{{(q)}_{\mathrm{\infty }}^8{(q^4;q^4)}_{\mathrm{\infty }}^8}-8\frac{q{(q^4;q^4)}_{\mathrm{\infty }}^8}{{(q^2;q^2)}_{\mathrm{\infty }}^4})\\ =& \frac{2{\pi }^2}{3}(1+8\sum _{N=1}^{\mathrm{\infty }}{q}^N(2+{(-1)}^N)\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega -8\sum _{N\mathrm{odd}}\sigma (N)q^N)\\ =& \frac{2{\pi }^2}{3}(1+8\sum _{N\mathrm{odd}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega +24\sum _{N\mathrm{even}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega -8\sum _{N\mathrm{odd}}\sigma (N)q^N)\\ =& \frac{2{\pi }^2}{3}(1+24\sum _{N\mathrm{even}}{q}^N\underset{\omega \mathrm{odd}}{\sum _{\omega |N}}\omega )\\ =& \frac{2{\pi }^2}{3}(1+24\sum _{N\mathrm{even}}{\sigma }_{1,1}(N;2)q^N)\\ =& \frac{2{\pi }^2}{3}(1+24S_2).\end{array}$$

  (23)

This proves the lemma. □

Using the fact that $e_1$, $e_2$ and $e_3$ are the roots of the equation $4\mathrm{\wp }{(z)}^3-g_2(\tau )\mathrm{\wp }(z)-g_3(\tau )=0$, indeed we can express $g_2(\tau )$ and $g_3(\tau )$ in terms of $S_1$ and $S_2$. More precisely, we have the following lemma.

Lemma 3.2 We have

$$g_2(\tau )=\frac{4{\pi }^4}{9}[3{(1+24S_2)}^2+{24}^2{S}_1^2]$$

and

$$g_3(\tau )=\frac{8{\pi }^6}{27}[{(1+24S_2)}^3-{24}^2{S}_1^2(1+24S_2)].$$

Proof Note that $g_2(\tau )=-4[e_1{e}_2+e_2{e}_3+e_3{e}_1]$, and hence

$$\begin{array}{rcl}{g}_2(\tau )& =& -4[\mathrm{\wp }\left(\frac{\tau }{2}\right)\mathrm{\wp }\left(\frac{1}{2}\right)+\mathrm{\wp }\left(\frac{1}{2}\right)\mathrm{\wp }\left(\frac{\tau +1}{2}\right)+\mathrm{\wp }\left(\frac{\tau +1}{2}\right)\mathrm{\wp }\left(\frac{\tau }{2}\right)]\\ =& -4[-\frac{2{\pi }^4}{9}(1+24S_1+24S_2)(1+24S_2)-\frac{2{\pi }^4}{9}(1+24S_2)(1-24S_1+24S_2)\\ +\frac{{\pi }^4}{9}(1-24S_1+24S_2)(1+24S_1+24S_2)]\\ =& \frac{4{\pi }^4}{9}[3{(1+24S_2)}^2+{24}^2{S}_1^2].\end{array}$$

Also note that $g_3(\tau )=4e_1{e}_2{e}_3$, and hence

$$\begin{array}{rcl}{g}_3(\tau )& =& 4\mathrm{\wp }\left(\frac{\tau }{2}\right)\mathrm{\wp }\left(\frac{1}{2}\right)\mathrm{\wp }\left(\frac{\tau +1}{2}\right)\\ =& \frac{8{\pi }^6}{27}(1+24S_1+24S_2)(1+24S_2)(1-24S_1+24S_2)\\ =& \frac{8{\pi }^6}{27}[{(1+24S_2)}^3-{24}^2{S}_1^2(1+24S_2)].\end{array}$$

This completes the proof of the lemma. □

In the next theorem, we give q-series expressions for $E_4(\tau )$ and $E_6(\tau )$ with the coefficients involving restricted divisor functions ${\sigma }_{1,1}(N;2)$ and its convolution sums. Precisely, we prove the following theorem.

Theorem 3.3 We have

$$\begin{array}{rcl}{E}_4(\tau )& =& \frac{2^2\cdot 3}{{(2\pi )}^4}{g}_2(\tau )\\ =& 1+240q+\sum _{M=2}^{\mathrm{\infty }}[48{\sigma }_{1,1}(2M;2)+576\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +192\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)]q^M\end{array}$$

and

$$\begin{array}{rcl}{E}_6(\tau )& =& \frac{2^3\cdot 3^3}{{(2\pi )}^6}{g}_3(\tau )\\ =& 1-504q-16\text{,}632q^2+\sum _{M=3}^{\mathrm{\infty }}[72{\sigma }_{1,1}(2M;2)+1\text{,}728\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +13\text{,}824\underset{k+l+m=M}{\overset{M-2}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)\\ -576\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)\\ -13\text{,}824\underset{k+l+m-1=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)]q^M.\end{array}$$

Proof

From Lemma 3.2, we observe that

$$\begin{array}{rcl}{E}_4(\tau )& =& \frac{2^2\cdot 3}{{(2\pi )}^4}{g}_2(\tau )\\ =& \frac{2^2\cdot 3}{{(2\pi )}^4}\cdot \frac{4{\pi }^4}{9}[3{(1+24S_2)}^2+{24}^2{S}_1^2]\\ =& 1+48S_2+576S_2^2+192S_1^2\\ =& 1+48\sum _{M=1}^{\mathrm{\infty }}{\sigma }_{1,1}(2M;2)q^{2M}\\ +576\underset{k+l=M}{\overset{\mathrm{\infty }}{\sum _{M=2}}}\sum _{k=1}^{M-1}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)q^{2M}\\ +192\underset{k+l-1=M}{\overset{\mathrm{\infty }}{\sum _{M=1}}}\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)q^{2M}\\ =& 1+48{\sigma }_{1,1}(2;2)q^2+48\sum _{M=2}^{\mathrm{\infty }}{\sigma }_{1,1}(2M;2)q^{2M}\\ +576\sum _{M=2}^{\mathrm{\infty }}\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)q^{2M}\\ +192{\sigma }_{1,1}(1;2){\sigma }_{1,1}(1;2)q^2+192\underset{k+l-1=M}{\overset{\mathrm{\infty }}{\sum _{M=2}}}\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)q^{2M}\\ =& 1+240q^2+\sum _{M=2}^{\mathrm{\infty }}[48{\sigma }_{1,1}(2M;2)+576\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +192\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)]q^{2M}\end{array}$$

and

$$\begin{array}{rcl}{E}_6(\tau )& =& \frac{2^3\cdot 3^3}{{(2\pi )}^6}{g}_3(\tau )\\ =& 1+72S_2+1\text{,}728S_2^2+13\text{,}824S_2^3-576S_1^2-13\text{,}824S_1^2{S}_2\\ =& 1+72\sum _{M=1}^{\mathrm{\infty }}{\sigma }_{1,1}(2M;2)q^{2M}+1\text{,}728\underset{k+l=M}{\overset{\mathrm{\infty }}{\sum _{M=2}}}\sum _{k=1}^{M-1}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)q^{2M}\\ +13\text{,}824\underset{k+l+m=M}{\overset{\mathrm{\infty }}{\sum _{M=3}}}\sum _{k=1}^{M-2}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)q^{2M}\\ -576\underset{k+l-1=M}{\overset{\mathrm{\infty }}{\sum _{M=1}}}\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)q^{2M}\\ -13\text{,}824\underset{k+l+m-1=M}{\overset{\mathrm{\infty }}{\sum _{M=2}}}\sum _{k=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)q^{2M}\\ =& 1+72{\sigma }_{1,1}(2;2)q^2+72{\sigma }_{1,1}(4;2)q^4+72\sum _{M=3}^{\mathrm{\infty }}{\sigma }_{1,1}(2M;2)q^{2M}\\ +1\text{,}728{\sigma }_{1,1}(2;2){\sigma }_{1,1}(2;2)q^4+1\text{,}728\sum _{M=3}^{\mathrm{\infty }}\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)q^{2M}\\ +13\text{,}824\sum _{M=3}^{\mathrm{\infty }}\underset{k+l+m=M}{\overset{M-2}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)q^{2M}\\ -576{\sigma }_{1,1}(1;2){\sigma }_{1,1}(1;2)q^2-576[{\sigma }_{1,1}(1;2){\sigma }_{1,1}(3;2)+{\sigma }_{1,1}(3;2){\sigma }_{1,1}(1;2)]\\ -576\sum _{M=3}^{\mathrm{\infty }}\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)q^{2M}\\ -13\text{,}824{\sigma }_{1,1}(1;2){\sigma }_{1,1}(1;2){\sigma }_{1,1}(2;2)q^4\\ -13\text{,}824\sum _{M=3}^{\mathrm{\infty }}\underset{k+l+m-1=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)q^{2M}\\ =& 1+72q^2+72q^4+1\text{,}728q^4-576q^2-4\text{,}608q^4-13\text{,}824q^4\\ +\sum _{M=3}^{\mathrm{\infty }}[72{\sigma }_{1,1}(2M;2)+1\text{,}728\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +13\text{,}824\underset{k+l+m=M}{\overset{M-2}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)\\ -576\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)\\ -13\text{,}824\underset{k+l+m-1=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)]q^{2M}.\end{array}$$

Now replacing $q^2$ into q in the above expressions for $E_4(\tau )$ and $E_6(\tau )$, we obtain

$$\begin{array}{rcl}{E}_4(\tau )& =& 1+240q+\sum _{M=2}^{\mathrm{\infty }}[48{\sigma }_{1,1}(2M;2)+576\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +192\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)]q^M\end{array}$$

(24)

and

$$\begin{array}{rcl}{E}_6(\tau )& =& 1-504q-16\text{,}632q^2+\sum _{M=3}^{\mathrm{\infty }}[72{\sigma }_{1,1}(2M;2)+1\text{,}728\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +13\text{,}824\underset{k+l+m=M}{\overset{M-2}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)\\ -576\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)\\ -13\text{,}824\underset{k+l+m-1=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)]q^M.\end{array}$$

(25)

This completes the proof of the theorem. □

It should be noted that $E_4(\tau )$ and $E_6(\tau )$ themselves have coefficients ${\sigma }_3(M)$ and ${\sigma }_5(M)$ in their q-series expansions. However, the aim of the next theorem is to express ${\sigma }_3(M)$ and ${\sigma }_5(M)$ in terms of convolution sums involving restricted divisor functions ${\sigma }_{1,1}(N;2)$.

Theorem 3.4 (a) If $M\ge 2$ is an integer, then

$$\begin{array}{rcl}5{\sigma }_3(M)& =& {\sigma }_{1,1}(M;2)+12\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +4\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2M-2k+1;2).\end{array}$$

In particular, if $M\ge 3$ is odd, then

$$\sum _{k=1}^{\frac{M-1}{2}}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)=\frac{1}{24}[{\sigma }_3(M)-{\sigma }_{1,1}(M;2)].$$

• (b) If $M\ge 3$ is an integer, then

  $$\begin{array}{rcl}-7{\sigma }_5(M)& =& {\sigma }_{1,1}(M;2)+24\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +192\sum _{k,l=1}^{M-2}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(l;2){\sigma }_{1,1}(M-k-l;2)\\ -8\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2M-2k+1;2)\\ -192\sum _{k,l=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(M-k-l+1;2).\end{array}$$

In particular, if $M\ge 3$ is odd, then

$$\begin{array}{rcl}-7{\sigma }_5(M)+8{\sigma }_3(M)& =& {\sigma }_{1,1}(M;2)+24\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +192\sum _{k,l=1}^{M-2}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(l;2){\sigma }_{1,1}(M-k-l;2)\\ -192\sum _{k,l=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(M-k-l+1;2).\end{array}$$

Proof From [[19], p.59], we know that

$$E_4(\tau )=1+240\sum _{M\ge 1}{\sigma }_3(M)q^M$$

(26)

and

$$E_6(\tau )=1-504\sum _{M\ge 1}{\sigma }_5(M)q^M.$$

(27)

So comparing (24) and (26), we find that

$$\begin{array}{rcl}5{\sigma }_3(M)& =& {\sigma }_{1,1}(2M;2)+12\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +4\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)\\ =& {\sigma }_{1,1}(M;2)+12\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +4\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2M-2k+1;2),\end{array}$$

(28)

where $M\ge 2$.

On the other hand, Liouville [25] proved

$${\sigma }_3(M)=\sum _{k=1}^M\sigma (2k-1)\sigma (2M-2k+1)$$

(29)

for odd M. From (28) and (29), we note that we reprove a result in [[26], p.300], namely,

$$5{\sigma }_3(M)={\sigma }_{1,1}(M;2)+12\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)+4{\sigma }_3(M)$$

and so,

$$\begin{array}{rcl}{\sigma }_3(M)& =& {\sigma }_{1,1}(M;2)+12\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ =& \sigma (M)+24\sum _{k=1}^{\frac{M-1}{2}}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\end{array}$$

(30)

for odd M. By the same way, comparing (25) and (27), we deduce

$$\begin{array}{rcl}-7{\sigma }_5(M)& =& {\sigma }_{1,1}(2M;2)+24\underset{k+l=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2)\\ +192\underset{k+l+m=M}{\overset{M-2}{\sum _{k=1}}}{\sigma }_{1,1}(2k;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)\\ -8\underset{k+l-1=M}{\overset{M}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2)\\ -192\underset{k+l+m-1=M}{\overset{M-1}{\sum _{k=1}}}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m;2)\\ =& {\sigma }_{1,1}(M;2)+24\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +192\sum _{k,l=1}^{M-2}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(l;2){\sigma }_{1,1}(M-k-l;2)\\ -8\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2M-2k+1;2)\\ -192\sum _{k,l=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(M-k-l+1;2),\end{array}$$

(31)

where $M\ge 3$. Note that for odd $M\ge 3$, we get

$$\begin{array}{rcl}-7{\sigma }_5(M)& =& {\sigma }_{1,1}(M;2)+24\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)\\ +192\sum _{k,l=1}^{M-2}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(l;2){\sigma }_{1,1}(M-k-l;2)-8{\sigma }_3(M)\\ -192\sum _{k,l=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(M-k-l+1;2),\end{array}$$

(32)

where we used Equation (29). This completes the proof of the theorem. □

4 Proof of the theorems

Proof of Theorem 1.1 Glaisher proved that (see [[26], p.300])

$$\sigma (1)\sigma (2n-1)+\sigma (3)\sigma (2n-3)+\cdots +\sigma (2n-1)\sigma (1)=\frac{1}{8}[{\sigma }_3(2n)-{\sigma }_3(n)].$$

(33)

It follows directly from (28) that

$$\begin{array}{c}\sigma (1)\sigma (2M-1)+\sigma (3)\sigma (2M-3)+\cdots +\sigma (2M-1)\sigma (1)\hfill \\ =\sum _{k=1}^M{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2M-2k+1;2)\hfill \end{array}$$

and

$$5{\sigma }_3(M)={\sigma }_{1,1}(M;2)+12\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)+\frac{1}{2}[{\sigma }_3(2M)-{\sigma }_3(M)].$$

Thus, we have proved the identity

$$\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)=\frac{1}{24}[11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)].$$

(34)

Thus, for any integer $M\ge 2$, we have

This proves (i).

We note that we can write (34) as

$$\begin{array}{c}2\sum _{k<\frac{M}{2}}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)+{\sigma }_{1,1}(\frac{M}{2};2){\sigma }_{1,1}(\frac{M}{2};2)\hfill \\ =\frac{1}{24}[11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)].\hfill \end{array}$$

(35)

If M is odd, then (35) is equivalent to

$$24\cdot 2\sum _{k<\frac{M}{2}}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)=11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)$$

and hence,

Let $M=2^m{p}^n{p}_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r}$. Therefore, if ${ord}_{p}M=n$ is odd for an odd prime p, then we note that

$$\begin{array}{rcl}{\sigma }_{1,1}(\frac{M}{2};2){\sigma }_{1,1}(\frac{M}{2};2)& =& {\sigma }_{1,1}(2^{m-1}{p}^n{p}_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r};2){\sigma }_{1,1}(2^{m-1}{p}^n{p}_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r};2)\\ =& {\left\{{\sigma }_{1,1}(2^{m-1};2)\right\}}^2{\left\{{\sigma }_1(p^n{p}_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r})\right\}}^2\\ =& {\left\{{\sigma }_1\left(p^n\right)\right\}}^2{\left\{{\sigma }_{1,1}(2^{m-1};2)\right\}}^2{\left\{{\sigma }_1(p_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r})\right\}}^2\\ =& {(2l)}^2{\left\{{\sigma }_{1,1}(2^{m-1};2)\right\}}^2{\left\{{\sigma }_1(p_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r})\right\}}^2,\end{array}$$

since

and so we can write ${\sigma }_1(p^n)=2l$ for some $l\in \mathbb{N}$. Therefore, from (35), we obtain

$$\begin{array}{c}2\sum _{k<\frac{M}{2}}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)+2\cdot 2l^2{\left\{{\sigma }_{1,1}(2^{m-1};2)\right\}}^2{\left\{{\sigma }_1(p_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r})\right\}}^2\hfill \\ =\frac{1}{24}[11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)].\hfill \end{array}$$

This means that

This proves (ii). □

Remark 4.1

Define

$$P(N):=\{p:p|N,p\text{ is a positive prime}\}$$

and

$$P_{max}(N):=\underset{p\in P(N)}{max}p.$$

For example, $P(10)=\{2,5\}$ and $P_{max}(10)=5$. For any prime $p\ge 5$, we note that

$$P_{max}(\sum _{k=1}^{p-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(p-k;2))=p.$$

We observe that

$$\sum _{k=1}^{p-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(p-k;2)=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{p+1}{3}\right)=\frac{(p+1)p(p-1)}{12}$$

and $(p,12)=1$. Thus, $12|(p^2-1)$ and this implies that the largest prime factor of $p^2-1$ is strictly <p.

Remark 4.2

From the fact

$${\sigma }_{1,1}(k;2)={\sigma }_1(k)-2{\sigma }_1\left(\frac{k}{2}\right),$$

and from known results, it is possible to establish the following identity (in an elementary way, without using the Eisenstein series), namely

$$\sum _{k=1}^{M-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(M-k;2)=\frac{1}{12}{\sigma }_3(M)+\frac{1}{3}{\sigma }_3\left(\frac{M}{2}\right)-\frac{1}{12}{\sigma }_1(M)+\frac{1}{6}{\sigma }_1\left(\frac{M}{2}\right).$$

One can also use this identity to obtain

$$\sum _{k=1}^{p-1}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(p-k;2)=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{p+1}{3}\right).$$

Proof of Theorem 1.2 Inserting (33) and (34) into (31), we obtain

$$\begin{array}{rcl}-7{\sigma }_5(M)& =& {\sigma }_{1,1}(M;2)+24\cdot \frac{1}{24}[11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)]\\ +192\sum _{k,l=1}^{M-2}{\sigma }_{1,1}(k;2){\sigma }_{1,1}(l;2){\sigma }_{1,1}(M-k-l;2)-8\cdot \frac{1}{8}[{\sigma }_3(2M)-{\sigma }_3(M)]\\ -192\sum _{k,l=1}^{M-1}{\sigma }_{1,1}(2k-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(M-k-l+1;2).\end{array}$$

Thus, we deduce the congruence relation

This completes the proof of Theorem 1.2. □

Proof of Theorem 1.3 We expand $S_1^3$ as

$$\begin{array}{c}\sum _{n,l,m=1}^{\mathrm{\infty }}{\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)q^{2(n+l+m-1)-1}\hfill \\ =\sum _{N=2}^{\mathrm{\infty }}\{\sum _{M=1}^{N-1}\sum _{m=1}^M{\sigma }_{1,1}(2N-1-2M;2)\hfill \\ \times {\sigma }_{1,1}(2M-(2m-1);2){\sigma }_{1,1}(2m-1;2)\}{q}^{2N-1}.\hfill \end{array}$$

Then we notice that

$$\begin{array}{c}\sum _{M=1}^{N-1}\sum _{m=1}^M{\sigma }_{1,1}(2N-1-2M;2){\sigma }_{1,1}(2M-(2m-1);2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\sum _{M=1}^{N-1}{\sigma }_{1,1}(2N-1-2M;2)\{\sum _{m=1}^M{\sigma }_{1,1}(2M-(2m-1);2){\sigma }_{1,1}(2m-1;2)\}\hfill \\ =\sum _{M=1}^{N-1}{\sigma }_1(2N-1-2M)\cdot \frac{1}{8}({\sigma }_3(2M)-{\sigma }_3(M))\hfill \end{array}$$

(36)

by [[27], Lemma 3.1(b)] and ${\sigma }_{1,1}(\mathrm{odd};2)={\sigma }_1(\mathrm{odd})$. Since ${\sigma }_3(2M)=9{\sigma }_3(M)-8{\sigma }_3(\frac{M}{2})$, the right-hand side of (36) is

$$\begin{array}{c}=\sum _{M=1}^{N-1}{\sigma }_1(2N-1-2M)\{{\sigma }_3(M)-{\sigma }_3\left(\frac{M}{2}\right)\}\hfill \\ =\sum _{M=1}^{N-1}{\sigma }_1(2N-1-2M){\sigma }_3(M)-\sum _{M<\frac{2N-1}{4}}{\sigma }_1(2N-1-4M){\sigma }_3(M)\hfill \\ =\frac{1}{240}({\sigma }_5(2N-1)-{\sigma }_1(2N-1))\hfill \\ \phantom{=}-\{\frac{1}{3\text{,}840}{\sigma }_5(2N-1)-\frac{1}{240}{\sigma }_1(2N-1)+\frac{1}{256}a(2N-1)\}\hfill \end{array}$$

by [[25], Theorem 6] and in [[28], Theorem 4.1(iii)] which state that

$$\begin{array}{c}\sum _{m<N/2}{\sigma }_3(m){\sigma }_1(N-2m)\hfill \\ =\frac{1}{240}({\sigma }_5(N)-\sigma (N)+20{\sigma }_5\left(\frac{N}{2}\right)+(10-30N){\sigma }_3\left(\frac{N}{2}\right))\hfill \end{array}$$

(37)

and

$$\begin{array}{rcl}\sum _{m<N/4}{\sigma }_3(m){\sigma }_1(N-4m)& =& \frac{1}{3\text{,}840}{\sigma }_5(N)+\frac{1}{256}{\sigma }_5\left(\frac{N}{2}\right)+\frac{1}{12}{\sigma }_5\left(\frac{N}{4}\right)\\ +\frac{1-3N}{24}{\sigma }_3\left(\frac{N}{4}\right)-\frac{1}{240}{\sigma }_1(N)+\frac{1}{256}a(N)\end{array}$$

(38)

respectively. This completes the proof. □

Proof of Corollary 1.4

We note that

$$\begin{array}{c}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}(2n-1){\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\frac{1}{3}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}(2(n+l+m-1)-1){\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\frac{1}{3}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}(2N-1){\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2).\hfill \end{array}$$

Therefore, from Theorem 1.3, we obtain

$$\begin{array}{c}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}n{\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\frac{N+1}{3}\underset{n,l,m\ge 1}{\sum _{n+l+m-1=N}}{\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l-1;2){\sigma }_{1,1}(2m-1;2)\hfill \\ =\frac{N+1}{768}({\sigma }_5(2N-1)-a(2N-1)).\hfill \end{array}$$

Thus, the first assertion

follows.

We note that $768=2^8\cdot 3$, and thus whenever and $N+1$ is odd, we have $(N+1,768)=1$. Thus,

whenever . This proves the second assertion. □

Proof of Theorem 1.5

We note that

$$\begin{array}{rcl}{S}_1{S}_2^2& =& \sum _{n,l,m=1}^{\mathrm{\infty }}{\sigma }_{1,1}(2n-1;2){\sigma }_{1,1}(2l;2){\sigma }_{1,1}(2m;2)q^{2(n+l+m)-1}\\ =& \sum _{N=3}^{\mathrm{\infty }}\{\sum _{M=2}^{N-1}\sum _{m=1}^{M-1}{\sigma }_{1,1}(2N-1-2M;2){\sigma }_{1,1}(2M-2m;2){\sigma }_{1,1}(2m;2)\}{q}^{2N-1}.\end{array}$$

Thus, by ${\sigma }_{1,1}(2m;2)={\sigma }_{1,1}(m;2)$ and [[27], (11)], we obtain that

$$\begin{array}{c}\sum _{M=2}^{N-1}\sum _{m=1}^{M-1}{\sigma }_{1,1}(2N-1-2M;2){\sigma }_{1,1}(2M-2m;2){\sigma }_{1,1}(2m;2)\hfill \\ =\sum _{M=2}^{N-1}{\sigma }_{1,1}(2N-1-2M;2)\{\sum _{m=1}^{M-1}{\sigma }_{1,1}(M-m;2){\sigma }_{1,1}(m;2)\}\hfill \\ =\sum _{M=2}^{N-1}{\sigma }_1(2N-1-2M)\left\{\frac{1}{24}(11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2))\right\}.\hfill \end{array}$$

(39)

We observe that

$$\begin{array}{c}11{\sigma }_3(M)-{\sigma }_3(2M)-2{\sigma }_{1,1}(M;2)\hfill \\ =11{\sigma }_3(M)-\{9{\sigma }_3(M)-8{\sigma }_3\left(\frac{M}{2}\right)\}-2\{{\sigma }_1(M)-2{\sigma }_1\left(\frac{M}{2}\right)\}\hfill \\ =2{\sigma }_3(M)+8{\sigma }_3\left(\frac{M}{2}\right)-2{\sigma }_1(M)+4{\sigma }_1\left(\frac{M}{2}\right).\hfill \end{array}$$

Thus, the right-hand side of (39) is

$$\begin{array}{c}=\frac{1}{24}[2\sum _{M=1}^{N-1}{\sigma }_1(2N-1-2M){\sigma }_3(M)+8\sum _{M<\frac{2N-1}{4}}{\sigma }_1(2N-1-4M){\sigma }_3(M)\hfill \\ \phantom{=}-2\sum _{M=1}^{N-1}{\sigma }_1(2N-1-2M){\sigma }_1(M)+4\sum _{M<\frac{2N-1}{4}}{\sigma }_1(2N-1-4M){\sigma }_1(M)].\hfill \end{array}$$

Now from (37), (38) and (see [[25], (4.4)]), we have

$$\begin{array}{c}\sum _{m<N/2}\sigma (m)\sigma (N-2m)\hfill \\ =\frac{1}{24}(2{\sigma }_3(N)+(1-3N){\sigma }_1(N)+8{\sigma }_3\left(\frac{N}{2}\right)+(1-6N)\sigma \left(\frac{N}{2}\right))\hfill \end{array}$$

and from (see [[25], Theorem 4]), we have

$$\begin{array}{c}\sum _{m<N/4}\sigma (m)\sigma (N-4m)\hfill \\ =\frac{1}{48}({\sigma }_3(N)+(2-3N){\sigma }_1(N)+3{\sigma }_3\left(\frac{N}{2}\right)+16{\sigma }_3\left(\frac{N}{4}\right)+(2-12N){\sigma }_1\left(\frac{N}{4}\right)).\hfill \end{array}$$

Thus, the theorem follows. □