- Research
- Open access
- Published:
An inertially constructed forward–backward splitting algorithm in Hilbert spaces
Advances in Difference Equations volume 2021, Article number: 124 (2021)
Abstract
In this paper, we develop an iterative algorithm whose architecture comprises a modified version of the forward–backward splitting algorithm and the hybrid shrinking projection algorithm. We provide theoretical results concerning weak and strong convergence of the proposed algorithm towards a common solution of the fixed point problem associated to a finite family of demicontractive operators, the split equilibrium problem and the monotone inclusion problem in Hilbert spaces. Moreover, we compute a numerical experiment to show the efficiency of the proposed algorithm. As a consequence, our results improve various existing results in the current literature.
1 Introduction
The theory of mathematical optimization provides a quantitative optimal solution associated with various real-world problems emerging in the fields of engineering, medicine, economics, management, and industry and other branches of the sciences. One of the main advantages of mathematical optimization is to provide effective iterative algorithms and the corresponding analysis of these iterative algorithms. Moreover, the viability of such iterative algorithms is evaluated in terms of computational performance and complexity. As a consequence, the theory of mathematical optimization has not only emerged as an independent subject to solve real-world problems but also serve as an interdisciplinary bridge between various branches of sciences.
Monotone operator theory is a fascinating field of research in nonlinear functional analysis and found valuable applications in the field of convex optimization, subgradients, partial differential equations, variational inequalities, signal and image processing, evolution equations and inclusions; see, for instance, [4, 12, 14, 30] and the references cited therein. It is noted that the convex optimization problem can be translated into finding a zero of a maximal monotone operator defined on a Hilbert space. On the other hand, the problem of finding a zero of the sum of two (maximal-) monotone operators is of fundamental importance in convex optimization and variational analysis [23, 27, 33]. The forward–backward algorithm is prominent among various splitting algorithms to find a zero of the sum of two maximal monotone operators [23]. The class of splitting algorithms has parallel computing architectures and thus reducing the complexity of the problems under consideration. On the other hand, the forward–backward algorithm efficiently tackle the situation for smooth and/or nonsmooth functions. It is worth mentioning that the forward–backward algorithm has been modified by employing the heavy ball method [28] for convex optimization problems.
Fixed point theory has been studied extensively in the current literature owing to its rich abstract structures. These structures and subsequent tools elegantly manipulate various mathematical problems from the areas such as control theory, game theory, mathematical economics, image recovery signal processing and image processing. In 2015, the problem of finding a common solution of the zero point problem and fixed point problem was studied by Takahashi et al. [32]. It is well known that the class of demicontractive operators [15] includes various classes of nonlinear operators and comparatively exhibits powerful applications. Therefore, it is natural to study the fixed point problems associated with the class of demicontractive operators.
The theory of equilibrium problems is a systematic approach to the study of a diverse range of problems arising in the field of physics, optimization, variational inequalities, transportation, economics, network and noncooperative games; see, for example, [5, 11–13] and the references cited therein. The classical equilibrium problem theory has been generalized in several interesting ways to solve real-world problems. In 2012, Censor et al. [9] proposed a theory regarding split variational inequality problem (SVIP) which aims to solve a pair of variational inequality problems in such a way that the solution of a variational inequality problem, under a given bounded linear operator, solves another variational inequality.
In 2011, Moudafi [26] suggested the concept of split monotone variational inclusions (SMVIP) which includes, as a special case, split variational inequality problem, split common fixed point problem, split zeros problem, split equilibrium problem (SEP) and split feasibility problem. These problems have already been studied and successfully employed as a model in intensity-modulated radiation therapy treatment planning; see [6, 8]. This formalism is also at the core of modeling of many inverse problems arising for phase retrieval and other real-world problems; for instance, in sensor networks in computerized tomography and data compression; see, for example, [10, 12]. Some methods have been proposed and analyzed to solve SEP and generalized SEP in Hilbert spaces; see, for example, [2, 3, 16–22] and the references cited therein.
Inspired and motivated by the above-mentioned results and the ongoing research in this direction, we aim to employ the modified inertial forward–backward algorithm to find a common solution of fixed point problem associated to a finite family of demicontractive operators, SEP and monotone inclusion problem in Hilbert spaces. The rest of the paper is organized as follows: Section 2 contains preliminary concepts and results regarding fixed point theory, equilibrium problem theory and monotone operator theory. Section 3 comprises weak and strong convergence results of the proposed algorithm. Section 4 deals with the efficiency of the proposed algorithm by a numerical experiment together with theoretical applications to the split feasibility problem, the split variational inequality problem and the split minimization problem.
2 Preliminaries
In this section, we recall concepts and results regarding fixed point theory, equilibrium problem theory and monotone operator theory. Throughout this paper, let \(\mathcal{H}_{1}\) be a real Hilbert space with the inner product and the associated norm \(\langle \cdot , \cdot \rangle \) and \(\Vert \cdot \Vert \), respectively. The symbols ⇀ and → denotes weak and strong convergence.
An operator \(P_{C}\) is said to be metric projection of \(\mathcal{H}_{1}\) onto nonempty, closed and convex subset C, if for every \(x \in \mathcal{H}_{1}\), there exists a unique nearest point in C denoted by \(P_{C}x\) such that
It is noted that \(P_{C}\) is a firmly nonexpansive operator and \(P_{C}x\) is characterized by the following property:
Next, we recall the definitions of nonexpansive and related operators.
Definition 1
([4])
Let C be a nonempty subset of \(\mathcal{H}_{1}\), for an operator \(T:C \rightarrow \mathcal{H}_{1}\), we denote by \(Fix(T)\) the set of fixed points of the operator T, that is, \(Fix(T)=\{x \in \mathcal{H}_{1}| x=Tx\}\). The operator T is considered as:
-
1.
nonexpansive if
$$ \Vert Tx-Ty \Vert \leq \Vert x-y \Vert , \quad \forall x,y \in C; $$ -
2.
firmly nonexpansive if
$$ \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}- \bigl\Vert (Id-T)x-(Id-T)y \bigr\Vert ^{2}, \quad \forall x,y \in C; $$ -
3.
quasi-nonexpansive if \(Fix(T)\neq \emptyset \) such that
$$ \Vert Tx-y \Vert \leq \Vert x-y \Vert , \quad \forall x \in C, y \in Fix(T); $$ -
4.
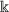 -demicontractive if \(Fix(T)\neq \emptyset \) and there exists
-demicontractive if \(Fix(T)\neq \emptyset \) and there exists 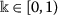 such that
such that 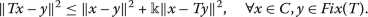
It follows immediately that a firmly nonexpansive operator is a nonexpansive operator.
We now define the concept of SEP. Let \(\hbar :\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}\) be a bounded linear operator. Let \(F_{1}:C\times C\rightarrow \mathbb{R}\) and \(F_{2}:Q\times Q\rightarrow \mathbb{R}\) be two bifunctions, then SEP is to find:
and
The solution set of the SEP (1) and (2) is denoted by
Now, we recall some important concepts related to monotone operator theory [4].
Let \(\mathcal{A}: \mathcal{H}_{1} \rightarrow 2^{\mathcal{H}_{1}}\) be a set-valued operator. We denote its domain, range, graph and zeros by \(Dom \mathcal{A}=\{x \in \mathcal{H}_{1}| \mathcal{A}x \neq 0\}\), \(Ran\mathcal{A}=\{ u \in \mathcal{H}_{1}| (\exists x \in \mathcal{H}_{1})u \in \mathcal{A}x\}\), \(Gra\mathcal{A}=\{(x,u) \in \mathcal{H}_{1}\times \mathcal{H}_{1}| u \in \mathcal{A}x\}\) and \(Zer\mathcal{A}=\{x \in \mathcal{H}_{1}| 0 \in \mathcal{A}x\}\), respectively. Let the set-valued operator \(\mathcal{A}\) is said to be monotone, if
Moreover, \(\mathcal{A}\) is said to be maximal monotone if its graph is not strictly contained in the graph of any other monotone operator on \(\mathcal{H}_{1}\). A well-known example of a maximal monotone operator is the subgradient operator of a proper, lower semicontinuous convex function \(f:\mathcal{H}_{1} \rightarrow (-\infty ,+\infty ]\) defined by
For a maximal monotone operator, the associated resolvent operator with index \(m > 0\) is defined as
where Id denotes the identity operator.
It is well known that the resolvent operator \(J_{m}\) is well-defined everywhere on Hilbert space \(\mathcal{H}_{1}\). Furthermore, \(J_{m}\) is single-valued and satisfies the firmly nonexpansiveness. Furthermore, \(x \in \mathcal{A}^{-1}(0)\) if and only if \(x=J_{m}(x)\).
Let \(f:\mathcal{H}_{1}\rightarrow \mathbb{R}\cup \{ +\infty \} \) be a proper, convex and lower semicontinuous function and let \(g:\mathcal{H}_{1}\rightarrow \mathbb{R}\) be a convex, differentiable and Lipschitz continuous function, then the convex minimization problem for f and g is defined as
Definition 2
([4])
Let \(\mathcal{B}:\mathcal{H}_{1} \rightarrow \mathcal{H}_{1}\) be a nonlinear operator. For \(\gamma > 0\), the operator \(\mathcal{B}\) is said to be γ-inverse strongly monotone (γ-ism) if
The γ-ism is also coined as γ-cocoercive operator. Moreover, γ-ism is \(\frac{1}{\gamma }\)-Lipschitz continuous. In connection with the problem (4), the monotone inclusion problem with respect to a maximally monotone operator \(\mathcal{A}\) and an arbitrary operator \(\mathcal{B}\) is to find:
In the sequel, we list some important results in the form of lemmas for the convergence analysis.
Lemma 2.1
([4])
Let C be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal{H}_{1}\). Let \(T: C \rightarrow C\) be an operator. Then the operator T is said to be demiclosed at zero, if for any sequence \((x_{k})\) in C that converges weakly to x and \((Id-T)x_{k}\) converges strongly to zero, then \(x \in Fix(T)\).
Lemma 2.2
Let \(x,y \in \mathcal{H}_{1}\) and \(\beta \in \mathbb{R}\), then the following relations hold:
-
\(\Vert x+y \Vert ^{2} \leq \Vert x \Vert ^{2}+2 \langle y, x+y \rangle \);
-
\(\Vert \beta x+(1-\beta )y \Vert ^{2}=\beta \Vert x \Vert ^{2}+(1-\beta ) \Vert x \Vert ^{2}- \beta (1-\beta ) \Vert x-y \Vert ^{2}\).
Lemma 2.3
([31])
Let E be a Banach space satisfying Opial’s condition and let \(\{x_{n}\}\) be a sequence in E. Let \(l,m\in E\) be such that \(\lim_{n\rightarrow \infty } \Vert x_{n}-l \Vert \) and \(\lim_{n\rightarrow \infty } \Vert x_{n}-m \Vert \) exist. If \(\{x_{n_{k}}\}\) and \(\{x_{m_{k}}\}\) are subsequences of \(\{x_{n}\}\) which converge weakly to l and m, respectively, then \(l=m\).
Lemma 2.4
([24])
Let E be a Banach space. Let \(\mathcal{A}:E\rightarrow 2^{E}\) be an m-accretive operator and let \(\mathcal{B}:E\rightarrow E\) be an α-inverse strongly accretive operator. Then we have
-
a)
For \(r > 0\), \(Fix(T^{\mathcal{A},\mathcal{B}}_{r})=(\mathcal{A}+\mathcal{B})^{-1}(0)\),
-
b)
for \(0 < s \leq r \) and \(x \in E\), \(\Vert x-T^{\mathcal{A},\mathcal{B}}_{s}x \Vert \leq 2 \Vert x-T^{\mathcal{A},\mathcal{B}}_{r} \Vert \).
Lemma 2.5
([24])
Let E be a uniformly convex and q-uniformly smooth Banach space for some \(q\in (0,2]\). Let \(\mathcal{A}:E\rightarrow 2^{E}\) be an m-accretive operator and let \(\mathcal{B}:E\rightarrow E\) be an α-inverse strongly accretive operator. Then, given \(r>0\), there exists a continuous, strictly increasing and convex function \(\varphi _{q}:\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}\) with \(\varphi _{q}(0)=0\) such that for all \(x,y\in B_{r}\)
where \(k_{q}\) is the q-uniform smoothness coefficient of E.
Lemma 2.6
([1])
Let \(\{\xi _{n}\}\), \(\{\eta _{n}\}\) and \(\{\alpha _{n}\}\) be sequences in \([0,+\infty )\) satisfying
provided that \(\sum_{n=1}^{\infty }\eta _{n}<+\infty \) and \(0\leq \alpha _{n}\leq \alpha <1\) for all \(n\geq 1\). Then the following two relations hold:
Lemma 2.7
([25])
Let C be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal{H}_{1}\). For every \(x,y\in \mathcal{H}_{1}\) and \(a\in \mathbb{R}\), the set
is closed and convex.
Assumption 2.8
Let C be a nonempty, closed and convex subset of a Hilbert space \(\mathcal{H}_{1}\). Let \(F_{1}:C\times C\rightarrow \mathbb{R}\) be a bifunction satisfying the following conditions:
-
(A1):
\(F_{1}(x,x)=0\) for all \(x\in C\);
-
(A2):
\(F_{1}\) is monotone, i.e., \(F_{1}(x,y)+F_{1}(y,x)\leq 0\) for all \(x,y \in C\);
-
(A3):
for each \(x,y,z\in C\), \(\limsup_{t\rightarrow 0}F_{1}(tz+(1-t)x,y)\leq F_{1}(x,y)\);
-
(A4):
for each \(x\in C\), \(y\mapsto F_{1}(x,y)\) is convex and lower semicontinuous.
Lemma 2.9
([11])
Let C be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal{H}_{1}\) and let \(F_{1}:C\times C\rightarrow \mathbb{R}\) be a bifunction satisfying Assumption 2.8. For \(r>0\) and \(x\in \mathcal{H}_{1}\), there exists \(z\in C\) such that
Moreover, define an operator \(T_{r}^{F}:\mathcal{H}_{1}\rightarrow C\) by
for all \(x\in \mathcal{H}_{1}\). Then we have the following observations:
-
(1):
for each \(x \in \mathcal{H}_{1}\), \(T_{r}^{F_{1}}(x)\neq \emptyset \);
-
(2):
\(T_{r}^{F_{1}}\) is single-valued;
-
(3):
\(T_{r}^{F_{1}}\) is firmly nonexpansive;
-
(4):
\(Fix(T_{r}^{F_{1}})=EP(F_{1})\);
-
(5):
\(EP(F_{1})\) is closed and convex.
It is noted that if \(F_{2}:Q\times Q\rightarrow \mathbb{R}\) is a bifunction satisfying Assumption 2.8, where Q is a nonempty, closed and convex subset of a Hilbert space \(\mathcal{H}_{2}\). Then, for each \(s>0\) and \(w \in \mathcal{H}_{2}\), we define the operator
Similarly, we have the following relations:
-
(1):
for each \(w \in \mathcal{H}_{2}\), \(T_{s}^{F_{2}}(w)\neq \emptyset \);
-
(2):
\(T_{s}^{F_{2}}\) is single-valued;
-
(3):
\(T_{s}^{F_{2}}\) is firmly nonexpansive;
-
(4):
\(Fix(T_{s}^{F_{2}})=EP(F_{2})\);
-
(5):
\(EP(F_{2})\) is closed and convex.
3 Algorithm and convergence analysis
In this section, we present an approach to the convergence analysis of inertial forward–backward splitting method for solving the fixed point problem associated to a finite family of demicontractive operators, SEP and monotone inclusion problem in Hilbert spaces. First, we set the following hypotheses required in the sequel: Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two real Hilbert spaces and let \(C \subseteq \mathcal{H}_{1}\), \(Q \subseteq \mathcal{H}_{2}\) be nonempty, closed and convex subsets of Hilbert spaces \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. We consider the following hypotheses:
-
(H1)
Let \(F_{1}: C \times C \rightarrow \mathbb{R}\) and \(F_{2}: Q \times Q \rightarrow \mathbb{R}\) be two bifunctions satisfying Assumption 2.8 such that \(F_{2}\) is upper semicontinuous;
-
(H2)
let \(\hbar : \mathcal{H}_{1} \rightarrow \mathcal{H}_{2}\) be a bounded linear operator;
-
(H3)
let \(\mathcal{A}:\mathcal{H}_{1} \rightarrow 2^{\mathcal{H}_{1}}\) be a maximal monotone operator and let \(\mathcal{B}:\mathcal{H}_{1} \rightarrow \mathcal{H}_{1}\) be a γ-ism operator;
-
(H4)
for \(i \in \{1,2,\ldots ,N\}\), let \(S_{i}:\mathcal{H}_{1} \rightarrow \mathcal{H}_{1}\) be a finite family of
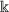 -demicontractive operators;
-demicontractive operators; -
(H5)
suppose that \(\Gamma := zer(\mathcal{A}+\mathcal{B})\cap \Omega \cap \bigcap^{i=1}_{N}Fix(S_{i})\).
Theorem 3.1
If \(\Gamma \neq \emptyset \) with hypotheses (H1)–(H5), then the sequence \((x_{k})\) generated by Algorithm 1 converges weakly to an element \(\bar{x} \in \Gamma \), provided the following conditions hold:
-
(C1)
\(\sum^{\infty }_{k=1}\Theta _{k} \Vert x_{k}-x_{k-1} \Vert <\infty \);
-
(C2)
\(0 < a^{\ast } \leq \beta _{k}\), \(\lambda _{k} \leq b^{\ast } < 1\) and
 ;
; -
(C3)
\(0 < \liminf_{k \rightarrow \infty } \lambda _{k} \leq \limsup_{k \rightarrow \infty }\lambda _{k} < 1\);
-
(C4)
\(\liminf_{k \rightarrow \infty }u_{k} > 0\);
-
(C5)
\(0 < \liminf_{k \rightarrow \infty } m_{k} \leq \limsup_{k \rightarrow \infty } m_{k} < 2\gamma \).
Proof
First we show that \(\hbar ^{\ast }(Id-T_{u_{k}}^{F_{2}})\hbar \) is an \(\frac{1}{L}\)-ism operator. For this, we utilize the firmly nonexpansiveness of \(T_{u_{k}}^{F_{2}}\), which implies that \((Id-T_{u_{k}}^{F_{2}})\) is an 1-ism operator. Now, observe that
for all \(x,y\in \mathcal{H}_{1}\). So, we observe that \(\hbar ^{\ast }(Id-T_{u_{k}}^{F_{2}})\hbar \) is an \(\frac{1}{L}\)-ism. Moreover, \(Id-\delta \hbar ^{\ast }(Id-T_{u_{k}}^{F_{2}})h\) is nonexpansive provided \(\delta \in (0,\frac{1}{L})\). Now, we divided the rest of the proof into the following three steps:
Step 1. Show that \(\lim_{k\rightarrow \infty } \Vert x_{k}-\hat{x} \Vert \) exists for every \(\hat{x}\in \Gamma \).
For any \(\hat{x}\in \Gamma \), we get
Since \(T^{F_{1}}_{u_{k}} \hat{x}=\hat{x}\) and using (6), we have
Thus, we have
Moreover, we have
Note that
Since \(\delta \in (0 , \frac{1}{L})\), the estimate (11) implies that
Furthermore, by using (6), (12) and (C2), we have

Moreover, it follows from (6), (12), (13) and Lemma 2.5 that
From Lemma 2.6 and (C1), we conclude from the estimate (14) that \(\lim_{k\rightarrow \infty } \Vert x_{k}-\hat{x} \Vert \) exists.
Step 2. Show that \(x_{k}\rightharpoonup \bar{x}\in (\mathcal{A}+\mathcal{B})^{-1}(0)\).
Since \(\hat{x}=J_{k}\hat{x}\), therefore it follows from Lemma 2.2 and Lemma 2.5 that

As \(\lim_{k\rightarrow \infty } \Vert x_{k}-\hat{x} \Vert \) exists, therefore utilizing, (C1), (C4), (C5) and (15), we get
Also from (15), we get
Using (16), (17) and the triangle inequality
we get
Since \(\liminf_{k\rightarrow \infty }m_{k}>0\) there exists \(m>0\) such that \(m_{k}\geq m\) for all \(k\geq 0\). It follows from Lemma 2.4(b) that
Now utilizing (18), the above estimate implies that
As a consequence, we have
Again, from (15), we have

Rearranging the above estimate and using (C1), (C2), we get
This implies that
Again, by Lemma 2.2, Lemma 2.6 and (11), we have
Rearranging the above estimate, we have
Since \(\delta (L\delta -1)<0\), it follows from (C1) and (23) that
Note that \(T^{F_{1}}_{u_{k}}\) is firmly nonexpansive and \(Id-\delta \hbar ^{\ast }(Id-T^{F_{2}}_{u_{k}})\hbar \) is nonexpansive, therefore we have
So, we have
Therefore, we have
Utilizing (24) and (C2), we have
From the definition of \((b_{k})\) and (27), we have
By the definition of \((b_{k})\) and (C1), we have
Since \((x_{k})\) is bounded and \(\mathcal{H}_{1}\) is reflexive, \(\nu _{\omega }(x_{k})=\{x\in \mathcal{H}_{1}:x_{k_{n}} \rightharpoonup x,(x_{k_{n}})\subset (x_{k})\}\) is nonempty. Let \(\bar{x}\in \nu _{\omega }(x_{{k}})\) be an arbitrary element. Then there exists a subsequence \((x_{k_{n}})\subset (x_{k})\) converging weakly to x̄. Let \(\hat{x}\in \nu _{\omega }(x_{k})\) and \((x_{k_{m}})\subset (x_{k})\) be such that \(x_{k_{m}}\rightharpoonup \hat{x}\). From (24), we also have \(\ell _{k_{n}}\rightharpoonup \bar{x}\) and \(\ell _{k_{m}}\rightharpoonup \hat{x}\). Since \(T_{m}^{\mathcal{A},\mathcal{B}}\) is nonexpansive, from (19) and Lemma 2.1, we have \(\hat{x},\bar{x}\in (\mathcal{A}+\mathcal{B})^{-1}(0)\). By applying Lemma 2.3, we obtain \(\hat{x}=\bar{x}\).
Step 3. Show that \(\bar{x} \in \Omega \).
Let \(\bar{x} \in EP(F_{1})\). For any \(y\in \mathcal{H}_{1}\), we have
This implies that
From Assumption 2.8(A2), we have
So, we have
Utilizing (28) and (C2), we get \(\ell _{k_{n}} \rightharpoonup \bar{x}\). Moreover, from (24) and Assumption 2.8(A4), we get
Let \(y_{t}=ty+(1-t)\bar{x}\) for some \(1 \geq t > 0\) and \(y \in \mathcal{H}_{1}\). Since \(\bar{x} \in \mathcal{H}_{1}\), consequently, \(y_{t} \in \mathcal{H}_{1}\) and hence \(F_{1}(y_{t},\bar{x})\leq 0\). Using Assumption 2.8((A1) and (A4)), it follows that
This implies that
Letting \(t \rightarrow 0\), we have
Thus, \(\bar{x} \in EP(F_{1})\). Similarly, we can show that \(\bar{x} \in EP (F_{2})\). Since ħ is a bounded linear operator, we have \(\hbar x_{k_{n}} \rightharpoonup \hbar \bar{x}\). It follows from (26) that
Now, from Lemma 2.7 we have
for all \(y \in \mathcal{H}_{1}\). Since \(F_{2}\) is upper semicontinuous in the first argument and from (31), we have
for all \(y \in \mathcal{H}_{1}\). This implies that \(\hbar \bar{x} \in EP(F_{2})\). Therefore, \(\bar{x} \in \Omega \).
Step 4. From (21) and by using the demiclosed principle for \(S_{i}\) (it is evident that \(x_{k_{n}} \rightharpoonup \bar{x}\) and \(\lim_{k \rightarrow \infty } \Vert (Id-S_{i})x_{k_{n}} \Vert =0\)), we have \(\bar{x} \in \bigcap^{i=1}_{N}Fix(S_{i})\) and hence \(\bar{x} \in \Gamma \). This completes the proof. □
Now, we establish strong convergence results of Algorithm 2.
Theorem 3.2
If \(\Gamma \neq \emptyset \) with hypotheses (H1)–(H5), then the sequence \((x_{k})\) generated by Algorithm 2 converges strongly to an element \(\bar{x} \in P_{\Gamma }x_{1}\), provided the conditions (C1)–(C5) hold.
Proof
The proof is divided into the following steps:
Step 1. Show that the sequence \(\{ x_{k} \} \) defined in Algorithm 2 is well-defined.
We know that \((\mathcal{A}+\mathcal{B})^{-1}(0)\), Ω and \(Fix(S_{i})\) are closed and convex by Lemma 2.4 and Lemma 2.9. Moreover, from Lemma 2.7 we see that \(C_{k+1}\) is closed and convex for each \(k\geq 1\). Hence the projection \(P_{C_{k+1}}x_{1}\) is well-defined. For any \(\hat{x}\in \Gamma \), it follows from Algorithm 2 and the estimates (6), (12) and (13) that

It follows from the estimate (32) that \(\Gamma \subset C_{k+1}\). Summing up these facts, we conclude that \(C_{k+1}\) is nonempty, closed and convex for all \(k \geq 1\), and hence the sequence \((x_{k})\) is well-defined.
Step 2. Show that \(\lim_{k\rightarrow \infty } \Vert x_{k}-x_{1} \Vert \) exists.
Since Γ is nonempty closed and convex subset of \(\mathcal{H}_{1}\), there exists a unique \(x^{\ast }\in \Gamma \) such that \(x^{\ast }=P_{\Gamma }x_{1}\). From \(x_{k+1}=P_{C_{k+1}}x_{1}\), we have \(\Vert x_{k+1}-x_{1} \Vert \leq \Vert x^{\ast }-x_{1} \Vert \), for all \(\bar{x}\in \Gamma \subset C_{k+1}\). In particular \(\Vert x_{k+1}-x_{1} \Vert \leq \Vert P_{\Gamma }x_{1}-x_{1} \Vert \). This proves that the sequence \((x_{k})\) is bounded. On the other hand, from \(x_{k}=P_{C_{k}}x_{1}\) and \(x_{k+1}=P_{C_{k+1}}x_{1}\in C_{k+1}\), we get
This implies that \((x_{k})\) is nondecreasing and hence
Step 3. Show that \(\bar{x}\in (\mathcal{A}+\mathcal{B})^{-1}(0)\).
In order to proceed, we first calculate the following estimates which are required in the sequel:
Taking limsup on both sides of the above estimate and utilizing (33), we have \(\limsup_{k\rightarrow \infty } \Vert x_{k+1}-x_{k} \Vert ^{2}=0\). That is,
Note that \(x_{k+1}\in C_{k+1}\), therefore we have
Utilizing (34) and (C1), the above estimate implies that
From (34), (35) and the triangular inequality
we get
Also, from Lemma 2.2 and (21), we have

Rearranging the above estimate, we have
The above estimate, by using (C1) and (36), implies that
Making use of (37), we have the following estimate:
Reasoning as above, utilizing the estimate (37), the estimate (38) implies that
In a similar fashion, we have
Reasoning as above (Theorem 3.1, Step 2), we have the desired result.
Step 4. Show that \(\bar{x}\in \Omega \).
See proof of Step 3 in Theorem 3.1.
Step 5. Show that \(\bar{x}\in \bigcap^{i=1}_{N}Fix(S_{i})\).
See proof of Step 4 in Theorem 3.1.
Step 6. Show that \(\bar{x}=P_{\Gamma }x_{1}\).
Let \(x=P_{\Gamma }x_{1}\) imply that \(x=P_{\Gamma }x_{1}\in C_{k+1}\). Since \(x_{k+1}=P_{C_{k+1}}x_{1}\in C_{k+1}\), we have
On the other hand, we have
That is,
Therefore, we conclude that \(\lim_{k\rightarrow \infty }x_{k}=\bar{x}=P_{\Gamma }x_{1}\). This completes the proof. □
The following remark gives us a stopping criterion of Algorithm 2.
Remark 3.3
We remark here that the condition (C1) is easily implemented in numerical computation since the value of \(\Vert x_{k}-x_{k-1} \Vert \) is known before choosing \(\Theta _{k}\). The parameter \(\Theta _{k}\) can be taken as \(0 \leq \Theta _{k} \leq \widehat{\Theta _{k}}\),
where \(\{ \nu _{k}\}\) is a positive sequence such that \(\sum^{\infty }_{k = 1}\nu _{k} < \infty \) and \(\Theta _{k} = \Theta \in [0,1)\).
4 Numerical experiment and results
This section shows the effectiveness of Algorithm 2 by the following given example.
Example 4.1
Let \(\mathcal{H}_{1} = \mathcal{H}_{2} = \mathbb{R}\) be the set of all real numbers, with the inner product defined by \(\langle x , y\rangle = xy\), for all \(x , y \in \mathbb{R}\) and the usual induced norm \(\vert \cdot \vert \). Let \(F_{1}:\mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\) be a bifunction defined as \(F_{1}(x,y)=2x(y-x)\) and let \(F_{2}:\mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\) be a bifunction defined as \(F_{2}(p,q)=p(q-p)\). For all \(x \in \mathbb{R}\), let the operators \(\hbar ,\mathcal{A},\mathcal{B} : \mathbb{R}\rightarrow \mathbb{R}\) be defined as \(\hbar (x)=3x\), \(\mathcal{A}x=4x\) and \(\mathcal{B}x=3x\), respectively. Let \(S_{i}: \mathbb{R} \rightarrow \mathbb{R}\) be a finite family of demicontractive operators defined by
Then the sequence \((x_{k})\) generated by Algorithm 2 strongly converges to a point in Γ.
Proof
It is easy to prove that the bifunctions \(F_{1}\) and \(F_{2}\) satisfy Assumptions 2.8 and \(F_{2}\) is upper semicontinuous with \(\Omega = 0\). Moreover, ħ is bounded linear operator on \(\mathbb{R}\) with the adjoint operator \(\hbar ^{\ast }\) such that \(\Vert \hbar \Vert = \Vert \hbar ^{\ast } \Vert =3\), \(\mathcal{A}\) is a maximal monotone operator and \(\mathcal{B}\) is a monotone and γ-Lipschitz operator for some \(\gamma > 0\) with \((\mathcal{A} + \mathcal{B})^{-1}(0)=\{0\}\). Note that \(S_{i}\) is a finite family of \(\frac{1-i^{2}}{(1+i)^{2}}\)-demicontractive operators with \(\bigcap^{i=1}_{N}Fix(S_{i})=\{0\}\). Hence \(\Gamma = (\mathcal{A} + \mathcal{B})^{-1}(0)\cap \Omega \cap \bigcap^{i=1}_{\infty }Fix(S_{i}) = 0\). Choose \(\Theta = 0.5\), \(u_{k}=\frac{k}{5k+1}\), \(\beta _{k}=\frac{1}{100k+1}\), \(\lambda _{k} =\frac{1}{100k+1}\), \(\delta =0.04\), \(L=3\) and \(m=0.01\). Since
For the rest of the numerical experiment, we proceed as follows:
Step 1. Find \(z \in F_{2}\) such that \(F_{2}(z,y)+\frac{1}{u}\langle y - z,z - \hbar x \rangle \geq 0\) for all \(y \in F_{2}\). We write
for all \(y \in F_{2}\). Thus, by Lemma 2.9(2), we know that \(T^{F_{2}}_{u}\hbar x \) is single-valued for each \(x \in F_{1}\). Hence \(z=\frac{\hbar x}{1+u}\).
Step 2. Find \(g \in F_{1}\) such that \(g = x-\delta \hbar ^{\ast }(I-T_{r}^{F_{2}})\hbar x\). From Step 1, we get
Step 3. Find \(p \in F_{1}\) such that \(F_{1}(p,q)+\frac{1}{u}\langle p-q,p-g\rangle \geq 0\) for all \(q \in F_{1}\). From Step 2, we have
for all \(q \in F_{1}\). Similarly, by Lemma 2.9(2), we obtain \(p=\frac{g}{1+2u}=\frac{(1-3\delta )x}{1+2u}+ \frac{3\delta \hbar x}{(1+u)(1+2u)}\).
Step 4. Compute the numerical results for \(x_{k+1}\).
We provide a numerical test of a comparison between our Inertial Forward–Backward Splitting Algorithm (IFBSA) defined in Algorithm 2 (i.e., \(\Theta _{k}\neq 0\)) and the Forward–Backward Splitting Algorithm (FBSA) (i.e., \(\Theta _{k}=0\)). The stopping criterion is defined as \(\mathrm{Error}= E_{k}= \Vert x_{k+1}-x_{k} \Vert <10^{-6}\). The different choices of \(x_{0}\) and \(x_{1}\) are given in tables and figures.
The error plotting \(E_{k}\) and \((x_{k})\) against \(\Theta _{k} \neq 0\) and \(\Theta _{k}=0\) for each choice in Table 1 is shown in Fig. 1.
□
We can see from Table 1 and Figs. 1 and 2 that IFBSA performs better as compared to FBSA. Elaborating the behavior of this algorithm with respect to Table 1, the error analysis is depicted in Figs. 1 and 2 whereas the number of iterations required to converge the sequence \((x_{k})\) towards the common solution are expressed in Figs. 3 and 4. Summarizing these facts, we say that the IFBSA exhibits a reduction in the error, time and the number of iterations of the function as compared to the FBSA.
5 Applications
In this section, we illustrate the theoretical results which we have obtained in the previous section.
5.1 Split feasibility problems
Let \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\) be two real Hilbert spaces and \(\hbar : \mathcal{H}_{1} \rightarrow \mathcal{H}_{2}\) be a bounded linear operator. Let C and Q be closed, convex and nonempty subsets of \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. The split feasibility problem aims to find \(\bar{x} \in C\) such that \(S\bar{x} \in Q\). We represent the solution sets by \(\omega := C \cap \hbar ^{-1}(Q) = \{\bar{y} \in C: \hbar \bar{y} \in Q\}\). Censor and Elfving [7] introduced it to solve inverse problems and their application to medical image reconstruction and radiation therapy in a finite dimensional Hilbert space. For the set C, recall the function
The proximal operator of \(b_{C}\) is the metric projection on C,
Let \(P_{Q}\) be the projection of \(\mathcal{H}_{2}\) onto a nonempty, convex and closed subset Q. Take: \(f(\bar{x})=\frac{1}{2} \Vert \hbar \bar{x}-P_{Q}\hbar \bar{x} \Vert ^{2}\) and \(g(\bar{x})=b_{C}(\bar{x})\). Then we compute the split feasibility problem from the following result.
Corollary 5.1
Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two Hilbert spaces and let \(C \subseteq \mathcal{H}_{1}\) and \(Q \subseteq \mathcal{H}_{2}\) be nonempty, closed and convex subsets of Hilbert spaces \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. Assume that \(\Gamma =\omega \cap \Omega \cap \bigcap^{i=1}_{N}Fix(S_{i}) \neq \emptyset \) with hypotheses (H1)–(H4). Let \(\Theta _{k}\) be a bounded real sequence and \(m_{k} \in (0 , \frac{2}{ \Vert \hbar \Vert ^{2}})\). For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequences \((x_{k})\), \((b_{k})\), \((\ell _{k})\), \((w_{k})\), \((y_{k})\) and \((x_{k+1})\) be generated by
where \(J_{k}=P_{C}(Id-m_{k}\hbar ^{\ast }(I-P_{Q})\hbar )\). Assume that the conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (41) converges strongly to an element \(\bar{x}=P_{\Gamma }x_{1}\).
5.2 Monotone variational inequality problems
Let \(\mathcal{H}_{1}\) be a Hilbert space and C be a nonempty, closed and convex subset of \(\mathcal{H}_{1}\). Let \(\mathcal{B}:C \rightarrow \mathcal{H}_{1}\) be a nonlinear monotone operator. The variational inequality problem aims to find a point \(\bar{x} \in C\) such that
The solution set of the above problem is denoted by ω and assume that \(\omega \neq \emptyset \). [29], The resolvent operator acts as a projection operator \(P_{C}\). Then we compute monotone variational inequality problems from the following result.
Corollary 5.2
Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two Hilbert spaces and let \(C \subseteq \mathcal{H}_{1}\) and \(Q \subseteq \mathcal{H}_{2}\) be nonempty, closed and convex subsets of Hilbert spaces \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. Assume that \(\Gamma =\omega \cap \Omega \cap \bigcap^{i=1}_{N}Fix(S_{i}) \neq \emptyset \) with hypotheses (H1)–(H4). Let \(\Theta _{k}\) be a bounded real sequence and \(m_{k} \in (0 , \frac{2}{ \Vert \hbar \Vert ^{2}})\). For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequences \((x_{k})\), \((b_{k})\), \((\ell _{k})\), \((w_{k})\), \((y_{k})\) and \((x_{k+1})\) be generated by
where \(J_{k}=P_{C}(Id-m_{k}\mathcal{B})\). Assume that the conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (43) converges strongly to an element \(\bar{x}=P_{\Gamma }x_{1}\).
5.3 Convex minimization problems
Let \(f: \mathcal{H}_{1} \rightarrow \mathbb{R}\) and \(g: \mathcal{H}_{1} \rightarrow \mathbb{R}\) be two convex, proper and lower semicontinuous functions. In Algorithm 2, set that \(\mathcal{A} := \partial f\) and \(\mathcal{B} := \nabla g\). Assume that ω is the set of solutions of problem (4) and \(\omega \neq \emptyset \). Then we compute the convex minimization problem from the following result.
Corollary 5.3
Let \(\mathcal{H}_{1}\), \(\mathcal{H}_{2}\) be two Hilbert spaces and let \(C \subseteq \mathcal{H}_{1}\) and \(Q \subseteq \mathcal{H}_{2}\) be nonempty, closed and convex subsets of Hilbert spaces \(\mathcal{H}_{1}\) and \(\mathcal{H}_{2}\), respectively. Assume that \(\Gamma =\omega \cap \Omega \cap \bigcap^{i=1}_{N}Fix(S_{i}) \neq \emptyset \) with hypotheses (H1)–(H4). Let \(\Theta _{k}\) be a bounded real sequence and \(m_{k} \in (0,\frac{2}{ \Vert \hbar \Vert ^{2}})\). Let \(f , g:\mathcal{H}_{1} \rightarrow \mathbb{R}\) be two convex, proper and lower semicontinuous functions, such that f is sub-differential function and g is differentiable with γ-Lipschitz continuous gradient. For given \(x_{0},x_{1} \in \mathcal{H}_{1}\), let the iterative sequences \((x_{k})\), \((b_{k})\), \((\ell _{k})\), \((w_{k})\), \((y_{k})\) and \((x_{k+1})\) be generated by
where \(J_{k}=J^{\partial f}_{m_{k}}(Id-m_{k}\nabla g)\). Assume that the conditions (C1)–(C4) hold, then the sequence \((x_{k})\) generated by (44) converges strongly to an element \(\bar{x}=P_{\Gamma }x_{1}\).
6 Conclusions
In this paper, we have devised an inertially constructed forward–backward splitting algorithm for computing a common solution of the finite family of demicontractive operators, SEP and monotone inclusion problem in Hilbert spaces. The theoretical framework of the algorithm has been strengthened with an appropriate numerical example. Moreover, this framework has also been implemented to various instances of the monotone inclusion problems. We would like to emphasize that the above mentioned problems occur naturally in many applications, therefore, iterative algorithms are inevitable in this field of investigation. As a consequence, our theoretical framework constitutes an important topic of future research.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Alvarez, F.: Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert spaces. SIAM J. Optim. 14, 773–782 (2004)
Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A.: An inertial based forward–backward algorithm for monotone inclusion problems and split mixed equilibrium problems in Hilbert spaces. Adv. Differ. Equ. 2020, 453 (2020)
Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A., Sarwar, H., Din, H.F.: Approximation results for split equilibrium problems and fixed point problems of nonexpensive semigroup in Hilbert spaces. Adv. Differ. Equ. 2020, 512 (2020)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics. Springer, New York (2011)
Blum, E., Oettli, W.: From optimization and variational inequalities to equilibrium problems. Math. Stud. 63, 123–145 (1994)
Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)
Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projection in a product space. Numer. Algorithms 8, 221–239 (1994)
Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 21, 2071–2084 (2005)
Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59, 301–323 (2012)
Combettes, P.L.: The convex feasibility problem in image recovery. Adv. Imaging Electron Phys. 95, 155–453 (1996)
Combettes, P.L., Hirstoaga, S.A.: Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 6, 117–136 (2005)
Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)
Daniele, P., Giannessi, F., Mougeri, A.: Equilibrium Problems and Variational Models. Nonconvex Optimization and Its Application, vol. 68. Kluwer Academic, Dordrecht (2003)
Douglas, J., Rachford, H.H.: On the numerical solution of the heat conduction problem in two and three space variables. Trans. Am. Math. Soc. 82, 421–439 (1956)
Hicks, T.L., Kubicek, J.D.: On the Mann iteration process in a Hilbert space. J. Math. Anal. Appl. 59, 498–504 (1977)
Khan, A., Abdeljawad, T., Gomez-Aguilar, J.F., Khan, H.: Dynamical study of fractional order mutualism parasitism food web module. Chaos Solitons Fractals 134, Article ID 109685 (2020)
Khan, A., Gomez-Aguilar, J.F., Abdeljawad, T., Khan, H.: Stability and numerical simulation of a fractional order plant-nectar-pollinator model. Alex. Eng. J. 59(1), 49–59 (2020)
Khan, A., Syam, M.I., Zada, A., Khan, H.: Stability analysis of nonlinear fractional differential equations with Caputo and Riemann–Liouville derivatives. Eur. Phys. J. Plus 133, 264 (2018)
Khan, H., Gomez-Aguilar, J.F., Alkhazzan, A., Khan, A.: A fractional order HIV-TB coinfection model with nonsingular Mittag-Leffler law. Math. Methods Appl. Sci. 43(6), 3786–3806 (2020)
Khan, H., Khan, A., Jarad, F., Shah, A.: Existence and data dependence theorems for solutions of an ABC-fractional order impulsive system. Chaos Solitons Fractals 131, Article ID 109477 (2020)
Khan, M.A.A.: Convergence characteristics of a shrinking projection algorithm in the sense of Mosco for split equilibrium problem and fixed point problem in Hilbert spaces. Linear Nonlinear Anal. 3, 423–435 (2017)
Khan, M.A.A., Arfat, Y., Butt, A.R.: A shrinking projection approach to solve split equilibrium problems and fixed point problems in Hilbert spaces. UPB Sci. Bull., Ser. A 80(1), 33–46 (2018)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)
Lopez, G., Martin-Marquez, V., Wang, F., Xu, H.K.: Forward–backward splitting methods for accretive operators in Banach spaces. Abstr. Appl. Anal. 2012, Article ID 109236 (2012)
Martinez-Yanes, C., Xu, H.K.: Strong convergence of CQ method for fixed point iteration processes. Nonlinear Anal. 64, 2400–2411 (2006)
Moudafi, A.: Split monotone variational inclusions. J. Optim. Theory Appl. 150, 275–283 (2011)
Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(\frac{1}{k^{2}})\). Dokl. Akad. Nauk SSSR 269, 543–547 (1983)
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4(5), 1–17 (1964)
Rockafellar, R.T.: On the maximality of sums of nonlinear monotone operators. Trans. Am. Math. Soc. 149, 75–88 (1970)
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14, 877–898 (1976)
Suantai, S.: Weak and strong convergence criteria of Noor iterations for asymptotically nonexpansive mappings. J. Math. Anal. Appl. 311, 506–517 (2005)
Takahashi, W., Xu, H.K., Yao, J.C.: Iterative methods for generalized split feasibility problems in Hilbert spaces. Set-Valued Var. Anal. 23, 205–221 (2015)
Tseng, P.: Applications of a splitting algorithm to decomposition in convex programming and variational inequalities. SIAM J. Control Optim. 29, 119–138 (1991)
Acknowledgements
The authors wish to thank the anonymous referees for their comments and suggestions. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research was supported by Research Center in Mathematics and Applied Mathematics, Chiang Mai University.
Funding
This research was supported by Chiang Mai University. The author Yasir Arfat was supported by the Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi, Thailand (Grant No.16/2562).
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arfat, Y., Kumam, P., Khan, M.A.A. et al. An inertially constructed forward–backward splitting algorithm in Hilbert spaces. Adv Differ Equ 2021, 124 (2021). https://doi.org/10.1186/s13662-021-03277-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03277-0
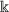 -demicontractive if
-demicontractive if 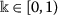 such that
such that 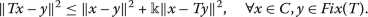
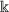 -demicontractive operators;
-demicontractive operators; ;
;




